文档内容
2024-2025 学年江苏省盐城市七校联盟高二下学期 4 月期中联考
数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知随机变量 的分布规律为 ,则 ( )
2
= = ( =1,2,3) =3 =
A. B. C. D.
9 1 2 1
2.若14 ,则3 ( ) 7 14
2 +1 ∗
A. 13 = 13 ∈ B. 6 = C. D.
3.30 的展开式中 的系12数0为( ) 360 720
4 3
A. − B. C. D.
4.已6知 为平面 的一个法向量−4, 为直线 的一个方4 向向量,则“ ”−是6 “ ”的( )
A.充分� �不必要条 件 � � B.必要不充分条件 // � �⊥� �
C.充要条件 D.既不充分也不必要条件
5.已知随机变量 的取值为 , , ,若 , ,则标准差为( )
1
0 1 2 =0 =5 =1
A. B. C. D.
2 3 10 2 5
6.从5 红、黄、蓝、黑 种不同5 的颜色中选出一些颜5色给如图所示的 个5格子涂色,每个格子涂一种颜色,
记事件 为“相邻的 4个格子颜色不同”,事件 为“ 个格子的颜色3 均不相同”,则 ( )
2 3 ( | )=
A. B. C. D.
1 1 1 2
4 2 3 3
7.已知正四棱锥 的所有棱长均为 , 为底面 内一点,且 ,
1 1
则 ( )
− 1 ��� ��=3 ��� ��+ ��� ��+2 ��� � ∈
��� ��⋅ ��� ��=
A. B. C. D.
5 7 3 4
8.若12 12 ,则4 下列说法错误的是(3 )
10 2 10
A. 3− = 0+ 1 + 2 +⋯+ 10
10
B. 0 =3
10
C. 0 + 1的+展 开2式+中⋯偶+数 项9的+二 项10式=系4数之和为
10 9
D. 3− 的展开式中二项式系数最大项为 2
10 5 5 5
二、3多−选 题:本题共3小题,共18分。在每 小10题⋅3给出⋅ 的选项中,有多项符合题目要求。
第 页,共 页
1 89.将一个量用两种方法分别算一次,由结果相同得到等式,在数学中将这种思想方法称为“算两次”请用
此法判断下列等式中,正确的有( ) .
A. B.
−1 +1
C. +1 = + D. +1 = +1
−1 −1
10. 在 某+独 立 重复=实 验+1中,事件 相互独立,且在 一 次=实 验 中−1,事件 发生的概率为 ,事件 发生的概率
为 ,其中 若进行 ,次 实验,记事件 发生的次数为 ,事 件 发生的次数 为 ,事 件 发生的
次数1为− ,则下 列∈结(论0,1正).确的是( )
A. B.
= 1− =
C. D.
2
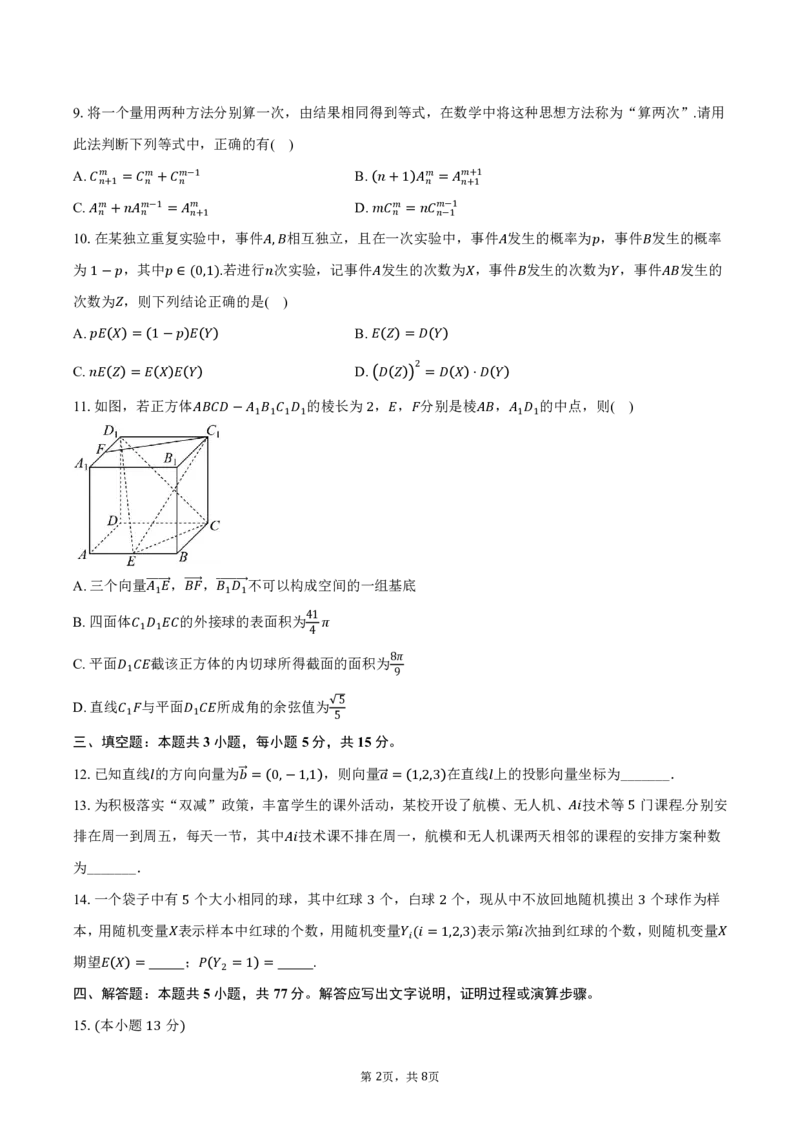
11. 如 图 ,=若 正 方 体 的棱长为 , , 分=别 是 棱⋅ , 的中点,则( )
− 1 1 1 1 2 1 1
A.三个向量 , , 不可以构成空间的一组基底
B.四面体 ���1� �� 的 ��� 外 �� 接 �� 球 �1� � 的 ��1� 表面积为
41
1 1 4
C.平面 截该正方体的内切球所得截面的面积为
8
1 9
D.直线 与平面 所成角的余弦值为
5
三、填空 1 题 :本题 共 1 3 小题,每小题5分,5共15分。
12.已知直线 的方向向量为 ,则向量 在直线 上的投影向量坐标为_______.
13.为积极落实 “双减”政策� �,=丰0富,−学1生,1的课外活动� �,=某1校,2,开3设了航模 、无人机、 技术等 门课程分别安
排在周一到周五,每天一节,其中 技术课不排在周一,航模和无人机课两天相邻 的课程的5安排方案. 种数
为_______.
14.一个袋子中有 个大小相同的球,其中红球 个,白球 个,现从中不放回地随机摸出 个球作为样
本,用随机变量 表5示样本中红球的个数,用随机3变量 2 表示第 次抽到红球的个数,3则随机变量
期望 ; ( =1,2,3)
四、解 答 题=:本题共 5 小2题=,1共=77分。.解答应写出文字说明,证明过程或演算步骤。
15. 本小题 分
( 13 )
第 页,共 页
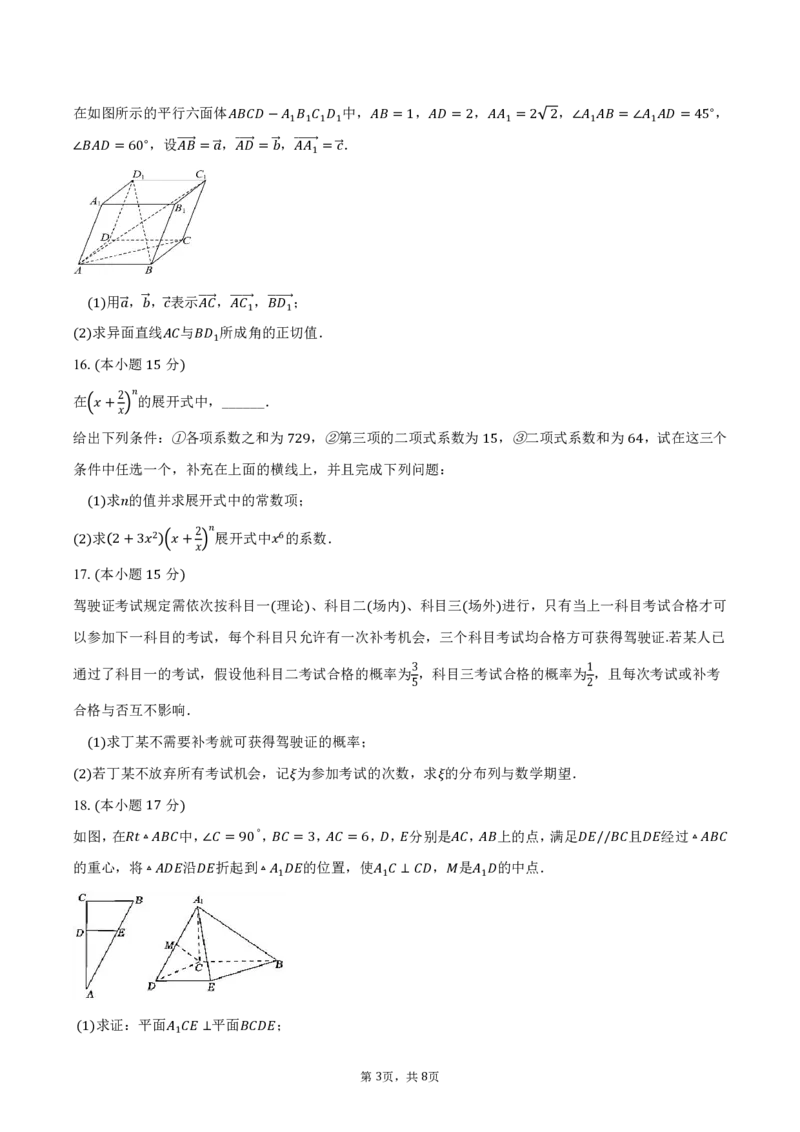
2 8在如图所示的平行六面体 中, , , , ,
∘
,设 , −, 1 1 1 1. =1 =2 1 =2 2 ∠ 1 = ∠ 1 =45
∘
∠ =60 ��� ��=� � ��� ��=� � ��� ��1�=� �
用 , , 表示 , , ;
(求1)异�面 � 直� �线� � 与 ��� �所 �成�� ��角1� 的 ��正� ��1�切值.
(126). 本小题 分 1
( 15 )
在 的展开式中,______.
2
给出 下+列 条件:①各项系数之和为 ,②第三项的二项式系数为 ,③二项式系数和为 ,试在这三个
条件中任选一个,补充在上面的横线72上9,并且完成下列问题: 15 64
求 的值并求展开式中的常数项;
(1)
求 展开式中 的系数.
2 2 6
( 1 2 7 ). 本2小+题3 分 +
驾驶(证考试规15定需)依次按科目一 理论 、科目二 场内 、科目三 场外 进行,只有当上一科目考试合格才可
以参加下一科目的考试,每个科目( 只允)许有一次(补考机) 会,三个(科目考) 试均合格方可获得驾驶证若某人已
.
通过了科目一的考试,假设他科目二考试合格的概率为 ,科目三考试合格的概率为 ,且每次考试或补考
3 1
合格与否互不影响. 5 2
求丁某不需要补考就可获得驾驶证的概率;
(若1)丁某不放弃所有考试机会,记 为参加考试的次数,求 的分布列与数学期望.
(128). 本小题 分
如图(,在 17 中) , , , , , 分别是 , 上的点,满足 且 经过
∘
的重心, 将 ▵ 沿 ∠ 折=起9到0 =的3位 置 ,=使6 , 是 的中点. // ▵
▵ ▵ 1 1 ⊥ 1
求证:平面 平面 ;
(1) 1 ⊥
第 页,共 页
3 8求 与平面 所成角的大小;
(2) 1
在线段 上是否存在点 不包含端点 ,使平面 与平面 夹角正切值为 ?若存在,求出
39
的(3长) 度;若 不 1 存在,请说明理 由( . ) 3 1
19. 本小题 分
设函(数 17 ) .
( , )= 1+ ( >0)
若 且 ,求 ;
1 2 3 3
(1) 当 (3, )= 时 , 0+ 求 + 2 展 + 开 3 式 中 2 系 = 数 27 最大的 � 项 =0 ;
(2)当 =−时3 ,设 是 正(6,整 )数,为正实数,实数 满足 ,求证:
(3) .>0 ( ,1)= ( , ) (2025,1000 )>7 (−
2025, )
第 页,共 页
4 8参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10 .
11.
12.
1 1
13.
(0,−2,2)
14.
36;
9 3
15.5解:5 ,
(1) ��� ��1�=�, �+� �+� � ,
��� ��1因�=为−� �+� �+� � ��� �=,� �+� � ,
(同2)理可求 ���得 ��1�=� �+� �−� � , ��� �=� �+� �,
又因为 | ��� ��1�|= 15 | ��� �|= 7
��� ��1�· ��� �=(� �+� �−� �),·(� �+� �)
2 2
=所 � 以 � −� � +� �·� �+� �·� �=9 ,
�������������
1· 9 3 105
cos ��� ��1�, ��� � = | ��� ���� 1 � || ��� �� | = 15× 7= 35
所以 ,
2 70
sin ��� ��1�, ��� � = 35
所以
2 6
tan ��� ��1�, ��� � = 9
16.解: 在 的展开式中,
2
选条件①(1时),(各 +项 系)数之和为 ,令 ,故 ,解得 ,常数项为 .
3 3
选条件②时,第三项的二项式系72数9为 ,=故1 3 =,7解29得 , =常6数项为 6⋅2 =.160
2 3 3
选条件③时,由于二项式系数和为 1,5所以 =15,所以 =6,常数项为 6⋅2 =160.
3 3
64 2 =64 =6 6⋅2 =160
第 页,共 页
5 8由上可知不论选 ① ② ③,都有 ,则问题为求 展开式中 的系数,
2 2 6
(2) =6 (2+3 )( + )
先求 展开式中含 的项,易知该项为 ,
2 6 6 0 6 −1 0 6
( + ) 6 (2 ) =
再求 展开式中含 的项,易知该项为 ,
2 6 4 1 5 −1 1 4
( + ) 6 (2 ) =12
所以 展开式中含 的项为 ,
2 2 6 6 6 6
所以其 (2 系 + 数 3 为 )( + . ) 2 +3×12 =38
17.解:设“科3目8二第一次考试合格”为事件 “科目二补考考试合格”为事件 ,
“科目三第一次考试合格”为事件 “科目三 1补; 考考试合格”为事件 2
则 、 、 、 相互独立. 1; 2;
1 2 1 2
他不需要补考就可获得驾证的概率为: .
3 1 3
(1) = ( 1⋅ 1)= ( 1)⋅ ( 1)= 5×2=10
即丁某不需要补考就可获得驾驶证的概率为 .
3
的可能取值为 , , . 10
(2) 2 3 4
,
3 1 2 2 23
∵ ( =2)= ( 1 1+ 1 2)= 5×2+5×5=50
,
3 1 2 3 1 21
( =3)= ( 1 1+ 1 2 1)= 5×2+5×5×2=50
.
2 3 1 3
=的(分 =布4列)为= ( 1 2 1)= 5×5×2=25
∴
2 3 4
23 21 3
50 50 25 .
23 21 3 133
( )=2×50+3×50+4×25= 50
即丁某不放弃所有考试机会的数学期望为
133
18. 证明:因为在 中, 50,所以 ,又 ,所以 , ,
∘
则折(1叠)后 , 又 △ ∠ ,=90 , 平 面⊥ , 所 以// 平面 ⊥, ⊥ 1
平面 ⊥ ,1 所以 1 ∩ ,=又 已知 1 ⊂, 1 , 且 ⊥ , 都1 在 面 内,
所1以 ⊂ 平 1面 , 又 ⊥ 1 平面 , 1所 以⊥ 平 面 ∩ 平 面=
由 1 ,⊥分别 以 , ,1 ⊂所在 直1 线 为 轴, 轴, 1 轴 ,⊥建立 空 间 直; 角坐标系 ,
(2) (1) 1 −
第 页,共 页
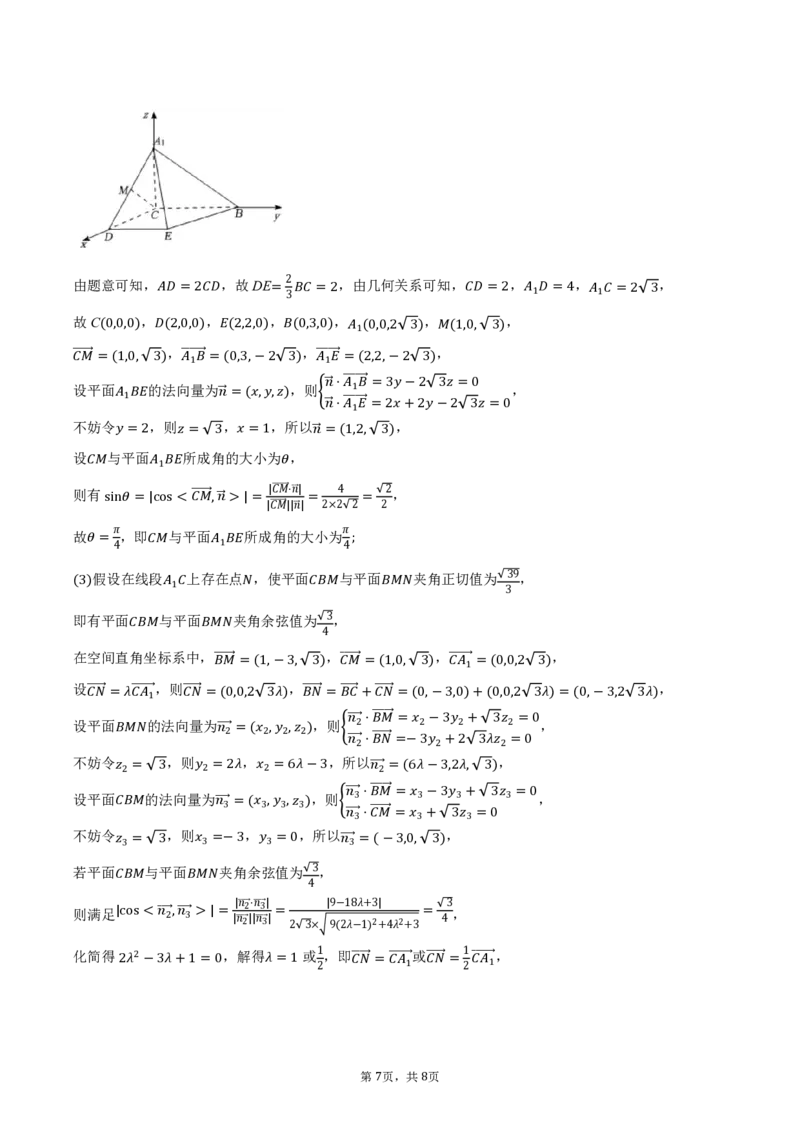
6 8由题意可知, ,故DE ,由几何关系可知, , , ,
2
故C , =2 , ,=3 =2, , =2 , 1 =4 1 =2 3
(0,0,0) (,2,0,0) (2,2,0) (0,,3,0) 1(0,0,2 3) , (1,0, 3)
� 设 �� � 平 �=面(1,0, 的3)法向 ���1 量 � �� 为=(0,3,−2 3,)则 ���1� ��=(2,2,−2 3) ,
� �⋅ ���1� ��=3 −2 3 =0
不妨令 1 ,则 � �,=( , ,, )所以 ,
� �⋅ ���1� ��=2 +2 −2 3 =0
设 与 平=面2 所=成角3的 大=小1为 , � �=(1,2, 3)
1
则有 ,
| ��� ��� ⋅� �| 4 2
sin =|cos < ��� ��,� �>|= | ��� ��� ||� �| =2×2 2= 2
故 ,即 与平面 所成角的大小为
= 4 1 4;
假设在线段 上存在点 ,使平面 与平面 夹角正切值为 ,
39
(3) 1
3
即有平面 与平面 夹角余弦值为 ,
3
在空间直角坐标系中, 4, , ,
设 ,则 ��� ��=(1,−3,, 3) ��� ��=(1,0, 3) ��� ��1�=(0,0,2 3) ,
设平 ��� �� 面= ��� �� 的 1� 法向 �� 量 � �� 为=(0,0,2 3 ) ��� , ��=则 ��� ��+ ��� ��=(0,−3,0)+(0,0,2 3, )=(0,−3,2 3 )
���2�⋅ ��� ��= 2−3 2+ 3 2 =0
不妨令 ,则 ���2�=,( 2, 2, 2) ,所以 ,
���2�⋅ ��� ��=−3 2+2 3 2 =0
设平面 2 =的法3 向量 为 2 =2 2 =6 − , 3 则 ���2�=(6 −3,2 , 3) ,
���3�⋅ ��� ��= 3−3 3+ 3 3 =0
不妨令 ,则 ���3�=,( 3, 3, , 3)所以 ,
���3�⋅ ��� ��= 3+ 3 3 =0
若平面 3 =与平3 面 3 = 夹 − 角 3 余 弦 3 值 = 为 0 , ���3�=(−3,0, 3)
3
4
则满足 ,
| ���2�⋅ ���3�| |9−18 +3| 3
|cos< ���2�, ���3�>|= | ���2�|| ���3�|= 2 2 = 4
2 3× 9(2 −1) +4 +3
化简得 ,解得 或 ,即 或 ,
2 1 1
2 −3 +1=0 =1 2 ��� ��= ��� ��1� ��� ��=2 ��� ��1�
第 页,共 页
7 8又点 不包含 端点,所以 ,即 .
1
1 ��� ��=2 ��� ��1� 1 = 3
故在线段 上存在这样的点 ,使平面 与平面 夹角正切值为 ,此时 的长度为 .
39
19.解: 1 , 3 , 1 3
1 2 3 3 2 2
(1) (3, )= 0+ + 2+ 3 =(1+ ) 2 = 3 =27 ⇒ =±3
所以 ,
3
( , )=(1± ) ( >0)
当 时,
3 3 3
∴ =3 � =0 =(1+1) =64;
当 时, .
3 3 3
=−3 � =0 =(1−1) =−8
由条件得, ,
3 6
(2) (6, )=(1− )
所以 , , , , , , , .
−3 −
由于要 + 求 1 展 = 开 6 式 ( 中 系 ) 数 = 最 6 大 (− 的 3 项 ) , 所以 为 = 偶 0 数 1 , 2 3 4 5 6
由题意知,展开式中系数最大的项应当 在第 项或第 项中出现,
∴ , ,3 5
2 −3 2 135 4 −3 4 1215
3 = 6( ) = 2 5 = 6( ) = 4
展开式中系数最大的项是第 项且为 .
1215
∴ 5 4
由 可得 ,
2
(3) ( ,1)= ( , ) (1+ ) = (1+ ) =( + )
即
2
2025 1 2025
1+ = + ⇒ = ⇒ (2025,1000 )=(1+1000 ) =(1+1000)
,
1 1 2 1 2 3 1 3 4 1 4 4 2
>1+ 2055 1000+ 2055(1000) + 2055(1000) + 2055(1000) >1+2+2+3+3=7
而 ,
−2025 1 −2025
所以 ( 原 − 不 20 等 25 式 , )=(1+ ) =(1+ ) 成 < 立 1 .
(2025,1000 )>7 (−2025, )
第 页,共 页
8 8