文档内容
宁夏育才中学 2 0 2 6 届高三年级第一次月考数学答案
选择题答案
题号 1 2 3 4 5 6 7 8 9 10 11
答案 A A B B C B B A AB AD ABD
填空题答案
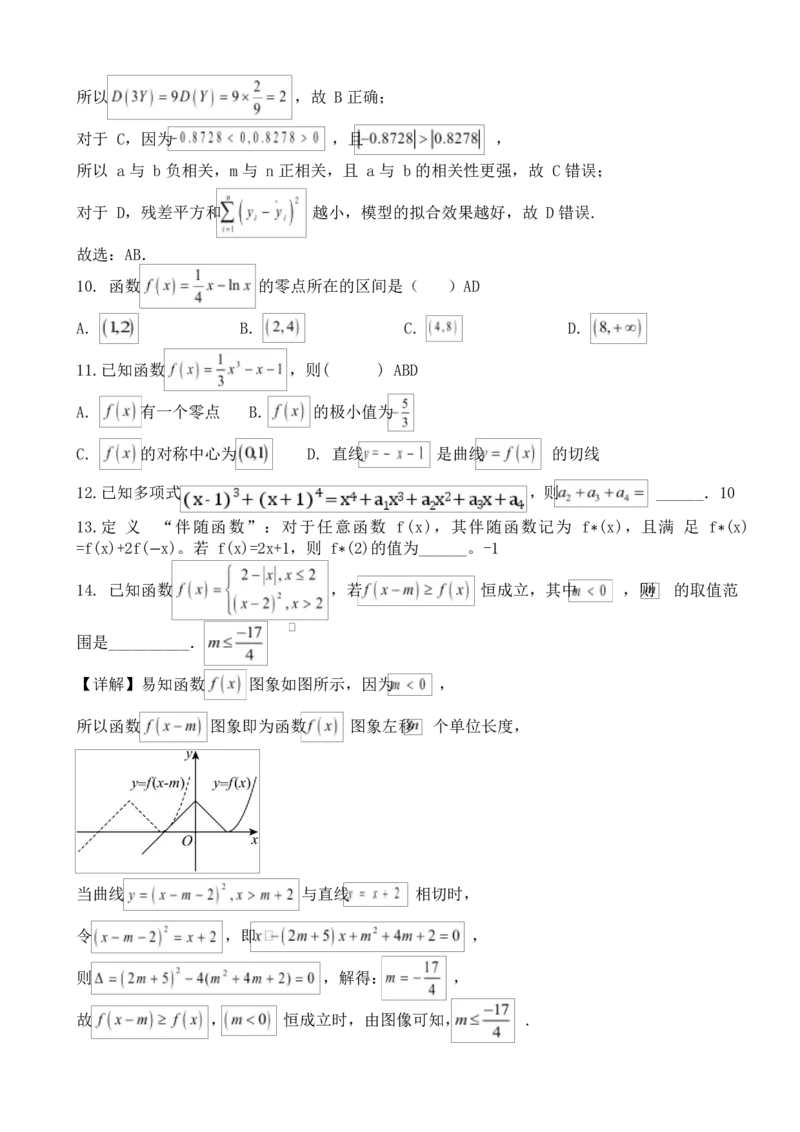
12.10;13. -1;14.
1.已知集合 则 A∪B= ( )
2.p:角α的终边过点 P(1,2),q:sin α=5)5,则 p 是 q 的( )A
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
答案: A 若角α的终边经过点 P(1,2),则 sin α=2\r(12+22)=5)5,故充分性成立;
若 sin α=5)5,设角α的终边上一点为 P(x,y),则 y\r(x2+y2)=5)5=2\r(5),不妨设
y =2t>0,则 x2+y2=5t2,解得 x=t,y=2t)或 x=-t,y=2t.)显然当 x=-t,y=2t)
时, 角α的终边不过点 P(1,2),故必要性不成立.综上,p 是 q 的充分不必要条件.
3.设 a 则 a, b, c 的大小关系是( ) . B
A. b0 时,g(x)=f(x)+x2。
(1) 求 g(1) 和 g( 1) 的值;
(2) 求函数 g(−x) 在 x<0 时的解析式。 答案:(1)g(1)=2,
g( 1)= 2(2)当 −x<0 时,g(x)= x2+2x+1
16.已知函数 处取得极值.
− − −
(1)求函数 的单调区间;
(2)求函数 在区间 上的最大值与最小值.
【答案】(1)单调递增区间为 , ,单调递减区间为 .
(2)最大值为 2,最小值为 .
17.2025 年 4 月,中国新能源汽车零售渗透率突破 ,进入“以电为主”的新阶段,充电
桩的使用率也成为关注焦点.经调查,某市今年 月份的充电桩日均使用时长 (时)与
新能源汽车保有量 (万辆)及充电桩日均使用率 ( ,为常数)的数据如下表所
示:
月份 1 2 3 4 5 6
新能源汽车保有量 (万辆) 8 13 15 18 23 25
充电桩日均使用时长 (时) 5 7 10 12 15 17
充电桩日均使用率 0.15 0.21 0.3 0.36 0.45 0.51
(1)若用充电桩日均使用率近似估计一个充电桩一天内被使用的概率,设该市某个充电桩在
3 月份的某 3 天中被使用的天数为 ,求 的分布列;
(2)求 关于 的样本相关系数,并说明线性相关程度的强弱;(精确到 0.01)
(3)若 关于 的经验回归方程为 ,求 的值(精确到 0.1),并预测当该市某月
的新能源汽车保有量为 36 万辆时,充电桩的日均使用率为多少.
参考数据: , .
参考公式:相关系数 .
答案:【小问 1 详解】
由题可知 的所有可能取值为 ,且 ,则 ,
,
,
,
所以 的分布列为
0 1 2 3
0.343 0.441 0.189 0.027
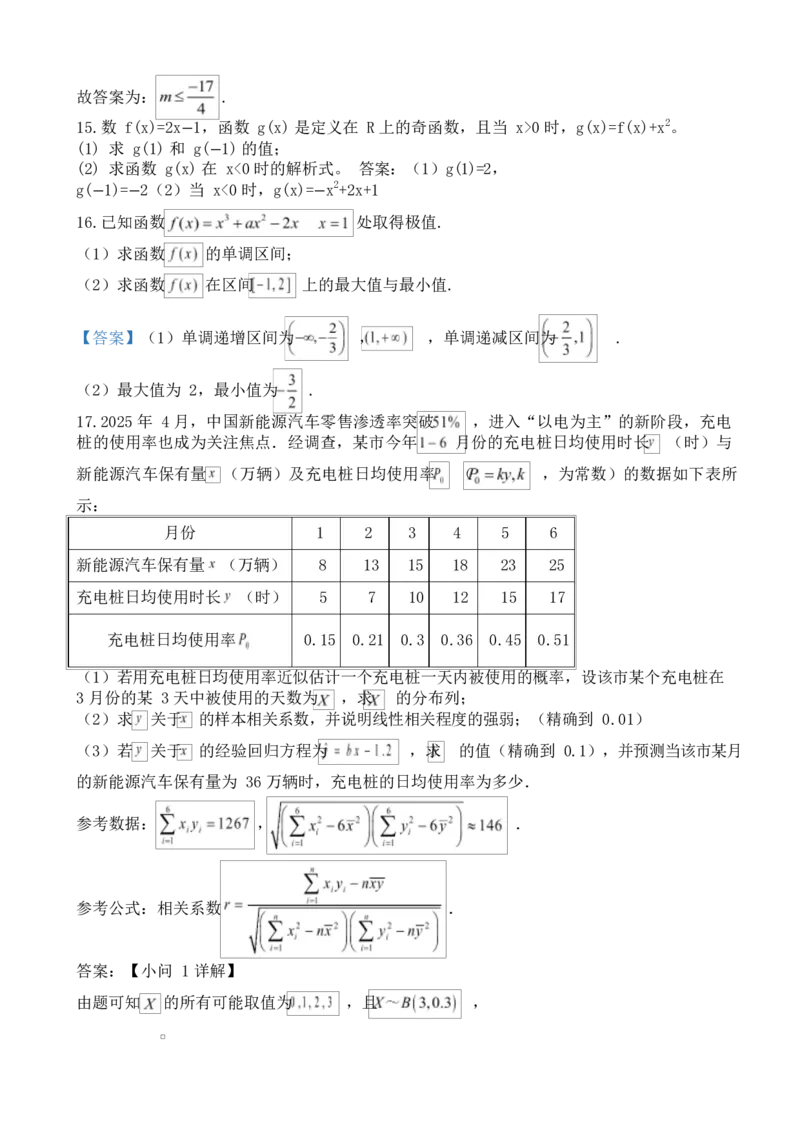
【小问 2 详解】由题可知 , ,
则 ,
因为 接近于 1,所以 与 的线性相关程度较强.
【小问 3 详解】
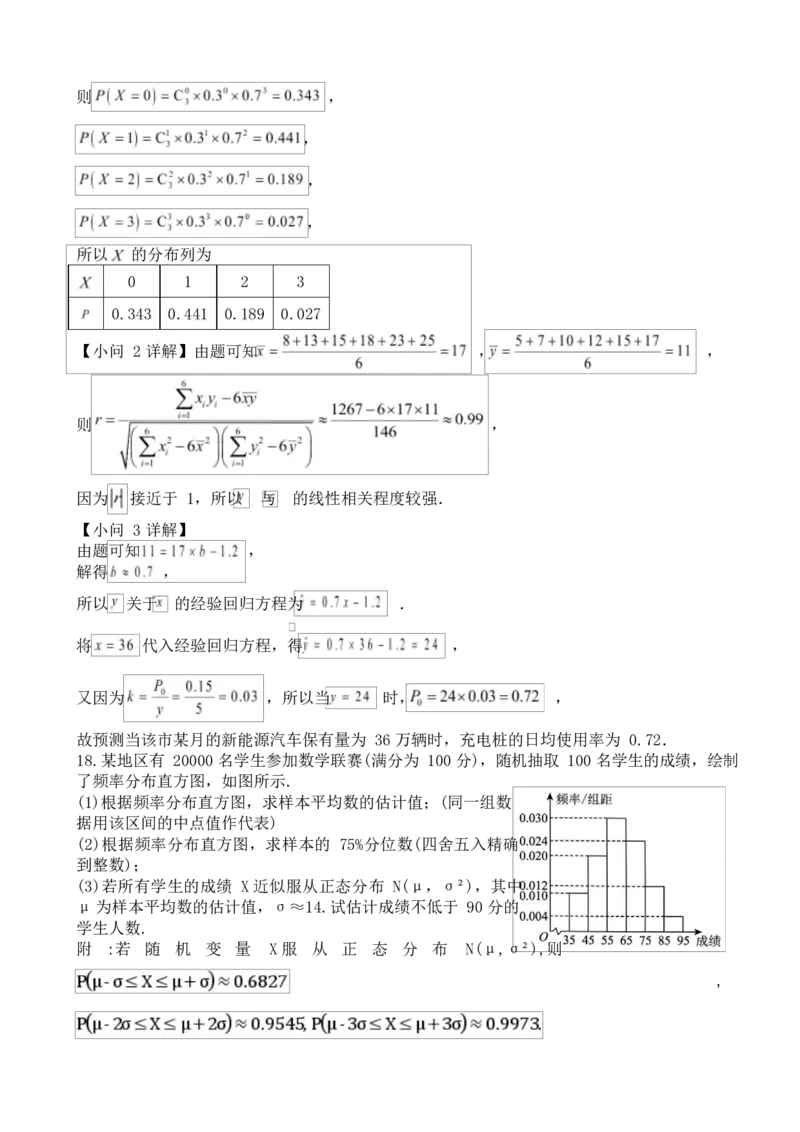
由题可知 ,
解得 ,
所以 关于 的经验回归方程为 .
将 代入经验回归方程,得 ,
又因为 ,所以当 时, ,
故预测当该市某月的新能源汽车保有量为 36 万辆时,充电桩的日均使用率为 0.72.
18.某地区有 20000 名学生参加数学联赛(满分为 100 分),随机抽取 100 名学生的成绩,绘制
了频率分布直方图,如图所示.
(1)根据频率分布直方图,求样本平均数的估计值;(同一组数
据用该区间的中点值作代表)
(2)根据频率分布直方图,求样本的 75%分位数(四舍五入精确
到整数);
(3)若所有学生的成绩 X 近似服从正态分布 N(μ,σ²),其中
μ为样本平均数的估计值,σ≈14.试估计成绩不低于 90 分的
学生人数.
附 :若 随 机 变 量 X 服 从 正 态 分 布 N(μ,σ²),则
,19.已知函数 .
(1)求曲线 在点 处的切线方程;(2)求 的单调区间;(3)证明:
.
答 案 : ( 1) ,
,
故曲线 在点 处的切线方程为 ,
即曲线 在点 处的切线方程为 .
(2)设 ,
当 时, 单调递减;当 时, , 单调递增.
于是 ,故 , 在 上单调递增.
故 的单调递增区间为 , ,无单调递减区间.(3)设函数 .
当 时, 单调递减;当 时, 单调递增.
于是 .对于 ,有 ,即 .
当 时, ,即 ,此时 .
当 时, ,即 ,此时 .综上, .