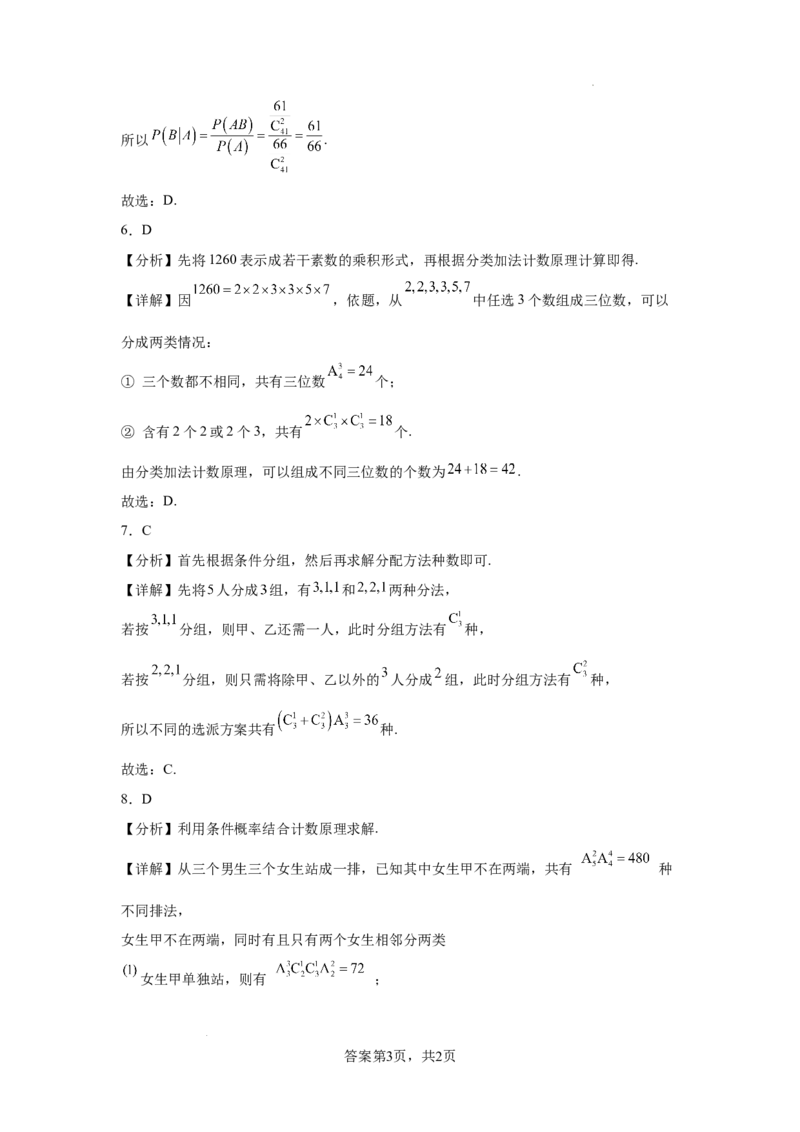
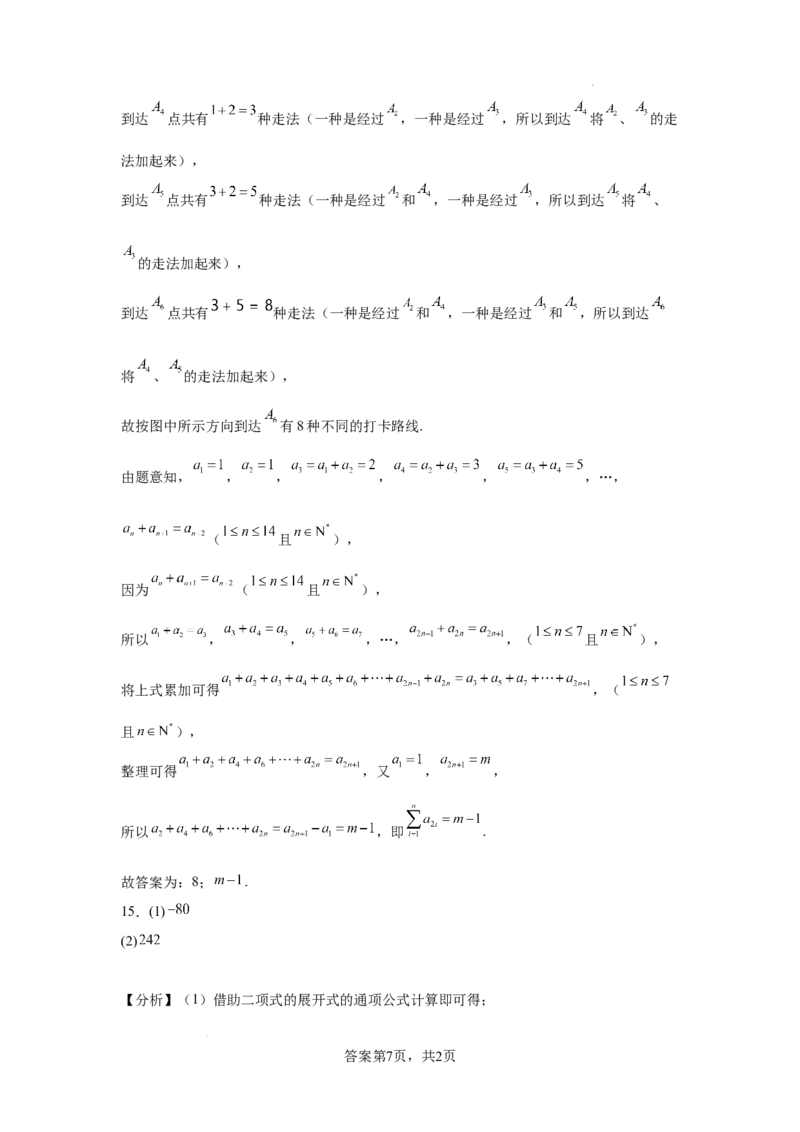文档内容
参考答案:
1.B
【分析】根据正态曲线的性质计算可得.
【详解】因为 ,又 ,
所以 ,
所以 .
故选:B.
2.D
【分析】由散点图判断A,根据回归直线方程判断B,求出 , ,根据回归直线方程必过
样本中心点求出 ,令 求出 ,即可判断D.
【详解】由散点图可知,商品的价格和需求量存在负相关关系,故A错误;
由经验回归方程为 ,可知 与 具有线性相关关系,故A错误;
又 , ,
又经验回归直线方程 必过样本中心点 ,
则 ,解得 ,故C错误;
当 时, ,
所以价格定为 万元,预测需求量大约为 ,故D正确.
故选:D.
3.A
【分析】由分类、分步计数原理结合组合数即可运算求解.
【详解】若要产生 这一项,则
当在 中取1时,再在 中取2个 、取4个1,
答案第1页,共2页
学科网(北京)股份有限公司当在 中取 时,再在 中取3个 、取3个1,
所以 展开式中 的系数为 .
故选:A.
4.A
【分析】设事件 :抽到的是次品,事件 :抽到的配件来自A制造厂,事件 :抽到
的配件来自 制造厂,事件 :抽到的配件来自 制造厂,利用全概率公式计算可得.
【详解】设事件 :抽到的是次品,
事件 :抽到的配件来自A制造厂,事件 :抽到的配件来自 制造厂,事件 :抽到的
配件来自 制造厂,
由题意可知:
,
所以
.
故选:A.
5.D
【分析】分析可知自然数有41个,素数有12个,孪生素数有5组,根据条件概率公式结
合古典概型分析求解.
【详解】不超过 的自然数有41个,其中素数有 ,共12
个,
孪生素数有 和 , 和 , 和 , 和 ,29和31,共5组.
所以 , ,
答案第2页,共2页所以 .
故选:D.
6.D
【分析】先将1260表示成若干素数的乘积形式,再根据分类加法计数原理计算即得.
【详解】因 ,依题,从 中任选3个数组成三位数,可以
分成两类情况:
① 三个数都不相同,共有三位数 个;
② 含有2个2或2个3,共有 个.
由分类加法计数原理,可以组成不同三位数的个数为 .
故选:D.
7.C
【分析】首先根据条件分组,然后再求解分配方法种数即可.
【详解】先将 人分成 组,有 和 两种分法,
若按 分组,则甲、乙还需一人,此时分组方法有 种,
若按 分组,则只需将除甲、乙以外的 人分成 组,此时分组方法有 种,
所以不同的选派方案共有 种.
故选:C.
8.D
【分析】利用条件概率结合计数原理求解.
【详解】从三个男生三个女生站成一排,已知其中女生甲不在两端,共有 种
不同排法,
女生甲不在两端,同时有且只有两个女生相邻分两类
女生甲单独站,则有 ;
答案第3页,共2页
学科网(北京)股份有限公司女生甲和另一个女生站一起,则有 ,
所以,已知其中女生甲不在两端,则有且只有两个女生相邻的概率是 .
故选:D.
9.ABD
【分析】借助方差的性质、样本点中心的性质、线性相关系数的性质与残差的性质逐项判
断即可得.
【详解】对A:由方差的性质可知,将一组数据的每一个数减去同一个数后,
新数据的方差与原数据方差相同,故A正确;
对B:由 ,故线性回归直线 一定过样本点中心 ,故B正确;
对C:线性相关系数 越大,两个变量的线性相关性越强,故C错误;
对D:在残差的散点图中,残差分布的水平带状区域的宽度越窄,
其模型的拟合效果越好,故D正确.
故选:ABD.
10.ABD
【分析】由二项展开式中二项式系数之和为64求出 ,再得出通项,令 可得A正
确;由组合数的性质可得B正确;令 为整数,可得C错误;令 ,可得D正确;
【详解】因为 的二项展开式中二项式系数之和为64,
所以 ,所以二项式为 ,
通项为 ,
A:令 ,可得二项展开式中各项系数之和为 ,故A正确;
B:当 时,二项式系数 最大,即第四项,故B正确;
答案第4页,共2页C:令 为整数,解得 ,所以有4个有理项,故C错误;
D:因为通项为 ,
所以项的系数为 , ,
经检验, 时,项的系数最大,为 ,故D正确;
故选:ABD.
11.ABD
【分析】根据杨辉三角读出数据即可判断A,利用组合数公式判断B,分析各行数据的特
征,即可判断C,求出第 行中从左到右第 个数与第 个数,即可判断D.
【详解】对于A:第 行,第 行,第 行的第 个数字分别为: , , ,其和为
;
而第 行第 个数字就是 ,故A正确;
对于B:因为 , ,
所以 ,故B正确;
对于C:由图可知:第 行有 个数字,
如果 是偶数,则第 (最中间的)个数字最大;
如果 是奇数,则第 和第 个数字最大,并且这两个数字一样大,
所以第 行的第 个数最大,故C错误;
对于D:依题意:第 行从左到右第 个数为 ,第 行从左到右第 个数为
,
所以第 行中从左到右第 个数与第 个数之比为 ,故D正确;
故答案为:ABD.
12.
【分析】求得二项展开式的通项,结合通项求得 的值,代入列出方程,即可求解.
答案第5页,共2页
学科网(北京)股份有限公司【详解】由二项式 展开式的通项为 ,
令 ,可得 ,代入可得 ,解得 .
故答案为: .
13.420
【分析】利用分类计数原理求解,按2与4两区域种植果树是否相同进行分类即可.
【详解】分两类情况:
第一类:2与4种同一种果树,
第一步种1区域,有5种方法;
第二步种2与4区域,有4种方法;
第三步种3区域,有3种方法;
最后一步种5区域,有3种方法,
由分步计数原理共有 种方法;
第二类:2与4种不同果树,
第一步在1234四个区域,从5种不同的果树中选出4种果树种上,
是排列问题,共有 种方法;
第二步种5号区域,有2种方法,
由分步计数原理共有 种方法.
再由分类计数原理,共有 种不同的方法.
故答案为:420.
14. 8
【分析】结合题意及分类加法原理,依次计算到达 、 、 、 、 的走法即可.由题
意可知数列 为斐波那契数列,即 ( 且 ),结合累加法求
解即可.
【详解】由题意知,到达 点共有1种走法,
到达 点共有 种走法(一种是经过 点到达 ,一种是直接到达 ),
答案第6页,共2页到达 点共有 种走法(一种是经过 ,一种是经过 ,所以到达 将 、 的走
法加起来),
到达 点共有 种走法(一种是经过 和 ,一种是经过 ,所以到达 将 、
的走法加起来),
到达 点共有 种走法(一种是经过 和 ,一种是经过 和 ,所以到达
将 、 的走法加起来),
故按图中所示方向到达 有8种不同的打卡路线.
由题意知, , , , , ,…,
( 且 ),
因为 ( 且 ),
所以 , , ,…, ,( 且 ),
将上式累加可得 ,(
且 ),
整理可得 ,又 , ,
所以 ,即 .
故答案为:8; .
15.(1)
(2)
【分析】(1)借助二项式的展开式的通项公式计算即可得;
答案第7页,共2页
学科网(北京)股份有限公司(2)借助二项式的展开式的通项公式可去绝对值,再借助赋值法,分别令 及 计
算即可得.
【详解】(1)对 ,有 ,
则有 ,
即 ; 6分
(2)由 ,则 , ,
故 ,
令 ,可得 ,即 ,
令 ,有 ,
即 ,
即 . 13分
16.(1)填表见解析;认为对“数学建模”选修课的兴趣度与性别无关
(2)分布列见解析;期望为
【分析】(1)根据题意,完成 列联表,计算 值并根据其与 的比较得出结论;
(2)由题意,可分析得出变量 服从超几何分布,按照其概率公式写出分布列,计算数
学期望即得.
【详解】(1) 列联表如图所示:
男生 12 4 16
女生 9 5 14
合计 21 9 30
零假设为: :对“数学建模”选修课的兴趣度与性别无关.
答案第8页,共2页根据 列联表数据计算可得: ,
根据小概率值 的独立性检验,没有充分证据推断 不成立,
因此认为 成立,即认为对“数学建模”选修课的兴趣度与性别无关. 7分
(2)由(1)可知对“数学建模”选修课的感兴趣的女生有9人,其中高三女生4人,
依题意可知 服从超几何分布,且 , , ;
的分布列为 , ;
即:
0 1 2 3
数学期望为 ,
(或 15分
17.(1)
(2) , 百万辆
【分析】(1)利用相关系数 公式即可求解;
(2)根据已知数据,利用公式先求出 ,进而求出 ,得到线性回归方程,再利用线性回
归方程进行预测即可.
【详解】(1)因为 ,
,
所以 ,
答案第9页,共2页
学科网(北京)股份有限公司,
所以 7分
(2)由题意得 ,
所以 ,
得 关于 的线性回归方程为 , 13分
所以可以预测2024年全球新能源汽车的销售量为 百万辆. 15分
18.(1)
(2)① ;②分布列见解析,
【分析】(1)根据题意可得旅游支出不低于 元的有 人,结合古典概型概率公式即
可求解;
(2)① 根据题意可得 , ,结合正态曲线的对称性即可求解;
②根据题意可得 所有可能取值为 ,结合二项分布求概率和均值即可求解.
【详解】(1)样本中总共 人,其中旅游支出不低于 元的有 人,
所以从中随机抽取两位市民的旅游支出数据,
两人旅游支出均不低于 元的概率为 ; 5分
(2)以下涉及旅游支出费用,则默认单位均为千元,
,
所以 , , 服从正态分布 ,
答案第10页,共2页,
,
估计襄阳市有 个市民每年旅游费用支出在 元以上;
②由①知, ,则 ,
的所有可能取值为 ,
, ,
, ;
所以随机变量 的分布列为:
均值为 . 17分
19.(1)分布列见解析,
(2)① ;②
【分析】(1)列出随机变量 的可能取值,并根据超几何分布计算每个可能取值的概率,
并计算分布列和数学期望;
(2)①根据第三次交流中甲被选择,第二次交流中甲未参与,计算概率即可;
②根据第 次被选择的概率,第 次未被选择的概率,得出数列递推公式
,再通过数列计算通项即可.
【详解】(1)由题随机变量 的所有可能取值为0,1,2,3,4.
答案第11页,共2页
学科网(北京)股份有限公司所以 的分布列为
0 1 2 3 4
所以随机变量 的数学期望 .8分
(2)①甲、乙两同学被同伴选择的概率均为 .
其他三名同学被选择的概率相等.
比赛由甲同学起稿建立模型,
第三次交流中甲被选择,
所以第二次交流中甲未参与.
设 “第三次交流中甲被选择”,
则 .
②第 次 交流中甲被选择,
则第 次交流中甲未被选择.
设第 次交流中甲被选择的概率为 .
答案第12页,共2页则 ,
所以 ,且 .
所以 ,
所以 . 17分
答案第13页,共2页
学科网(北京)股份有限公司