四川省成都市第七中学2024-2025学年高三下学期2月入学考试数学_2024-2025高三（6-6月题库）_2025年02月试卷_0216四川省成都市第七中学2024-2025学年高三下学期2月入学考试（全科）

成都七中高 2025 届高三下入学测试
一、单项选择题：本题共8 小题，每小题 5 分，共 40 分. 在每小题给出的四个选项中，只
有一项是符合题目要求的.
1．已知集合A  x∣y 3xx2  ,B  y∣y3x2  ．则AB（ ）
A．[0,3] B．(0,2] C．[2,3] D．(2,3]
2．若是第一象限角，则下列结论一定成立的是（ ）
 
A．sin 0 B．cos 0
2 2
  
C．tan 0 D．sin cos 0
2 2 2
       
3．设a,b为非零向量，则“ab”是“ ab  ab ”的（ ）
A．充分不必要条件 B．必要不充分条件
C．充分必要条件 D．既不充分也不必要条件
4．若复数z满足z2i2i，则在复平面内z对应的点位于（ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
y2
5．若双曲线x2  1的离心率是2，则实数k的值是（ ）
k
1 1
A．3 B． C．3 D．
3 3
6．某圆锥的侧面展开图是一个半径为2 6，圆心角为π的扇形，则该圆锥的内切球体积为
（ ）
8 2π 8 3π
A． B． C．4π D．6π
3 3
7．已知数列a 是各项为正数的等比数列，公比为q，在a,a 之间插入1个数，使这3个
n 1 2
数成等差数列，记公差为d ，在a ,a 之间插入2个数，使这4个数成等差数列，公差为d ,，
1 2 3 2
在a ,a 之间插入n个数，使这n2个数成等差数列，公差为d . 以下能使得数列d 单
n n1 n n
调递增的是（ ）
3
A.q 1 B.1 q  C.d d D.d d
1 2 2 3
2
8. 等腰三角形它的三个顶点都在曲线C:x2 m2y2 m2(m1)上，且该等腰三角形恰有
两个顶点在x轴或 y轴上.若满足以上条件的等腰三角形大于16 个，求m的范围（ ）
试卷第1页，共4页三、填空题：本题共3小题，每小题5分，共15分.
 
12. 经过点 1, 3 且与直线l:x 3y10垂直的直线方程为 .
 2n
13. 在 3 x  的二项式中，所有项的二项式系数之和为256，则常数项等于 ．
 x
14.
现有2n1个编号为1，2，，2n1  nN*，n2  的小球随机从中取出n个．记为取
出的n个球中最大的编号.对n2，E  _____ .
四、解答题：本题共5小题，共77分. 解答应写出文字说明、证明过程或演算步骤.
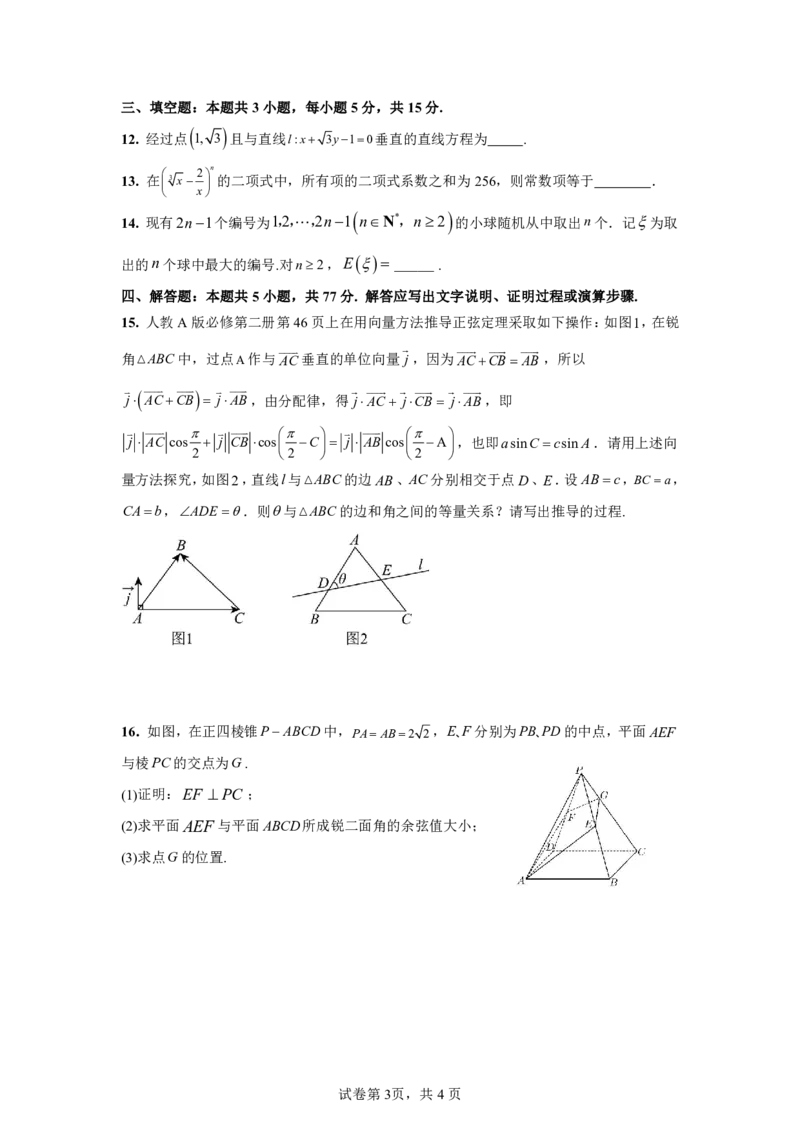
15. 人教A版必修第二册第46页上在用向量方法推导正弦定理采取如下操作：如图1，在锐
    
角VABC中，过点A作与AC垂直的单位向量 j，因为ACCBAB ，所以
            
j ACCB  jAB，由分配律，得 jAC jCB  jAB，即
          
j  AC cos  j CB cos C j  AB cos A，也即asinCcsinA．请用上述向
2  2   2 
量方法探究，如图2，直线l与VABC的边AB、AC分别相交于点D、E．设ABc，BCa，
CAb，ADE ．则与VABC的边和角之间的等量关系？请写出推导的过程.
16．如图，在正四棱锥PABCD中， PAAB2 2 ，E､F分别为PB､PD的中点，平面AEF
与棱PC的交点为G.
(1)证明：EF PC ；
(2)求平面AEF与平面ABCD所成锐二面角的余弦值大小；
(3)求点G的位置.
试卷第3页，共4页17. 已知定义在（0,）上的函数y f(x)的表达式为 f xsinxxcosx，其所有的零点按
从小到大的顺序组成数列x （n1,nN）.
n
 
(1)求函数y f x在 ,1处的切线方程；
 2 
(2)判断并证明函数y f x在区间 0,2025 上的零点个数；
(3)求证：x x .
n1 n
18. 如图，在一条无限长的轨道上，一个质点在随机外力的作用下，从位置0出发，每次只
能向左或者向右运动1个单位，且每次运动方向相互独立，质点向右运动的概率为
p(0 p1).设移动n次后质点位于位置 .
n
1
(1)当 p  时，求P  2  ；
4
2
1
(2)当 p  时，
3
①若n2025，求质点最有可能运动到的位置对应的数，并说明理由；
②求D
 
的值.
n
19.已知抛物线x2 2py(p 0)上有三点A,B,C .当 AB 10时，线段AB的中点M 的纵
19
坐标的最小值为 .
4
（1）求抛物线的方程；
（2）若以AC 为直径的圆过点B
①当B在坐标原点时，过B作AC的垂线，垂足为D，求D的轨迹方程；
3 3
②求证： AB  BC  .
2
试卷第4页，共4页