文档内容
华中师大一附中 2023-2024 学年度上学期高三期中检测
数学试题
命题人:余文抒 徐聪 王文莹 审题人:王文莹
试卷满分:150分 考试时间:120分钟
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有
一项是符合题目要求的.
1. 已知复数 满足 ,则 的模为( )
A. 1 B. 2 C. 5 D.
.
2 已知集合 ,则 ( )
A. B. C. D.
3. 在 中,“ ”是“ ”的( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
4. 已知函数 的图象的一部分如图1,则图2中的函数图像对应的函数是( )
A. B.
C. D.5. 在边长为2的正六边形 中, ( )
A. 6 B. -6 C. 3 D. -3
6. 在声学中,音量被定义为: ,其中 是音量(单位为dB), 是基准声压为
的
,P是实际声音压强.人耳能听到 最小音量称为听觉下限阈值.经过研究表明,人耳对于不同频
率的声音有不同的听觉下限阈值,如下图所示,其中240 对应的听觉下限阈值为20 ,1000 对应
的听觉下限阈值为0 ,则下列结论正确的是( )
A. 音量同为20 的声音,30~100 的低频比1000~10000 的高频更容易被人们听到.
B. 听觉下限阈值随声音频率的增大而减小.
C. 240 的听觉下限阈值的实际声压为0.002 .
D. 240 的听觉下限阈值的实际声压为1000 的听觉下限阈值实际声压的10倍.
7. 若实数 满足 ,则 的大小关系为( )
A. B.
C. D.
8. 已知函数 在区间 上恰有两个极值点,且 ,
则 的值可以是( )
A. 6 B. 7 C. 8 D. 9二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 已知函数 及其导函数 的部分图象如图所示,设函数 ,则 ( )
A. 在区间 上是减函数 B. 在区间 上是增函数
在
C. 时取极小值 D. 在 时取极小值
10. 已知 ,且 ,则( )
A. B.
C. D.
11. 若函数 在区间 有2024个零点,则整数 可以是( )
A. 2022 B. 2023 C. 2024 D. 2025
12. 已知定义在 上 的函数 图象上任意一点 均满足 ,且对任
意 ,都有 恒成立,则下列说法正确的是( )
A. B. 是奇函数
C. 是增函数 D.三、填空题:本题共4小题,每小题5分,满分20分
13. 若直线 与曲线 相切,则 __________.
14. 杭州第 届亚洲运动会,于 年 月 日至 月 日在中国浙江省杭州市举行,本届亚运会的会
徽名为“潮涌”,主体图形由扇面、钱塘江、钱江潮头、赛道、互联网符号及象征亚奥理事会的太阳图形
六个元素组成(如图),其中扇面造型突出反映了江南的人文意蕴.已知该扇面呈扇环的形状,内环和外环
均为圆周的一部分,若内环弧长是所在圆周长的 ,内环所在圆的半径为 ,径长(内环和外环所在圆的
半径之差)为 ,则该扇面的面积为__________.
15. 一只钟表的时针 与分针 长度分别为3和4,设0点为0时刻,则 的面积 关于时间 (单
位:时)的函数解析式为__________,一昼夜内(即 时), 取得最大值的次数为__________.
16. 如图,在四边形 中, ,则 面积的最大值
为__________.
四、解答题:本题共6小题,共70分,解答应写出必要的文字说明、证明过程或演算步骤.17. 已知
(1)求 的单调递增区间与对称中心;
(2)当 时, 的取值范围为 ,求实数 的取值范围.
18. 记 的内角 的对边分别为 ,已知 .
(1)求A的值;
(2)若 的平分线与 交于点 ,求 面积的最小值.
19. 已知函数 且 ,
(1)求函数 的单调区间;
(2)若函数 有最大值 ,求实数 的值.
的
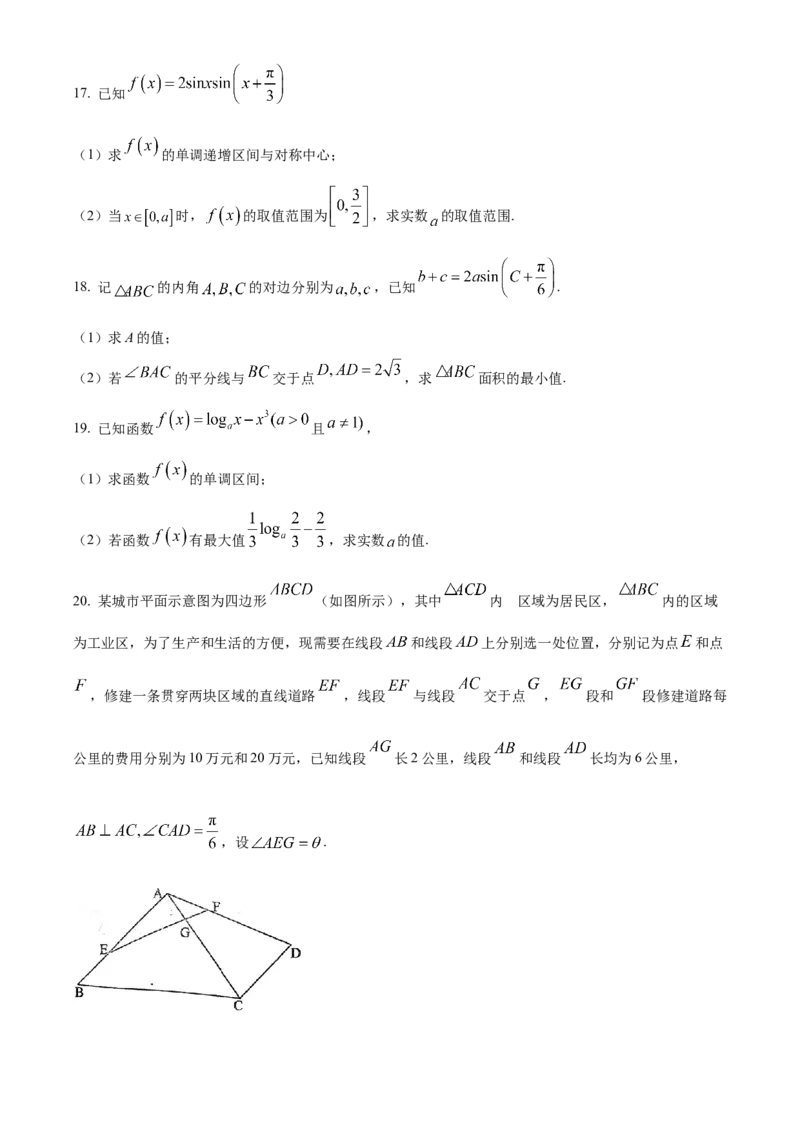
20. 某城市平面示意图为四边形 (如图所示),其中 内 区域为居民区, 内的区域
为工业区,为了生产和生活的方便,现需要在线段 和线段 上分别选一处位置,分别记为点 和点
,修建一条贯穿两块区域的直线道路 ,线段 与线段 交于点 , 段和 段修建道路每
公里的费用分别为10万元和20万元,已知线段 长2公里,线段 和线段 长均为6公里,
,设 .(1)求修建道路的总费用 (单位:万元)与 的关系式(不用求 的范围);
(2)求修建道路的总费用 的最小值.
21. 已知函数
(1)求 的零点个数;
(2)若 恒成立,求整数 的最大值.
22. 已知函数 有三个极值点 ,且 .
(1)求实数 的取值范围;
(2)若2是 的一个极大值点,证明: .