文档内容
四川省 2025 届新高三秋季入学摸底考试
数学试卷
试卷共 4页,19小题,满分 150分.考试用时 120分钟
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号等填写在答题卡指定位置上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上
无效. 3.考生必须保持答题卡的整洁.考试结束后,请将答题卡交回.
一、选择题:本题共 8小题,每小题 5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的
9−6i
+2i
1. i 的虚部为( )
A. −7 B. −6 C. −7i D. −6i
2. 已知等差数列 { a } 满足a =9,a =3,则a =( )
n 3 9 12
A. −2 B. 1 C. 0 D. −1
π
3. 3sin ( π−α)+sin +α =0,则tanα=( )
2
3 3 3 3
A. B. C. − D. −
2 3 2 3
x2 −4x,x≥0,
4. 函数 f
(
x
)=
的极值点个数为( )
−ex +1,x<0
A. 0 B. 1 C. 2 D. 3
( )
5. 已知某地区高考二检数学共有8000名考生参与,且二检的数学成绩X 近似服从正态分布N 95,σ2 ,
若成绩在80分以下的有1500人,则可以估计P ( 95≤ X ≤110 )=( )
5 5 11 3
A. B. C. D.
32 16 32 16
6. 定义:如果集合U 存在一组两两不交(两个集合的交集为空集时,称为不交)的非空真子集
A,A,,A ( k∈N* ),且A A A =U ,那么称子集族 { A,A,,A } 构成集合U 的 一个
1 2 k 1 2 k 1 2 k
第1页/共4页
学科网(北京)股份有限公司k划分.已知集合I ={x∈N| x2 −6x+5<0},则集合I 的所有划分的个数为( )
A. 3 B. 4 C. 14 D. 16
7. 已知圆台的上、下底面的面积分别为4π,25π,侧面积为35π,则该圆台外接球的球心到上底面的距离
为( )
27 27 37 37
A. B. C. D.
8 4 8 4
8. 已知O为坐标原点,抛物线C:x2 =2py(p>0)的焦点F 到准线l的距离为1,过点F 的直线l 与C
1
交于M,N 两点,过点M 作C的切线l 与x,y轴分别交于P,Q两点,则PQ⋅ON =( )
2
1 1 1 1
A. B. − C. D. −
2 2 4 4
二、选择题:本题共 3小题,每小题 6分,共18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得 6分,部分选对的得部分分,有选错的得 0分
x π x
9. 已知函数 f ( x )=3sin + ,g ( x )=3cos ,则( )
2 3 2
( )
A. f x 的最小正周期为4π
( ) ( )
B. f x 与g x 有相同的最小值
C. 直线x = π为 f ( x ) 图象的一条对称轴
π
( ) ( )
D. 将 f x 的图象向左平移 个单位长度后得到g x 的图像
3
1
10. 已知函数 f ( x )= x3 −x,f′( x )为 f ( x ) 的导函数,则( )
3
A.
f′(
0
)=0
B. f
(
x
)
在
( 1,+∞)
上单调递增
2
( )
C. f x 的极小值为
3
1
D. 方程 f ( x )= 有3个不等的实根
2
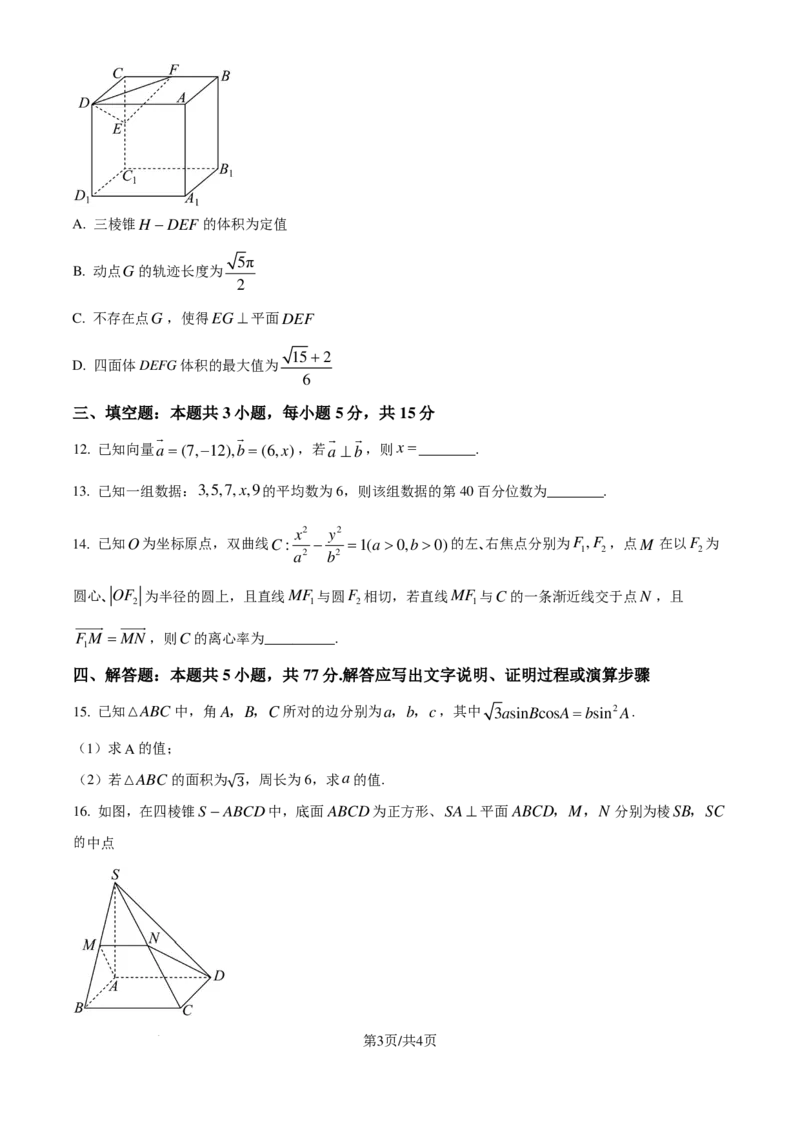
11. 已知正方体ABCD− ABC D 的体积为8,线段CC ,BC的中点分别为E,F,动点G在下底面
1 1 1 1 1
ABC D 内(含边界),动点H 在直线AD 上,且GE = AA ,则( )
1 1 1 1 1 1
第2页/共4页
学科网(北京)股份有限公司A. 三棱锥H −DEF 的体积为定值
5π
B. 动点G的轨迹长度为
2
C. 不存在点G,使得EG ⊥平面DEF
15+2
D. 四面体DEFG体积的最大值为
6
三、填空题:本题共 3小题,每小题 5分,共 15分
12. 已知向量a =(7,−12),b=(6,x),若a ⊥b,则x=________.
13. 已知一组数据:3,5,7,x,9的平均数为6,则该组数据的第40百分位数为________.
x2 y2
14. 已知O为坐标原点,双曲线C: − =1(a >0,b>0)的左、右焦点分别为F,F ,点M 在以F 为
a2 b2 1 2 2
圆心、 OF 为半径的圆上,且直线MF 与圆F 相切,若直线MF 与C的一条渐近线交于点N ,且
2 1 2 1
FM =MN ,则C的离心率为__________.
1
四、解答题:本题共 5小题,共 77分.解答应写出文字说明、证明过程或演算步骤
15. 已知ABC中,角A,B,C所对的边分别为a,b,c,其中 3asinBcosA=bsin2A.
(1)求A的值;
(2)若ABC的面积为 ,周长为6,求a的值.
16. 如图,在四棱锥S −A√B3CD中,底面ABCD为正方形、SA⊥平面ABCD,M,N 分别为棱SB,SC
的中点
第3页/共4页
学科网(北京)股份有限公司(1)证明:MN //平面SAD;
(2)若SA= AD,求直线SD与平面ADNM 所成角的正弦值
x2 y2 2 2 3
17. 已知椭圆C: + =1(a >b>0)的离心率为 ,右焦点为F ,点(− , )在C上.
a2 b2 2 2 2
(1)求C的方程;
(2)已知O为坐标原点,点A在直线l: y =kx+m ( k ≠0 ) 上,若直线l与C相切,且FA⊥l ,求 OA
的值.
18. 已知函数 f
(
x
)=lnx−x+a.
(1)若a =0,求曲线 在 处的切线方程;
(2)若 时 f ( x )<𝑦𝑦0=,𝑓𝑓求 (𝑥𝑥a) 的𝑥𝑥取=值1范围;
𝑥𝑥 >0
(3)若00,在所有 { a }( 1≤n≤4 ) 中随机抽取2个数列,记满足a <0的数列 { a } 的个数为X ,求
2 n 4 n
X 的分布列及数学期望EX ;
(2)若数列 { a } 满足:若存在a ≤−5,则存在k∈{ 1,2,,m−1 }( m≥2且m∈N* ) ,使得
n m
a −a =4.
k m
(i)若a >0,证明:数列 { a } 是等差数列,并求数列 { a } 的前n项和S ;
2 n n n
(ii)在所有满足条件的数列 { a } 中,求使得a +2025=0成立的s的最小值.
n s
第4页/共4页
学科网(北京)股份有限公司