巴蜀中学高二10月月考数学答案_2024-2025高二（7-7月题库）_2024年11月试卷_11062024-2025学年重庆市巴蜀中学高二10月月考

高 2026 届高二上月考数学参考答案
一、单选题
题号 1 2 3 4 5 6 7 8
答案 C B D B C D A D
1【详解】设直线的 x  y  3  0 的倾斜角为，且  0 , π    ，直线 x  y  3  0 的斜率
k t a n 1    ，所以
π
4
  ，故选：C
2【详解】点 到两个定点 ， 的距离之和等于常数 ，由椭圆的定
义可知：此点的轨迹为焦点在 轴上的椭圆，且 ，故 ，故椭圆的标准
x2 y2
方程为  1.故选：B
6 3
3【详解】解：由题意，圆心坐标为点C1,5，半径为 1 2  5 2  2 6 ，
则圆的方程为 ( x  1 ) 2  ( y  5 ) 2  2 6 ．故选：D．
4【详解】两圆方程相减得公共弦方程为 x  y  2  0 .
5【详解】由题设，圆 C 的圆心为 ( 2 , 4 ) ，且半径 r  1 0 ，
而122 242 510，即点  1 , 2  在圆内，且圆心到该点的距离d  5 ，
当直线 l 与
1,2
、 ( 2 , 4 ) 的连线垂直时，弦长最短为 2 r 2 d 2 2 5 ，
故长度为 2 5 的弦的条数为1条. 故选：C
6【详解】直线 A A ' 的斜率为 
1
3
，直线l为线段AA'的中垂线，从而 k 3，
又线段 A A ' 的中点 (  1 , 2 ) 在 l 上，故23b，解得 b  5 ，故选：D.
7【详解】依题意 F （2 2 , 0 ） ，直线 P Q 的方程为 y  （3 x  2 ） 即 y  3 x  6
 9
x2 y2 y 
  1   1 4
联立10 6 解得8y2 6y270  从而
3
 
y 3x6 y 
 2 2
y
1
 y
2

1 5
4
PQF 的周长为
1
4 a  4 1 0
Px,y
1 15 15
，面积为S  FF y  y 2 
2 1 2 1 2 4 2
1 15 3 10
又S  4ar 2 10r  所以 r  故选：A
2 内 内 2 内 8
 3 , 0    3 , 0  2 6
x a  6 , c  3 b  3
{#{QQABTQAEggAAQBJAAQgCQQ0gCAGQkhECAagOxBAIoAAASQFABAA=}#}8【详解】 圆 M 与x轴相切于焦点 F ，MF x轴，可设 M  c , y  ，
M 在椭圆上， 
c
a
2
2

y
b
2
2
 1 ，解得： y  
b
a
2
，  圆 M 的半径为
b
a
2
；
作 M N  y 轴，垂足为 N ，
M P  M Q ，   P M N   N M Q ，
P M Q 为直角三角形，   N M Q 
π
4
，  c 
2
2

b
a
2
，
 2 a c  a 2  c 2 ，即 2 e  1  e 2 ，解得： e 
6 
2
2
，
故选：D.
二、多选题
题号 9 10 11
答案 BD BCD ACD
9【详解】A选项：当直线过原点时，方程为 y   x ，
当直线不过原点时，设方程为
2
x
b

y
b
 1 ，则

2
1
b
0

1 0
b
 1 ，解得 b   4 ，
所以直线方程为 x  2 y  1 0  0 ，综上，所求直线方程为 x  y  0 或x2y80，故
A错误；
B选项：由方向向量的定义知正确；
C选项：直线xy10，即为 2 x  2 y  2  0 ，
故直线 x  y  1  0
21 3 2
与直线2x2y10之间的距离为  ，故C错误；
44 4
D选项：直线xcos 3y20R的斜率 k
3
3
c o s
3
3
,
3
3
   



，
 π 5π 
所以倾斜角的范围是

0,



,π，故D正确；
 6  6 
故选：BD.
{#{QQABTQAEggAAQBJAAQgCQQ0gCAGQkhECAagOxBAIoAAASQFABAA=}#}10【详解】解：A选项：由椭圆方程
x
8
2

y
4
2
 1 ，所以 a 2  8 ，b2 4，所以
FPF
c2 a2 b2 4，所以FPF 的面积为S b2tan 1 2 4，故A错误；
1 2 2
B选项：当 P F
1
 F
1
F
2
或 P F
2
 F
1
F
2
时  F
1
P F
2
为直角三角形，这样的点 P 有4个，设椭
圆的上下顶点分别为 S , T ,计算知FSF FTF 90,所以当P位于椭圆的上、下顶
1 2 1 2
点时  F
1
P F
2
也为直角三角形，其他位置不满足，满足条件的点 P 有6个，故B正确；
C选项：由于 PF 2 PF 4 23PF ，所以当
1 2 2
P F
2
最小即 PF ac2 22时
2
PF 2 PF 取得最大值
1 2
6  2 2 ；故C正确；
D选项：因为 P F
1
 P M  2 a  P F
2
 P M  4 2  P M  P F
2
，又
P M  P F
2
 M F
2

2
5
，当点 P 位于直线MF 与椭圆的交点时取等号，故D正确．
2
故选：BCD
11【详解】A选项：设 M ( x , y ) 则：由
M
M
D
E
 2
x2 (y2)2
得 2，化简得：
x2 (y1)2
x 2   y  2  2  4 ，故曲线C的方程为 x 2   y  2  2  4 ，A选项正确；
B 选项： C:x2 y22 4的圆心 C ( 0 ,  2 ) 到直线l的距离为
1 2
5
 2 ，所以直线 l 与
C 相离，从而圆上动点 M 到直线 l
12 2
距离的最小值为 r  ，从而B选项错误；
5 5
C选项： R T P A C
2
12 2 11
中， PA  PC2 CA2  d2 r2  22  ，故C  
 5  5
正确；
MD
3
D选项：N( ,0)，因为 2所以
2 ME
M D  2 M E
所以 M D  2 M N  2

M E  M N

2
 3
2 EN 2  12  13，
 
 2
当且仅当M 在线段EN 与圆C的交点时取得最小值，故D正确.
故选：ACD
三、填空题
{#{QQABTQAEggAAQBJAAQgCQQ0gCAGQkhECAagOxBAIoAAASQFABAA=}#}题号 12 13 14
答案
x  y  4  0 m 
1
1
3
或
1
5
9  2 1 0
12【详解】 k
C A
  1  k
切
 1 ，又过点 （A 2 ,  2 ） ，所以切线方程为 x  y  4  0
13【详解】将 ( 0 , 3 ) 代入椭圆方程 C : m x 2  n y 2  1 ，解得 n 
1
9
；故椭圆方程为
m x 2 
y
9
2
 1 .由焦距为4，得c2，c2 4.
由题意知 m  0 ，且m 
1
9
x2 y2
 1
，方程可化为 1 9 ，
m
若椭圆焦点在 x
1
轴上，故a2  ,b2 9，则有
m
c 2 
1
m
 9  4 ，解得 m 
1
1
3
；
若椭圆焦点在 y
1
轴上，a2 9,b2  ，则有
m
c 2  9 
1
m
 4 ，解得 m 
1
5
；
综上所述， m 
1
1
3
或
1
5
.
14【详解】曲线 y  1  4  x 2 即 x 2  ( y  1 ) 2  4 ( y  1 ) ，由于P(a,b)在曲线上，令
a
b
2
1
c o
2
s
s i n
( 0 )

 

 
 
  则
a b 3 a 2 b 2 2
2
4
9
c
c
o
o
2
6
s
s
s
s
i n
i n
1
2 s
2
i n
2
2
s
c
c
i
o
o
n
s
s
4
3
5
5
9
 2
4
4 s
2
c o
s i n
i n
1 0
s
s i

n
2
(
 1
)
2 s i n  2    
  
  
   
    






















1 3
（其中sin ,cos ，不妨设
10 10
0 ,
2

 
 
）
 0 ,   ,              又
2
, 0 ,
2
,
 
     



 
 
2

   当   时 a  b  3  a 2  b 2 取得最大值92 10.
四、解答题
15【答案】(1) m0或2， (2) x2y10．
【详解】（1） l //l m12 1 解得m0或2
1 2
{#{QQABTQAEggAAQBJAAQgCQQ0gCAGQkhECAagOxBAIoAAASQFABAA=}#}当 m  0 时， l1 ：x y10， l2 ： x  y  4  0 满足 l1 / / l
2
；
当 m   2 时， l1 ： x  y  1  0 ， l2 ：  x  y  4  0 即 x  y  4  0 满足 l1 / / l
2
；
故 m  0 或  2
（2） （A  1 , 0 ） ， （B 0 , 4 ）
当m1时联立l与l 的方程：
1 2
 x
2

x
2

y
y


1
4


0
0
解得C(3,2) k 2 ，从而
BC
k
l

1
2
又 直线 l 过点A（1,0） 故直线 l 的方程为 y 
1
2
( x  1 ) 即 x  2 y  1  0
16【答案】(1)
x
4
2

y
3
2
 1 ， (2)
3
4
3
．
b 3
a2

 c 1 
【详解】（1）由题e  b 3
a 2  
c1
a2 b2 c2 

 C :
x
4
2

y
3
2
 1
（2）设 M ( x
1
, y
1
) , N ( x
2
, y
2
) ，线段 M N 中点 Q ( x
0
, y
0
) 则
F
2
为 B M N 的重心 
 x
y
1
1

3

x
y
2
23


1
3
 0
从而
 x
y
1
1


x
y
2
2


3
 3
所以

x
y
0
0


3
2

2
3
即 Q (
3
2
, 
2
3
)
M , N
x2 y2
1  1 1

 4 3 y 3
均在椭圆C上  作差可得 k  0  带入Q点坐标得
x
2
2

y
2
2
1
MN x
0
4
 4 3
3 3
k 
MN 4
{#{QQABTQAEggAAQBJAAQgCQQ0gCAGQkhECAagOxBAIoAAASQFABAA=}#} 3
2
4
 2



2
3
3 
2

1
1
3
6
 1
 Q 在椭圆内部，所求直线 M N 存在
故 直线 M N
3 3
的斜率为
4
17【答案】(1)证明见解析 (2)
7
1 8
6
．
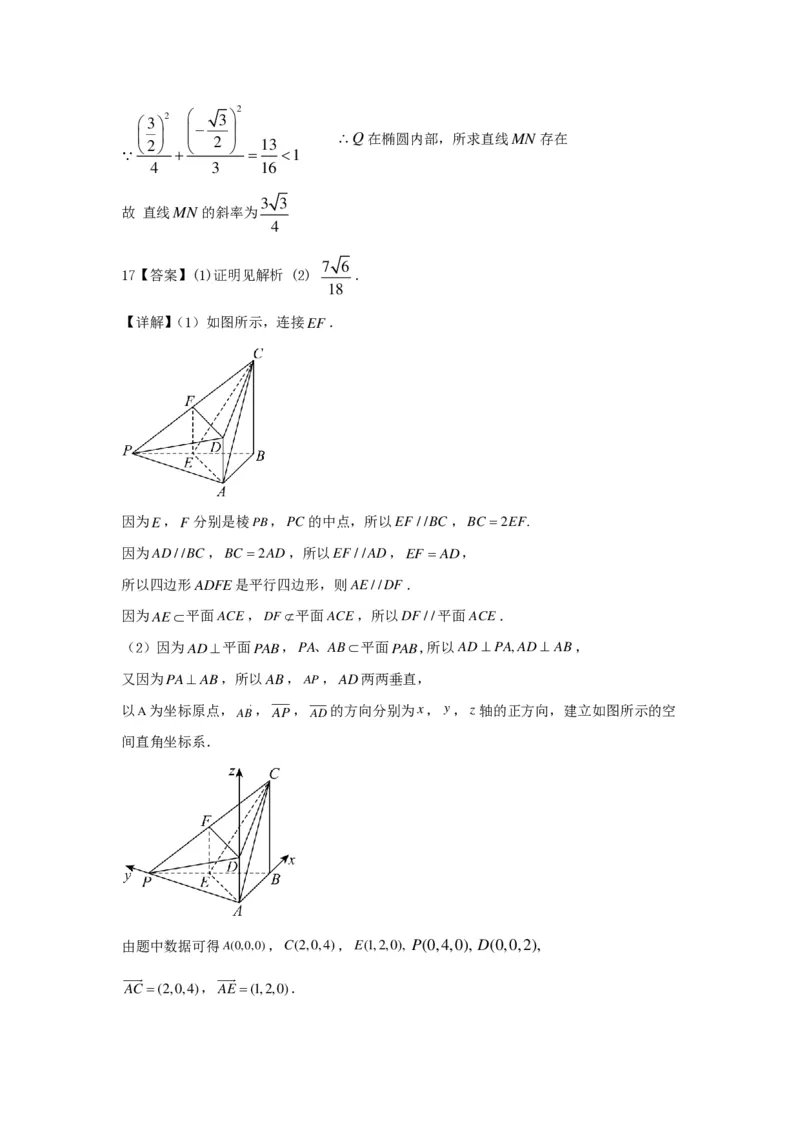
【详解】（1）如图所示，连接 E F ．
因为 E ， F 分别是棱PB， P C 的中点，所以EF //BC， B C  2 E F .
因为 A D / / B C ， B C  2 A D ，所以 E F / / A D ， E F  A D ，
所以四边形 A D F E 是平行四边形，则AE//DF．
因为 A E  平面 A C E ， D F  平面 A C E ，所以 D F / / 平面 A C E ．
（2）因为 A D  平面 P A B ， P A 、 A B  平面 P A B ,所以 A D  P A , A D  A B ，
又因为 P A  A B ，所以AB， A P ，AD两两垂直，
以 A 为坐标原点， A B ，AP， A D 的方向分别为x，y， z 轴的正方向，建立如图所示的空
间直角坐标系．
由题中数据可得 A ( 0 , 0 , 0 ) ，C(2,0,4)，E(1,2,0), P ( 0 , 4 , 0 ) , D(0,0,2),
AC(2,0,4)，AE(1,2,0)．
{#{QQABTQAEggAAQBJAAQgCQQ0gCAGQkhECAagOxBAIoAAASQFABAA=}#}设平面 A C E 的法向量为 n  ( x , y , z ) ，则
 n
n
 A
 A
C
E


2
x
x


2
4
y
z 

0 ,
0 ,
令x2，得n(2,1,1)．
同理可求得平面 P C D 的一个法向量为 m  ( 2 ,  1 ,  2 ) ．
设平面ACE与平面 P C D 的夹角为，
|nm| 7 6
则cos|cosn,m|  ．
|n||m| 18
即平面 A C E 与平面 P A D
7 6
的夹角的余弦值为 ．
18
18【答案】(1)  x  2  2  y 2  4
2 5 2 5
(2)（Ⅰ）k( ,0)(0, )；（Ⅱ）k k 5
1 2
5 5
（定值）
【详解】（1）设Ax,y， M  x
0
, y
0
 ，由中点坐标公式得

x
y
0
0


x
y

2
2
6
4
,
．
因为点 M 的轨迹方程是 ( x  4 ) 2  ( y  2 ) 2  1
x6  2  y4  2
，所以  4  2 1，
 2   2 
整理得曲线 C 的方程为 ( x  2 ) 2  y 2  4 ．
（2）设直线 l 的方程为 y  （k x  1 ） ， E ( x
1
, y
1
) , F ( x
2
, y
2
) ，联立直线 l 和曲线C的方
程：
 y
( x


k
2
x
)

2
k
 y 2  4
消去 y 得： （ 1  k 2 ) x 2  ( 2 k 2  4 ) x  k 2  0
（Ⅰ）因为直线l与曲线 C 交于异于坐标原点的两点E,F，所以

  2k2 4 2 4k2(1k2)4(45k2)0

 42k2
x x  解得
1 2 1k2

 k2
x x  0
 1 2 1k2
{#{QQABTQAEggAAQBJAAQgCQQ0gCAGQkhECAagOxBAIoAAASQFABAA=}#}k  ( 
2
5
5
, 0 )  ( 0 ,
2
5
5
)
(Ⅱ) k
1
k
2

y
x
1
1
y
x
2
2

k 2 ( x
1

x
1
1
)
x
(
2
x
2
 1 )
 k 2
x
1
x
2
 x
1
x x
1

2
x
2
 1
带入韦达得：
k
1
k
2
 k 2
1
k

2
k 2

1
4
1
k



2
k 2
2
k
k
2
2
 1
 k 2 
5
k 2
 5 （定值）
19【答案】(1) x 2  y 2  4 (2)见详解；（3） S  [
4
3
6
, 6 ]
【详解】（1）椭圆C：
x
3
2
 y 2  1 中 a 2  3 , b 2  1 ，所以所求圆E的方程为
x 2  y 2  4 ；
x 2
（2）设A（x ,y），则 0  y 2 1
0 0 3 0
 y
0
2  1 
x
0
3
2
又 （F
1
- 2 , 0 ） 、 F （2 2 , 0 ）
 A F
1
 （ x
0
 2 ） 2  y
0
2  （ x
0
 2 ） 2  1 
x
0
3
2

2
3
x
0
2  2 2 x
0
 3  3 
3
6
x
0
6
同理 AF  3 x
2 3 0
 A F
1
 A F
1
 3 
2
3
x
0
2
A S  A T （ 2  O A ） （ 2 - O A ） = 4  O A 2  4  x
0
2  y
0
2  4  x
0
2 

1 
1
3
x
0
2

 3 
2
3
x
0
2
 A S  A T  A F
1
 A F
2
（3）①当l 斜率不存在，
1
l
2
斜率为0时，l 方程为
1
x  1 ，原点到l 的距离为
1
d
1
 1 所以
P Q  2 4  d
1
2  2 3 ， MN 2 3，所以四边形 P M Q N
1
面积S  PQ  MN 6;
2
②当 l1 斜率存在， l
2
斜率不为 0 时，设 l
2
的方程为xmy1，则 l1 的方程为
y m(x1)即 m x  y  m  0
m
则 原点到l 的距离为 d 
1 1
m2 1
{#{QQABTQAEggAAQBJAAQgCQQ0gCAGQkhECAagOxBAIoAAASQFABAA=}#}所以 P Q  2 4  d
1
2  2 4 
m
m
2
2
 1
 2
3 m
m
2
2


4
1
设 M （ x
1
, y ）1 、 （N x
2
, y ）2 ，联立 l
2
与 C 的方程，即
 x
x
3

2

m y
y 2


1
1
消去 x 得 （ m 2  3 ) y 2  2 m y  2  0
由于A(1,0)在椭圆C内部，所以直线 l
2
与C必相交且

y
y
1
1

y
2
y

2

m


2
2

m
2
2
3
m
 3
所以
M N 

1
1


m
m
2
2
y
(
1


m
y
2
2
2
m


3
) 2
1


4
m
m
2

2
2

( y
3
1


y
2
2
2 )
（3

1
4

m
y
m
1
2
y
2

2
) (
3
m 2  2 )
因为 l1  l
2
所以四边形PMQN面积
1 3m2 4 2 3(m2 1)(m2 2) 2 3(3m2 4)(m2 2)
S  PQ  MN   
2 m2 1 m2 3 m2 3
3(3m2 4)(m2 2)
2
 m2 3 2
令 t  m 2  3 ( t  3 ) 则m2 t3 故
S 

1
2
2
P
3
Q 
5 (
M
1
t
N

4
5

) 2
2

1
5
3 ( 3 t  5
t
)
2
( t  1 )
 2 3
3 t 2 
t
8
2
t  5
 2 3
5
2 t

8
t
 3
1 1 1 1
t 3  (0, ] 令u  ,则u(0, ]则
t 3 t 3
4 1 1
S 2 3 5(u )2  在u(0, ]单调递减
5 5 3
{#{QQABTQAEggAAQBJAAQgCQQ0gCAGQkhECAagOxBAIoAAASQFABAA=}#}1 4 6
当u  时 S  ； 当
3 min 3
u  0 时， S  6 所以 S  [
4
3
6
, 6 )
4 6
综上： S [ ,6]
3
{#{QQABTQAEggAAQBJAAQgCQQ0gCAGQkhECAagOxBAIoAAASQFABAA=}#}