四川省宜宾市2025届高三第一次诊断性考试数学_2024-2025高三（6-6月题库）_2024年11月试卷_1124四川省宜宾市2025届高三第一次诊断性考试（全科）

宜宾市普通高中 2022 级第一次诊断性测试 数 学 （考试时间：120分钟；全卷满分：150分） 注意事项： 1．答卷前，考生务必将自己的考号、姓名、座位号填写在答题卡上。 2．回答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。如 需改动，用橡皮擦擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上。写 在本试卷上无效。 3．考试结束后，将本试卷和答题卡一并交回。 一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只 有一项是符合题目要求的。 1．如图，在复平面内，网格中每个正方形的边长都为1，点A，B对 应的复数分别为z ，z ，则 z z  1 2 1 2 A. 13 B. 10 C. 3 D. 5 2．下列函数中，既是奇函数，又在(0，)上为增函数的是 A． f(x)ex ex B． f(x)ex ex C． f(x) x3 D． f(x) xln x 3π cos 3．若(π， )，tan ，则sin 2 sin1 3 2 1 1 A． B． C. D． 2 2 2 3 4．已知随机变量B(n，p)，若E()2，D()1，则P(2) 1 1 3 1 A． B． C． D． 8 4 8 2 5．已知向量a，b满足 a 1， ab 2，且(ba)b，则 b  A．1 B． 2 C． 3 D．2 6．从标有数字1，2，3，4，5，6的六张卡片中无放回随机抽取两张，则抽到的两张卡片数字 之积是3的倍数的概率为 3 1 3 2 A． B． C． D． 10 3 5 3 5 3log 2 7．已知a ， b 3 ，c 3 ，则 3 2 A．abc B．acb C．bca D．cba 一诊测试 数学 第 1 页 共 4 页2 8．a 是函数 f(x)axcosxsinx1在x(0，π)上有零点的 π A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中，有多项 符合题目要求。全部选对的得6分，部分选对的得部分分，有选错的得0分。 9．某社会机构统计了某市四所大学2024年的毕业生人数及自主创业人数如下表： A大学 B大学 C大学 D大学 毕业生人数x（千人） 3 4 5 m 自主创业人数 y （千人） 0.1 0.2 0.4 0.5 根据表中数据得到自主创业人数y关于毕业生人数x的经验回归方程为yˆ 0.14x0.33，则 A． y 与x正相关 B．m6 C．当x3时，残差为0.01 D．样本的相关系数r为负数 10．设函数 f(x)2x3 3x2 1，则 π A．x0是 f(x)的极大值点 B． f(sinx)在(0， )单增 2 3 C． f(x) f(1x)1 D． f(x ) f(x) 2 11．已知函数 f(x)及其导函数 f(x)的定义域均为R，记g(x) f(x)．若 f(12x)与g(2x)均 为偶函数，则 2024 A． f(0)0 B．g(2)g(2) C． f(0) f(2) D．g(k)0 k1 三、填空题：本题共3小题，每小题5分，共15分。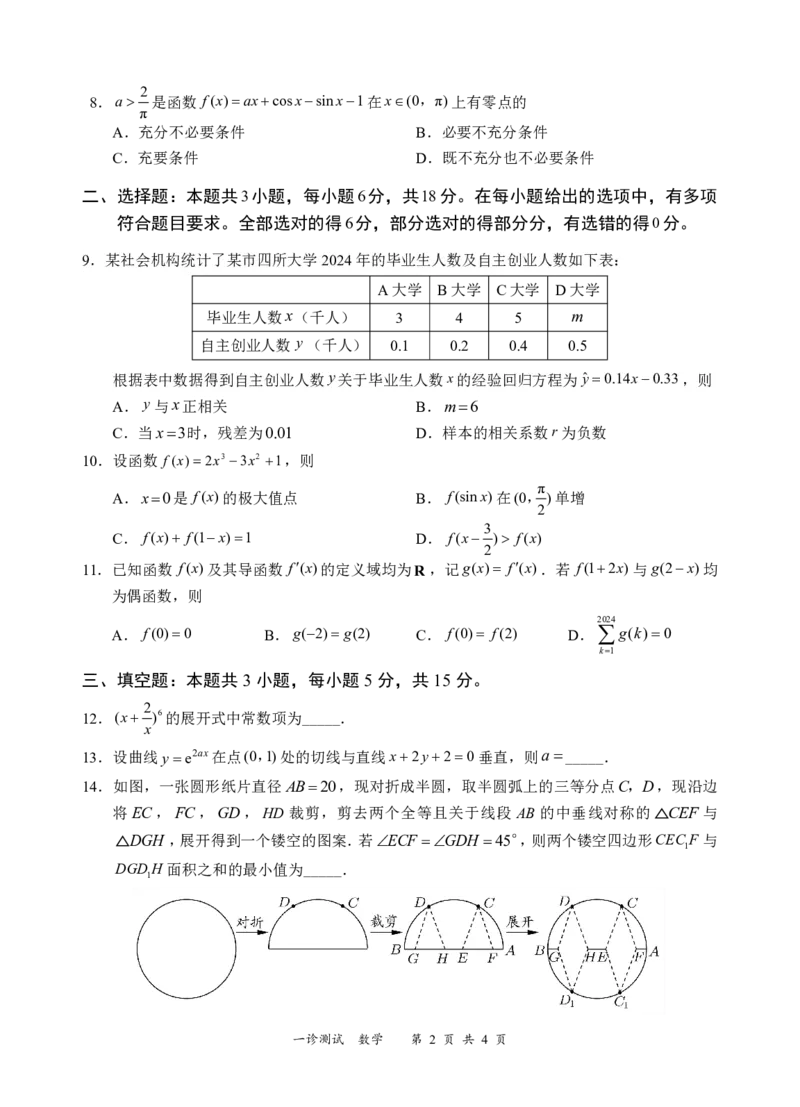 2 12．(x )6的展开式中常数项为_____． x 13．设曲线ye2ax在点(0，1)处的切线与直线x2y20垂直，则a_____． 14．如图，一张圆形纸片直径AB20，现对折成半圆，取半圆弧上的三等分点C，D，现沿边 将EC，FC，GD，HD 裁剪，剪去两个全等且关于线段 AB 的中垂线对称的△CEF 与 △DGH ，展开得到一个镂空的图案．若ECF GDH 45°，则两个镂空四边形CEC F与 1 DGDH 面积之和的最小值为_____． 1 一诊测试 数学 第 2 页 共 4 页四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。 15．（13分） 如图，正四棱柱ABCDA B C D 中，M 为DD 的中点，AB 1，AA 2． 1 1 1 1 1 1 （1）求证：平面B MC 平面AMC； 1 （2）求平面MAC与平面BAC的夹角的余弦值． 1 16．（15分） 3 现有甲、乙两个靶，某射手向甲靶射击两次，每次命中的概率为 ，每命中一次得1分，没 4 1 有命中得0分；向乙靶射击一次，命中的概率为 ，命中得2分，没有命中得0分．假设该射手 4 完成以上三次射击，且每次射击的结果相互独立． （1）求该射手恰好命中一次的概率； （2）求该射手的总得分X 的分布列及数学期望E(X)． 17．（15分） 已知函数 f(x)2 3sinxcosx2sin2x1，在锐角△ABC中，内角A，B，C的对边分别为 a，b，c ，且 f(A)1． （1）求A； （2）若b1，求4a22c的取值范围． 一诊测试 数学 第 3 页 共 4 页18．（17分） x2 y2 5 已知O为坐标原点，双曲线C：  1(a0，b0)的离心率为 5，且过点P（ ，1）． a2 b2 2 （1）求C的标准方程； （2）过C的右焦点F 的直线l 与双曲线C的左、右两支分别交于A，B两点，点Q是线段AB 1    的中点，过点F 且与l 垂直的直线l 交直线OQ于点M ，点N满足MN MAMB． 1 2 ①证明：点M 在一条定直线上； ②求四边形MANB面积的最小值． 19．（17分） 已知函数u(x)2lnxa(x2 1)，v(x)2x2lnx． （1）当a1时，判断u(x)的单调性； （2）若函数 f(x)u(x)v(x)恰有两个极值点． ①求实数a的取值范围； ②证明： f(x)的所有零点之和大于3． 一诊测试 数学 第 4 页 共 4 页