文档内容
汕头市潮阳实验学校 学年度第⼀学期第⼆次⽉考考试
2025~2026
⾼⼆数学试卷
⼀、单选题:本题共8⼩题,每⼩题5分,共40分.
1. 已知集合 ,则 ( )
A [2,4] B. C. D.
2. 已知复数 满⾜ ,则复数 在复平⾯内对应的点位于( )
A. 第⼀象限 B. 第⼆象限 C. 第三象限 D. 第四象限
3. 已知向量 , ,且 ,则 的值为( )
A. B.2 C. D.8
4. 已知等差数列 的公差为1, ,则 ( )
A. B. C. D.
5. 若 ,则( )
A. B. C. D.
6. 已知 ,则 ( )
A. B. C. D.
7. 已知过球⾯上 三点的截⾯和球⼼的距离等于球半径的⼀半,且 ,则球⾯积是
A. B. C. D.
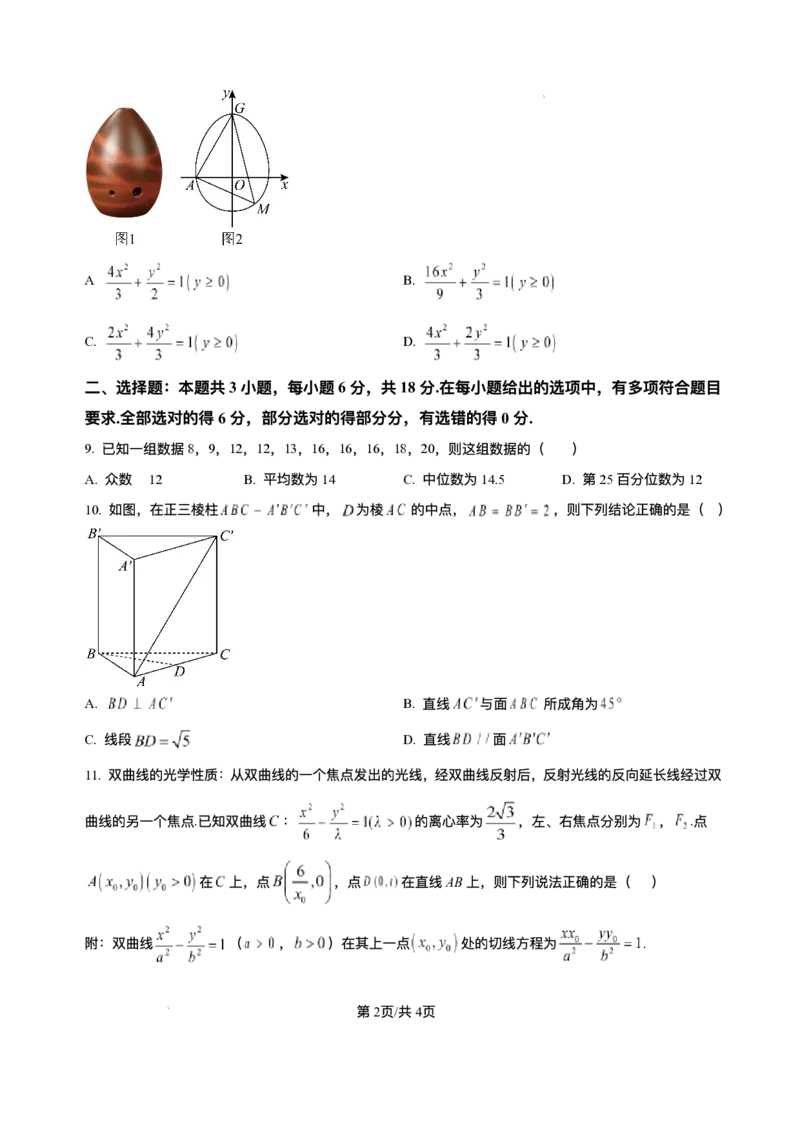
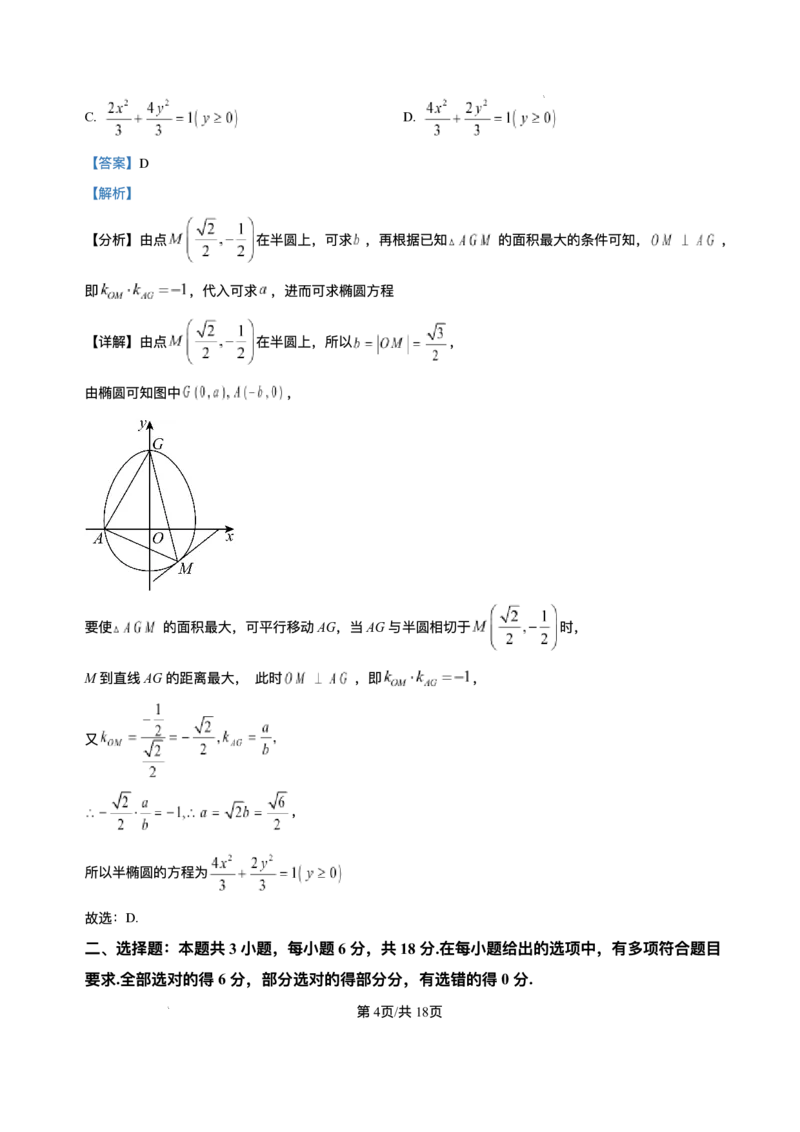
8. 吹奏乐器“埙”(如图1)在古代通常是⽤陶⼟烧制的,⼀种“埙”的外轮廓的上部是半椭圆,下部是半圆,
已知半椭圆 ( 且为常数)和半圆 组成的曲线C如图2所
示,曲线C交x轴的负半轴于点A,交y轴的正半轴于点G,点M是半圆上任意⼀点,当点M的坐标为
时, 的⾯积最⼤,则半椭圆的⽅程是( )
第1⻚/共4⻚
学科⽹(北京)股份有限公司A B.
C. D.
⼆、选择题:本题共3⼩题,每⼩题6分,共18分.在每⼩题给出的选项中,有多项符合题⽬
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 已知⼀组数据8,9,12,12,13,16,16,16,18,20,则这组数据的( )
A. 众数 12 B. 平均数为14 C. 中位数为14.5 D. 第25百分位数为12
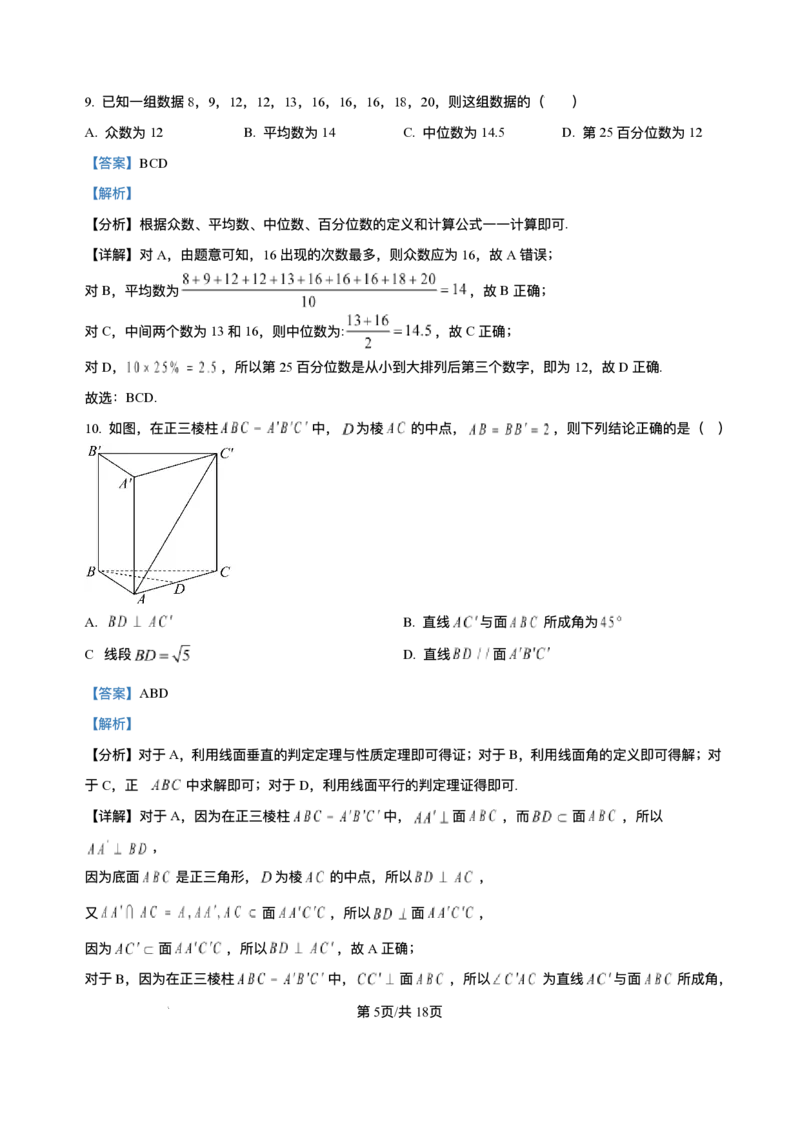
10. 如图,在正三棱柱 中, 为棱 的中点, ,则下列结论正确的是( )
A. B. 直线 与⾯ 所成⻆为
C. 线段 D. 直线 ⾯
11. 双曲线的光学性质:从双曲线的⼀个焦点发出的光线,经双曲线反射后,反射光线的反向延⻓线经过双
曲线的另⼀个焦点.已知双曲线 : 的离⼼率为 ,左、右焦点分别为 , .点
在 上,点 ,点 在直线AB上,则下列说法正确的是( )
附:双曲线 ( , )在其上⼀点 处的切线⽅程为 .
第2⻚/共4⻚
学科⽹(北京)股份有限公司A.
B.
C. 作 于点 ,则 ( 为坐标原点)
D. 若 延⻓线交 于点 ,则 的内⼼在定直线上
三、填空题:本题共3⼩题,每⼩题5分,共15分.
12. 已知抛物线 的准线 与双曲线 相切,则双曲线 的离⼼率 ________.
13. 已知圆⼼为 ,直线 与圆 相切于点 ,则圆 的半径⻓为_____.
14. 在斜 中, 为锐⻆,且满⾜ ,则 的最⼩值为
______.
四、解答题:本题共5⼩题,共77分.解答应写出⽂字说明、证明过程或演算步骤.
15. 袋⼦中有5个⼤⼩质地完全相同的球,其中2个红球,3个⻩球.
(1)若这5个球分别标有数字 , , , , ,现从袋中每次任取⼀个球,每次取出后不放回,连续取
两次,求两个⼩球所标数字之和为3的倍数的概率;
(2)若从中摸出⼀个球,观察颜⾊后放回,再摸出⼀个球,求两球颜⾊恰好不同的概率.
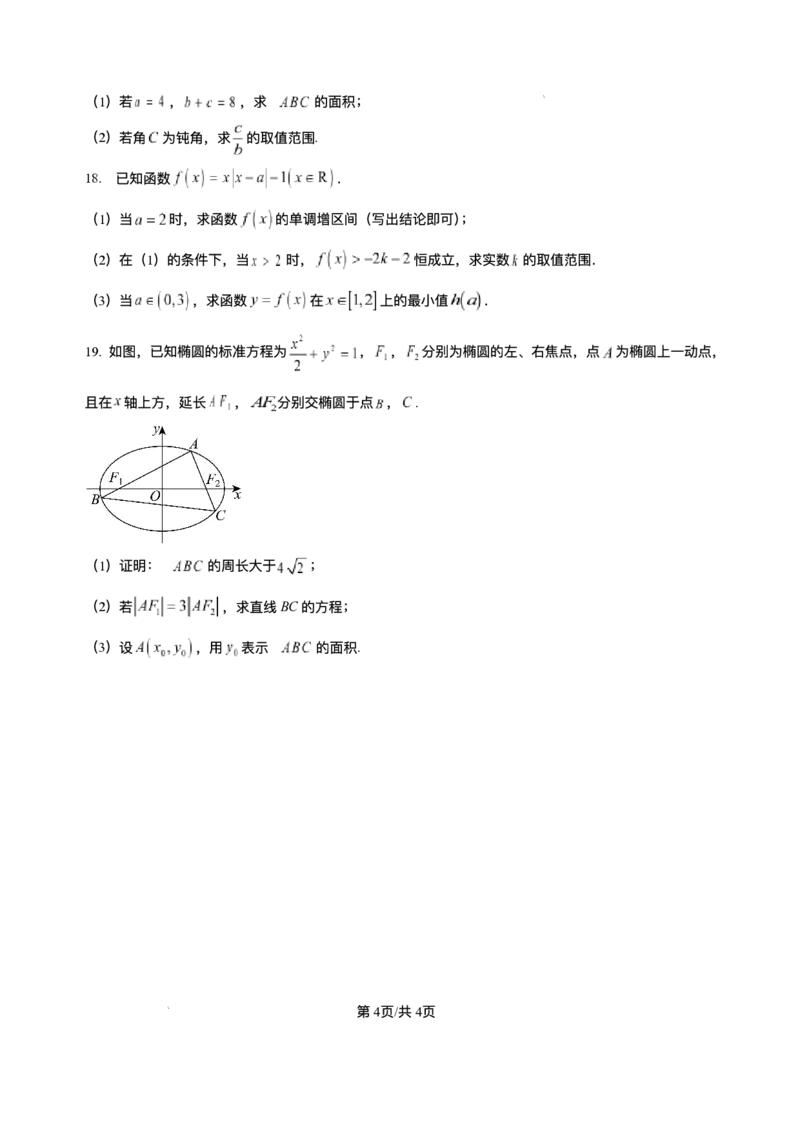
16. 如图1,在直⻆梯形 中, , ,且 ,现以 为⼀边向
梯形外作正⽅形 ,然后沿边 将正⽅形 折叠,使 , 为 中点,如图2.
(1)求证: 平⾯ ;
(2)求证:平⾯ 平⾯ ;
(3)求点 到平⾯ 的距离.
17. 的内⻆ , , 的对边分别为 , , ,已知 .
第3⻚/共4⻚
学科⽹(北京)股份有限公司(1)若 , ,求 的⾯积;
(2)若⻆ 为钝⻆,求 的取值范围.
18. 已知函数 .
(1)当 时,求函数 的单调增区间(写出结论即可);
(2)在(1)的条件下,当 时, 恒成⽴,求实数 的取值范围.
(3)当 ,求函数 在 上的最⼩值 .
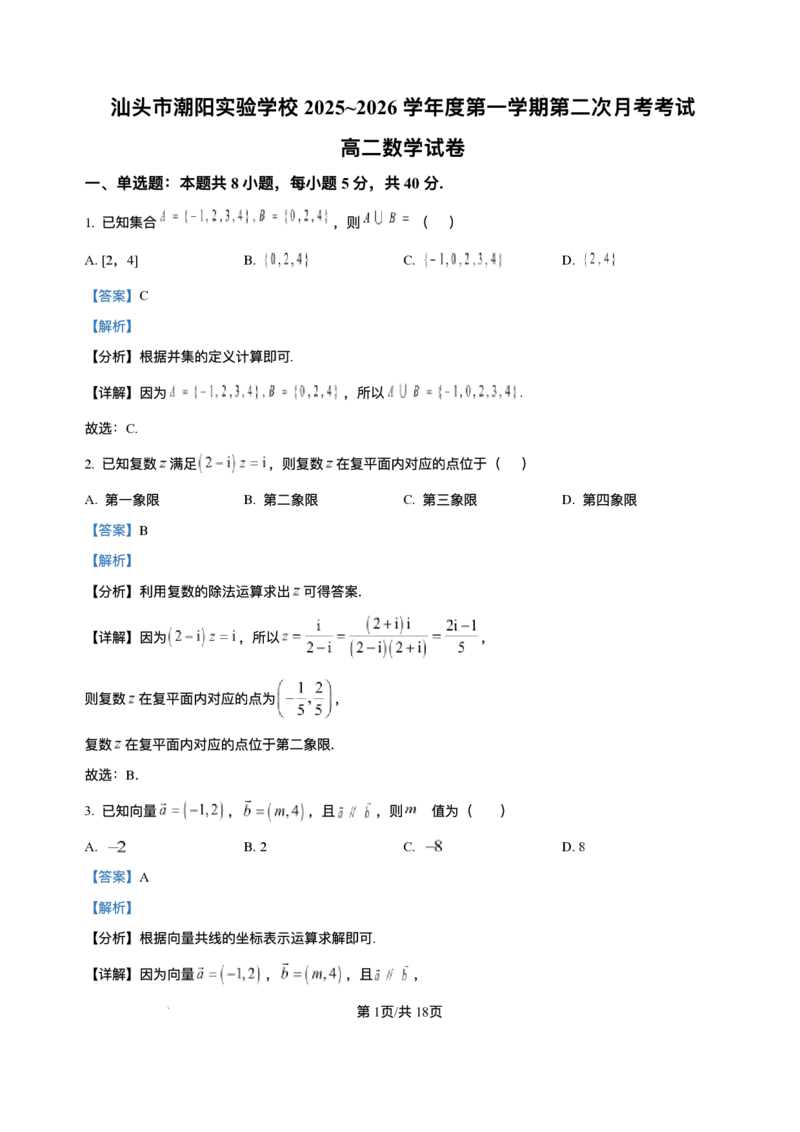
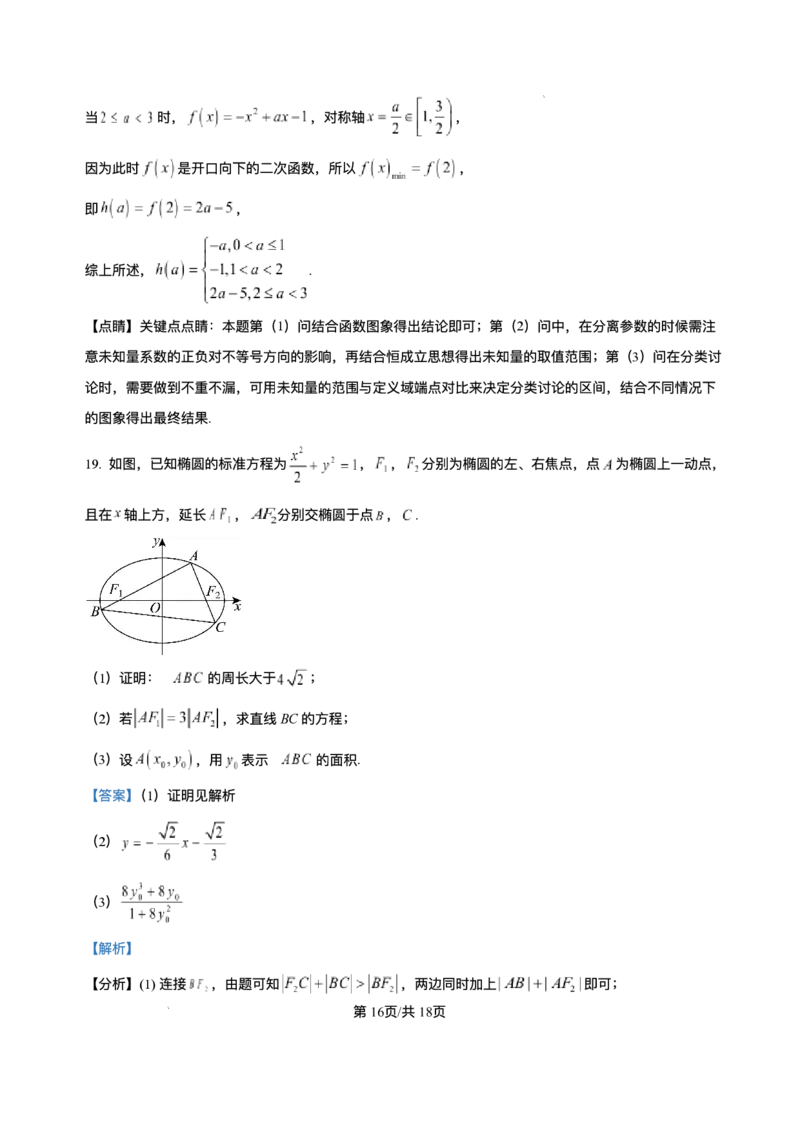
19. 如图,已知椭圆的标准⽅程为 , , 分别为椭圆的左、右焦点,点 为椭圆上⼀动点,
且在 轴上⽅,延⻓ , 分别交椭圆于点 , .
(1)证明: 的周⻓⼤于 ;
(2)若 ,求直线BC的⽅程;
(3)设 ,⽤ 表示 的⾯积.
第4⻚/共4⻚
学科⽹(北京)股份有限公司汕头市潮阳实验学校 学年度第⼀学期第⼆次⽉考考试
2025~2026
⾼⼆数学试卷
⼀、单选题:本题共8⼩题,每⼩题5分,共40分.
1. 已知集合 ,则 ( )
A.[2,4] B. C. D.
【答案】C
【解析】
【分析】根据并集的定义计算即可.
【详解】因为 ,所以 .
故选:C.
2. 已知复数 满⾜ ,则复数 在复平⾯内对应的点位于( )
A. 第⼀象限 B. 第⼆象限 C. 第三象限 D. 第四象限
【答案】B
【解析】
【分析】利⽤复数的除法运算求出 可得答案.
【详解】因为 ,所以 ,
则复数 在复平⾯内对应的点为 ,
复数 在复平⾯内对应的点位于第⼆象限.
故选:B.
3. 已知向量 , ,且 ,则 值为( )
A. B.2 C. D.8
【答案】A
【解析】
【分析】根据向量共线的坐标表示运算求解即可.
【详解】因为向量 , ,且 ,
第1⻚/共18⻚
学科⽹(北京)股份有限公司则 ,解得 ,
所以 的值为 .
故选:A.
4. 已知等差数列 的公差为1, ,则 ( )
A. B. C. D.
【答案】C
【解析】
【分析】根据已知关系,应⽤等差数列的通项公式求基本量,再写出通项公式.
【详解】若数列公差为 ,因为 ,所以 ,
⼜ ,解得 ,所以 .
故选:C
5. 若 ,则( )
A. B. C. D.
【答案】D
【解析】
【分析】利⽤指数函数单调性即可⽐较得出三个数的⼤⼩.
【详解】由函数 在 上为单调递增函数,可知 ,即 ;
⼜函数 在 上为单调递减函数,可知 ,即 ;
所以可得 .
故选:D
6. 已知 ,则 ( )
A. B. C. D.
【答案】C
【解析】
【分析】代⼊⼆倍⻆公式,以及诱导公式,即可求解.
第2⻚/共18⻚
学科⽹(北京)股份有限公司【详解】由条件可知, ,
⽽ .
故选:C
7. 已知过球⾯上 三点的截⾯和球⼼的距离等于球半径的⼀半,且 ,则球⾯积是
A. B. C. D.
【答案】C
【解析】
【详解】∵ D是正△ABC的中⼼,∴ AD是△ABC的外接圆半径.
∵ AD= ,
⼜OD= = OA,OA =OD +AD ,∴ R = ,
∴ R = ,∴ 球的表⾯积S=4πR = .
故选C
8. 吹奏乐器“埙”(如图1)在古代通常是⽤陶⼟烧制的,⼀种“埙”的外轮廓的上部是半椭圆,下部是半圆,
已知半椭圆 ( 且为常数)和半圆 组成的曲线C如图2所
示,曲线C交x轴的负半轴于点A,交y轴的正半轴于点G,点M是半圆上任意⼀点,当点M的坐标为
时, 的⾯积最⼤,则半椭圆的⽅程是( )
A. B.
第3⻚/共18⻚
学科⽹(北京)股份有限公司C. D.
【答案】D
【解析】
【分析】由点 在半圆上,可求 ,再根据已知 的⾯积最⼤的条件可知, ,
即 ,代⼊可求 ,进⽽可求椭圆⽅程
【详解】由点 在半圆上,所以 ,
由椭圆可知图中 ,
要使 的⾯积最⼤,可平⾏移动AG,当AG与半圆相切于 时,
M到直线AG的距离最⼤, 此时 ,即 ,
⼜
,
所以半椭圆的⽅程为
故选:D.
⼆、选择题:本题共3⼩题,每⼩题6分,共18分.在每⼩题给出的选项中,有多项符合题⽬
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
第4⻚/共18⻚
学科⽹(北京)股份有限公司9. 已知⼀组数据8,9,12,12,13,16,16,16,18,20,则这组数据的( )
A. 众数为12 B. 平均数为14 C. 中位数为14.5 D. 第25百分位数为12
【答案】BCD
【解析】
【分析】根据众数、平均数、中位数、百分位数的定义和计算公式⼀⼀计算即可.
【详解】对A,由题意可知,16出现的次数最多,则众数应为16,故A错误;
对B,平均数为 ,故B正确;
对C,中间两个数为13和16,则中位数为: ,故C正确;
对D, ,所以第25百分位数是从⼩到⼤排列后第三个数字,即为12,故D正确.
故选:BCD.
10. 如图,在正三棱柱 中, 为棱 的中点, ,则下列结论正确的是( )
A. B. 直线 与⾯ 所成⻆为
C 线段 D. 直线 ⾯
【答案】ABD
【解析】
【分析】对于A,利⽤线⾯垂直的判定定理与性质定理即可得证;对于B,利⽤线⾯⻆的定义即可得解;对
于C,正 中求解即可;对于D,利⽤线⾯平⾏的判定理证得即可.
【详解】对于A,因为在正三棱柱 中, ⾯ ,⽽ ⾯ ,所以
,
因为底⾯ 是正三⻆形, 为棱 的中点,所以 ,
⼜ ⾯ ,所以 ⾯ ,
因为 ⾯ ,所以 ,故A正确;
对于B,因为在正三棱柱 中, ⾯ ,所以 为直线 与⾯ 所成⻆,
第5⻚/共18⻚
学科⽹(北京)股份有限公司因为 ⾯ ,所以 ,⼜ ,
所以 ,则 ,故B正确;
对于C,在正 中, ,则 ,
所以 ,故C错误;
对于D,记 的中点为 ,连接 ,如图,
因为 是 的中点,⼜易知四边形 是平⾏四边形,所以 ,
因为 ,所以 ,所以四边形 是平⾏四边形,则
,
⼜ ⾯ , ⾯ ,所以直线 ⾯ ,故D正确.
故选:ABD.
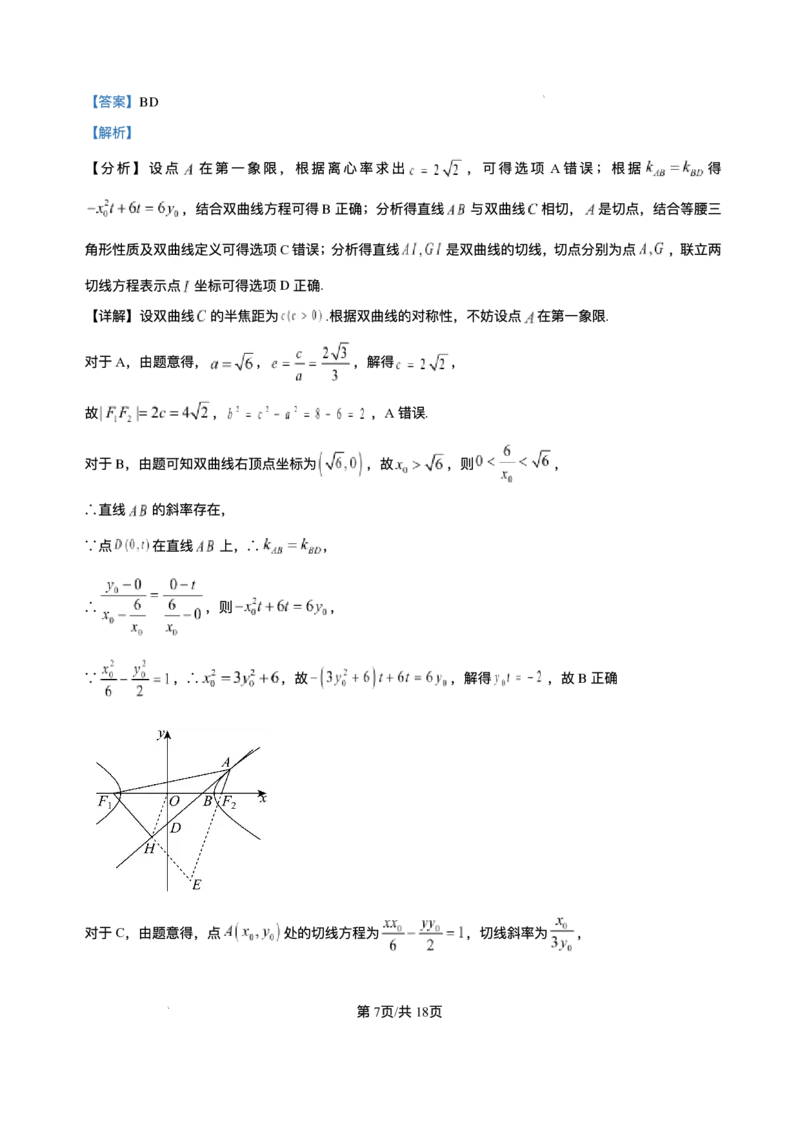
11. 双曲线的光学性质:从双曲线的⼀个焦点发出的光线,经双曲线反射后,反射光线的反向延⻓线经过双
曲线的另⼀个焦点.已知双曲线 : 的离⼼率为 ,左、右焦点分别为 , .点
在 上,点 ,点 在直线AB上,则下列说法正确的是( )
附:双曲线 ( , )在其上⼀点 处的切线⽅程为 .
A.
B.
C. 作 于点 ,则 ( 为坐标原点)
D. 若 的延⻓线交 于点 ,则 的内⼼在定直线上
第6⻚/共18⻚
学科⽹(北京)股份有限公司【答案】BD
【解析】
【分析】设点 在第⼀象限,根据离⼼率求出 ,可得选项 A错误;根据 得
,结合双曲线⽅程可得B正确;分析得直线 与双曲线 相切, 是切点,结合等腰三
⻆形性质及双曲线定义可得选项C错误;分析得直线 是双曲线的切线,切点分别为点 ,联⽴两
切线⽅程表示点 坐标可得选项D正确.
【详解】设双曲线 的半焦距为 .根据双曲线的对称性,不妨设点 在第⼀象限.
对于A,由题意得, , ,解得 ,
故 , ,A错误.
对于B,由题可知双曲线右顶点坐标为 ,故 ,则 ,
∴直线 的斜率存在,
∵点 在直线 上,∴ ,
∴ ,则 ,
∵ ,∴ ,故 ,解得 ,故B正确
对于C,由题意得,点 处的切线⽅程为 ,切线斜率为 ,
第7⻚/共18⻚
学科⽹(北京)股份有限公司∵ ,故直线 与双曲线 相切, 是切点.
由双曲线的光学性质可知,双曲线上任意⼀点处的切线平分该点与两焦点连线的夹⻆,
则 平分 ,延⻓ ,与 的延⻓线交于点 ,连接 ,
则 为等腰三⻆形, ,
∵ 为 的中点, 为 的中点,
∴ ,故C错误.
对于D,记 的内⼼为 ,则 是 的平分线, 是 的平分线,
由选项C可得,直线 是双曲线的切线,切点分别为点 ,设 ,
则直线 的⽅程为 ,直线 的⽅程为 ,
联⽴两式,解得 ,
由 得, ,设直线 ,
则 式可化为 ,即点 在定直线 上,故D正确.
故选:BD.
三、填空题:本题共3⼩题,每⼩题5分,共15分.
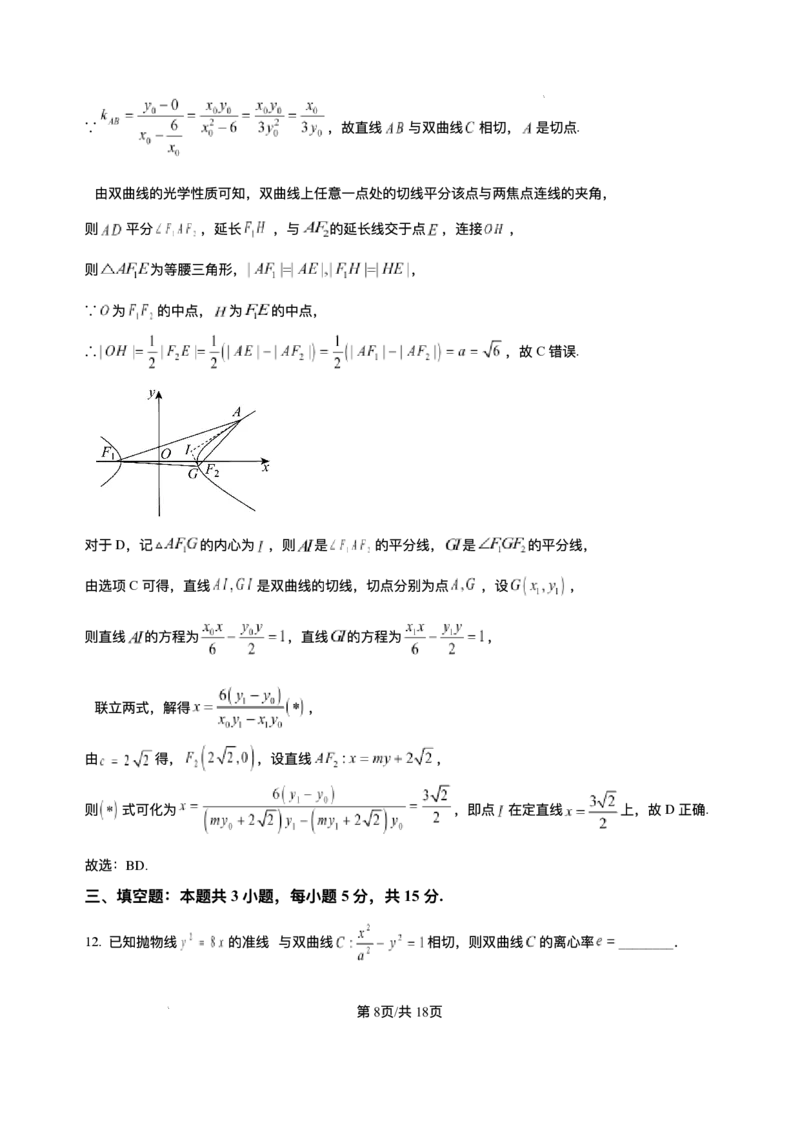
12. 已知抛物线 的准线 与双曲线 相切,则双曲线 的离⼼率 ________.
第8⻚/共18⻚
学科⽹(北京)股份有限公司【答案】 ;
【解析】
【详解】抛物线 的准线 ,
依题意可得,直线 经过双曲线 的左顶点,
则 ,所以 ,
故
13. 已知圆⼼为 ,直线 与圆 相切于点 ,则圆 的半径⻓为_____.
【答案】
【解析】
【分析】由题可得直线 斜率为2,则 ,建⽴⽅程可求得 ,进⽽求解即可.
【详解】由题意,直线 的斜率为2,
则 ,解得 ,即 ,
则圆 的半径⻓为 .
故答案为: .
14. 在斜 中, 为锐⻆,且满⾜ ,则 的最⼩值为
______.
【答案】
【解析】
【分析】将已知变形为 ,⽤两⻆和(差)的正弦公式得到
,进⽽得到 与 的关系,代⼊ ⽤基本不等式
即可求最⼩值.
第9⻚/共18⻚
学科⽹(北京)股份有限公司【详解】 ,
∴
∴ ,
∴ ,
∴ ,
⼜∵ ,∴ ,
∴ ,
∵ 为锐⻆,∴
∴
,
当且仅当 ,即 时等号成⽴.
故答案为:
【点睛】⽅法点睛:本题关键是化“ 弦” 为“ 切” ,通过代⼊减元运⽤基本不等式求和的最⼩值.
四、解答题:本题共5⼩题,共77分.解答应写出⽂字说明、证明过程或演算步骤.
15. 袋⼦中有5个⼤⼩质地完全相同的球,其中2个红球,3个⻩球.
(1)若这5个球分别标有数字 , , , , ,现从袋中每次任取⼀个球,每次取出后不放回,连续取
两次,求两个⼩球所标数字之和为3的倍数的概率;
(2)若从中摸出⼀个球,观察颜⾊后放回,再摸出⼀个球,求两球颜⾊恰好不同的概率.
【答案】(1)
(2)
【解析】
第10⻚/共18⻚
学科⽹(北京)股份有限公司【分析】(1)根据不放回的随机抽样问题,列出样本空间,利⽤古典概型求概率即可;
(2)根据有放回的随机抽样问题,列出样本空间,利⽤古典概型求概率即可;
【⼩问1详解】
不放回连续取两次的样本空间 , , , , ,
, , , , , , , , , , ,
, , ,
记“ 两数之和为3的倍数” 为事件 ,则事件 , , , , ,
, ,
【⼩问2详解】
设5个球记为 , , , , ,则有放回地取出两个的样本空间
, , , , , , ,
, , , , , , , ,
, , , , , , , ,
记“ 两球颜⾊恰好不同的概率” 为事件 ,则 , , ,
, , , , , , , ,
,
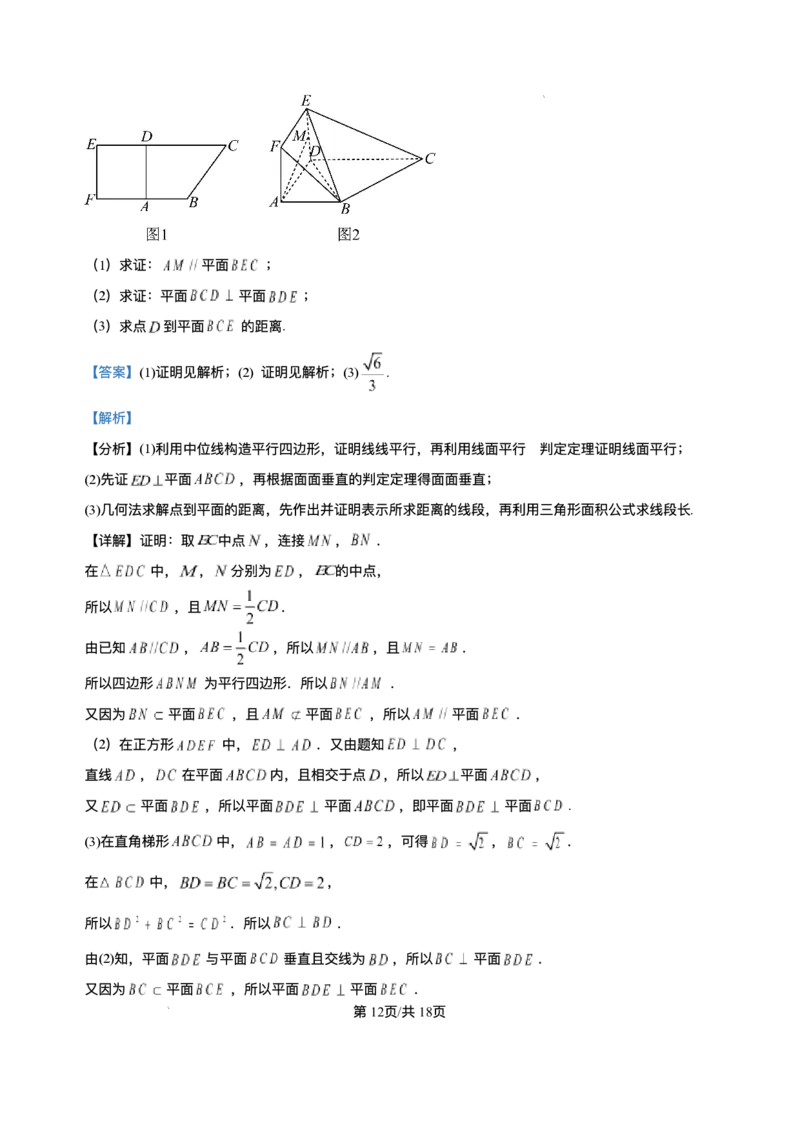
16. 如图1,在直⻆梯形 中, , ,且 ,现以 为⼀边向
梯形外作正⽅形 ,然后沿边 将正⽅形 折叠,使 , 为 的中点,如图2.
第11⻚/共18⻚
学科⽹(北京)股份有限公司(1)求证: 平⾯ ;
(2)求证:平⾯ 平⾯ ;
(3)求点 到平⾯ 的距离.
【答案】(1)证明⻅解析;(2) 证明⻅解析;(3) .
【解析】
【分析】(1)利⽤中位线构造平⾏四边形,证明线线平⾏,再利⽤线⾯平⾏ 判定定理证明线⾯平⾏;
(2)先证 平⾯ ,再根据⾯⾯垂直的判定定理得⾯⾯垂直;
(3)⼏何法求解点到平⾯的距离,先作出并证明表示所求距离的线段,再利⽤三⻆形⾯积公式求线段⻓.
【详解】证明:取 中点 ,连接 , .
在 中, , 分别为 , 的中点,
所以 ,且 .
由已知 , ,所以 ,且 .
所以四边形 为平⾏四边形.所以 .
⼜因为 平⾯ ,且 平⾯ ,所以 平⾯ .
(2)在正⽅形 中, .⼜由题知 ,
直线 , 在平⾯ 内,且相交于点 ,所以 平⾯ ,
⼜ 平⾯ ,所以平⾯ 平⾯ ,即平⾯ 平⾯ .
(3)在直⻆梯形 中, , ,可得 , .
在 中, ,
所以 .所以 .
由(2)知,平⾯ 与平⾯ 垂直且交线为 ,所以 平⾯ .
⼜因为 平⾯ ,所以平⾯ 平⾯ .
第12⻚/共18⻚
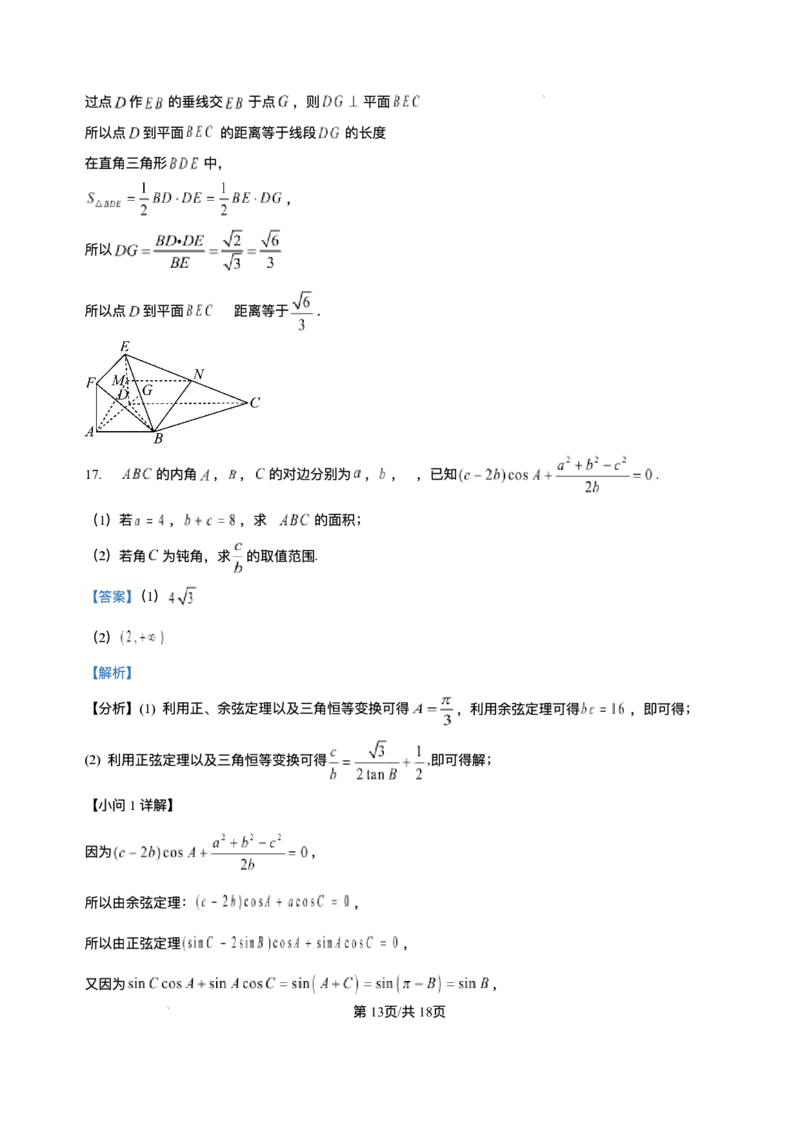
学科⽹(北京)股份有限公司过点 作 的垂线交 于点 ,则 平⾯
所以点 到平⾯ 的距离等于线段 的⻓度
在直⻆三⻆形 中,
,
所以
所以点 到平⾯ 距离等于 .
17. 的内⻆ , , 的对边分别为 , , ,已知 .
(1)若 , ,求 的⾯积;
(2)若⻆ 为钝⻆,求 的取值范围.
【答案】(1)
(2)
【解析】
【分析】(1) 利⽤正、余弦定理以及三⻆恒等变换可得 ,利⽤余弦定理可得 ,即可得;
(2) 利⽤正弦定理以及三⻆恒等变换可得 ,即可得解;
【⼩问1详解】
因为 ,
所以由余弦定理: ,
所以由正弦定理 ,
⼜因为 ,
第13⻚/共18⻚
学科⽹(北京)股份有限公司所以 ,因为 ,所以 ,
因为 ,所以 ,
由余弦定理 ,
因为 , ,所以 ,所以 ,
所以 的⾯积 .
【⼩问2详解】
因为⻆ 为钝⻆,所以 ,所以 ,
因为 ,所以 ,
代⼊ 得 ,
因为 ,所以 ,即 ,
所以 的取值范围为 .
18. 已知函数 .
(1)当 时,求函数 的单调增区间(写出结论即可);
(2)在(1)的条件下,当 时, 恒成⽴,求实数 的取值范围.
(3)当 ,求函数 在 上的最⼩值 .
【答案】(1) ,
(2)
第14⻚/共18⻚
学科⽹(北京)股份有限公司(3)
【解析】
【分析】(1)将函数解析式表示为分段函数的形式,即可写出函数的单调递增区间;
(2)结合已知分离参数得 在 上恒成⽴,即可得到 的取值范围;
(3)对实数 的范围进⾏分类讨论,分析函数 在 上的单调性与最值,进⽽得到 的表达式.
【⼩问1详解】
当 时, ,
所以函数 的单调增区间为 ,
【⼩问2详解】
当 时, ,
化为 ,
即 在 上恒成⽴,
因为函数 在 上单调递减,
所以 ,所以 ,
即 的取值范围为 ;
【⼩问3详解】
当 时, ,对称轴 ,
所以函数 在 上单调递增, ;
当 时, ,对称轴 ,
结合图象知, 在 上单调递减,在 上单调递增,
所以 ;
第15⻚/共18⻚
学科⽹(北京)股份有限公司当 时, ,对称轴 ,
因为此时 是开⼝向下的⼆次函数,所以 ,
即 ,
综上所述, .
【点睛】关键点点睛:本题第(1)问结合函数图象得出结论即可;第(2)问中,在分离参数的时候需注
意未知量系数的正负对不等号⽅向的影响,再结合恒成⽴思想得出未知量的取值范围;第(3)问在分类讨
论时,需要做到不重不漏,可⽤未知量的范围与定义域端点对⽐来决定分类讨论的区间,结合不同情况下
的图象得出最终结果.
19. 如图,已知椭圆的标准⽅程为 , , 分别为椭圆的左、右焦点,点 为椭圆上⼀动点,
且在 轴上⽅,延⻓ , 分别交椭圆于点 , .
(1)证明: 的周⻓⼤于 ;
(2)若 ,求直线BC的⽅程;
(3)设 ,⽤ 表示 的⾯积.
【答案】(1)证明⻅解析
(2)
(3)
【解析】
【分析】(1)连接 ,由题可知 ,两边同时加上 即可;
第16⻚/共18⻚
学科⽹(北京)股份有限公司(2)设 , , ,由椭圆的定义和两点间距离公式计算得出 ,联⽴
,求得 , ,根据两点求出直线 的⽅程;
(3)联⽴ 和 ⽅程,利⽤⻙达定理得出 和 ,再利⽤
⾯积⽐求出即可.
【⼩问1详解】
连接 ,注意到 ,
故 的周⻓为 .
【⼩问2详解】
设 , , ,
由 ,且 ,故 ,
⼜ ,则 ,即 ,
因此 ,故直线 的⽅程为: ,即 ,
直线 的⽅程为: ,联⽴ ,得 ,
则 ,即 ,因此 ,
⽽ ,因此 ,
故直线 的⽅程为: ,即 .
【⼩问3详解】
第17⻚/共18⻚
学科⽹(北京)股份有限公司因为点A在x轴上⽅,所以直线 斜率不为0,
设直线 ,直线 , , , , ,
联⽴ ,可得 ,则 ,
注意到 ,故 .
联⽴ ,可得 ,则 ,
注意到 ,故 .
则 , .
注意到 ,因为 , ,
所以 ,
则
.
第18⻚/共18⻚
学科⽹(北京)股份有限公司