数学-山东济宁一中2024年高二上学期10月月考_2024-2025高二（7-7月题库）_2024年10月试卷_1012山东济宁一中2024年高二上学期10月月考

济宁市第一中学 2024-2025 学年度第一学期
高二阶段性测试
数学试卷
2024.10
注意事项：
1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.满分150分.考试用时120分
钟.
2．答卷前，考生务必将自己的姓名、准考证号填涂在答题卡规定的地方.
一、单选题：本题共8小题，每小题5分，共40分.在每小题给出的选项中，只有一项是符
合题目要求的
1．已知A0,1,1，B1,1,4，平面的法向量为2,t,6，若AB//，则t （ ）
A．10 B．3 C．4 D．5
      
2．如图，G是ABC的重心，OAa,OBb,OC c，则OG（ ）
1 2 2 2  2  1 
A． a b c B． a b c
3 3 3 3 3 3
2 2 2 1 1 1
C． a b c D． a b c
3 3 3 3 3 3
  r r  
3．已知向量a2,1,2，b4,2,x，
a//b
，则 ab （ ）
A．3 B．9 C．27 D．81
4．已知事件A，B是互斥事件，PA 1 ，P  B   2 ，则PAB（ ）
6 3
1 4 1 2
A． B． C． D．
18 9 2 3
5．已知点D在VABC确定的平面内，O是平面ABC外任意一点，若正实数x,y满足
    2xy
ODxOA2yOBOC ，则 的最小值为（ ）
xy
5 9
A． B． C．2 D．4
2 2
试卷第1页，共4页
{#{QQABTQKAggiIAJAAAQgCAwFoCEGQkBGAAYgORBAEsAAASBNABCA=}#}6. 已知a   2,1,3  ，b  1,4,2 ，c   7,5, ，若a  ，b  ，c  三向量不能构成空间
向量的一组基底，则实数的值为（ ）
65
A.0 B.5 C.9 D.
7
7．已知正三棱柱ABCABC 的侧面积是两底面积的6 3倍，点E为四边形ABBA 的中心，
1 1 1 1 1
点F为棱CC 的中点，则异面直线BF与CE所成角的余弦值为（ ）
1
2 39 39 39 3 39
A． B． C． D．
13 13 26 26
8．依次抛掷两枚质地均匀的骰子，记骰子向上的点数．用x表示第一次抛掷骰子的点数，
用y表示第二次抛掷骰子的点数，用x,y表示一次试验的结果．记“x y7”为事件A，
“xy2k1
 kN*
”为事件B，“x3”为事件C，则 （ ）
A．A与B相互独立 B．A与B对立
C．B与C相互独立 D．A与C相互独立
二、多选题：本题共3小题，共18分。在每小题给出的选项中，有多项符合题目要求.全选
对得6分，部分选对得部分分，有选错的得0分
9．下述关于频率与概率的说法中，错误的是（ ）
A．设有一大批产品，已知其次品率为0.1，则从中任取100件，必有10件是次品
B．利用随机事件发生的频率估计随机事件的概率，即使随机试验的次数超过10000，所
估计出的概率也不一定很准确．
C．随机事件发生的频率就是这个随机事件发生的概率
3
D．做7次抛硬币的试验，结果3次出现正面，因此，抛一枚硬币出现正面的概率是
7
   π
10．设空间两个单位向量OAm,n,0,OB0,n, p与向量OC 1,1,1的夹角都等于 ，则
4
cosAOB（ ）
2 3 1 3
A． B．
4 4
2 3 1 3
C． D．
4 4
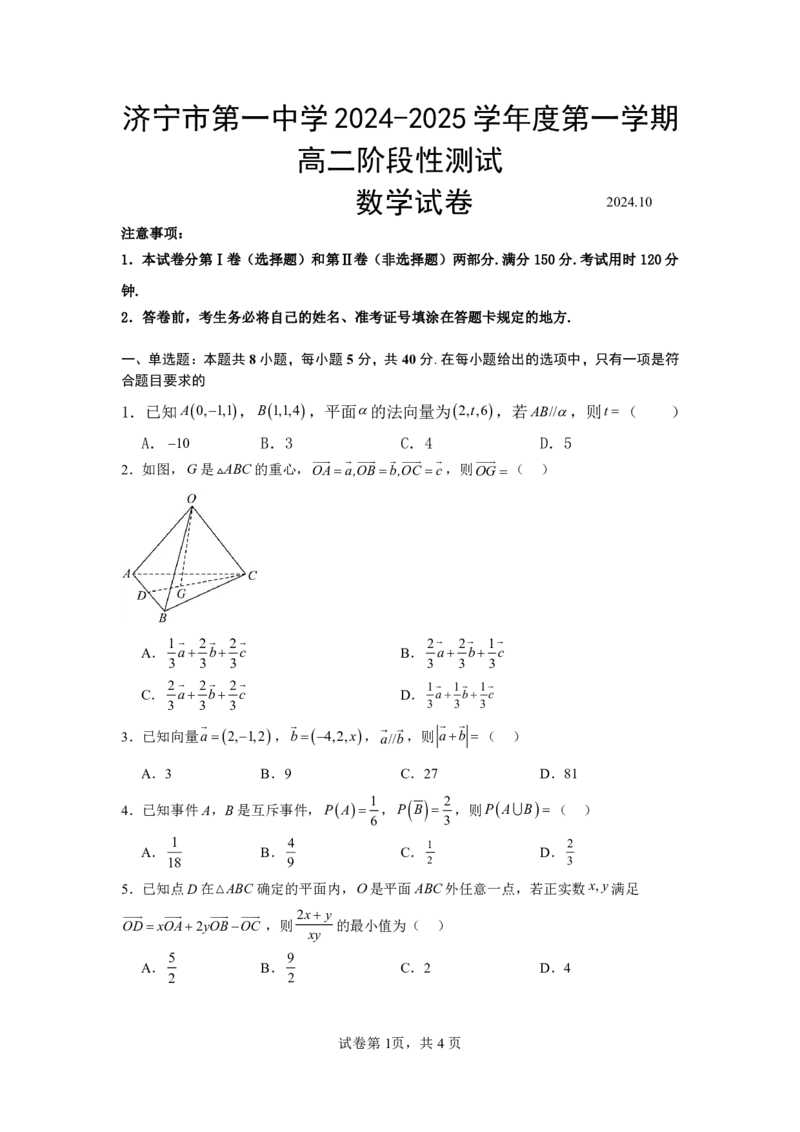
11．如图，在边长为1的正方体ABCD ABCD中，点E为线段DD 的中点，点F 为线段BB
1 1 1 1 1 1
的中点，则（ ）
试卷第2页，共4页
{#{QQABTQKAggiIAJAAAQgCAwFoCEGQkBGAAYgORBAEsAAASBNABCA=}#}5 30
A．点A到直线BE的距离为 B．直线FC 到直线AE的距离为
1 1 1
3 5
1 1
C．点A到平面ABE的距离为 D．直线FC 到平面ABE的距离为
1 1 3 1 1 3
第II 卷（非选择题）
三、填空题：本题共3小题，每小题5分，共15分.
12.在一次掷硬币试验中，掷100次，其中有48次正面朝上，设反面朝上为事件A，则事件
A出现的频率为 ．
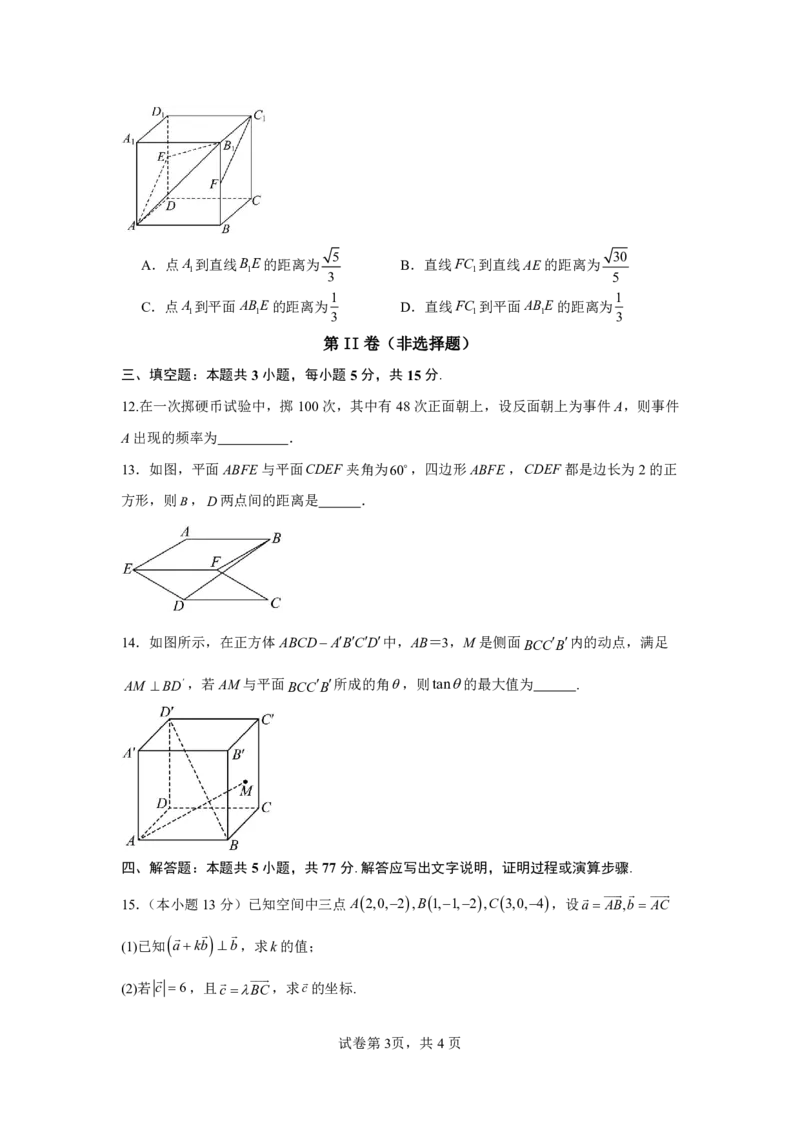
13．如图，平面ABFE与平面CDEF夹角为60，四边形ABFE，CDEF都是边长为2的正
方形，则B，D两点间的距离是 ．
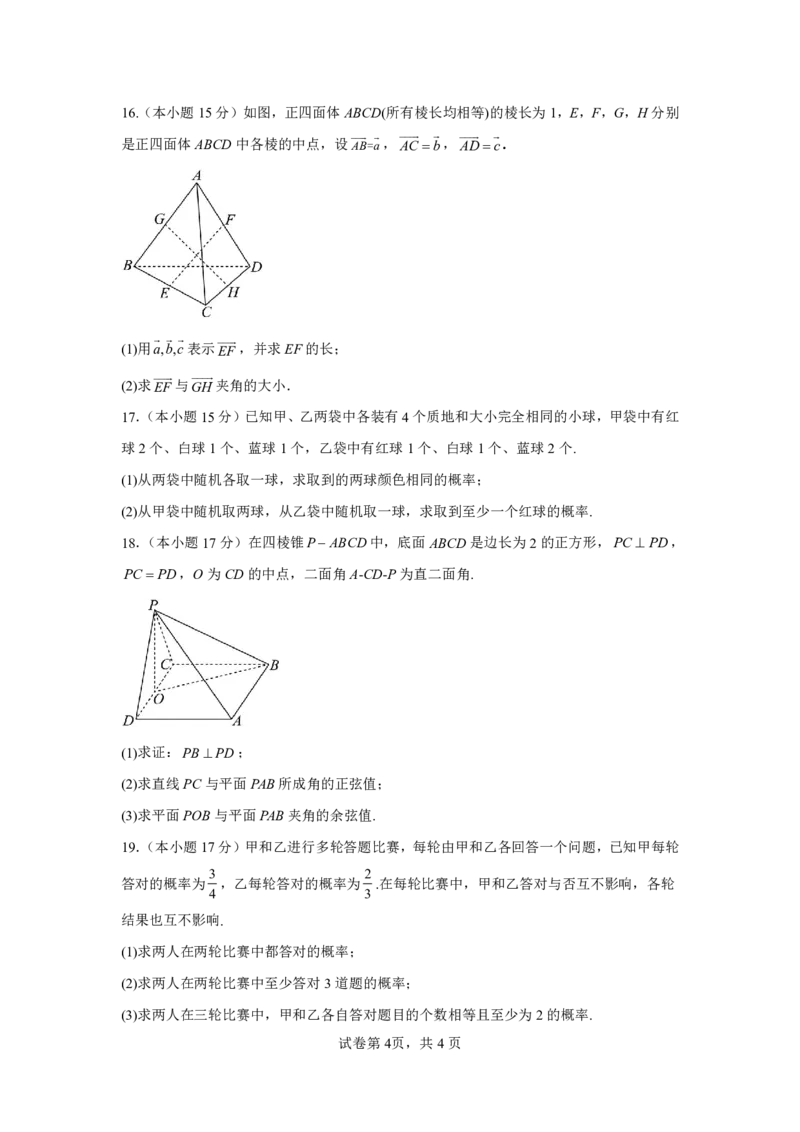
14．如图所示，在正方体ABCDABCD中，AB＝3，M是侧面
BCC

B
内的动点，满足
AM BD，若AM与平面 BCC  B 所成的角，则tan的最大值为 .
四、解答题：本题共5小题，共77分.解答应写出文字说明，证明过程或演算步骤.
15．（本小题13分）已知空间中三点A2,0,2,B1,1,2,C3,0,4，设a 


A

B

,b



A

C

   
(1)已知 akb b，求k的值；
(2)若 c  6，且c    B  C  ，求c  的坐标.
试卷第3页，共4页
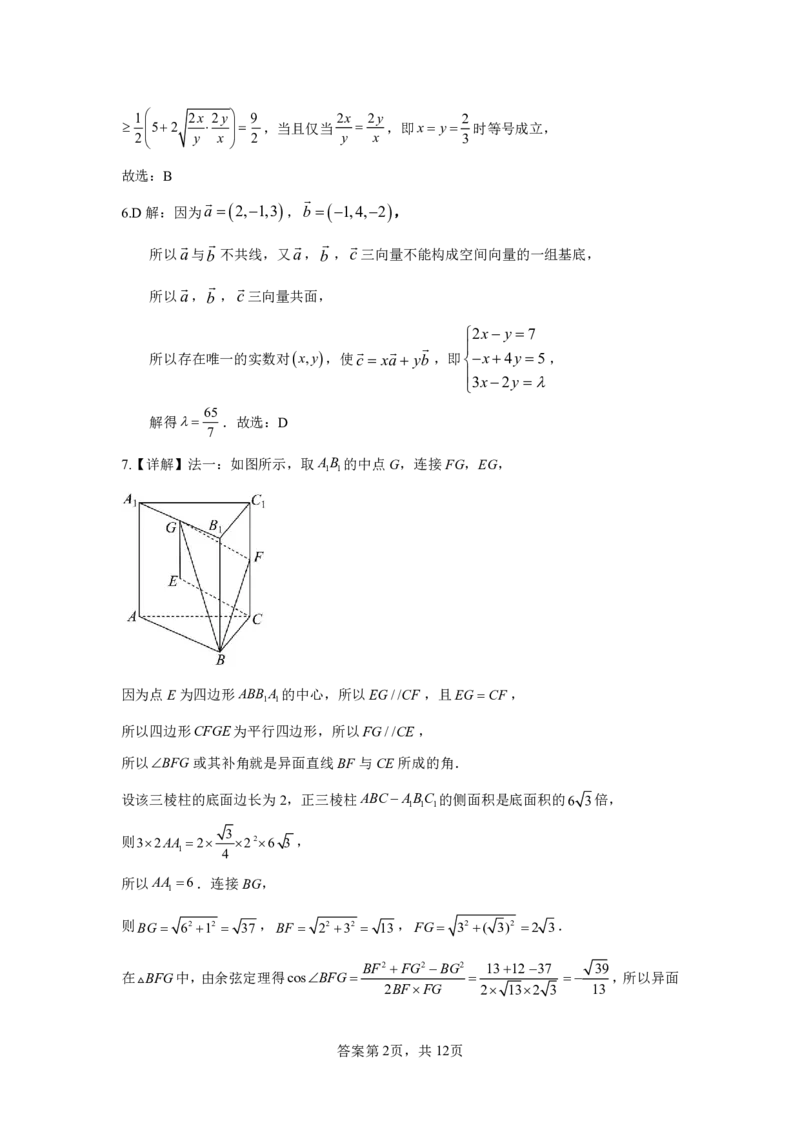
{#{QQABTQKAggiIAJAAAQgCAwFoCEGQkBGAAYgORBAEsAAASBNABCA=}#}16.（本小题15分）如图，正四面体ABCD(所有棱长均相等)的棱长为1，E，F，G，H分别
     
是正四面体ABCD中各棱的中点，设 AB=a ，ACb，ADc.
   
(1)用a,b,c表示
EF
，并求EF的长；
 
(2)求
EF
与GH夹角的大小．
17．（本小题15分）已知甲、乙两袋中各装有4个质地和大小完全相同的小球，甲袋中有红
球2个、白球1个、蓝球1个，乙袋中有红球1个、白球1个、蓝球2个.
(1)从两袋中随机各取一球，求取到的两球颜色相同的概率；
(2)从甲袋中随机取两球，从乙袋中随机取一球，求取到至少一个红球的概率.
18．（本小题17分）在四棱锥PABCD中，底面ABCD是边长为2的正方形，PCPD，
PCPD，O为CD的中点，二面角A-CD-P为直二面角.
(1)求证：PBPD；
(2)求直线PC与平面PAB所成角的正弦值；
(3)求平面POB与平面PAB夹角的余弦值.
19．（本小题17分）甲和乙进行多轮答题比赛，每轮由甲和乙各回答一个问题，已知甲每轮
3 2
答对的概率为 ，乙每轮答对的概率为 .在每轮比赛中，甲和乙答对与否互不影响，各轮
4 3
结果也互不影响.
(1)求两人在两轮比赛中都答对的概率；
(2)求两人在两轮比赛中至少答对3道题的概率；
(3)求两人在三轮比赛中，甲和乙各自答对题目的个数相等且至少为2的概率.
试卷第4页，共4页
{#{QQABTQKAggiIAJAAAQgCAwFoCEGQkBGAAYgORBAEsAAASBNABCA=}#}试卷第5页，共4页
{#{QQABTQKAggiIAJAAAQgCAwFoCEGQkBGAAYgORBAEsAAASBNABCA=}#}高二数学参考答案
1.【答案】A

【详解】因为AB1,2,3，AB//，
所以1,2,32,t,60，即22t180，解得t10.
故选：A.
2.【答案】D
     
【解析】G是ABC的重心，OAa,OBb,OC c，
    2
OGOCCG，CG CD，
3
 1         
CD CACB ，CAOAOC，CBOBOC，
2
  2 1    1 1 1
OGOC  CACB  OC OB OA，
3 2 3 3 3
 1 1 1
OG a b c．
3 3 3
故选：D．
3．A
【详解】向量a  2,1,2，b  4,2,x且a  //b  ，
2 1 2 
则   ，解得x4，所以b 4,2,4，
4 2 x
所以a  b  2,1,2，
所以 a  b   2212 22 3.
故选：A.
4.【答案】C
【详解】∵PB1P  B  ，P  B   2 ，∴PB 1 ，
3 3
1 1 1
∵事件A，B是互斥事件，∴PABPA PB   ．故选：C
6 3 2
5．B
【详解】由A,B,C,D四点共面，可知x2y11，即x2y2，
2xy 2 1 1 2 1  1  2x 2y 
由x0,y0，    x 2y    5  
xy y x 2 y x  2 y x 
答案第1页，共12页
{#{QQABTQKAggiIAJAAAQgCAwFoCEGQkBGAAYgORBAEsAAASBNABCA=}#}1 2x 2y 9 2x 2y 2
 52   ，当且仅当  ，即x y 时等号成立，
 
2 y x  2 y x 3
故选：B
 
6.D解：因为a  2,1,3  ，b 1,4,2 ，
    
所以a与b 不共线，又a，b ，c三向量不能构成空间向量的一组基底，
  
所以a，b ，c三向量共面，
2x y 7
所以存在唯一的实数对x,y，使c   xa   yb  ，即  x4y 5，

3x2y 
65
解得 ．故选：D
7
7.【详解】法一：如图所示，取AB 的中点G，连接FG，EG，
1 1
因为点E为四边形ABBA 的中心，所以EG//CF ，且EG CF，
1 1
所以四边形CFGE为平行四边形，所以FG//CE，
所以BFG或其补角就是异面直线BF与CE所成的角．
设该三棱柱的底面边长为2，正三棱柱ABCABC 的侧面积是底面积的6 3倍，
1 1 1
3
则32AA 2 226 3 ，
1 4
所以AA 6．连接BG，
1
则 BG 6212  37 ， BF  2232  13 ，FG 32 ( 3)2 2 3．
BF2FG2BG2 131237 39
在BFG中，由余弦定理得cosBFG   ，所以异面
2BFFG 2 132 3 13
答案第2页，共12页
{#{QQABTQKAggiIAJAAAQgCAwFoCEGQkBGAAYgORBAEsAAASBNABCA=}#}39
直线BF与CE所成角的余弦值为 ，
13
3
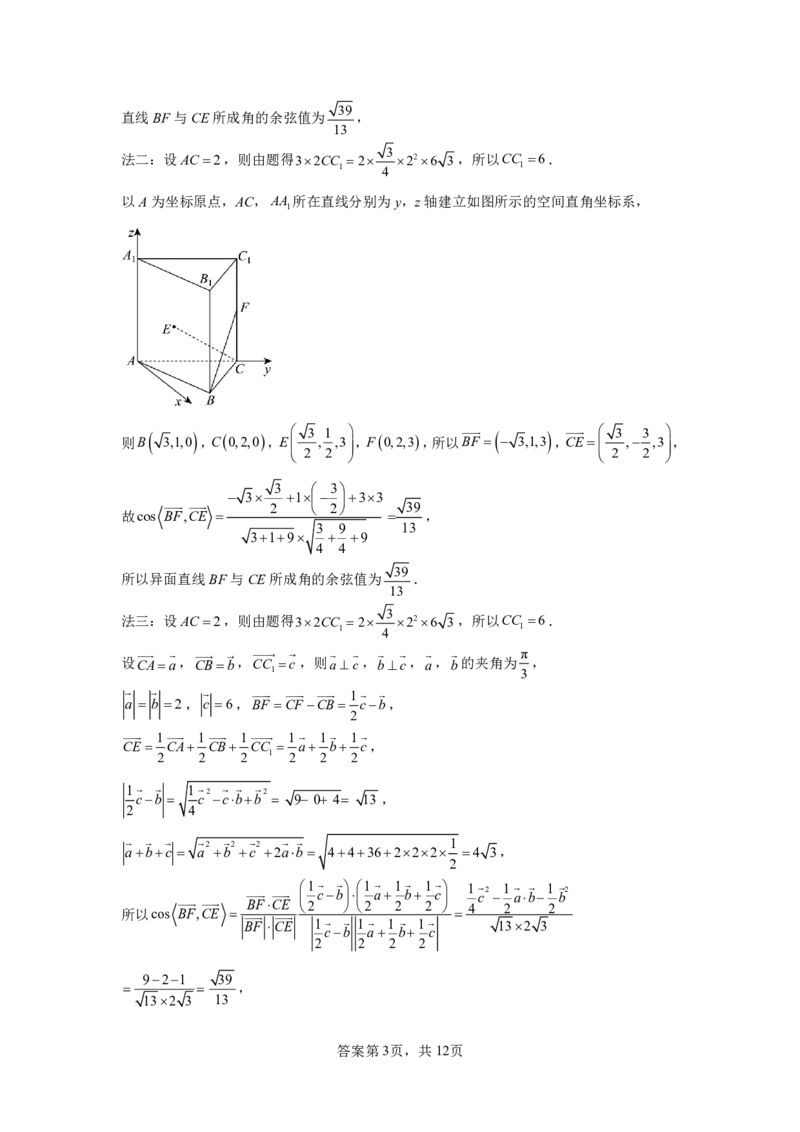
法二：设AC2，则由题得32CC 2 226 3，所以CC 6．
1 4 1
以A为坐标原点，AC，AA 所在直线分别为y，z轴建立如图所示的空间直角坐标系，
1
则B  3,1,0  ，C0,2,0，E   3 , 1 ,3  ，F0,2,3，所以  B  F     3,1,3  ，C  E     3 , 3 ,3  ，
   
 2 2   2 2 
3  3
 3 1 33
  2  2 39
故cos BF,CE   ，
3 9 13
319  9
4 4
39
所以异面直线BF与CE所成角的余弦值为 ．
13
3
法三：设AC2，则由题得32CC 2 226 3，所以CC 6．
1 4 1
  uur r uuur r       π
设CAa， CBb ，CC c，则ac，bc，a，b的夹角为 ，
1 3
      1 
a  b 2， c 6，BF CFCB cb，
2
 1 1 1 1 1 1
CE  CA CB CC  a b c，
2 2 2 1 2 2 2
1  1
2
  
2
cb  c cbb  9 0 4 13 ，
2 4
a  b  c   a  2 b  2 c  2 2a  b   4436222 1 4 3，
2
    1 c  b     1 a   1 b   1 c   1 c  2  1 a  b   1 b  2
  BFCE 2  2 2 2  4 2 2
所以cos BF,CE    
BF CE 1  1 1  1 132 3
cb a b c
2 2 2 2
921 39
  ，
132 3 13
答案第3页，共12页
{#{QQABTQKAggiIAJAAAQgCAwFoCEGQkBGAAYgORBAEsAAASBNABCA=}#}39
所以异面直线BF与CE所成角的余弦值为 .
13
故选：B．
8.【答案】D
【详解】依题意依次抛掷两枚质地均匀的骰子，基本事件总数为6636个；
其中事件A“ x y7 ”包含的样本点有：
1,6，2,5，3,4，4,3，5,2，6,1共6个；
事件 B “ xy2k1
 kN*
”，包含的样本点有：
1,1， 3,3 ，5,5 ，1,3 ，1,5，3,1，3,5，5,1，5,3共9个，
事件C “x3”，包含的样本点有：1,1，1,2，1,3，1,4，1,5，1,6，
2,1，2,2，2,3，2,4，2,5，2,6，
3,1，3,2，3,3，3,4，3,5，3,6共18个，
所以A与B不能同时发生，但是能同时不发生，故不是对立事件，故 B 错误；
因为A与B不能同时发生，所以A与B是互斥事件，则PAB0，
6 1 9 1
又PA  ，PB  ，所以PABPAPB，
66 6 66 4
所以A与B不相互独立，故A错误；
事件BC包含的样本点有：1,1， 3,3 ，1,3 ，1,5，3,1，3,5共6个，
1
因为PBC  PBPC，所以 B与 C不相互独立，故C错误．
6
又事件AC包含的样本点有： 1,6，2,5，3,4共3个，
1 1 3 1
所以PC ，PAPC ，则PAC  PAPC ，
2 12 36 12
所以A 与 C 相互独立，故D正确；
故选：D
9．ACD
【详解】对于A: 从中任取100件，可能有10件，A错误；
对于B:10000次的界定没有科学依据，“不一定很准确"的表达正确，试验次数越多，频率越
稳定在概率值附近，但并非试验次数越多，频率就等于概率，B正确.
答案第4页，共12页
{#{QQABTQKAggiIAJAAAQgCAwFoCEGQkBGAAYgORBAEsAAASBNABCA=}#}对于C:多次重复试验中事件发生的频率在某一常数附近，此常数为概率，与描述不符，C
错误；
3
对于D: 做7次抛硬币的试验，结果3次出现正面，因此，抛一枚硬币出现正面的频率是 ，
7
3
不是概率为 ，D错误；
7
故选:ACD.
10．AC
  
【详解】空间两个单位向量OAm,n,0，OB0,n,p与向量OC1,1,1的夹角都等于
π
，
4
 
AOC BOC  ， OC  3，
4
    6
OAOC OAOC cosAOC ，
2
  6
又 OAOCmn ，mn ，
2

又OA为单位向量，m2n2 1 ，
 2 3  2 3
 6 m2  m2 
mn  4  4
联立 2 ，得 或 ，
 m2n2 1  n2  2 3  n2  2 3
 
 4  4
 
OAm,n,0，OB0,n,p，
2 3
cosAOBn2 .
4
故选：AC.
11．ABD
 1  1
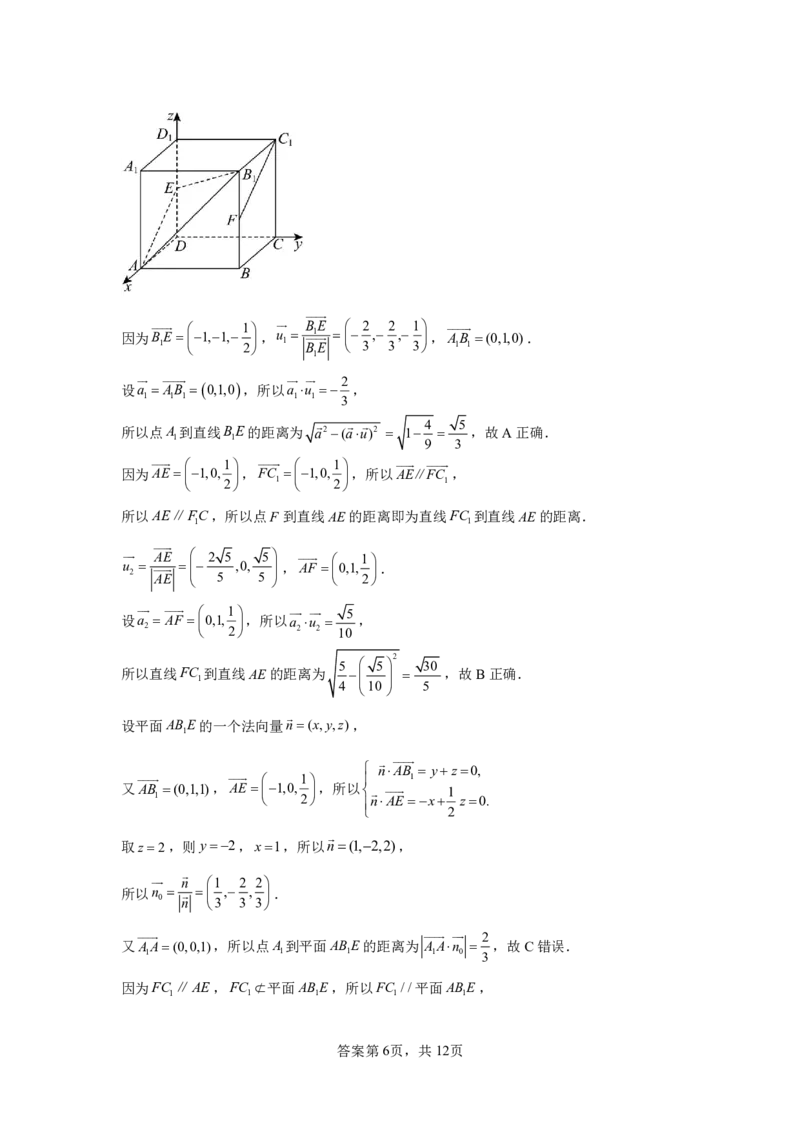
【详解】建立如图所示的空间直角坐标系，则A 1,0,1，B 1,1,1，E0,0, ，F1,1, ，
1 1  2  2
C 0,1,1， ．
1
1,0,0
答案第5页，共12页
{#{QQABTQKAggiIAJAAAQgCAwFoCEGQkBGAAYgORBAEsAAASBNABCA=}#}
  1  BE  2 2 1 
因为B 1 E   1,1, 2   ，u 1   B 1 E     3 , 3 , 3   ，A 1 B 1 (0,1,0)．
1
    2
设a  AB 0,1,0，所以a u  ，
1 1 1 1 1 3
   4 5
所以点A到直线BE的距离为 a2(au)2  1  ，故A正确．
1 1
9 3
  1   1  
因为AE 1,0, ，FC 1,0, ，所以AE∥FC ，
 2 1  2 1
所以AE∥FC，所以点F 到直线AE的距离即为直线FC 到直线AE的距离．
1 1

 AE  2 5 5   1
u 2   A  E      5 ,0, 5    ，AF   0,1, 2   ．
   1   5
设a  AF 0,1, ，所以a u  ，
2  2 2 2 10
2
5  5 30
所以直线FC 到直线AE的距离为    ，故B正确．
1  
4 10  5

设平面ABE的一个法向量n(x,y,z)，
1
 
 nAB  yz0,
   1  1
又AB 1 (0,1,1)，AE   1,0, 2   ，所以 n    A  E  x 1 z0.
 2

取z2，则y2，x1，所以n(1,2,2)，

 n 1 2 2
所以n    , , ．
0 n 3 3 3
   2
又AA(0,0,1)，所以点A到平面ABE的距离为 AAn  ，故C错误．
1 1 1 1 0 3
因为FC ∥AE，FC  平面ABE，所以FC //平面ABE，
1 1 1 1 1
答案第6页，共12页
{#{QQABTQKAggiIAJAAAQgCAwFoCEGQkBGAAYgORBAEsAAASBNABCA=}#}所以FC 到平面ABE的距离即为点F 到平面ABE的距离．
1 1 1
 1 2 2   1
又平面ABE的单位法向量n  , , ，FB 0,0, ，
1 0 3 3 3 1  2
  1
所以直线FC 到平面ABE的距离为 FB n  ，故D正确．
1 1 1 0 3
故选：ABD
12．0.52
【详解】由题意可得反面朝上次数为1004852，
52
所以设反面朝上为事件A，则事件A出现的频率为PA 0.52.
100
故答案为：0.52.
13【答案】
2 2
【详解】因为四边形ABFE、CDEF都是边长为
2
的正方形，则AEEF，DE EF，
 
又平面ABFE与平面CDEF夹角为60，即AED60o，则 EA,ED 60，
          
因为 DBDEEAABEAEDAB ，由图易知 ABEA ， ABED ，
   
所以 DB   EAEDAB 2
        
2 2 2
 EA ED  AB 2EAED2EAAB2EDAB
，
 444222cos6000 2 2
即B，D两点间的距离是2 2.
故答案为：2 2.
14.【答案】 2
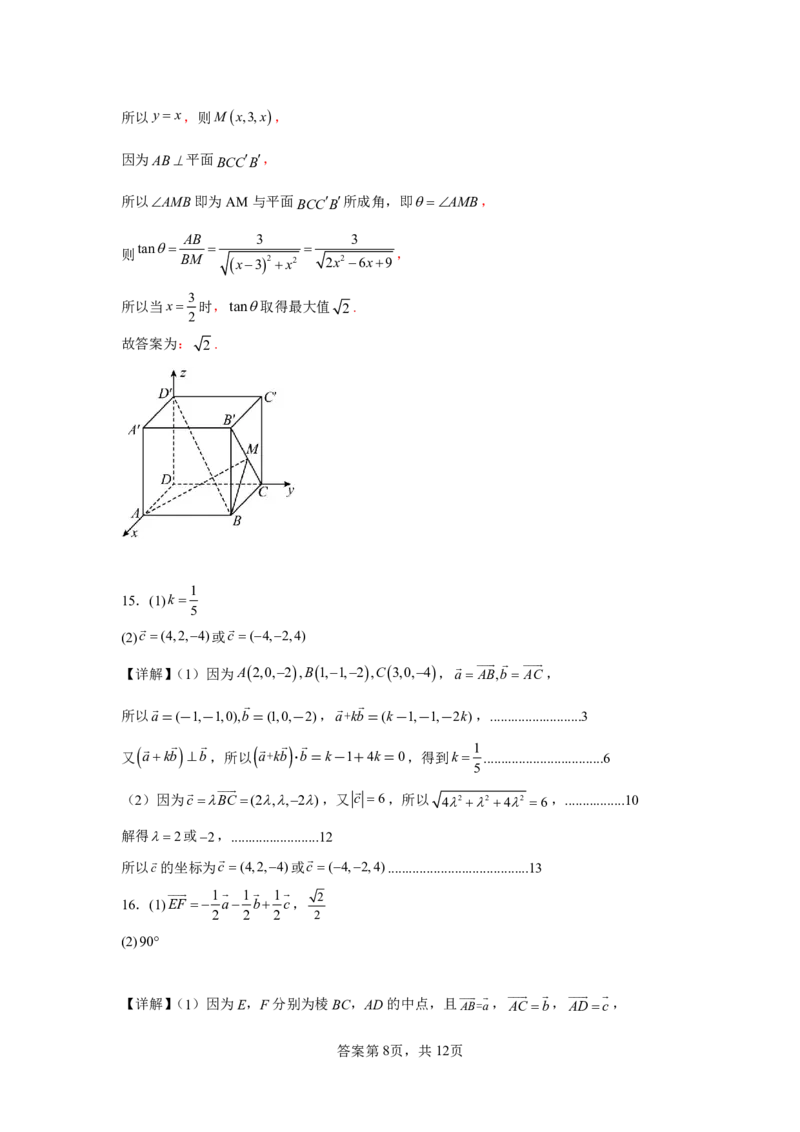
【解析】如图，以D为原点建立空间直角坐标系，
则A3,0,0,B3,3,0,D0,0,3，
设Mx,3,y x,y 0,3  ，
 
则AM x3,3,y,BD 3,3,3，
因为AM BD，
 
所以AM BDx3,3,y3,3,33x393y  0 ，
答案第7页，共12页
{#{QQABTQKAggiIAJAAAQgCAwFoCEGQkBGAAYgORBAEsAAASBNABCA=}#}所以y x，则Mx,3,x，
因为AB平面
BCC

B
，
所以AMB即为AM与平面
BCC

B
所成角，即AMB，
AB 3 3
tan  
则 ，
BM x32x2 2x26x9
3
所以当x 时，tan取得最大值 2.
2
故答案为： 2.
1
15．(1)k 
5
 
(2)c (4,2,4)或c (4,2,4)
【详解】（1）因为A2,0,2,B1,1,2,C3,0,4，a    A  B  ,b    A  C  ，
   
所以a=(-1,-1,0),b=(1,0,-2)，a+kb=(k-1,-1,-2k)，..........................3
又  a  kb   b  ，所以(a  +kb  )×b  =k-1+4k=0，得到k  1 ..................................6
5
  
（2）因为c BC(2,,2)，又 c 6，所以 42242 6 ，.................10
解得2或2，.........................12
所以c 的坐标为c  (4,2,4)或c  (4,2,4)........................................13
 1 1 1
2
16．(1)EF  a b c，
2 2 2 2
(2)90
     
【详解】（1）因为E，F分别为棱BC，AD的中点，且 AB=a ，ACb，ADc，
答案第8页，共12页
{#{QQABTQKAggiIAJAAAQgCAwFoCEGQkBGAAYgORBAEsAAASBNABCA=}#}    1  1 1     1
可得EF EBBAAF  CBAB AD ABAC AB AD
2 2 2 2
1uuur 1uuur 1uuur 1r 1r 1r
 AB AC AD a b c，..............................4
2 2 2 2 2 2
         1
因为正四面体ABCD的棱长为1，则 a  b  c 1，且abacbc ，
2
 2  1  1  1  2 1  1  1  1   1   1  
可得 EF  a b  c  a 2 b 2 c 2 ab  ac bc
 2 2 2  4 4 4 2 2 2
1 1 1 1 1 1 1 1 1 1
          ，.......................................9
4 4 4 2 2 2 2 2 2 2
 2 2
即 EF  ，所以EF的长为 .................................................10
2 2
    1  1 1  1   
（2）由题意得GH GAADDH  ABAD DC  ABAD ACAD
2 2 2 2
1uuur 1uuur 1uuur 1r 1r 1r
 AB AC AD  a b c，................................12
2 2 2 2 2 2
  1    1   1    
因此EFGH  abc   abc  a2b2c22ac
2  2 4
1 1
 1112 0，.............................14
4 2
   
即EF GH ，即 EF 与GH的夹角为90....................15
5
17．(1)
16
7
(2)
8
【详解】（1）设甲袋中的红球为r,r ，白球为w，篮球为b，
1 2
乙袋中的红球为R，白球W，篮球为B,B ，
1 2
则从两袋中各取一球，所有基本事件如下：
r,R,r,W,r,B,r,B ，w,R,w,W,w,B,w,B ，
1 1 1 1 1 2 1 1 2
r ,R,r ,W,r ,B,r ,B ，b,R,b,W,b,B,b,B ，
2 2 2 1 2 2 1 2
故基本事件的总数为16.........................................3
设A为“取到的两球颜色相同”，则A含有的基本事件如下：
r,R,r ,R,w,W,b,B,b,B ,..........................................5
1 2 1 2
5 5
共5个基本事件，则PA  ............................................................7
44 16
（2）如（1）中所设，从甲袋中随机取两球，从乙袋中随机取一球，总的基本事件如下：
答案第9页，共12页
{#{QQABTQKAggiIAJAAAQgCAwFoCEGQkBGAAYgORBAEsAAASBNABCA=}#}r,r ,R,r,r ,W,r,r ,B,r,r ,B ，r,w,R,r,w,W,r,w,B,r,w,B ，
1 2 1 2 1 2 1 1 2 2 1 1 1 1 1 2
r,b,R,r,b,W,r,b,B,r,b,B ，r ,b,R,r ,b,W,r ,b,B,r ,b,B ，
1 1 1 1 1 2 2 2 2 1 2 2
r ,w,R,r ,w,W,r ,w,B,r ,w,B ，b,w,R,b,w,W,b,w,B,b,w,B ，
2 2 2 1 2 2 1 2
基本事件的总数为24，............................10
设B为“取到至少一个红球”，其对立事件设为C，则C为“没有取到红球”，
C含有的基本事件如下：b,w,W,b,w,B,b,w,B ，共有3个，...............13
1 2
3 1 1 7
故PC  ，故PB1PC1  ..........................15
24 8 8 8
18．(1)证明见解析
10
(2)
5
1
(3)
5
【详解】（1）因为PCPD，O为CD的中点，
所以POCD．.......................................1
又因为平面PCD平面ABCD，平面PCD平面ABCDCD，PO平面PCD，
所以PO平面ABCD．....................2
因为CD2，PCPD，PCPD，所以PO1．
取AB的中点E，连接OE，则OE⊥CD，
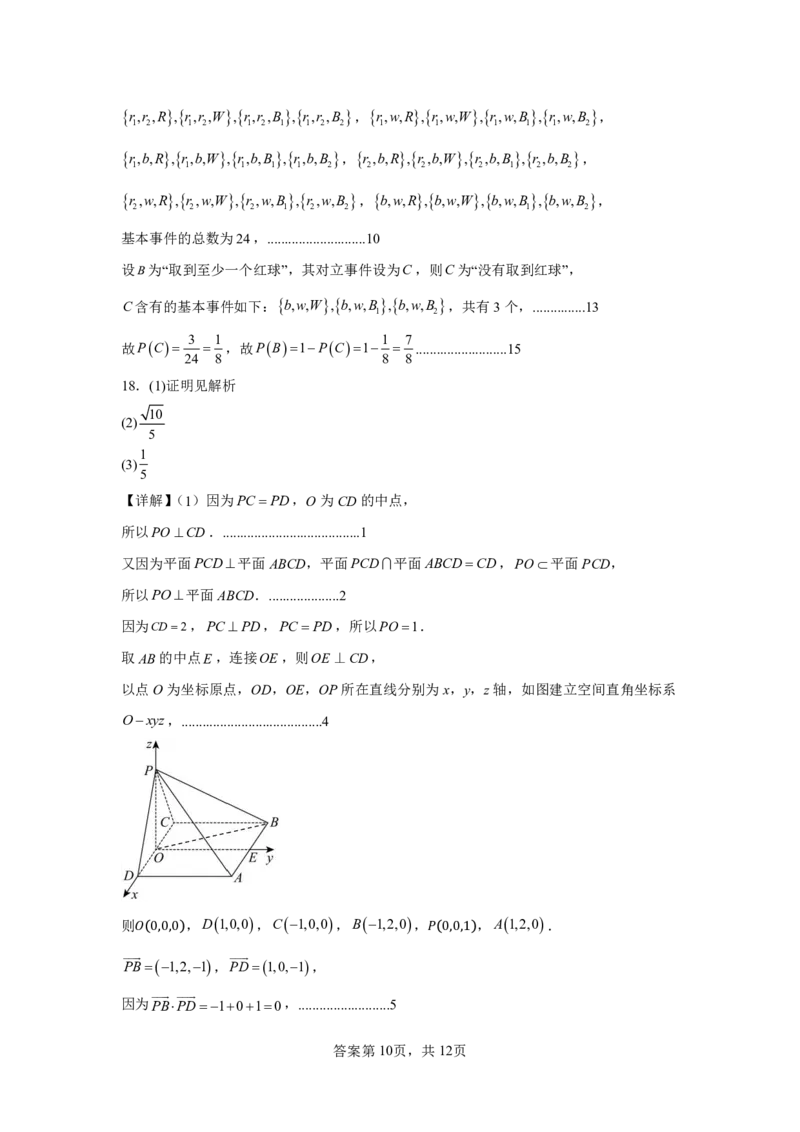
以点O为坐标原点，OD，OE，OP所在直线分别为x，y，z轴，如图建立空间直角坐标系
Oxyz，........................................4
则 ，D1,0,0，C1,0,0，B1,2,0， ，A1,2,0．
   0,0,0   0,0,1
PB1,2,1，PD1,0,1，
 
因为PBPD1010，..........................5
答案第10页，共12页
{#{QQABTQKAggiIAJAAAQgCAwFoCEGQkBGAAYgORBAEsAAASBNABCA=}#}所以PBPD．
（2）设平面PAB的一个法向量为 ，
 m    A  P  0 x2yz0  =  ,  , 
则 m    A  B  0 ，即  2x0 ，..................................7

解得x0，令y1，则z2，则m0,1,2．..............................9
设直线PC与平面PAB所成的角为，

又PC 1,0,1，
 
  mPC 0,1,21,0,1 2 10
则sin cos m,PC       ，
m PC 14 11 5 2 5
10
所以直线PC与平面PAB所成的角的正弦值为 ．..............10
5

（3）设平面POB的一个法向量为na,b,c，
 
 nOP0  c0
则 n  O  B  0 ，即 a2b0 ,...................................12

解得c0，令b1，则 ，故n2,1,0．..................14
设平面POB与平面PAB  的 = 夹 2 角为，
  m  n  0,1,22,1,0 1 1
则cos cos m,n       ．
m n 14 41 5 5 5
1
故平面POB与平面PAB的夹角的余弦值为 ．........................17
5
1
19．(1)
4
2
(2)
3
5
(3) .
16
【详解】（1）依题意，设事件M “甲两轮都答对问题”，N “乙两轮都答对问题”，
3 3 9 2 2 4
所以PM   ,PN  
4 4 16 3 3 9
因为事件M,N相互独立，
9 4 1
所以两人在两轮比赛中都答对的概率为PMNPMPN   .........5
16 9 4
（2）设事A“甲第一轮答对”，B“乙第一轮答对”，
答案第11页，共12页
{#{QQABTQKAggiIAJAAAQgCAwFoCEGQkBGAAYgORBAEsAAASBNABCA=}#}C“甲第二轮答对”，D=“乙第二轮答对”，
E “两人在两轮比赛中至少答对3道题”，
则E  ABCDABCDABCDABCDABCD，
由事件的独立性与互斥性，
可得P(E)P(ABCD)P(ABCD)P(ABCD)P(ABCD)P(ABCD)
P(A)P(B)P(C)P(D)P(A)P(B)P(C)P(D)P(A)P(B)P(C)P(D)P(A)P(B)P
(C)P(D)P(A)P(B)P(C)P(D).
3 2 3 2 1 2 3 2 3 1 3 2 3 2 1 2 3 2 3 1 2
                    
4 3 4 3 4 3 4 3 4 3 4 3 4 3 4 3 4 3 4 3 3
2
故两人在两轮比赛中至少答对3道题的概率为 ....................................10
3
（3）设事件A ,A 分别表示甲三轮答对2个，3个题目，
2 3
B ,B 分别表示乙三轮答对2个，3个题目，
2 3
3
3 3 1 27 3  27
则PA 3    ,P A     ，
2 4 4 4 64 3 4  64
3
2 2 1 4 2 8
PB 3    ,PB    ，.............................15
2 3 3 3 9 3 3 27
设事件Q“两人在三轮比赛中，甲和乙各自答对题目的个数相等且至少为2”，
则Q AB AB ，且A ,A,B ,B 分别相互独立，
2 2 3 3 2 3 2 3
27 4 27 8
所以PQPA B PAB PA PB PA PB    
2 2 3 3 2 2 3 3 64 9 64 27
5
 ............................17
16
5
所以两人在三轮比赛中，甲和乙各自答对题目的个数相等且至少为2的概率为 .
16
答案第12页，共12页
{#{QQABTQKAggiIAJAAAQgCAwFoCEGQkBGAAYgORBAEsAAASBNABCA=}#}