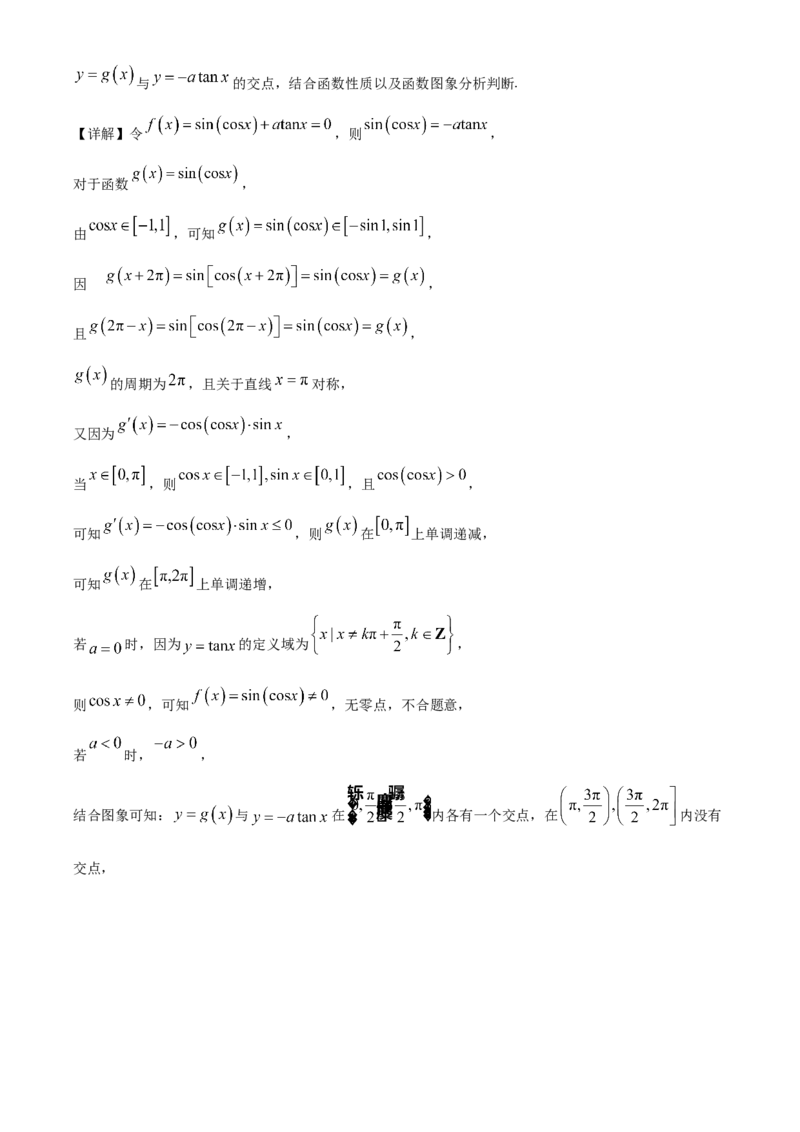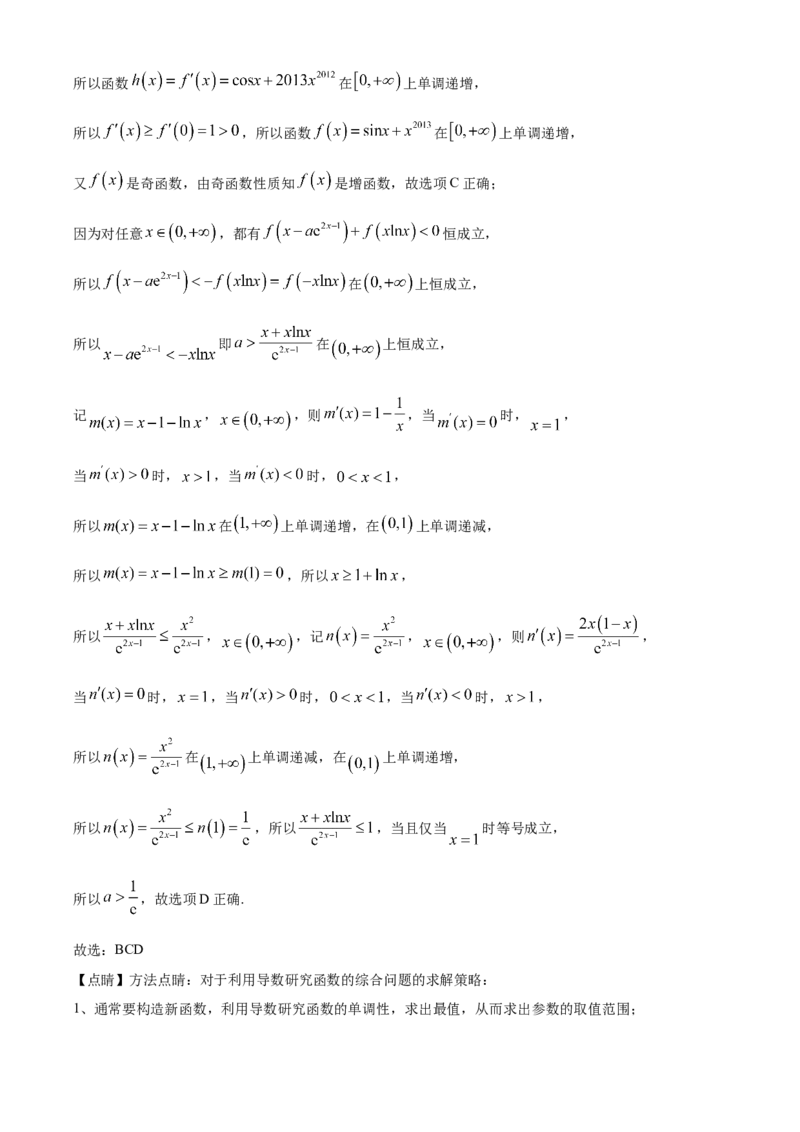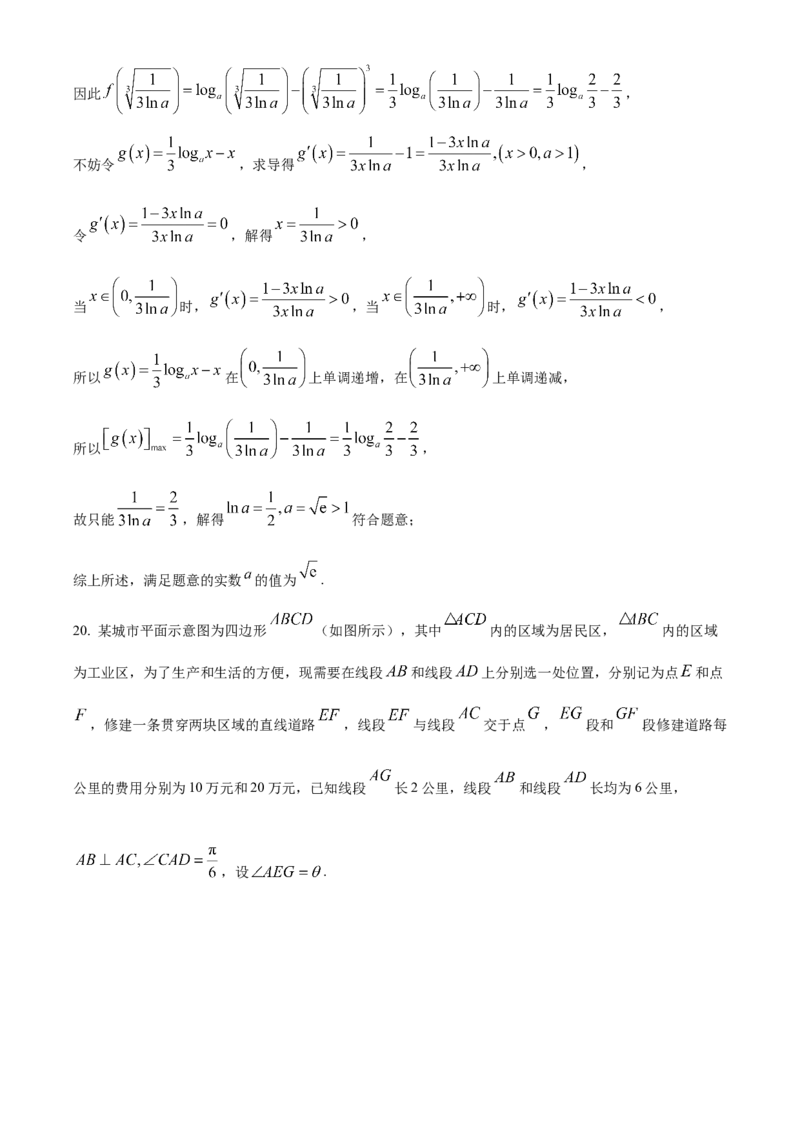文档内容
华中师大一附中 2023-2024 学年度上学期高三期中检测
数学试题
命题人:余文抒 徐聪 王文莹 审题人:王文莹
试卷满分:150分 考试时间:120分钟
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有
一项是符合题目要求的.
1. 已知复数 满足 ,则 的模为( )
A. 1 B. 2 C. 5 D.
【答案】D
【解析】
【分析】先化简求出 ,再根据共轭复数定义求出 ,最后根据模长公式求解即可.
【详解】 ,
,
.
故选:D.
2. 已知集合 ,则 ( )
A. B. C. D.
【答案】C
【解析】
【分析】利用指数函数单调性求解集合A,从而求解 ,利用对数函数单调性结合整数概念求解集合
B,最后利用交集运算即可求解.
【详解】因为集合 ,所以 ,
又 ,所以 .
故选:C
3. 在 中,“ ”是“ ”的( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
【答案】B
【解析】
【分析】结合正弦函数的性质由 ,可得 ,再根据充分条件和必要条件的定义判断即可.
【详解】在 中, ,
由 ,可得 ,
所以“ ”是“ ”的必要不充分条件.
故选:B.
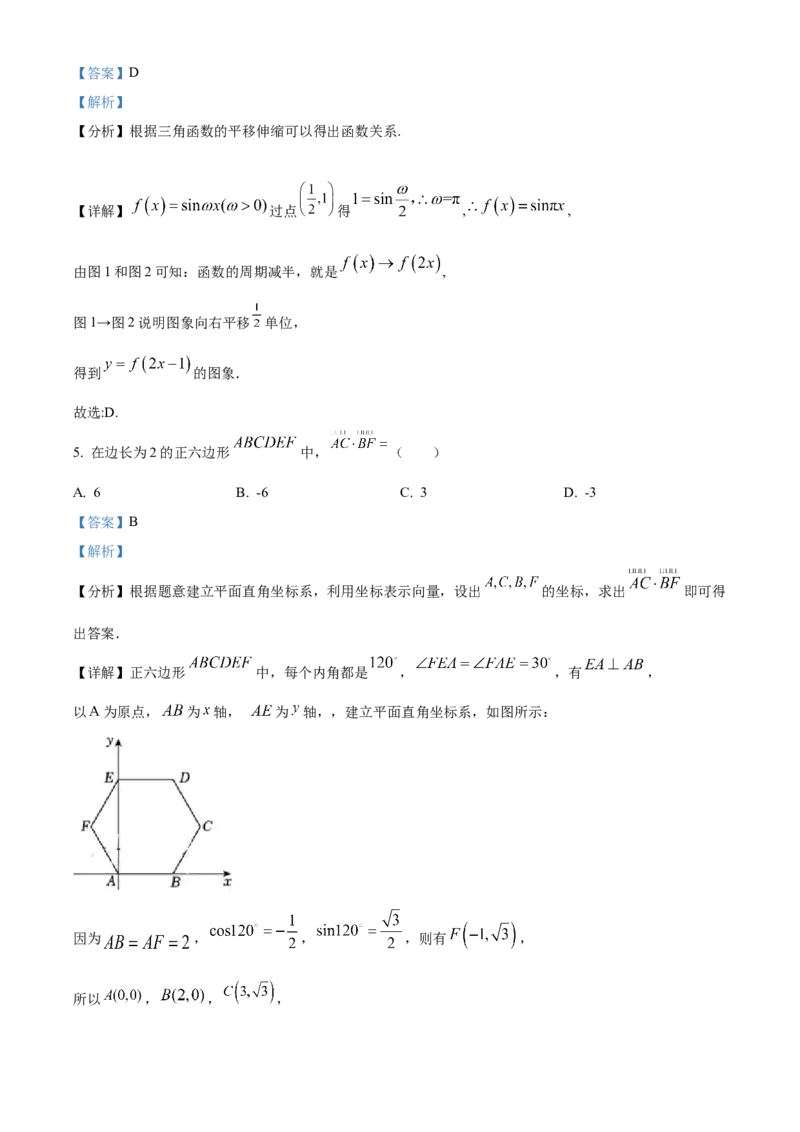
4. 已知函数 的图象的一部分如图1,则图2中的函数图像对应的函数是( )
A. B.
C. D.【答案】D
【解析】
【分析】根据三角函数的平移伸缩可以得出函数关系.
【详解】 过点 得 , ,
由图1和图2可知:函数的周期减半,就是 ,
图1→图2说明图象向右平移 单位,
得到 的图象.
故选:D.
5. 在边长为2的正六边形 中, ( )
A. 6 B. -6 C. 3 D. -3
【答案】B
【解析】
【分析】根据题意建立平面直角坐标系,利用坐标表示向量,设出 的坐标,求出 即可得
出答案.
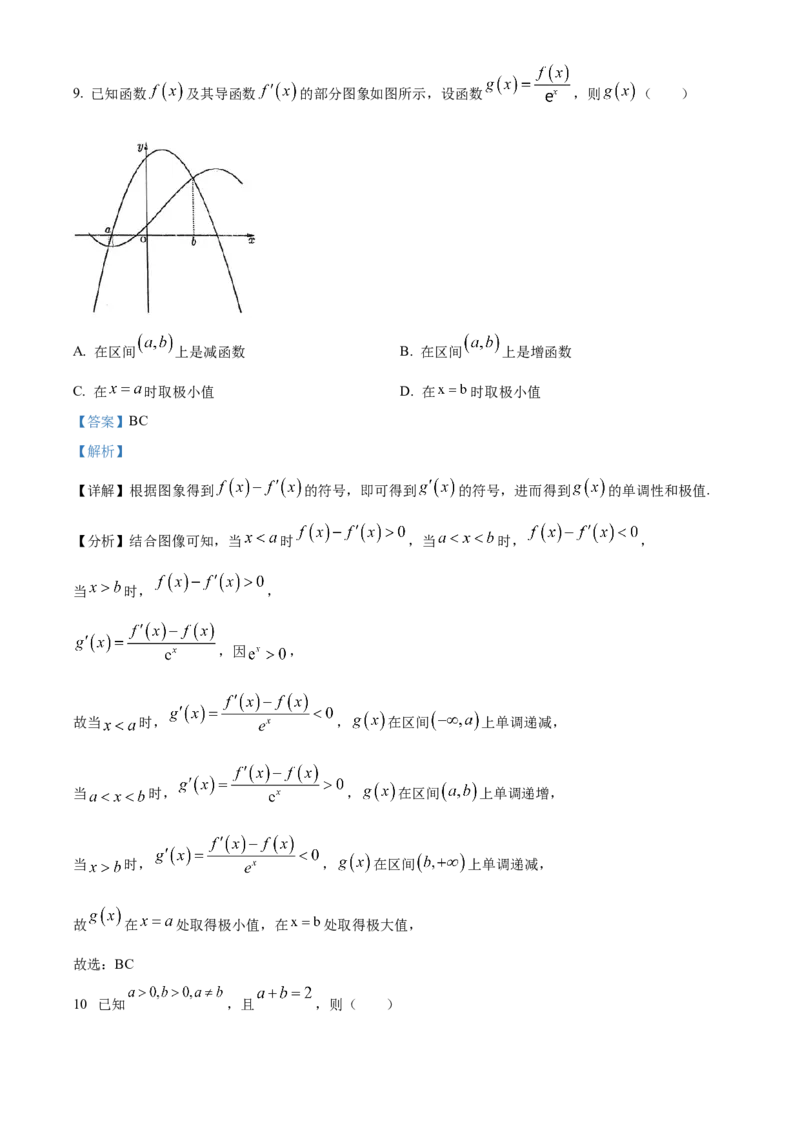
【详解】正六边形 中,每个内角都是 , ,有 ,
以 为原点, 为 轴, 为 轴,,建立平面直角坐标系,如图所示:
因为 , , ,则有 ,
所以 , , ,, ,
由平面向量数量积的运算可得 .
故选:B.
6. 在声学中,音量被定义为: ,其中 是音量(单位为dB), 是基准声压为
,P是实际声音压强.人耳能听到的最小音量称为听觉下限阈值.经过研究表明,人耳对于不同频
率的声音有不同的听觉下限阈值,如下图所示,其中240 对应的听觉下限阈值为20 ,1000 对应
的听觉下限阈值为0 ,则下列结论正确的是( )
A. 音量同为20 的声音,30~100 的低频比1000~10000 的高频更容易被人们听到.
B. 听觉下限阈值随声音频率的增大而减小.
C. 240 的听觉下限阈值的实际声压为0.002 .
D. 240 的听觉下限阈值的实际声压为1000 的听觉下限阈值实际声压的10倍.
【答案】D
【解析】
【分析】对于选项A、B,可以直接观察图像得出听觉下限阈值与声音频率的关系进行判断;对于C、D,
通过所给函数关系 代入听觉下限阈值计算即可判断.
【详解】对于A, 30~100 的低频对应图像的听觉下限阈值高于20 ,1000~10000 的高频对应的听觉下限阈值低于20 ,所以对比高频更容易被听到,故A错误;
对于B,从图像上看,听觉下限阈值随声音频率的增大有减小也有增大,故B错误;
对于C,240 对应的听觉下限阈值为20 , ,
令 ,此时 ,故C错误;
对于D,1000 的听觉下限阈值为0 ,
令 ,此时 ,所以240 的听觉下限阈值的实际声压为1000 的听觉下限阈值
实际声压的10倍,故D正确.
故选:D.
7. 若实数 满足 ,则 的大小关系为( )
A. B.
C. D.
【答案】A
【解析】
【分析】由切线放缩可求 ,根据对数函数性质和正弦值域可判断 ,由不等式的关系可判断 .
【详解】因为 ,当 时,设 ,则 ,易知当 时,
,当 时, 单调递增,所以 ;
所以 ;
由已知可得 ,因为 ,所以 ; ,所以 ;
因为 ,所以 ;
故 ;
故选:A8. 已知函数 在区间 上恰有两个极值点,且 ,
则 的值可以是( )
A. 6 B. 7 C. 8 D. 9
【答案】C
【解析】
【分析】先根据辅助角公式计算化简函数,再结合选项得出矛盾判断A,B,D选项,再计算说明C选项正确
即可.
【详解】 ,
当 时, ,A
选项错误;
当 时, ,B 选
项错误;
当 时, ,
, 恰有三个极值点,D选项错误;
当 时 , ,
, 恰有两个极值点,C选项正确;
故选:C.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9. 已知函数 及其导函数 的部分图象如图所示,设函数 ,则 ( )
A. 在区间 上是减函数 B. 在区间 上是增函数
C. 在 时取极小值 D. 在 时取极小值
【答案】BC
【解析】
【详解】根据图象得到 的符号,即可得到 的符号,进而得到 的单调性和极值.
【分析】结合图像可知,当 时 ,当 时, ,
当 时, ,
,因 ,
故当 时, , 在区间 上单调递减,
当 时, , 在区间 上单调递增,
当 时, , 在区间 上单调递减,
故 在 处取得极小值,在 处取得极大值,
故选:BC
.
10 已知 ,且 ,则( )A. B.
C. D.
【答案】ABC
【解析】
【分析】根据基本不等式即可结合选项逐一求解.
【详解】 ,当且仅当 ,即 时
取等号,由于 ,所以 ,A正确,
由于 , ,当且仅当 且 时,即 时取等号,
由于 ,所以 ,B正确,
由 以及 可得 ,
当且仅当 ,即 时取等号,由于 ,所以 ,故C正确,
,当且仅当 ,即 时取等号,由于 ,
所以D错误,
故选:ABC
11. 若函数 在区间 有2024个零点,则整数 可以是( )
A. 2022 B. 2023 C. 2024 D. 2025
【答案】BCD
【解析】
【分析】令 ,则 ,将函数零点转化为两个函数与 的交点,结合函数性质以及函数图象分析判断.
【详解】令 ,则 ,
对于函数 ,
由 ,可知 ,
因 为 ,
且 ,
的周期为 ,且关于直线 对称,
又因为 ,
当 ,则 ,且 ,
可知 ,则 在 上单调递减,
可知 在 上单调递增,
若 时,因为 的定义域为 ,
则 ,可知 ,无零点,不合题意,
若 时, ,
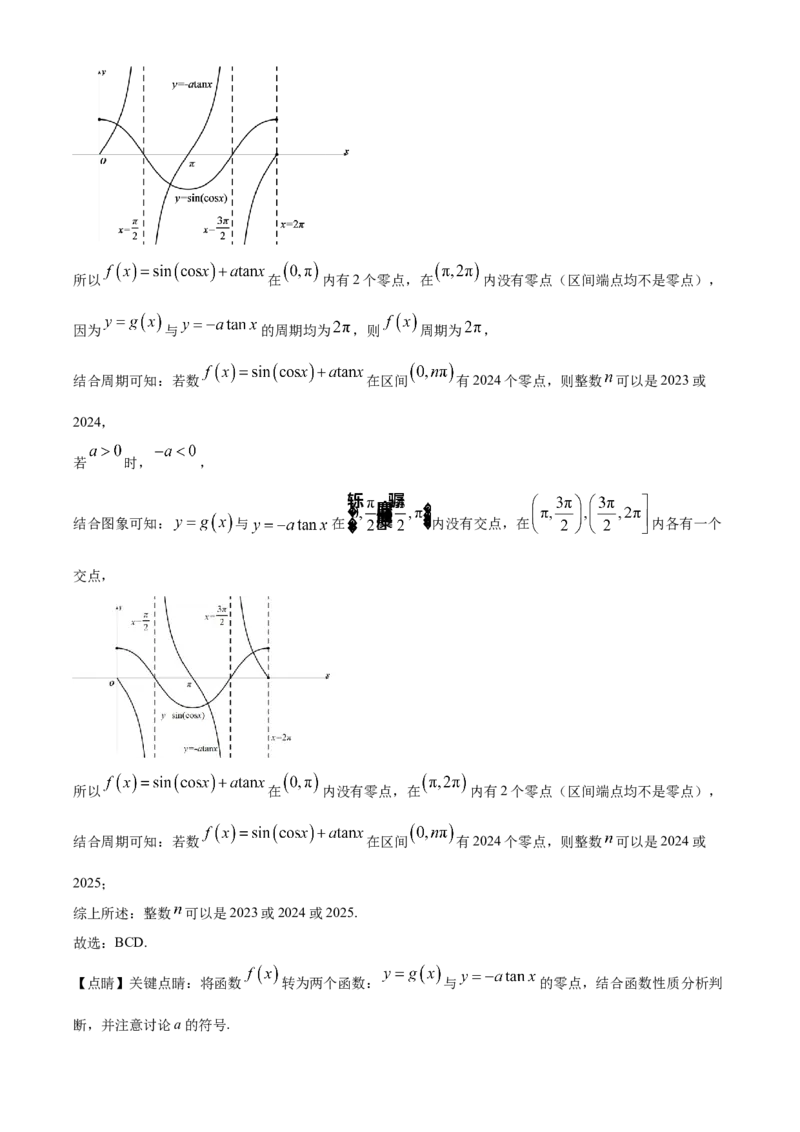
结合图象可知: 与 在 内各有一个交点,在 内没有
交点,所以 在 内有2个零点,在 内没有零点(区间端点均不是零点),
因为 与 的周期均为 ,则 周期为 ,
结合周期可知:若数 在区间 有2024个零点,则整数 可以是2023或
2024,
若 时, ,
结合图象可知: 与 在 内没有交点,在 内各有一个
交点,
所以 在 内没有零点,在 内有2个零点(区间端点均不是零点),
结合周期可知:若数 在区间 有2024个零点,则整数 可以是2024或
2025;
综上所述:整数 可以是2023或2024或2025.
故选:BCD.
【点睛】关键点睛:将函数 转为两个函数: 与 的零点,结合函数性质分析判
断,并注意讨论a的符号.12. 已知定义在 上的函数 图象上任意一点 均满足 ,且对任
意 ,都有 恒成立,则下列说法正确的是( )
A. B. 是奇函数
C. 是增函数 D.
【答案】BCD
【解析】
【分析】利用函数 的单调性可求 判断A,根据奇函数的定义判断B,根
据导数符号判断函数的单调性判断C,根据奇函数和单调性把不等式化为 在 上恒成
立,构造函数求解最值即可判断D.
【详解】 ,有 ,
记 ,则 ,所以 在 上单调递增,
所以 ,所以 ,故选项A错误;
因为 且定义域 关于原点对称,
所以 是奇函数,故选项B正确;
记 , ,则 , ,
对 ,因为 ,则 ,
即函数 在 单调递减,
又 时, ,则 ,即 ,根据幂函数性质知 ,
所以 ,所以函数 在 上单调递增,
所以 ,所以函数 在 上单调递增,
又 是奇函数,由奇函数性质知 是增函数,故选项C正确;
因为对任意 ,都有 恒成立,
所以 在 上恒成立,
所以 即 在 上恒成立,
记 , ,则 ,当 时, ,
当 时, ,当 时, ,
所以 在 上单调递增,在 上单调递减,
所以 ,所以 ,
所以 , ,记 , ,则 ,
当 时, ,当 时, ,当 时, ,
所以 在 上单调递减,在 上单调递增,
所以 ,所以 ,当且仅当 时等号成立,
所以 ,故选项D正确.
故选:BCD
【点睛】方法点睛:对于利用导数研究函数的综合问题的求解策略:
1、通常要构造新函数,利用导数研究函数的单调性,求出最值,从而求出参数的取值范围;2、利用可分离变量,构造新函数,直接把问题转化为函数的最值问题.
的
3、根据恒成立或有解求解参数 取值时,一般涉及分离参数法,但压轴试题中很少碰到分离参数后构造
的新函数能直接求出最值点的情况,进行求解,若参变分离不易求解问题,就要考虑利用分类讨论法和放
缩法,注意恒成立与存在性问题的区别.
三、填空题:本题共4小题,每小题5分,满分20分
13. 若直线 与曲线 相切,则 __________.
【答案】1
【解析】
【分析】求导,结合导数的几何意义分析求解.
【详解】因为 ,则 ,
设切点坐标为 ,则 ,解得 .
故答案为:1.
14. 杭州第 届亚洲运动会,于 年 月 日至 月 日在中国浙江省杭州市举行,本届亚运会的会
徽名为“潮涌”,主体图形由扇面、钱塘江、钱江潮头、赛道、互联网符号及象征亚奥理事会的太阳图形
六个元素组成(如图),其中扇面造型突出反映了江南的人文意蕴.已知该扇面呈扇环的形状,内环和外环
均为圆周的一部分,若内环弧长是所在圆周长的 ,内环所在圆的半径为 ,径长(内环和外环所在圆的
半径之差)为 ,则该扇面的面积为__________.
【答案】
【解析】【分析】根据题意求出内环圆弧所对的圆心角,并求出外环圆弧所在圆的半径,利用扇形的面积公式可求
得该扇面的面积.
【详解】设内环圆弧所对的圆心角为 ,因为内环弧长是所在圆周长的 ,且内环所在圆的半径为 ,
所以, ,可得 ,
因为径长(内环和外环所在圆的半径之差)为 ,所以,外环圆弧所在圆的半径为 ,
因此,该扇面的面积为 .
故答案为: .
15. 一只钟表的时针 与分针 长度分别为3和4,设0点为0时刻,则 的面积 关于时间 (单
位:时)的函数解析式为__________,一昼夜内(即 时), 取得最大值的次数为__________.
【答案】 ①. ( ,且 ) ②. 44
【解析】
的
【分析】根据给定条件,求出 ,再利用三角形面积公式列式即得;探求面积函数 周期即可计算
得解.
【详解】 旋转的角速度为 , 旋转的角速度为 ,
或 , ,
,而当 时,不能构成三角形,
所以 ( ,且 );显然函数 的周期为 且每个周期仅出现一次最大值,而 ,
所以 取得最大值的次数为 .
故答案为: ( ,且 );44
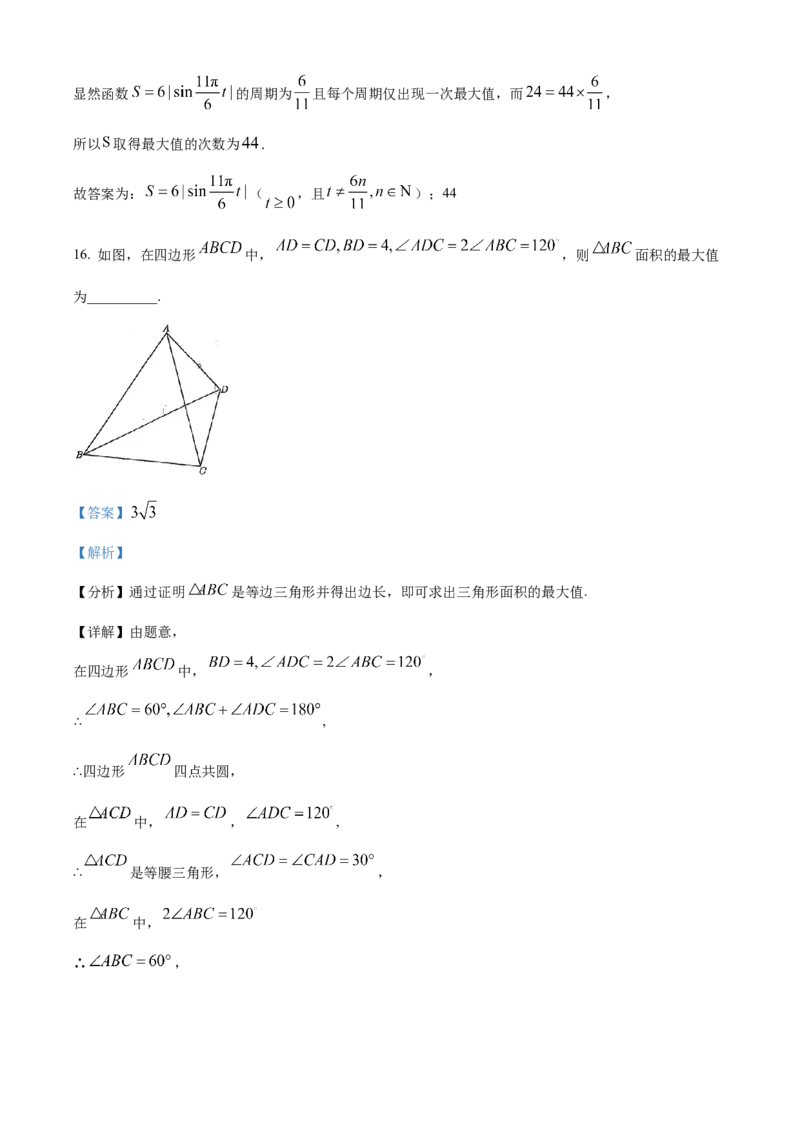
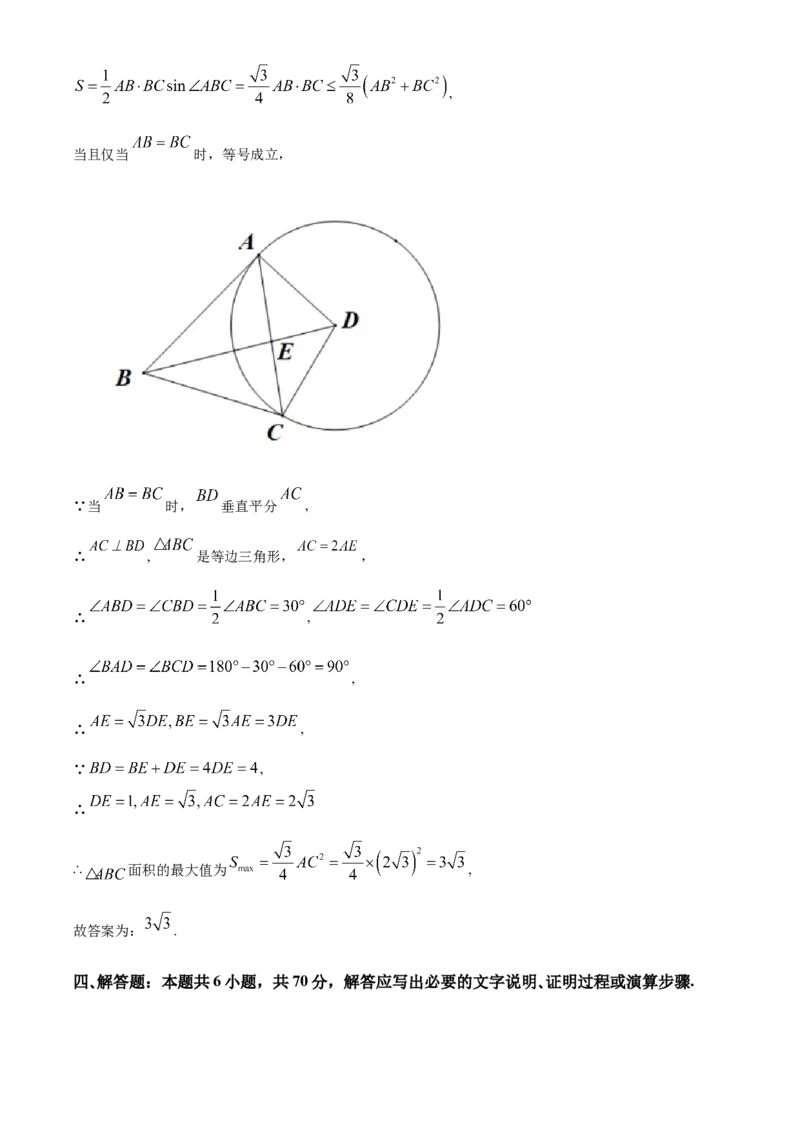
16. 如图,在四边形 中, ,则 面积的最大值
为__________.
【答案】
【解析】
【分析】通过证明 是等边三角形并得出边长,即可求出三角形面积的最大值.
【详解】由题意,
在四边形 中, ,
∴ ,
∴四边形 四点共圆,
在 中, , ,
∴ 是等腰三角形, ,
在 中,
∴ ,,
当且仅当 时,等号成立,
∵当 时, 垂直平分 ,
∴ , 是等边三角形, ,
∴ ,
∴ ,
∴ ,
∵ ,
∴
∴ 面积的最大值为 ,
故答案为: .
四、解答题:本题共6小题,共70分,解答应写出必要的文字说明、证明过程或演算步骤.17. 已知
(1)求 的单调递增区间与对称中心;
(2)当 时, 的取值范围为 ,求实数 的取值范围.
【答案】(1) ,
(2)
【解析】
【分析】(1)先利用三角恒等变换将函数表达式化简,然后根据正弦的单调递增区间与对称中心的定义
计算即可得解.
(2)画出函数图象分析可知当且仅当 时,其中 ,
,满足题意,从而计算即可得解.
【小问1详解】
由题意
,
令 ,解得 ,
令 ,解得 ,
所以 的单调递增区间与对称中心分别为 , .
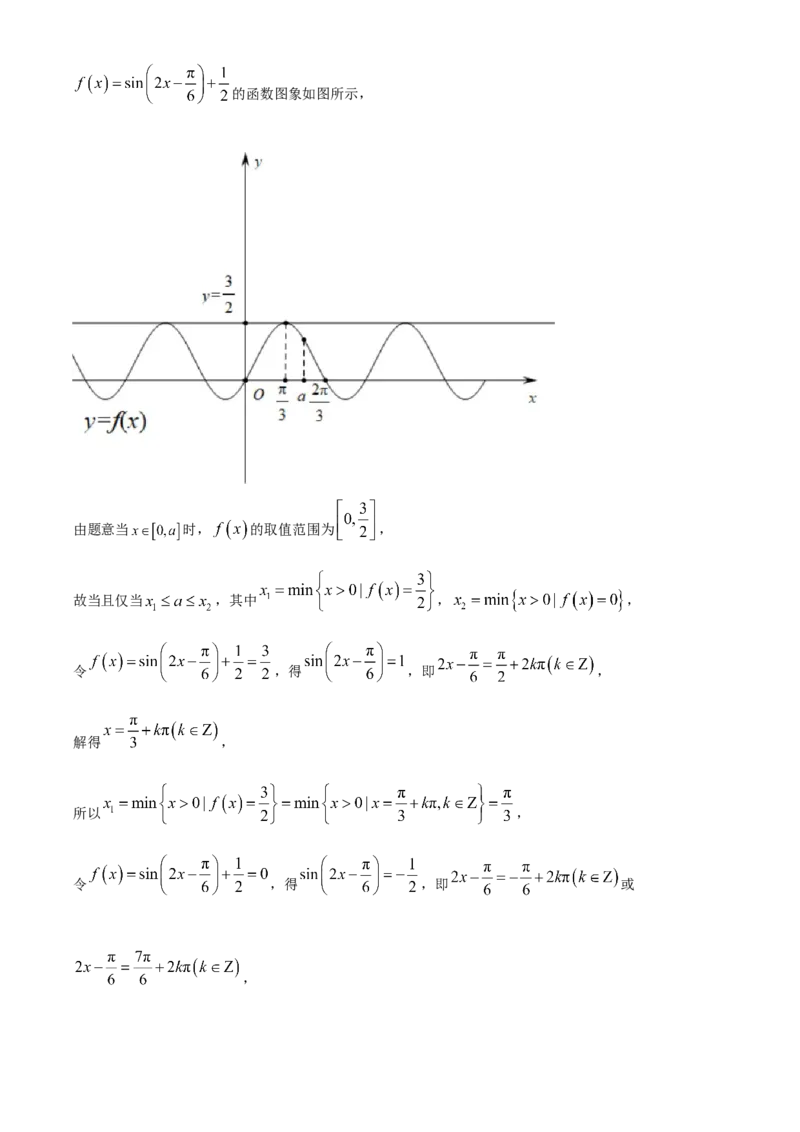
【小问2详解】的函数图象如图所示,
由题意当 时, 的取值范围为 ,
故当且仅当 ,其中 , ,
令 ,得 ,即 ,
解得 ,
所以 ,
令 ,得 ,即 或
,解得 或 ,
所以 ,
综上所述:满足题意的实数 的取值范围为 .
18. 记 的内角 的对边分别为 ,已知 .
(1)求A的值;
(2)若 的平分线与 交于点 ,求 面积的最小值.
【答案】(1)
(2)
【解析】
【分析】(1)根据题意,利用正弦定理和三角恒等变换化简得 ,再结合正弦函数的性质
分析求解;
(2)根据题意得 ,结合 ,得到 ,结合基本不等式
即可求解.
【小问1详解】
因为 ,由正弦定理可得 ,
则 ,
,
即 ,可得 ,
因为 ,则 ,则 ,
整理得 ,
又因为 ,则 ,
可得 ,所以 .
【小问2详解】
因为 平分 且 ,所以 ,
由 ,可得 ,
整理得 ,则 ,当且仅当 时,等号成立,
故 面积的最小值为 .
19. 已知函数 且 ,
(1)求函数 的单调区间;
(2)若函数 有最大值 ,求实数 的值.
【答案】(1)答案见解析
(2)
【解析】
【分析】(1)首先对 求导,然后分 和 讨论导函数的符号,从而即可得解.(2)结合(1)中分析可知,当且仅当 ,通过构造函数
,说明 即可得解.
【小问1详解】
由题意 ,分以下两种情形来讨论函数 的单调区间,
情形一:当 时, ,
所以 的单调递减区间为 ,没有单调递增区间.
情形二:当 时,令 ,
解得 ,
当 时, ,当 时, ,
所以 的单调递增区间为 ,单调递减区间为 .
综上所述:当 时, 的单调递减区间为 ,没有单调递增区间;
当 时, 的单调递增区间为 ,单调递减区间为 .
【小问2详解】
由题意若函数 有最大值 ,
则由(1)可知当且仅当 时, 有最大值 ,因此 ,
不妨令 ,求导得 ,
令 ,解得 ,
当 时, ,当 时, ,
所以 在 上单调递增,在 上单调递减,
所以 ,
故只能 ,解得 符合题意;
综上所述,满足题意的实数 的值为 .
20. 某城市平面示意图为四边形 (如图所示),其中 内的区域为居民区, 内的区域
为工业区,为了生产和生活的方便,现需要在线段 和线段 上分别选一处位置,分别记为点 和点
,修建一条贯穿两块区域的直线道路 ,线段 与线段 交于点 , 段和 段修建道路每
公里的费用分别为10万元和20万元,已知线段 长2公里,线段 和线段 长均为6公里,
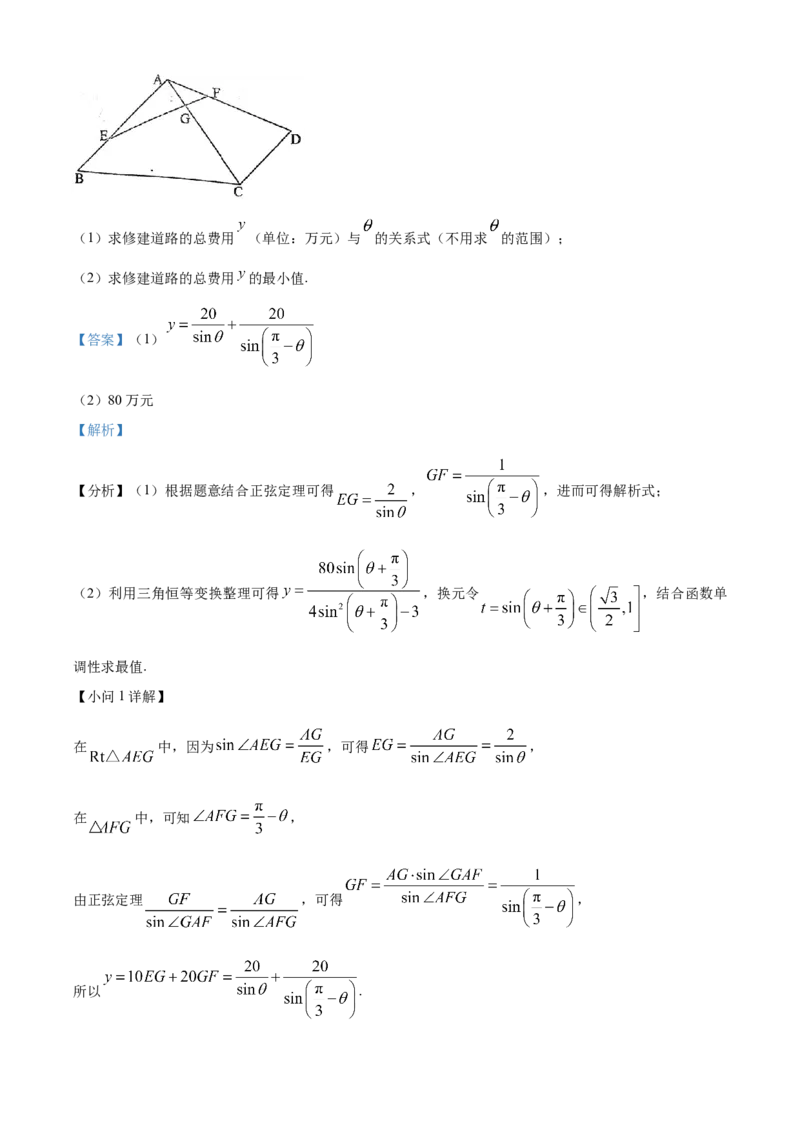
,设 .(1)求修建道路的总费用 (单位:万元)与 的关系式(不用求 的范围);
(2)求修建道路的总费用 的最小值.
【答案】(1)
(2)80万元
【解析】
【分析】(1)根据题意结合正弦定理可得 , ,进而可得解析式;
(2)利用三角恒等变换整理可得 ,换元令 ,结合函数单
调性求最值.
【小问1详解】
在 中,因为 ,可得 ,
在 中,可知 ,
由正弦定理 ,可得 ,
所以 .【小问2详解】
由(1)可知:
,
因为 ,则 ,
令 ,则 ,
且 在 上单调递增,可知 在 上单调递增,
所以 在 上单调递减,
当 ,即 时,修建道路的总费用 取到最小值 万元.
21. 已知函数
(1)求 的零点个数;
(2)若 恒成立,求整数 的最大值.
【答案】(1)2个 (2)
【解析】
【分析】(1)令 可得 ,利用导数判断出函数 在上的单调性,利用函数与方程的思想画出函数 与 在 内的图象,
根据交点个数即可求得 的零点个数;
(2)易知 , 在 上恒成立,则可得
,求出 在 上的最小值即可得
,便可知整数 的最大值为 .
【小问1详解】
根据由题意可知,令 ,
又 ,整理可得 ;
令 ,则 ,
显然当 时, 恒成立,
所以可得 在 上单调递减,且 在 上恒成立,
易知函数 在 上单调递减,在 上单调递增;
且 ,
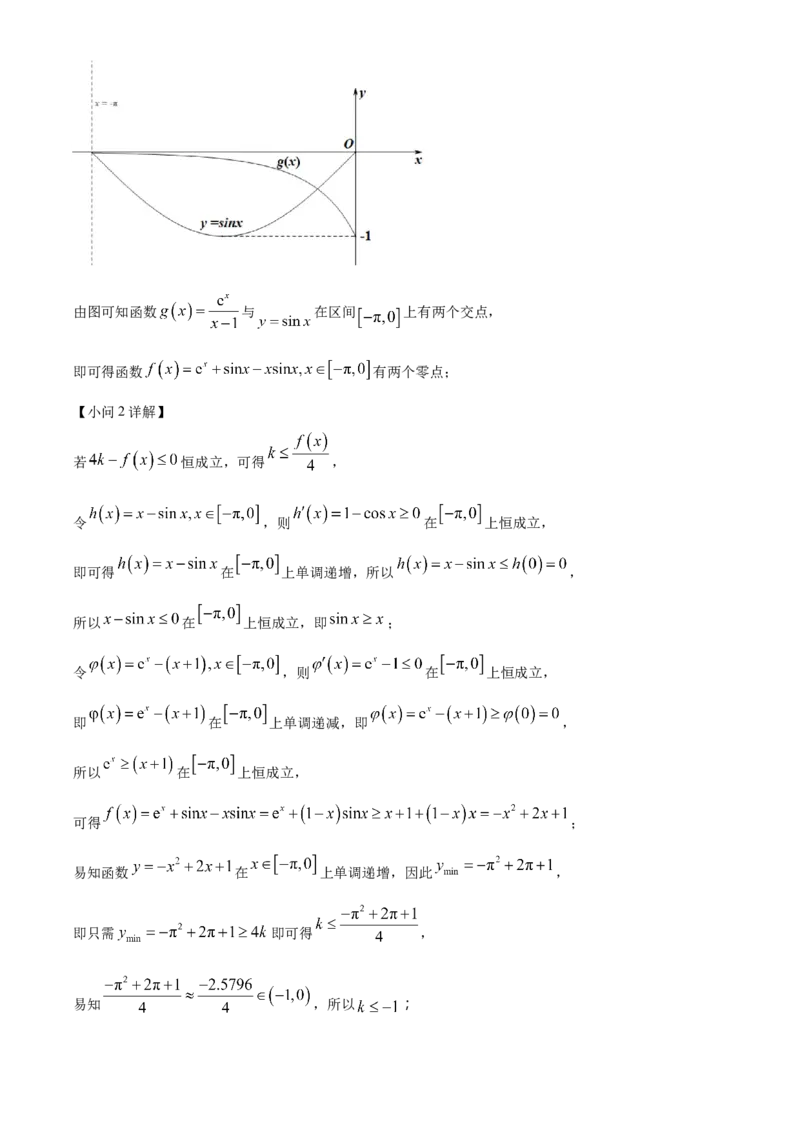
画出函数 和函数 在同一坐标系下的图象如下图所示:由图可知函数 与 在区间 上有两个交点,
即可得函数 有两个零点;
【小问2详解】
若 恒成立,可得 ,
令 ,则 在 上恒成立,
即可得 在 上单调递增,所以 ,
所以 在 上恒成立,即 ;
令 ,则 在 上恒成立,
即 在 上单调递减,即 ,
所以 在 上恒成立,
可得 ;
易知函数 在 上单调递增,因此 ,
即只需 即可得 ,
易知 ,所以 ;注意到,由(1)可知,由 有两个零点可知,必存在 ,使得 ,
所以当 时, ,故 不恒成立;
综上,整数 的最大值为 .
22. 已知函数 有三个极值点 ,且 .
(1)求实数 的取值范围;
(2)若2是 的一个极大值点,证明: .
【答案】(1)
(2)证明见解析;
【解析】
【分析】(1)利用函数极值点个数可得 在 上至少有三个实数根,即可知
在 有两个不等于2的不相等的实数根;利用导数求出 的单调性并
在同一坐标系下画出函数 与函数 的图象即可求得实数 的取值范围;
(2)根据(1)中的结论可得 ,将要证明的不等式化为 ,利用分析法可得需证明 ,
由 的单调性可知 ,化简可得 ,构造函数
即可得出证明.
【小问1详解】
根据题意可知,函数 的定义域为 ,则 ,
由函数 有三个极值点 可知 在 上至少有三个实数根;
显然 ,则需方程 ,也即 有两个不等于2 的不相等的实数根;
由 可得 , ,
令 ,则 ,
显然当 时, ,即 在 上单调递减;
当 时, ,即 在 上单调递增;
所以 ,
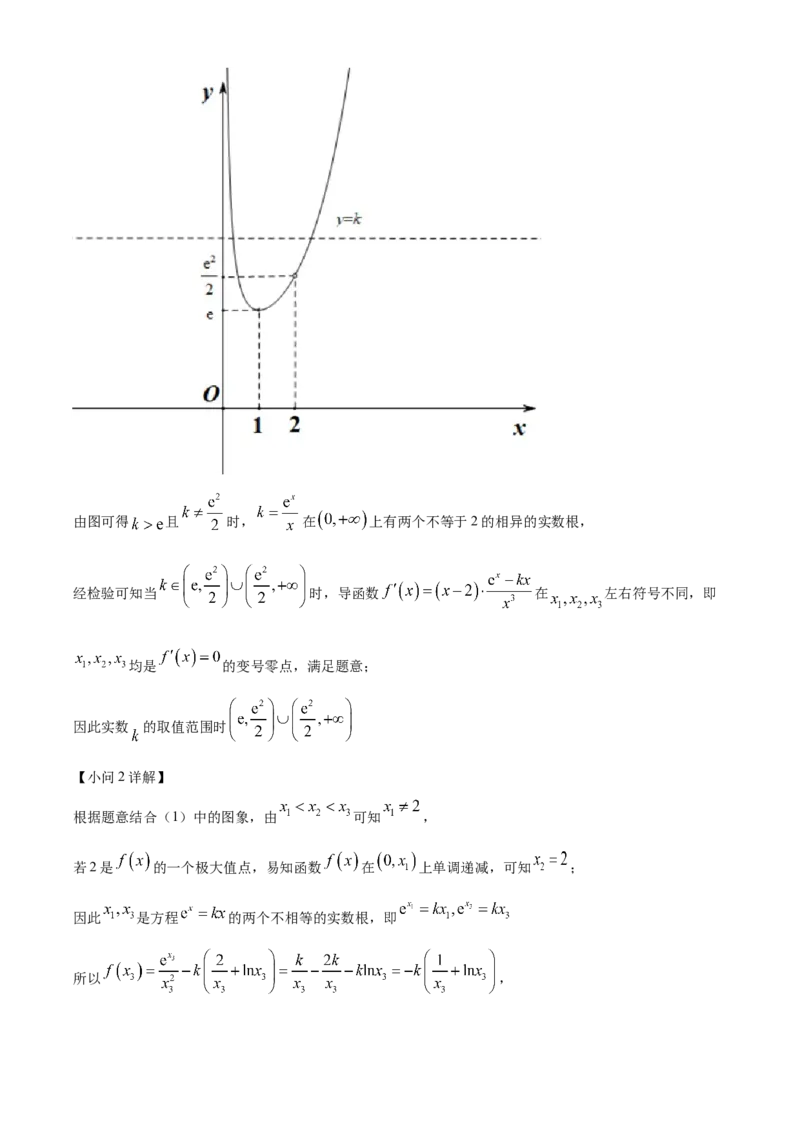
画出函数 与函数 在同一坐标系下的图象如下图所示:由图可得 且 时, 在 上有两个不等于2的相异的实数根,
经检验可知当 时,导函数 在 左右符号不同,即
均是 的变号零点,满足题意;
因此实数 的取值范围时
【小问2详解】
根据题意结合(1)中的图象,由 可知 ,
若2是 的一个极大值点,易知函数 在 上单调递减,可知 ;
因此 是方程 的两个不相等的实数根,即
所以 ,同理可得 ,
所以
由 可知 ,
所以
又 ,要证 ,
即证 ,也即 ,所以 ;
只需证 ,即 可得 ;
由(1)可得 ,所以可得 ,
且根据(1)中结论可知函数 在 上单调递减;
所以要证证 ,即证 ,又 ,即 ,
即证 ,即 ,
可得 ,即 ,可得 ,
令 ,则 ,令 ,则 ,所以 在 上单调递减,
即 ,所以 ,即 在 上单调递减;
因此 ,即可得证.
【点睛】方法点睛:在处理函数极值点问题时,是将极值点转化成导函数的变号零点,利用函数与方程的
思想转化为图像交点个数的问题;双变量问题一般是通过已有的等量关系或者构造函数转化为单变量问题,
利用单调性求解即可.