文档内容
天津一中 2024—2025—1 高三年级第二次月考数学试卷
本试卷总分150分,考试用时120分钟.考生务必将答案涂写在答题卡上,答在试卷上的无效.
一、选择题(本大题共9小题,每小题5分,共45分)
1. 已知全集 ,若 ,则集合 ( )
.
A B. C. D.
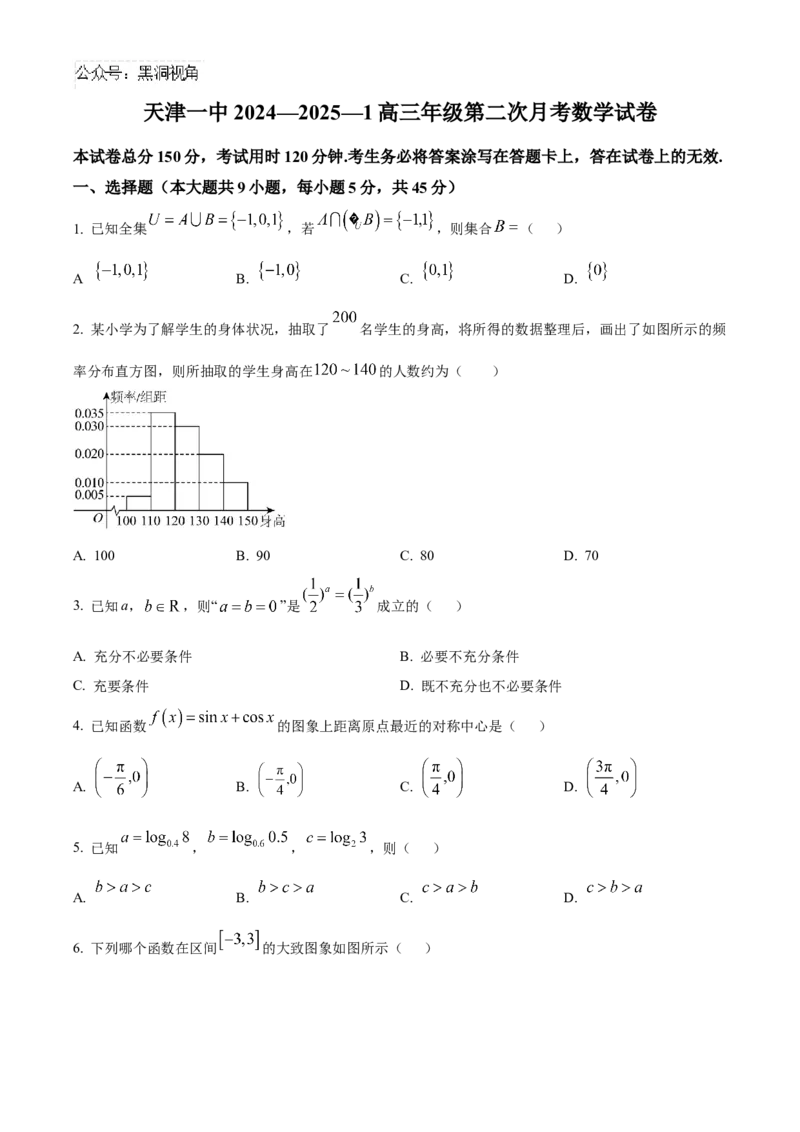
2. 某小学为了解学生的身体状况,抽取了 名学生的身高,将所得的数据整理后,画出了如图所示的频
率分布直方图,则所抽取的学生身高在 的人数约为( )
A. 100 B. 90 C. 80 D. 70
3. 已知a, ,则“ ”是 成立的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
4. 已知函数 的图象上距离原点最近的对称中心是( )
A. B. C. D.
5. 已知 , , ,则( )
A. B. C. D.
6. 下列哪个函数在区间 的大致图象如图所示( )A. B.
C. D.
7. 已知椭圆 的右顶点A,右焦点F,经过A、F两点的圆C与y轴相切于点 ,则圆C
被直线AB截得的弦长为( )
A. B. C. D.
8. 如图,三棱柱 中, 是 上靠近 的三等分点,平面 将三棱柱分成体积为 ,
两部分,则 ( )
A. B. C. D.
9. 在无穷数列 中, , ,数列 的前n项和为 ,则 的最大
值与最小值的差为( )
A. B..
C D. 无法确定
二、填空题(本大题共6小题,每小题5分,共30分)
10. 已知 是虚数单位,复数 ________.
11. 在二项式 展开式中,常数项为______.
的
12. 在等差数列 中,数列 的前n项和为 , , ,若
,则 的最小值为________.
的
13. 现有7张卡片,分别写上数字1,2,2,3,4,5,6.则这7个数 第75百分数是________;从这7张
卡片中随机抽取2张,则所抽取卡片上数字的最小值为2的概率________.
14. 已知边长为2的菱形ABCD, ,若O为菱形ABCD中心,E为BC中点,记 ,
,则 ________(结果用 , 表示);若P是菱形ABCD及其内部的一点且满足
,则动点P所在的曲线长度为________.
15. 若函数 恰有两个零点,则a的取值范围为________.
三、解答题(本大题共5小题,共75分)
16. 在 中,内角 的对边分别为 ,且 , .
(1)求 的值;
(2)求 的值;
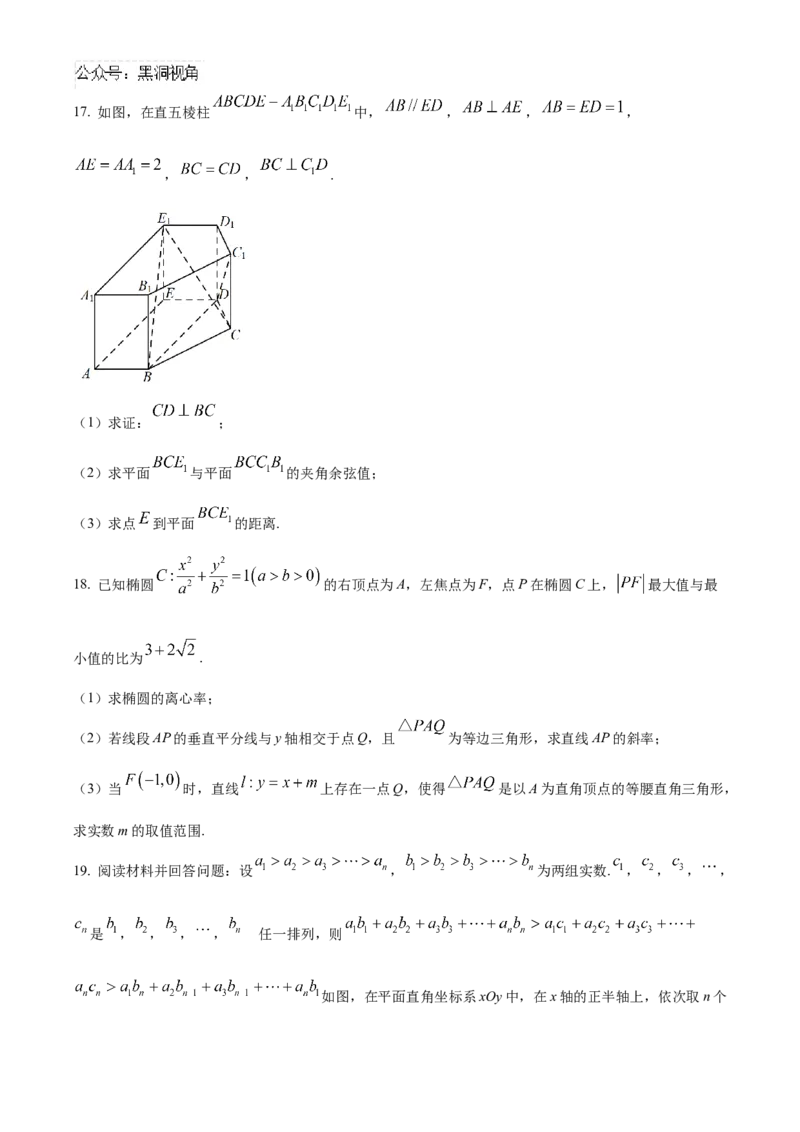
(3)求 的值.17. 如图,在直五棱柱 中, , , ,
, , .
(1)求证: ;
(2)求平面 与平面 的夹角余弦值;
(3)求点 到平面 的距离.
18. 已知椭圆 的右顶点为A,左焦点为F,点P在椭圆C上, 最大值与最
小值的比为 .
(1)求椭圆的离心率;
(2)若线段AP的垂直平分线与y轴相交于点Q,且 为等边三角形,求直线AP的斜率;
(3)当 时,直线 上存在一点Q,使得 是以A为直角顶点的等腰直角三角形,
求实数m的取值范围.
19. 阅读材料并回答问题:设 , 为两组实数. , , , ,
的
是 , , , , 任一排列,则
如图,在平面直角坐标系xOy中,在x轴的正半轴上,依次取n个点. 、 、 ,在y轴的正半轴上依次取n个点. 、 、 ,其中 、
.已知数列 为等比数列, 为等差数列,且 , , .
(1)求 , 的通项公式;
(2)若数列 中, , ,求证: ;
(3)任意选取某两个点 与 ( ,2, ,n; ,2, ,n)连结它们,得到 ,这
样一一搭配,一共可以得到n个三角形,求这n个三角形的面积之和最小值.(结果用n表示)
20. 已知函数
(1)若对于任意的 ,都有函数 是增函数,求 的取值范围;
(2)当 , 时,若函数 有两个不同的零点 ,证明:
;
(3)当 , 时,若 且 ,证明:天津一中 2024—2025—1 高三年级第二次月考数学试卷
本试卷总分150分,考试用时120分钟.考生务必将答案涂写在答题卡上,答在试卷上的无效.
一、选择题(本大题共9小题,每小题5分,共45分)
【1题答案】
【答案】D
【2题答案】
【答案】A
【3题答案】
【答案】A
【4题答案】
【答案】B
【5题答案】
【答案】D
【6题答案】
【答案】B
【7题答案】
【答案】D
【8题答案】
【答案】C
【9题答案】
【答案】C
二、填空题(本大题共6小题,每小题5分,共30分)
【10题答案】
【答案】
【11题答案】
【答案】160
【12题答案】
【答案】17
【13题答案】【答案】 ①. 5 ②.
【14题答案】
【答案】 ①. ②.
【15题答案】
【答案】
三、解答题(本大题共5小题,共75分)
【16题答案】
【答案】(1)
(2)
(3)
【17题答案】
【答案】(1)证明见解析
(2)
(3)
【18题答案】
【答案】(1)
(2)
(3)【19题答案】
【答案】(1) , ;
(2)证明见解析; (3) .
【20题答案】
【答案】(1) (2)证明见解析 (3)证明见解析