文档内容
威远中学校 学年⾼⼆上期 ⽉⽉考
2025-2026 12
数学
2025.12.12
数学试题共4⻚,满分150分,考试时间120分钟.
注意事项:
1.答题前,务必将⾃⼰的姓名、准考证号填写在答题卡规定的位置上.
2.答选择题时,必须使⽤2B铅笔将答题卡上对应题⽬的答案标号涂⿊,如需改动,⽤橡⽪擦
擦⼲净后,再选涂其他答案标号.
3.答⾮选择题时,必须使⽤0.5毫⽶⿊⾊签字笔,将答案书写在答题卡规定的位置上.
4.所有题⽬必须在答题卡上作答,在试题卷上答题⽆效.
第Ⅰ卷(选择题,共58分)
⼀、单选题(本⼤题共8⼩题,每⼩题5分,共40分.在每⼩题给出的四个选项中,只有⼀项
符合题⽬要求).
1. 直线 的倾斜⻆为( )
A B. C. D.
2. 若直线 是圆 的⼀条对称轴,则 ( )
A. B. C.1 D.
3. 若m为直线, 为两个平⾯,则下列结论中正确的是( )
A. 若 ,则 B. 若 ,则
C. 若 ,则 D. 若 ,则
4. 如图,在⻓⽅体 中, , , , , ,
则直线 与 所成⻆的余弦值为( )
第1⻚/共5⻚
学科⽹(北京)股份有限公司A. B. C. D.
5. 在棱⻓为3的正⽅体 中, 在线段 上,且 , 为线段 上的动点,
则三棱锥 的体积为( )
A.1 B. C. D. 与 点的位置有关
6. 已知 为等腰直⻆三⻆形,AB为斜边, 为等边三⻆形,若⼆⾯⻆ 为 ,则
直线CD与平⾯ABC所成⻆的正切值为( )
A. B. C. D.
7. 已知圆 上到直线 的距离为1的点有且仅有2个,则r的取值范围是
( )
A. B. C. D.
8. 已知⊙M: ,直线 : , 为 上的动点,过点 作⊙M的切线
,切点为 ,当 最⼩时,直线 的⽅程为( )
A. B. C. D.
⼆、多选题(本⼤题共3⼩题,每⼩题6分,共18分.在每⼩题给出的选项中,有多项符合题
⽬要求,全部选对的得6分,部分选对的得部分分,有选错的得0分).
9. 已知 的三个顶点的坐标分别为 , , ,则下列说法正确的有( )
A. 边上的⾼所在直线的⽅程 ;
B. 外接圆的⽅程为 ;
C. 过 作直线 与线段 相交,则直线 斜率的取值范围为 ;
D. 的⾯积为 .
10. 已知直线 与圆 ,点 ,则下列说法正确 是( )
A. 若点A在圆C上,则直线l与圆C相切 B. 若点A在圆C内,则直线l与圆C相离
第2⻚/共5⻚
学科⽹(北京)股份有限公司C. 若点A在圆C外,则直线l与圆C相离 D. 若点A在直线l上,则直线l与圆C相切
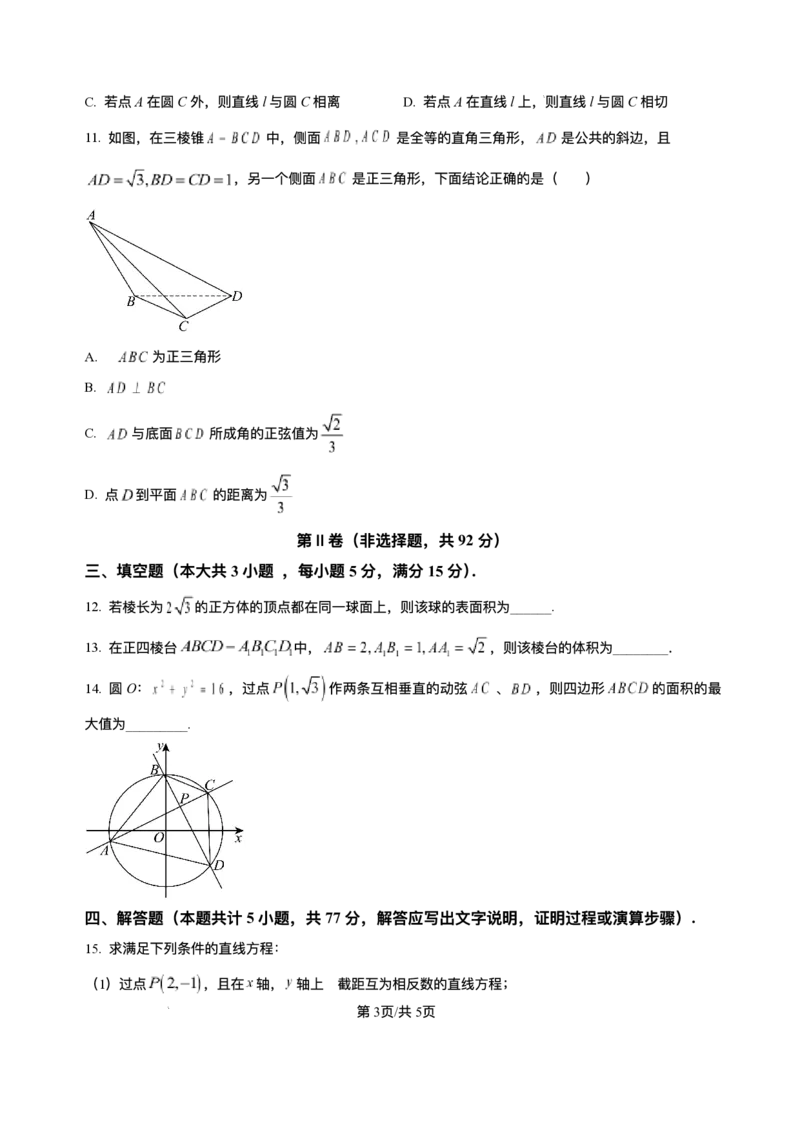
11. 如图,在三棱锥 中,侧⾯ 是全等的直⻆三⻆形, 是公共的斜边,且
,另⼀个侧⾯ 是正三⻆形,下⾯结论正确的是( )
A. 为正三⻆形
B.
C. 与底⾯ 所成⻆的正弦值为
D. 点 到平⾯ 的距离为
第Ⅱ卷(⾮选择题,共92分)
三、填空题(本⼤共3⼩题 ,每⼩题5分,满分15分).
12. 若棱⻓为 的正⽅体的顶点都在同⼀球⾯上,则该球的表⾯积为______.
13. 在正四棱台 中, ,则该棱台的体积为________.
14. 圆O: ,过点 作两条互相垂直的动弦 、 ,则四边形 的⾯积的最
⼤值为_________.
四、解答题(本题共计5⼩题,共77分,解答应写出⽂字说明,证明过程或演算步骤).
15. 求满⾜下列条件的直线⽅程:
(1)过点 ,且在 轴, 轴上 截距互为相反数的直线⽅程;
第3⻚/共5⻚
学科⽹(北京)股份有限公司(2)已知两直线 ,求过两直线的交点,且平⾏于直线 的
直线⽅程.
16 已知圆 .
(1)求m的取值范围.
(2)已知直线 与圆 交于 两点,且 .
①求 ;
②求过点 的圆 的切线⽅程.
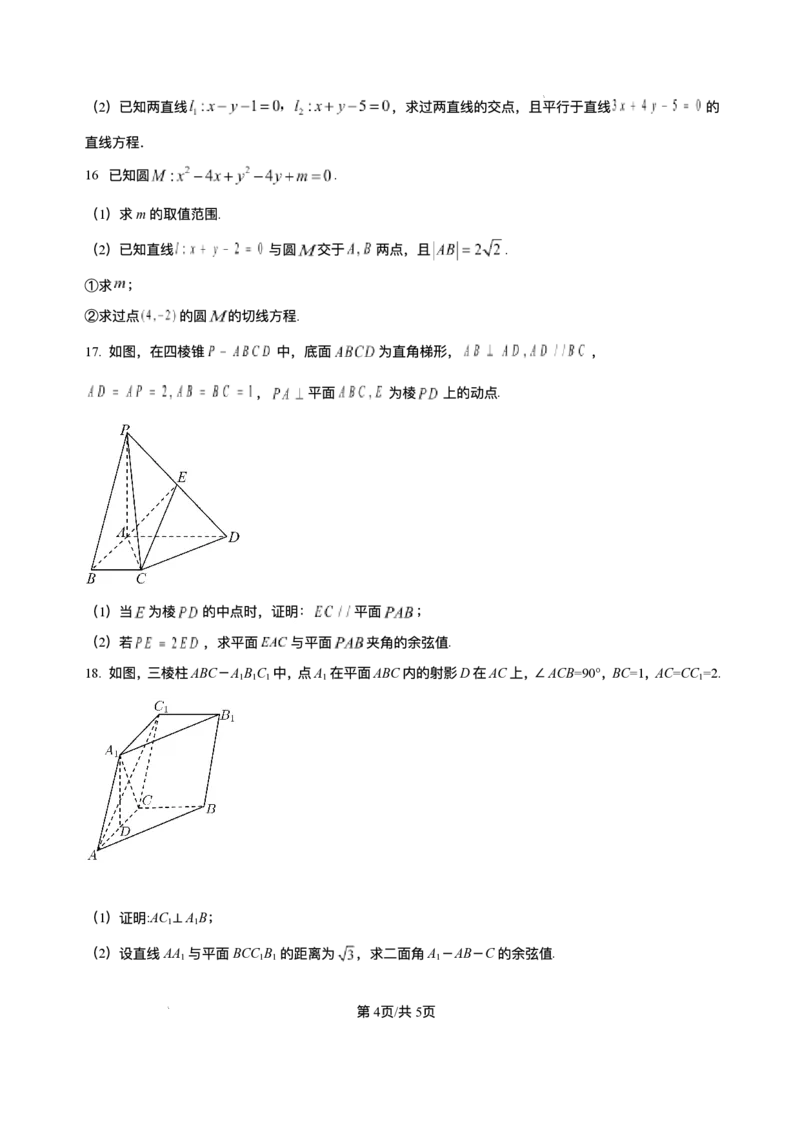
17. 如图,在四棱锥 中,底⾯ 为直⻆梯形, ,
, 平⾯ 为棱 上的动点.
(1)当 为棱 的中点时,证明: 平⾯ ;
(2)若 ,求平⾯ 与平⾯ 夹⻆的余弦值.
18. 如图,三棱柱ABC-A B C 中,点A 在平⾯ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC =2.
1 1 1 1 1
(1)证明:AC ⊥A B;
1 1
(2)设直线AA 与平⾯BCC B 的距离为 ,求⼆⾯⻆A -AB-C的余弦值.
1 1 1 1
第4⻚/共5⻚
学科⽹(北京)股份有限公司19. 已知圆 的圆⼼在直线 上,且经过点 和 .
(1)求圆 的标准⽅程;
(2)设点 在 上运动,且点 满⾜ ( 为原点),记点 的轨迹为 .
①求曲线 的⽅程;
②过点 的直线与曲线 交于 、 两点,问在 轴正半轴上是否存在定点 ,使得 轴平分
?若存在,求出点 的坐标;若不存在,请说明理由.
第5⻚/共5⻚
学科⽹(北京)股份有限公司威远中学校 学年⾼⼆上期 ⽉⽉考
2025-2026 12
数学
2025.12.12
数学试题共4⻚,满分150分,考试时间120分钟.
注意事项:
1.答题前,务必将⾃⼰的姓名、准考证号填写在答题卡规定的位置上.
2.答选择题时,必须使⽤2B铅笔将答题卡上对应题⽬的答案标号涂⿊,如需改动,⽤橡⽪擦
擦⼲净后,再选涂其他答案标号.
3.答⾮选择题时,必须使⽤0.5毫⽶⿊⾊签字笔,将答案书写在答题卡规定的位置上.
4.所有题⽬必须在答题卡上作答,在试题卷上答题⽆效.
第Ⅰ卷(选择题,共58分)
⼀、单选题(本⼤题共8⼩题,每⼩题5分,共40分.在每⼩题给出的四个选项中,只有⼀项
符合题⽬要求).
1. 直线 的倾斜⻆为( )
A. B. C. D.
【答案】B
【解析】
【分析】⾸先求斜率,再求倾斜⻆.
【详解】由条件可知,直线的斜率 ,设直线的倾斜⻆为 ,
则 , ,所以 .
故选:B
2. 若直线 是圆 的⼀条对称轴,则 ( )
A. B. C.1 D.
【答案】A
【解析】
【分析】若直线是圆的对称轴,则直线过圆⼼,将圆⼼代⼊直线计算求解.
【详解】由题可知圆⼼为 ,因为直线是圆的对称轴,所以圆⼼在直线上,即 ,解得
第1⻚/共21⻚
学科⽹(北京)股份有限公司.
故选:A.
3. 若m为直线, 为两个平⾯,则下列结论中正确的是( )
A. 若 ,则 B. 若 ,则
C. 若 ,则 D. 若 ,则
【答案】C
【解析】
【分析】根据线⾯平⾏的定义可判断A的正误,根据空间中垂直关系的转化可判断BCD的正误.
【详解】对于A,若 ,则 可平⾏或异⾯,故A错误;
对于B,若 ,则 ,故B错误;
对于C,若 ,则存在直线 , ,
所以由 可得 ,故 ,故C正确;
对于D, ,则 与 可平⾏或相交或 ,故D错误;
故选:C.
4. 如图,在⻓⽅体 中, , , , , ,
则直线 与 所成⻆的余弦值为( )
A. B. C. D.
【答案】B
【解析】
【分析】取 上靠近 的三等分点F,取 上三等分点 ,可知直线 与 所成⻆即为直线
第2⻚/共21⻚
学科⽹(北京)股份有限公司与 所成⻆,求出 ,在 中,由余弦定理求解即可.
【详解】取 上靠近 的三等分点F,取 上三等分点 ,
连接 ,
因为 ,所以四边形 是平⾏四边形,
所以 ,所以直线 与 所成⻆即为直线 与 所成⻆,
,
由正⽅体的性质可得: 平⾯ , 平⾯ ,
所以 平⾯ ,所以 , ,
, ,
,
在 中, ,
所以直线 与 所成⻆的余弦值为 .
故选:B.
5. 在棱⻓为3的正⽅体 中, 在线段 上,且 , 为线段 上的动点,
则三棱锥 的体积为( )
A.1 B. C. D. 与 点的位置有关
【答案】B
【解析】
【分析】作出图像,观察可知 ,点P到平⾯ 的距离是 到平⾯ 距离的 ,
为定值,据此即可求出体积.
第3⻚/共21⻚
学科⽹(北京)股份有限公司【详解】∵ ,
∴点P到平⾯ 的距离是 到平⾯ 距离的 ,即为 =1.
,
= × ×1= .
故选:B.
6. 已知 为等腰直⻆三⻆形,AB为斜边, 为等边三⻆形,若⼆⾯⻆ 为 ,则
直线CD与平⾯ABC所成⻆的正切值为( )
A. B. C. D.
【答案】C
【解析】
【分析】根据给定条件,推导确定线⾯⻆,再利⽤余弦定理、正弦定理求解作答.
【详解】取 的中点 ,连接 ,因为 是等腰直⻆三⻆形,且 为斜边,则有
,
⼜ 是等边三⻆形,则 ,从⽽ 为⼆⾯⻆ 的平⾯⻆,即 ,
第4⻚/共21⻚
学科⽹(北京)股份有限公司显然 平⾯ ,于是 平⾯ ,⼜ 平⾯ ,
因此平⾯ 平⾯ ,显然平⾯ 平⾯ ,
直线 平⾯ ,则直线 在平⾯ 内的射影为直线 ,
从⽽ 为直线 与平⾯ 所成的⻆,令 ,则 ,在 中,由余弦定
理得:
,
由正弦定理得 ,即 ,
显然 是锐⻆, ,
所以直线 与平⾯ 所成的⻆的正切为 .
故选:C
7. 已知圆 上到直线 的距离为1的点有且仅有2个,则r的取值范围是
( )
A. B. C. D.
【答案】B
【解析】
【分析】先求出圆⼼ 到直线 的距离,然后结合图象,即可得出结论.
【详解】由题意,
在圆 中,圆⼼ ,半径为 ,
到直线 的距离为 的点有且仅有 个,
∵圆⼼ 到直线 的距离为: ,
第5⻚/共21⻚
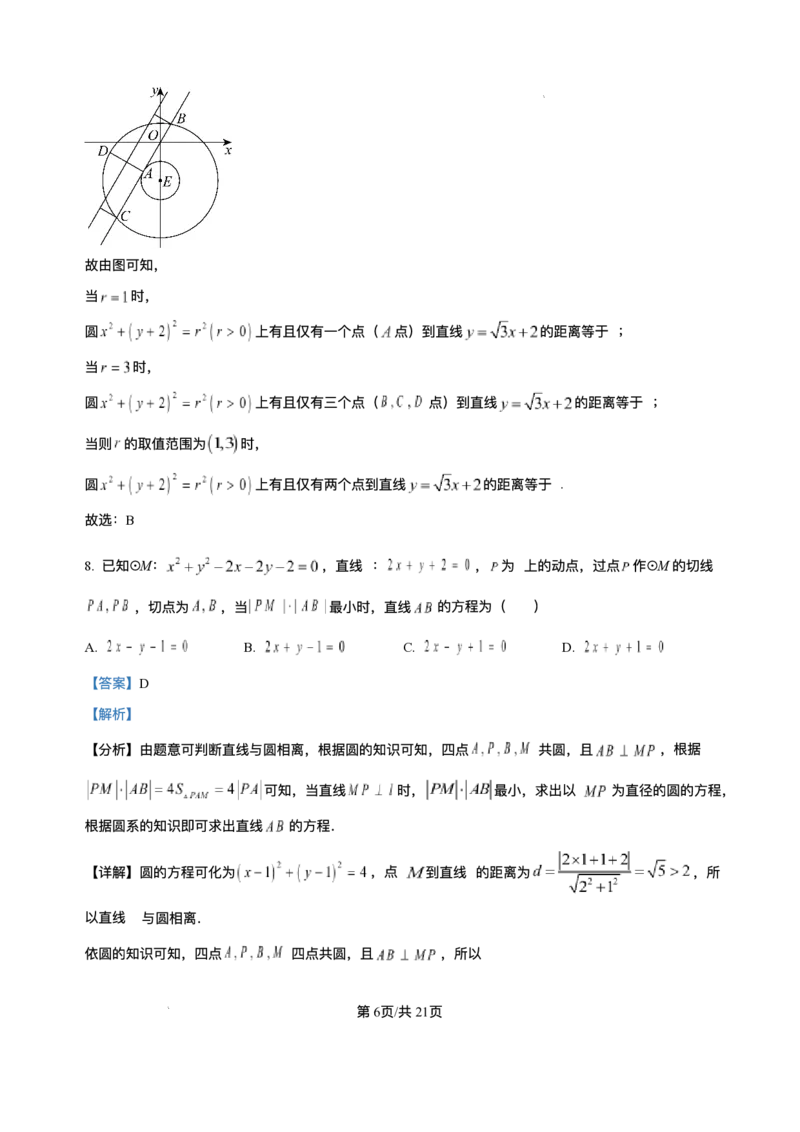
学科⽹(北京)股份有限公司故由图可知,
当 时,
圆 上有且仅有⼀个点( 点)到直线 的距离等于 ;
当 时,
圆 上有且仅有三个点( 点)到直线 的距离等于 ;
当则 的取值范围为 时,
圆 上有且仅有两个点到直线 的距离等于 .
故选:B
8. 已知⊙M: ,直线 : , 为 上的动点,过点 作⊙M的切线
,切点为 ,当 最⼩时,直线 的⽅程为( )
A. B. C. D.
【答案】D
【解析】
【分析】由题意可判断直线与圆相离,根据圆的知识可知,四点 共圆,且 ,根据
可知,当直线 时, 最⼩,求出以 为直径的圆的⽅程,
根据圆系的知识即可求出直线 的⽅程.
【详解】圆的⽅程可化为 ,点 到直线 的距离为 ,所
以直线 与圆相离.
依圆的知识可知,四点 四点共圆,且 ,所以
第6⻚/共21⻚
学科⽹(北京)股份有限公司,⽽ ,
当直线 时, , ,此时 最⼩.
∴ 即 ,由 解得, .
所以以 为直径的圆的⽅程为 ,即 ,
两圆的⽅程相减可得: ,即为直线 的⽅程.
故选:D.
【点睛】本题主要考查直线与圆,圆与圆的位置关系的应⽤,以及圆的⼏何性质的应⽤,意在考查学⽣的
转化能⼒和数学运算能⼒,属于中档题.
⼆、多选题(本⼤题共3⼩题,每⼩题6分,共18分.在每⼩题给出的选项中,有多项符合题
⽬要求,全部选对的得6分,部分选对的得部分分,有选错的得0分).
9. 已知 的三个顶点的坐标分别为 , , ,则下列说法正确的有( )
A. 边上的⾼所在直线的⽅程 ;
B. 的外接圆的⽅程为 ;
C. 过 作直线 与线段 相交,则直线 斜率的取值范围为 ;
D. 的⾯积为 .
【答案】BCD
【解析】
【分析】对选项 ,利⽤直线垂直时斜率的关系可求得⾼线⽅程;对选项 ,⽤待定系数求圆的⽅程;对
选项 ,根据直线 从点 到点 的过程中斜率的变化求得;对选项 , 的⾯积利⽤点到直线的距
离求得 中 边的⾼,然后根据⾯积公式即可.
【详解】对选项 ,直线 的斜率为:
则 边上的⾼的斜率为:
则⾼的⽅程为: ,即
故 不正确;
第7⻚/共21⻚
学科⽹(北京)股份有限公司对选项 ,设 外接圆的⽅程为
则有:
解得: , ,
所以△ 的外接圆的⽅程为:
故 正确;
对选项 , ,
则过点 作直线 与线段 相交时,则直线 斜率的取值范围为:
故 正确;
对选项 ,易知 所在直线的⽅程为:
点 到直线 的距离为:
⼜
则 的⾯积为:
故 正确
故选:
10. 已知直线 与圆 ,点 ,则下列说法正确的是( )
A. 若点A在圆C上,则直线l与圆C相切 B. 若点A在圆C内,则直线l与圆C相离
C. 若点A在圆C外,则直线l与圆C相离 D. 若点A在直线l上,则直线l与圆C相切
【答案】ABD
【解析】
【分析】转化点与圆、点与直线的位置关系为 的⼤⼩关系,结合点到直线的距离及直线与圆的位
置关系即可得解.
【详解】圆⼼ 到直线l的距离 ,
第8⻚/共21⻚
学科⽹(北京)股份有限公司若点 在圆C上,则 ,所以 ,
则直线l与圆C相切,故A正确;
若点 在圆C内,则 ,所以 ,
则直线l与圆C相离,故B正确;
若点 在圆C外,则 ,所以 ,
则直线l与圆C相交,故C错误;
若点 在直线l上,则 即 ,
所以 ,直线l与圆C相切,故D正确.
故选:ABD.
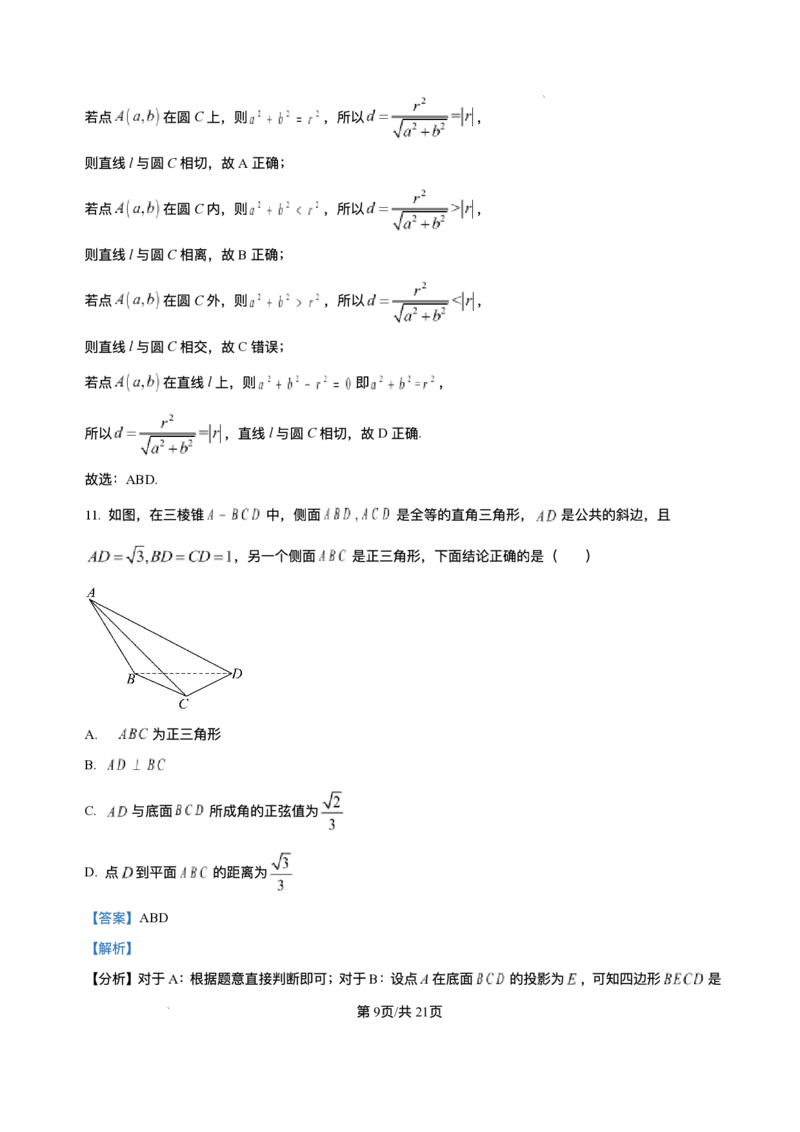
11. 如图,在三棱锥 中,侧⾯ 是全等的直⻆三⻆形, 是公共的斜边,且
,另⼀个侧⾯ 是正三⻆形,下⾯结论正确的是( )
A. 为正三⻆形
B.
C. 与底⾯ 所成⻆的正弦值为
D. 点 到平⾯ 的距离为
【答案】ABD
【解析】
【分析】对于A:根据题意直接判断即可;对于B:设点A在底⾯ 的投影为 ,可知四边形 是
第9⻚/共21⻚
学科⽹(北京)股份有限公司边⻓为1的正⽅形,进⽽可证 平⾯ ,即可得结果;对于C:可知 与底⾯ 所成⻆为
,进⽽求解;对于D:转换顶点结合等体积法求点到⾯的距离即可.
【详解】对于选项A:因为侧⾯ 是正三⻆形,故A正确;
对于选项B:由题意可知: , ,
则 ,可知 .
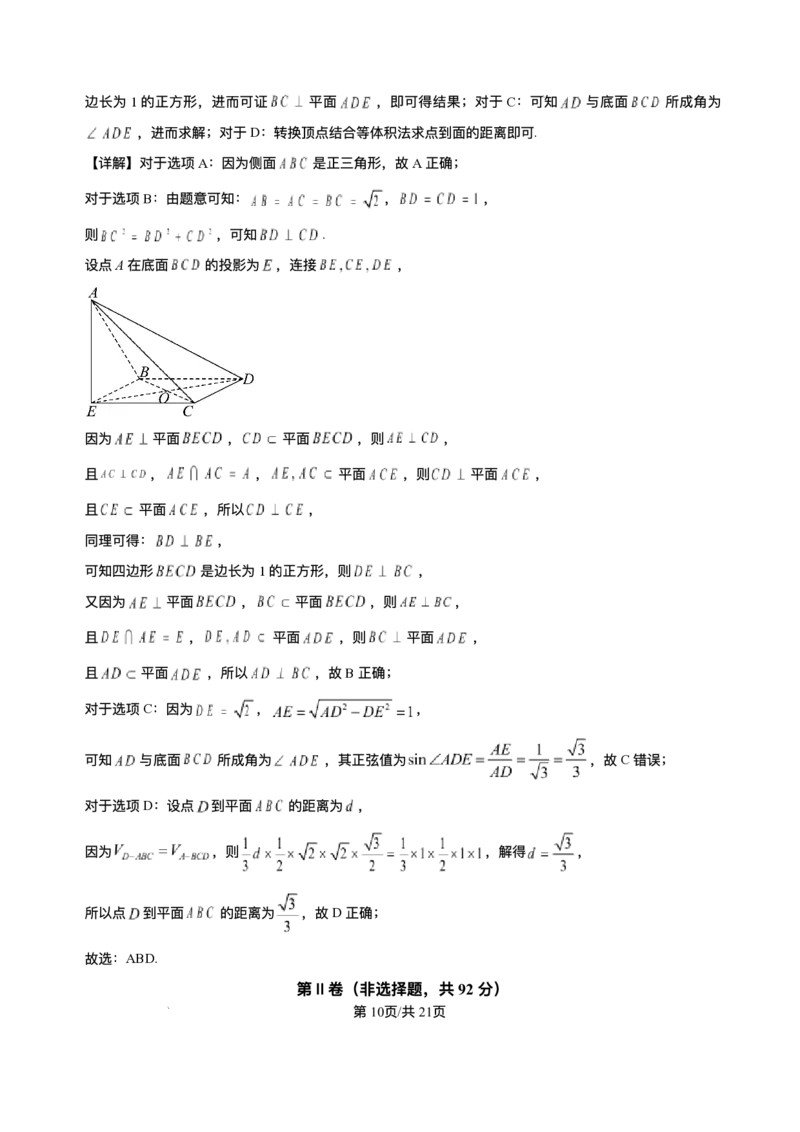
设点A在底⾯ 的投影为 ,连接 ,
因为 平⾯ , 平⾯ ,则 ,
且 , , 平⾯ ,则 平⾯ ,
且 平⾯ ,所以 ,
同理可得: ,
可知四边形 是边⻓为1的正⽅形,则 ,
⼜因为 平⾯ , 平⾯ ,则 ,
且 , 平⾯ ,则 平⾯ ,
且 平⾯ ,所以 ,故B正确;
对于选项C:因为 , ,
可知 与底⾯ 所成⻆为 ,其正弦值为 ,故C错误;
对于选项D:设点 到平⾯ 的距离为 ,
因为 ,则 ,解得 ,
所以点 到平⾯ 的距离为 ,故D正确;
故选:ABD.
第Ⅱ卷(⾮选择题,共92分)
第10⻚/共21⻚
学科⽹(北京)股份有限公司三、填空题(本⼤共3⼩题 ,每⼩题5分,满分15分).
12. 若棱⻓为 的正⽅体的顶点都在同⼀球⾯上,则该球的表⾯积为______.
【答案】 .
【解析】
【分析】求出球的半径即可.
【详解】解:因为正⽅体的顶点都在同⼀球⾯上,
所以球的直径为正⽅体的对⻆线,
所以 ,
所以 ,
故球的表⾯积: .
故答案 : .
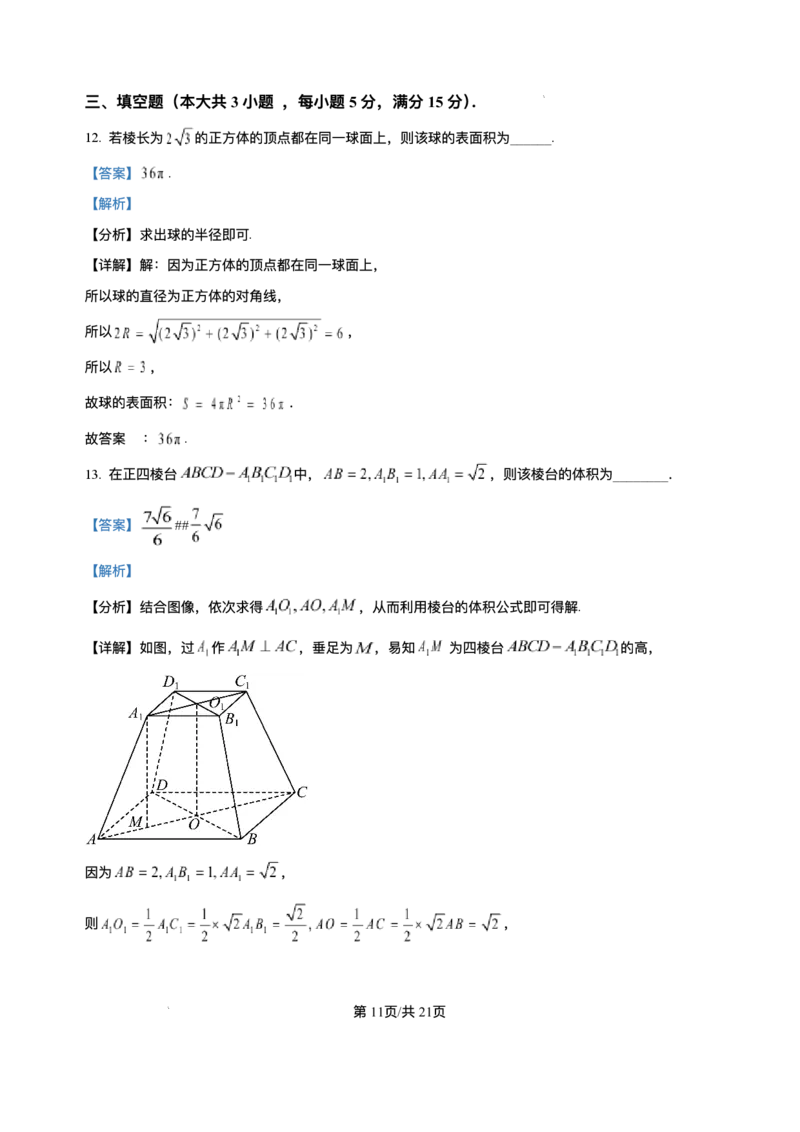
13. 在正四棱台 中, ,则该棱台的体积为________.
【答案】 ##
【解析】
【分析】结合图像,依次求得 ,从⽽利⽤棱台的体积公式即可得解.
【详解】如图,过 作 ,垂⾜为 ,易知 为四棱台 的⾼,
因为 ,
则 ,
第11⻚/共21⻚
学科⽹(北京)股份有限公司故 ,则 ,
所以所求体积为 .
故答案为: .
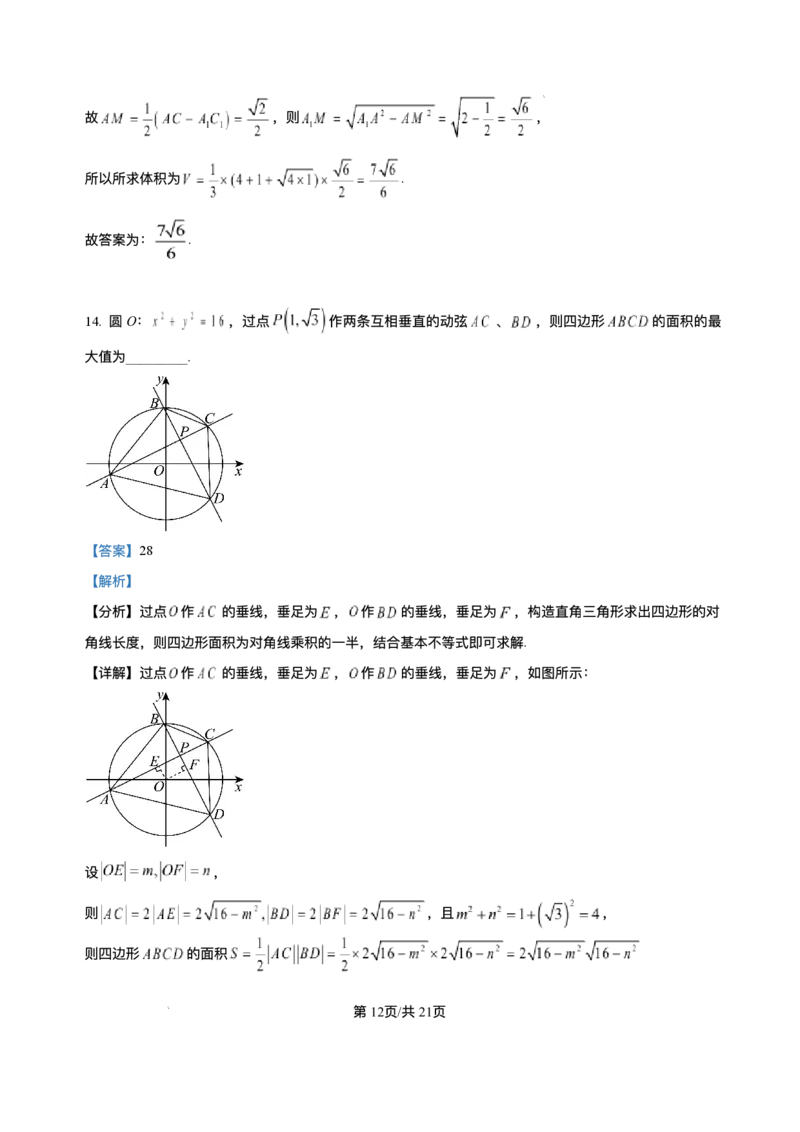
14. 圆O: ,过点 作两条互相垂直的动弦 、 ,则四边形 的⾯积的最
⼤值为_________.
【答案】28
【解析】
【分析】过点 作 的垂线,垂⾜为 , 作 的垂线,垂⾜为 ,构造直⻆三⻆形求出四边形的对
⻆线⻓度,则四边形⾯积为对⻆线乘积的⼀半,结合基本不等式即可求解.
【详解】过点 作 的垂线,垂⾜为 , 作 的垂线,垂⾜为 ,如图所示:
设 ,
则 ,且 ,
则四边形 的⾯积
第12⻚/共21⻚
学科⽹(北京)股份有限公司,
当且仅当 ,即 时,等号成⽴,
所以四边形 的⾯积的最⼤值为28.
故答案为:28.
四、解答题(本题共计5⼩题,共77分,解答应写出⽂字说明,证明过程或演算步骤).
15. 求满⾜下列条件的直线⽅程:
(1)过点 ,且在 轴, 轴上的截距互为相反数的直线⽅程;
(2)已知两直线 ,求过两直线的交点,且平⾏于直线 的
直线⽅程.
【答案】(1) 或
(2)
【解析】
【分析】(1)分两种情况,过原点时设直线⽅程为 ,不过原点时设直线⽅程为 ,代⼊点
即可求解;
(2)联⽴ 、 ,解出交点坐标,再结合与直线 平⾏,利⽤点斜式即可求解.
【⼩问1详解】
分两种情况,
当直线过原点时,设 ,代⼊ ,得 ,⽅程为 ,
当直线不过原点时,设截距式 ,代⼊ ,得 ,⽅程为 ,
综上,直线⽅程为 或 .
【⼩问2详解】
联⽴ 、 ⽅程 ,解得交点为 ,
直线 斜率为 ,所求直线与之平⾏,斜率也为 ,⼜因为过 ,
第13⻚/共21⻚
学科⽹(北京)股份有限公司所以直线⽅程为 ,
整理得 .
16. 已知圆 .
(1)求m的取值范围.
(2)已知直线 与圆 交于 两点,且 .
①求 ;
②求过点 的圆 的切线⽅程.
【答案】(1)
(2)① ;② 或 .
【解析】
【分析】(1)根据圆的⼀般⽅程成⽴条件,建⽴不等式,可得答案.
(2)①根据弦⻓公式,建⽴⽅程,求出参数;②根据切线⽅程的求法,可得答案.
【⼩问1详解】
(⽅法⼀)由题意得 ,则 ,
得 ,所以 的取值范围为 .
(⽅法⼆)由 ,
得 ,所以 的取值范围为 .
【⼩问2详解】
①由题意得 到 的距离 ,
则圆 的半径为 ,
得
②当所求切线的斜率不存在时,该切线的⽅程为 .
当所求切线的斜率存在时,设该切线的⽅程为 ,即 .
第14⻚/共21⻚
学科⽹(北京)股份有限公司由 ,得 ,
所以所求的切线⽅程为 ,即 .
综上,过点 的圆 的切线⽅程为 或 .
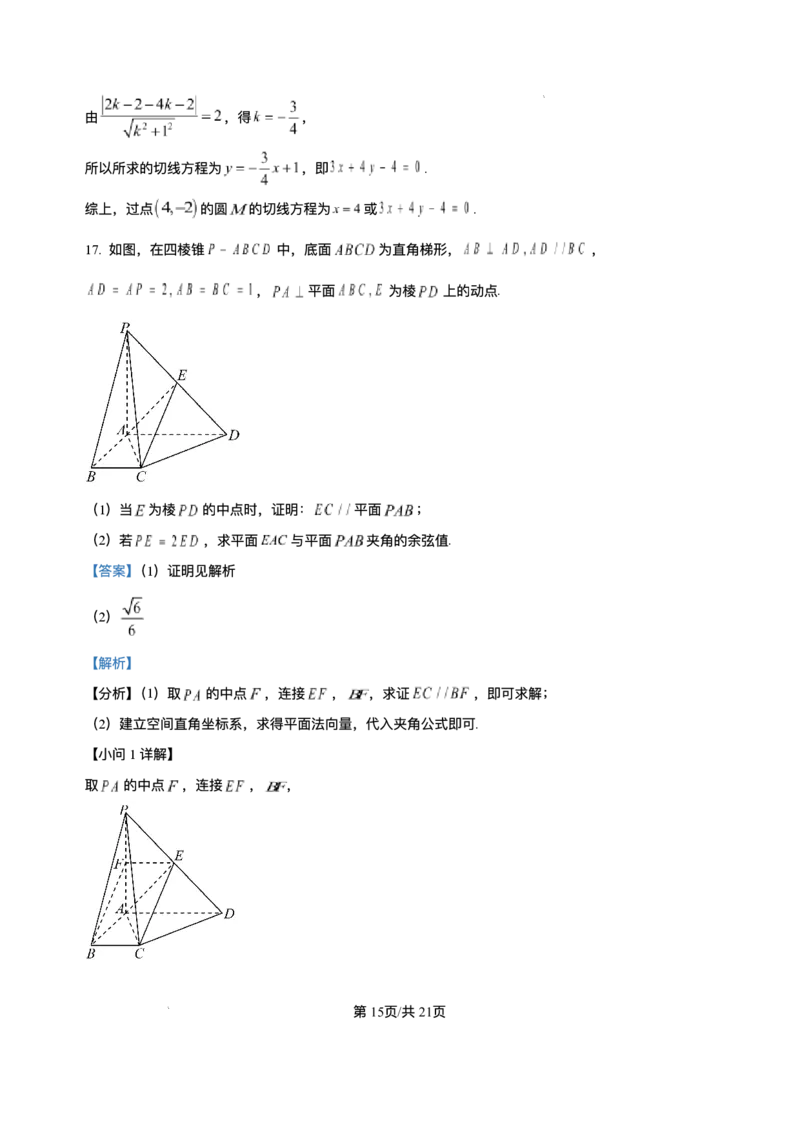
17. 如图,在四棱锥 中,底⾯ 为直⻆梯形, ,
, 平⾯ 为棱 上的动点.
(1)当 为棱 的中点时,证明: 平⾯ ;
(2)若 ,求平⾯ 与平⾯ 夹⻆的余弦值.
【答案】(1)证明⻅解析
(2)
【解析】
【分析】(1)取 的中点 ,连接 , ,求证 ,即可求解;
(2)建⽴空间直⻆坐标系,求得平⾯法向量,代⼊夹⻆公式即可.
【⼩问1详解】
取 的中点 ,连接 , ,
第15⻚/共21⻚
学科⽹(北京)股份有限公司因为 为 的中点,所以 ,
因为 ,所以 ,
所以四边形 为平⾏四边形,所以
⼜ 平⾯ 平⾯ ,所以 平⾯ .
【⼩问2详解】
因为 平⾯ ,
在平⾯ 内,所以 ,
即 两两垂直,
故可以 为原点, 所在直线分别为 轴建⽴如图所示的空间直⻆坐标系.
则
因为 ,所以 ,
所以 .
设平⾯ 的法向量为 ,
则 ,取 ,得 ,所以
因为 平⾯ ,所以 平⾯ .
所以 为平⾯ 的⼀个法向量.
设平⾯ 与平⾯ 的夹⻆为 ,
第16⻚/共21⻚
学科⽹(北京)股份有限公司则 .
所以平⾯ 与平⾯ 夹⻆的余弦值为 .
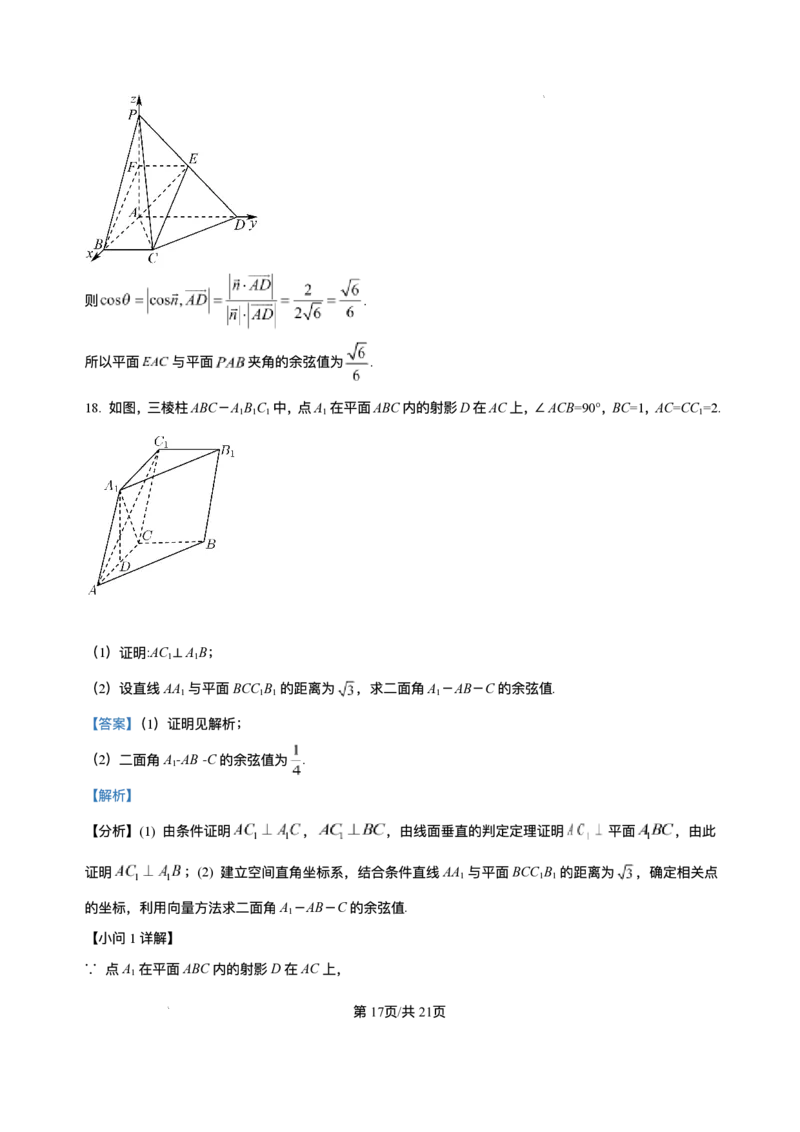
18. 如图,三棱柱ABC-A B C 中,点A 在平⾯ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC =2.
1 1 1 1 1
(1)证明:AC ⊥A B;
1 1
(2)设直线AA 与平⾯BCC B 的距离为 ,求⼆⾯⻆A -AB-C的余弦值.
1 1 1 1
【答案】(1)证明⻅解析;
(2)⼆⾯⻆A -AB -C的余弦值为 .
1
【解析】
【分析】(1) 由条件证明 , ,由线⾯垂直的判定定理证明 平⾯ ,由此
证明 ;(2) 建⽴空间直⻆坐标系,结合条件直线AA 与平⾯BCC B 的距离为 ,确定相关点
1 1 1
的坐标,利⽤向量⽅法求⼆⾯⻆A -AB-C的余弦值.
1
【⼩问1详解】
∵ 点A 在平⾯ABC内的射影D在AC上,
1
第17⻚/共21⻚
学科⽹(北京)股份有限公司∴ 平⾯ ,⼜ 平⾯ ,
∴ ,∵ , , 平⾯ ,
∴ 平⾯ , 平⾯ ,
∴ ,
∵ ,四边形 为平⾏四边形,
∴ 四边形 为菱形,故 ,
⼜ , 平⾯ ,
∴ 平⾯ , 平⾯ ,
∴ ;
⼩问2详解】
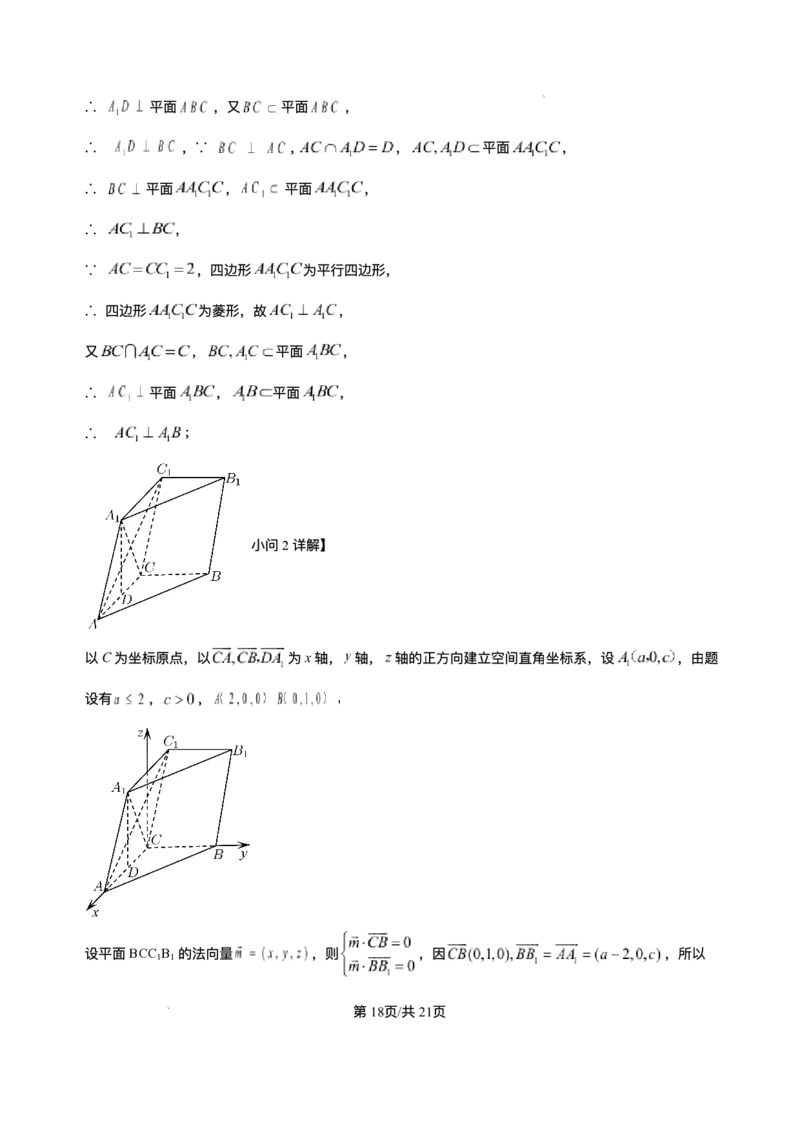
以C为坐标原点,以 为x轴, 轴, 轴的正⽅向建⽴空间直⻆坐标系,设 ,由题
设有 , ,
设平⾯BCC B 的法向量 ,则 ,因 ,所以
1 1
第18⻚/共21⻚
学科⽹(北京)股份有限公司,
所以 ,⼜ , 即 ,
所以点 到平⾯ 的距离为 ,⼜依题设,直线AA
1
与平⾯BCC B 的距离为 ,所以 .代⼊①得 (舍去)或 ,于是 ,
1 1
设平⾯ 的法向量 ,则 ,所以 ,所以 ,⼜
为平⾯ 的法向量,故 ,
所以⼆⾯⻆A -AB -C的余弦值为 .
1
19. 已知圆 的圆⼼在直线 上,且经过点 和 .
(1)求圆 的标准⽅程;
(2)设点 在 上运动,且点 满⾜ ( 为原点),记点 的轨迹为 .
①求曲线 的⽅程;
②过点 的直线与曲线 交于 、 两点,问在 轴正半轴上是否存在定点 ,使得 轴平分
?若存在,求出点 的坐标;若不存在,请说明理由.
【答案】(1)
(2)(i) ;(ii)存在,且定点为
【解析】
【分析】(1)设点 ,根据 结合两点间的距离公式求出 的值,可得出圆⼼ 的坐
标,求出圆 的半径⻓,即可得出圆 的标准⽅程;
(2)(i)设点 、 ,根据平⾯向量的坐标运算得出 ,代⼊等式
化简可得曲线 的⽅程;
第19⻚/共21⻚
学科⽹(北京)股份有限公司(ii)假设存在满⾜题设条件的点 ,设点 、 ,设直线 的⽅程为 ,
将该直线⽅程与曲线 的⽅程联⽴,列出⻙达定理,根据 求出 的值,即可得出结论.
【⼩问1详解】
因为圆⼼ 在直线 上,设点 ,
由题意得 ,即 ,解得 ,
所以圆⼼为 ,半径为 ,
故圆 的标准⽅程为 .
【⼩问2详解】
(i)设点 、 ,由 可得 ,
所以 ,解得 ,
因为点 在 上,所以 (*),
将 代⼊等式(*)得 ,即 ,
故曲线 的⽅程为 ;
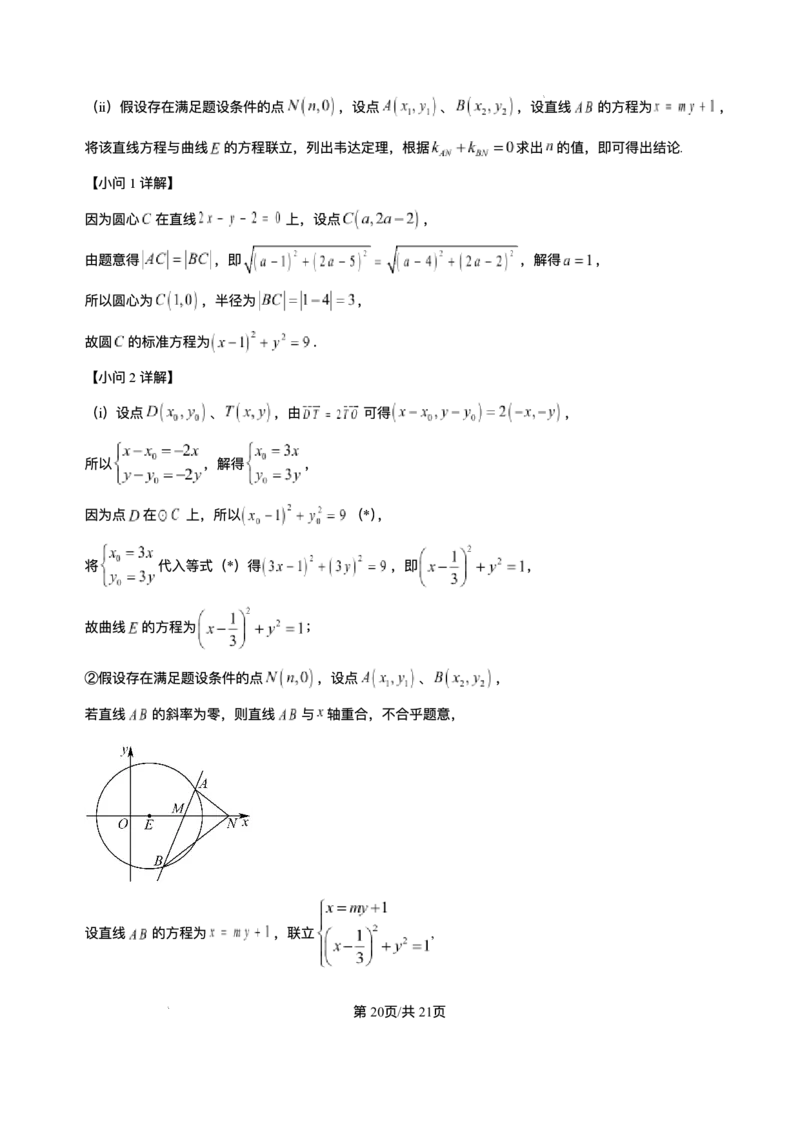
②假设存在满⾜题设条件的点 ,设点 、 ,
若直线 的斜率为零,则直线 与 轴重合,不合乎题意,
设直线 的⽅程为 ,联⽴ ,
第20⻚/共21⻚
学科⽹(北京)股份有限公司可得 ,
,
由⻙达定理可得 , ,
直线 的斜率为 ,
同理可得直线 的斜率为 ,
所以
,
即 对任意的 恒成⽴,故 ,解得 ,
故在 轴正半轴上存在定点 ,使得 轴平分 .
第21⻚/共21⻚
学科⽹(北京)股份有限公司