文档内容
成都石室中学2023-2024年度下期高2024届高考考前模拟一
数学试题(理科)
(总分:150分,时间:120分钟 )
第Ⅰ卷(共60分)
一、选择题(本题共12道小题,每小题5分,共60分)
1. 已知集合 ,若 ,则实数 的所有可能取值的集合为( )
A. B. C. D.
2. 复数 在复平面上对应的点位于虚轴上,则实数 的值为( )
A. B. C. D.
3. 已知 , 为实数,则使得“ ”成立的一个必要不充分条件为( )
A. B. C. D.
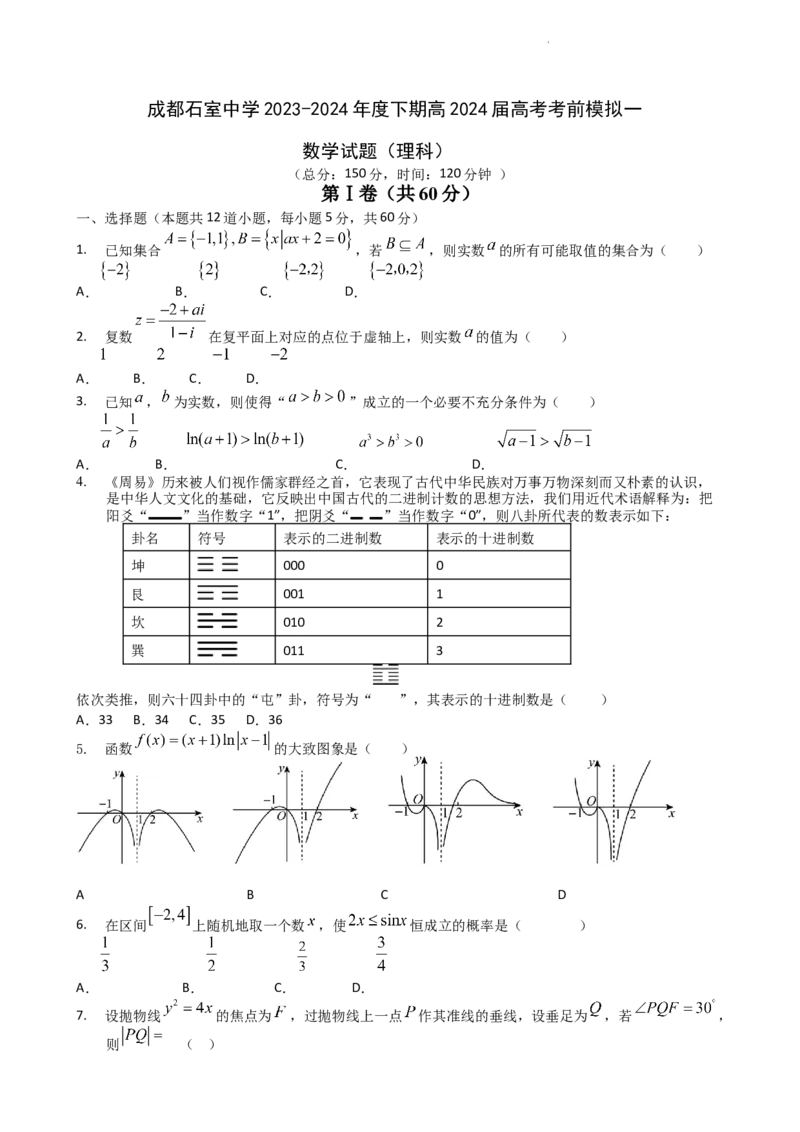
4. 《周易》历来被人们视作儒家群经之首,它表现了古代中华民族对万事万物深刻而又朴素的认识,
是中华人文文化的基础,它反映出中国古代的二进制计数的思想方法,我们用近代术语解释为:把
阳爻“ ”当作数字“1”,把阴爻“ ”当作数字“0”,则八卦所代表的数表示如下:
卦名 符号 表示的二进制数 表示的十进制数
坤 000 0
艮 001 1
坎 010 2
巽 011 3
依次类推,则六十四卦中的“屯”卦,符号为“ ”,其表示的十进制数是( )
A.33 B.34 C.35 D.36
5. 函数 的大致图象是( )
A B C D
6. 在区间 上随机地取一个数 ,使 恒成立的概率是( )
A. B. C. D.
7. 设抛物线 的焦点为 ,过抛物线上一点 作其准线的垂线,设垂足为 ,若 ,
则 ( )
学科网(北京)股份有限公司A. B. C. D.
8. 变量 , 满足约束条件 ,则目标函数 的取值范围是( ).
A. B. C. D.
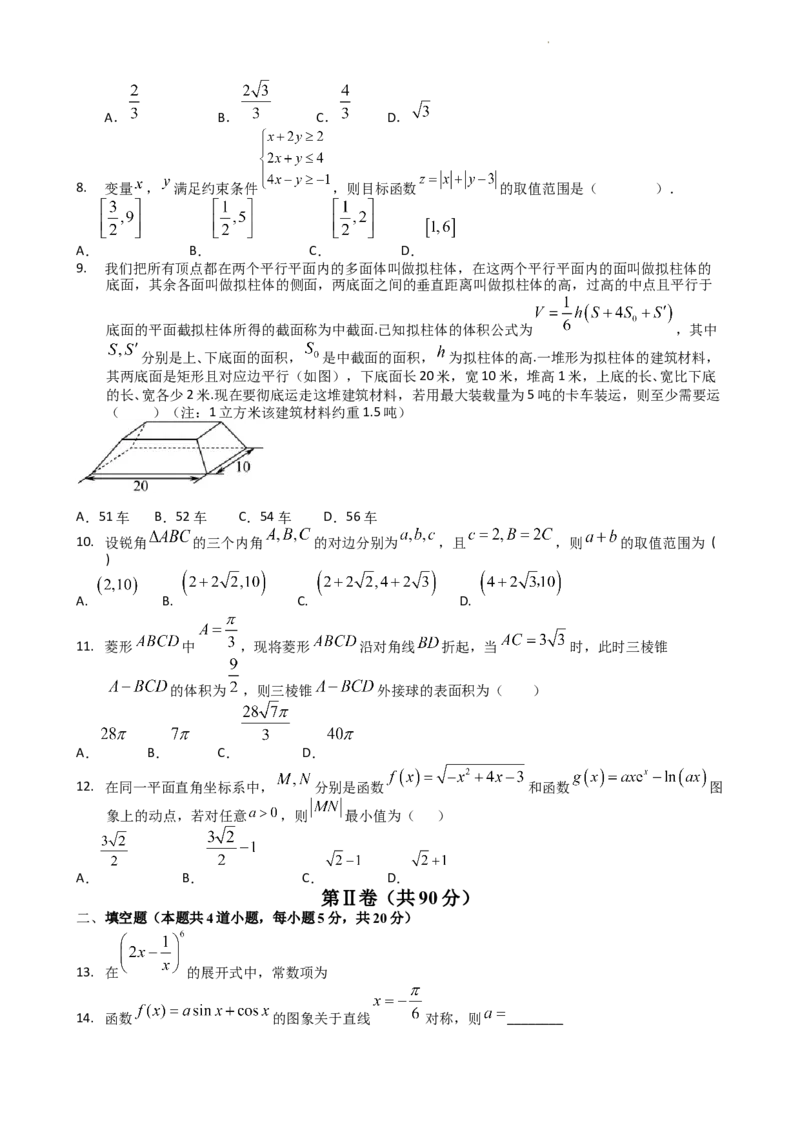
9. 我们把所有顶点都在两个平行平面内的多面体叫做拟柱体,在这两个平行平面内的面叫做拟柱体的
底面,其余各面叫做拟柱体的侧面,两底面之间的垂直距离叫做拟柱体的高,过高的中点且平行于
底面的平面截拟柱体所得的截面称为中截面.已知拟柱体的体积公式为 ,其中
分别是上、下底面的面积, 是中截面的面积, 为拟柱体的高.一堆形为拟柱体的建筑材料,
其两底面是矩形且对应边平行(如图),下底面长20米,宽10米,堆高1米,上底的长、宽比下底
的长、宽各少2米.现在要彻底运走这堆建筑材料,若用最大装载量为5吨的卡车装运,则至少需要运
( )(注:1立方米该建筑材料约重1.5吨)
A.51车 B.52车 C.54车 D.56车
10. 设锐角 的三个内角 的对边分别为 ,且 ,则 的取值范围为 (
)
A. B. C. D.
11. 菱形 中 ,现将菱形 沿对角线 折起,当 时,此时三棱锥
的体积为 ,则三棱锥 外接球的表面积为( )
A. B. C. D.
12. 在同一平面直角坐标系中, 分别是函数 和函数 图
象上的动点,若对任意 ,则 最小值为( )
A. B. C. D.
第Ⅱ卷(共90分)
二、填空题(本题共4道小题,每小题5分,共20分)
13. 在 的展开式中,常数项为
14. 函数 的图象关于直线 对称,则 ________
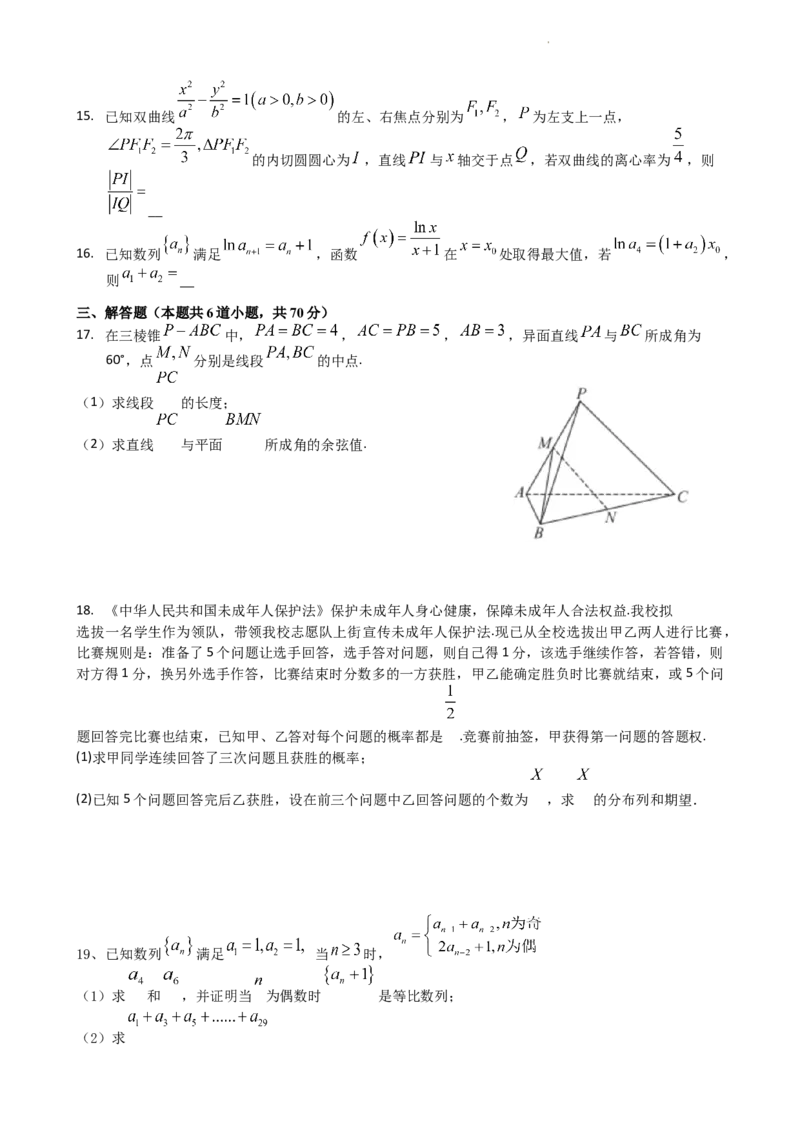
学科网(北京)股份有限公司15. 已知双曲线 的左、右焦点分别为 , 为左支上一点,
的内切圆圆心为 ,直线 与 轴交于点 ,若双曲线的离心率为 ,则
16. 已知数列 满足 ,函数 在 处取得最大值,若 ,
则
三、解答题(本题共6道小题,共70分)
17. 在三棱锥 中, , , ,异面直线 与 所成角为
60°,点 分别是线段 的中点.
(1)求线段 的长度;
(2)求直线 与平面 所成角的余弦值.
18. 《中华人民共和国未成年人保护法》保护未成年人身心健康,保障未成年人合法权益.我校拟
选拔一名学生作为领队,带领我校志愿队上街宣传未成年人保护法.现已从全校选拔出甲乙两人进行比赛,
比赛规则是:准备了5个问题让选手回答,选手答对问题,则自己得1分,该选手继续作答,若答错,则
对方得1分,换另外选手作答,比赛结束时分数多的一方获胜,甲乙能确定胜负时比赛就结束,或5个问
题回答完比赛也结束,已知甲、乙答对每个问题的概率都是 .竞赛前抽签,甲获得第一问题的答题权.
(1)求甲同学连续回答了三次问题且获胜的概率;
(2)已知5个问题回答完后乙获胜,设在前三个问题中乙回答问题的个数为 ,求 的分布列和期望.
19、已知数列 满足 当 时,
(1)求 和 ,并证明当 为偶数时 是等比数列;
(2)求
学科网(北京)股份有限公司20、已知抛物线 的焦点为 ,过点 作抛物线 的两条切线,切点分别为
, .
(1)求抛物线 的方程;
(2)过点 作两条倾斜角互补的直线 , 交抛物线 于 两点, 交抛物线 于 两点,连
接 ,设 的斜率分别为 ,求 的值;
(3)设 ,求 的值.
21、设
(1)当 ,求函数 的零点个数.
(2)函数 ,若对任意 ,恒有 ,求实数 的取值范围
选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.
[选修4-4:坐标系与参数方程](10分)
22、在直角坐标系xOy中,曲线 的渐近线方程为 , ,直线 过点
,且倾斜角为 .以点 为极点,以从点 出发与x轴正方向同方向的射线为极轴,建立极
坐标系,点 在曲线 上.
(1)写出曲线 在第二象限的参数方程和直线 的极坐标方程;
(2)曲线 与直线 相交于点 ,线段 的中点为 ,求 的面积.
[选修4-5:不等式选讲](10分)
23、设 ,
学科网(北京)股份有限公司(1)解不等式:
(2)设 的最大值为 ,已知正数 和 满足 ,令 ,求 的最小
值.
学科网(北京)股份有限公司