文档内容
阿克苏市实验中学 2023—2024 学年第一学期高三年级第一次月考考试
数学试卷
考试时间:120分钟 满分:150分
一、选择题(本大题共8个小题,每小题5分,共40分,在每小题给出的四个选项中,只有一
项是符合题目要求的)
1. 已知集合 ,则集合 的子集个数为( )
A. 1 B. 2 C. 4 D. 8
【答案】C
【解析】
【分析】先化简集合A,再求得其子集即可
【详解】由已知可得 ,其子集为 ,子集个数为4个
故选:C.
2. “ ”是“ ”的( )条件
A. 充分不必要 B. 必要不充分
C. 充分必要 D. 既不充分也不必要
【答案】B
【解析】
的
【分析】根据充分性和必要性 概念直接求解即可.
【详解】因为 , ,
所以“ ”是“ ”的必要不充分条件,
故选:B
3. 不等式 的解集为( )
A. B.
C. ,或 D. ,或
【答案】B
第1页/共16页
学科网(北京)股份有限公司【解析】
【分析】对于二次项系数是负数的一元二次不等式,可以先把二次项系数化成正数,再求解.
【详解】不等式可化为 ,解得 .
故选:B.
4. 若 , , ,则有( )
A. B. C. D.
【答案】B
【解析】
【分析】由指数和对数函数的性质,利用中间值确定a,b,c的范围,即可求解.
【详解】指数函数 在R上为减函数,则 ,即 ,
对数函数 在 上为增函数,则 ,
对数函数 在 上为增函数,则 .因此 .
故选:B.
5. 已知正数 满足 ,则 的最小值是( )
A. 17 B. 16 C. 15 D. 14
【答案】A
【解析】
【分析】先配凑 ,然后运用基本不等式求出最小值
【详解】 ,
当且仅当 ,即 , 时, 取得最小值 .
故选: .
第2页/共16页
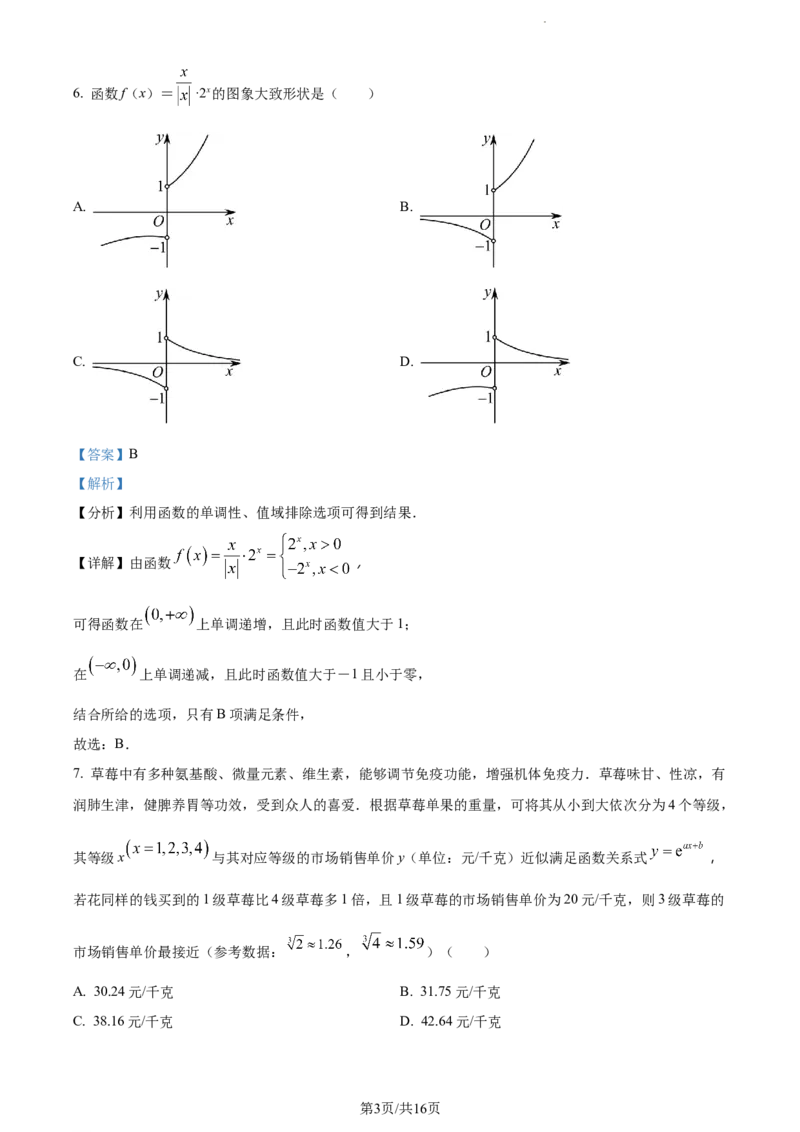
学科网(北京)股份有限公司6. 函数f(x)= ·2x的图象大致形状是( )
A. B.
C. D.
【答案】B
【解析】
【分析】利用函数的单调性、值域排除选项可得到结果.
【详解】由函数 ,
可得函数在 上单调递增,且此时函数值大于1;
在 上单调递减,且此时函数值大于-1且小于零,
结合所给的选项,只有B项满足条件,
故选:B.
7. 草莓中有多种氨基酸、微量元素、维生素,能够调节免疫功能,增强机体免疫力.草莓味甘、性凉,有
润肺生津,健脾养胃等功效,受到众人的喜爱.根据草莓单果的重量,可将其从小到大依次分为4个等级,
其等级x 与其对应等级的市场销售单价y(单位:元/千克)近似满足函数关系式 ,
若花同样的钱买到的1级草莓比4级草莓多1倍,且1级草莓的市场销售单价为20元/千克,则3级草莓的
市场销售单价最接近(参考数据: , )( )
A. 30.24元/千克 B. 31.75元/千克
C. 38.16元/千克 D. 42.64元/千克
第3页/共16页
学科网(北京)股份有限公司【答案】B
【解析】
【分析】根据题意,由指数的运算性质,代入计算,即可得到结果.
【详解】由题意可知, ,解得 ,由 ,
可得 ,
故选:B.
8. 已知 ,若 ,则 所在区间为( )
A. B.
C. D.
【答案】B
【解析】
【分析】利用零点存在性定理求解即可.
【详解】由已知得函数 连续且单调递增,
因为 , ,
所以 ,
由零点存在性定理可知存在 使得 ,
故选: .
二、选择题(本大题共4个小题,每小题5分,共20分,在每小题给出的四个选项中,有多项
符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
9. 已知集合 ,则下列式子表示正确的是( )
A. B. C. D.
第4页/共16页
学科网(北京)股份有限公司【答案】ACD
【解析】
【分析】先求得集合 ,然后根据元素与集合的关系,集合与集合的关系求得正确答案.
【详解】由题意可知, ,所以 , , .,ACD选项正确.
是
B选项, 集合,不是元素,所以不能用“ ”,B选项错误.
故选:ACD
10. 若幂函数 的图像经过点 ,则下列命题中,正确的有( )
A. 函数 为奇函数 B. 函数 为偶函数
C. 函数 在 为减函数 D. 函数 在 为增函数
【答案】AC
【解析】
【分析】先根据幂函数图像经过点 ,求出函数解析式,然后利用幂函数的基本性质即可求解.
【详解】因为 是幂函数,所以设 ,
又 的图像经过点 ,所以 ,所以 ,即 ,
所以函数 为奇函数,且在 为减函数,故AC正确,BD错误;
故选:AC.
11. 已知函数 ,则下列结论中正确的是( )
A. 函数 有且仅有一个零点0 B.
C. 在 上单调递增 D. 在 上单调递减
【答案】BC
【解析】
【分析】根据分段函数解析式,结合对数函数性质判断单调性和零点.
第5页/共16页
学科网(北京)股份有限公司【详解】由函数 ,可得 有两个零点0、1,故A错误;
由于 ,故B正确;
当 时 ,所以 在 上单调递增,故C正确;
当 时 ,所以 在 上单调递减, 上单调递增,故D错误.
故选:BC.
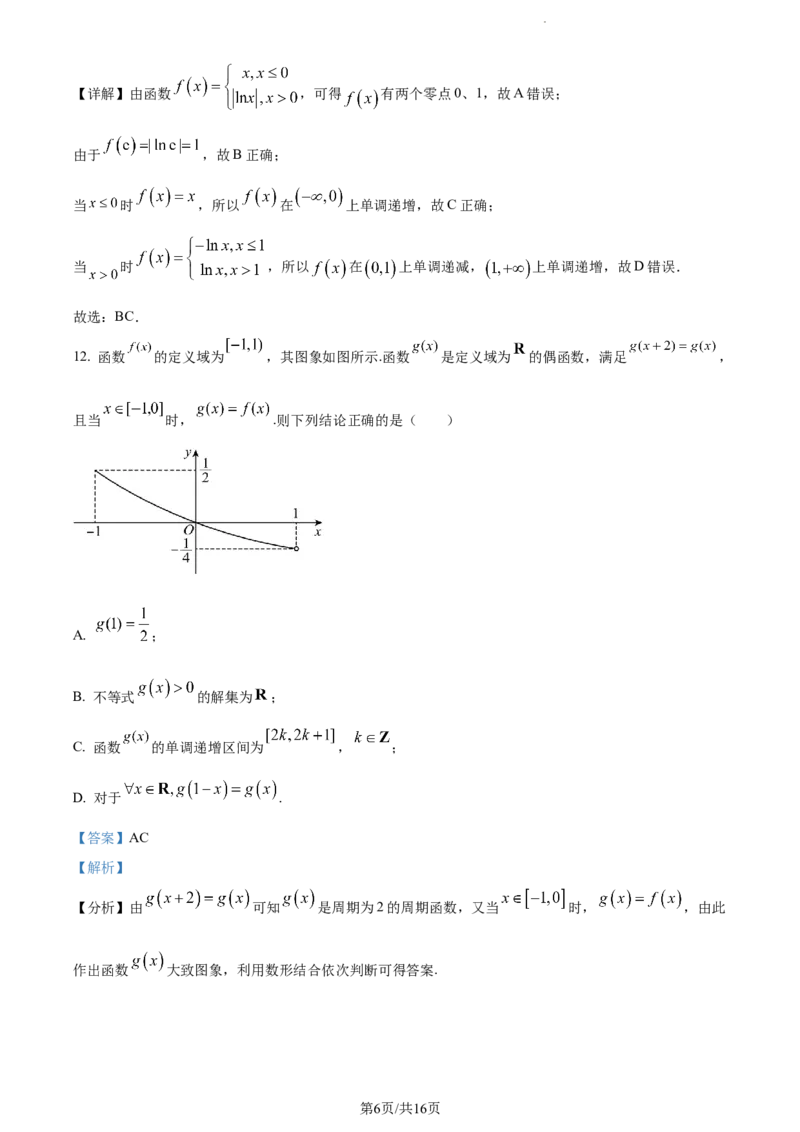
12. 函数 的定义域为 ,其图象如图所示.函数 是定义域为 的偶函数,满足 ,
且当 时, .则下列结论正确的是( )
A. ;
B. 不等式 的解集为 ;
C. 函数 的单调递增区间为 , ;
D. 对于 .
【答案】AC
【解析】
【分析】由 可知 是周期为2的周期函数,又当 时, ,由此
作出函数 大致图象,利用数形结合依次判断可得答案.
第6页/共16页
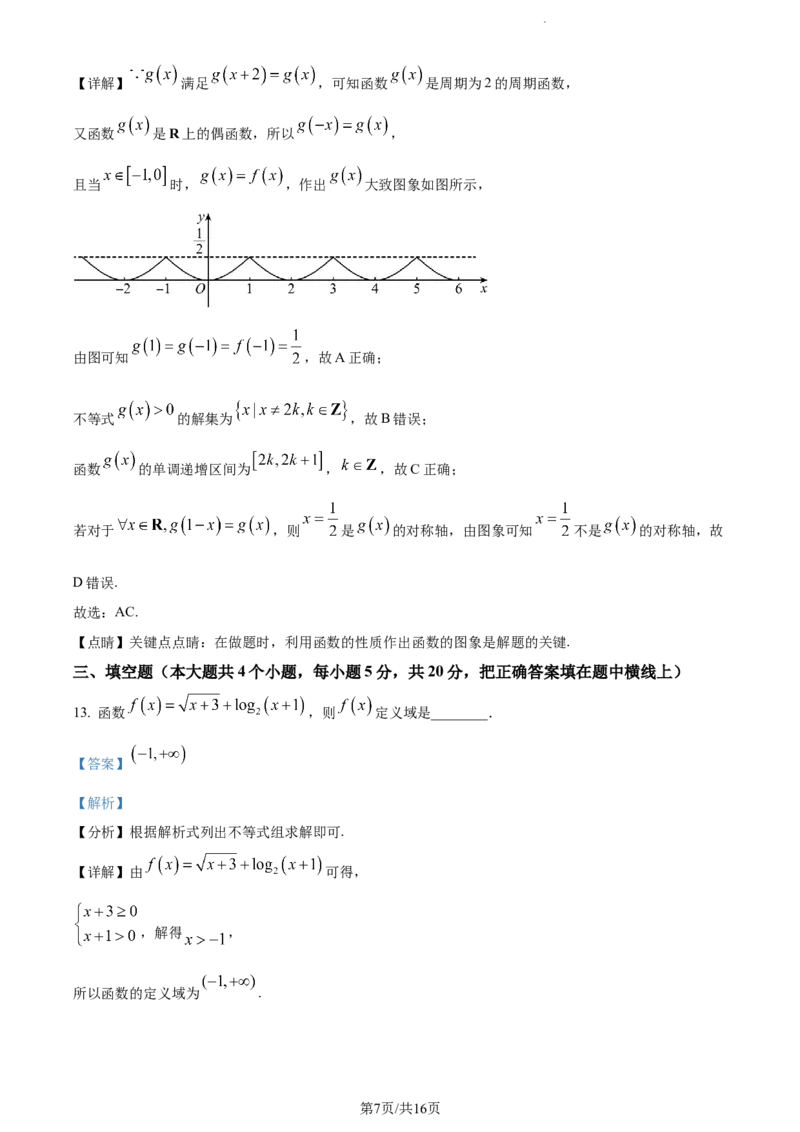
学科网(北京)股份有限公司【详解】 满足 ,可知函数 是周期为2的周期函数,
又函数 是R上的偶函数,所以 ,
且当 时, ,作出 大致图象如图所示,
由图可知 ,故A正确;
不等式 的解集为 ,故B错误;
函数 的单调递增区间为 , ,故C正确;
若对于 ,则 是 的对称轴,由图象可知 不是 的对称轴,故
D错误.
故选:AC.
【点睛】关键点点睛:在做题时,利用函数的性质作出函数的图象是解题的关键.
三、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
13. 函数 ,则 定义域是________.
【答案】
【解析】
【分析】根据解析式列出不等式组求解即可.
【详解】由 可得,
,解得 ,
所以函数的定义域为 .
第7页/共16页
学科网(北京)股份有限公司故答案为: .
14. 函数 的零点个数为_________.
【答案】
【解析】
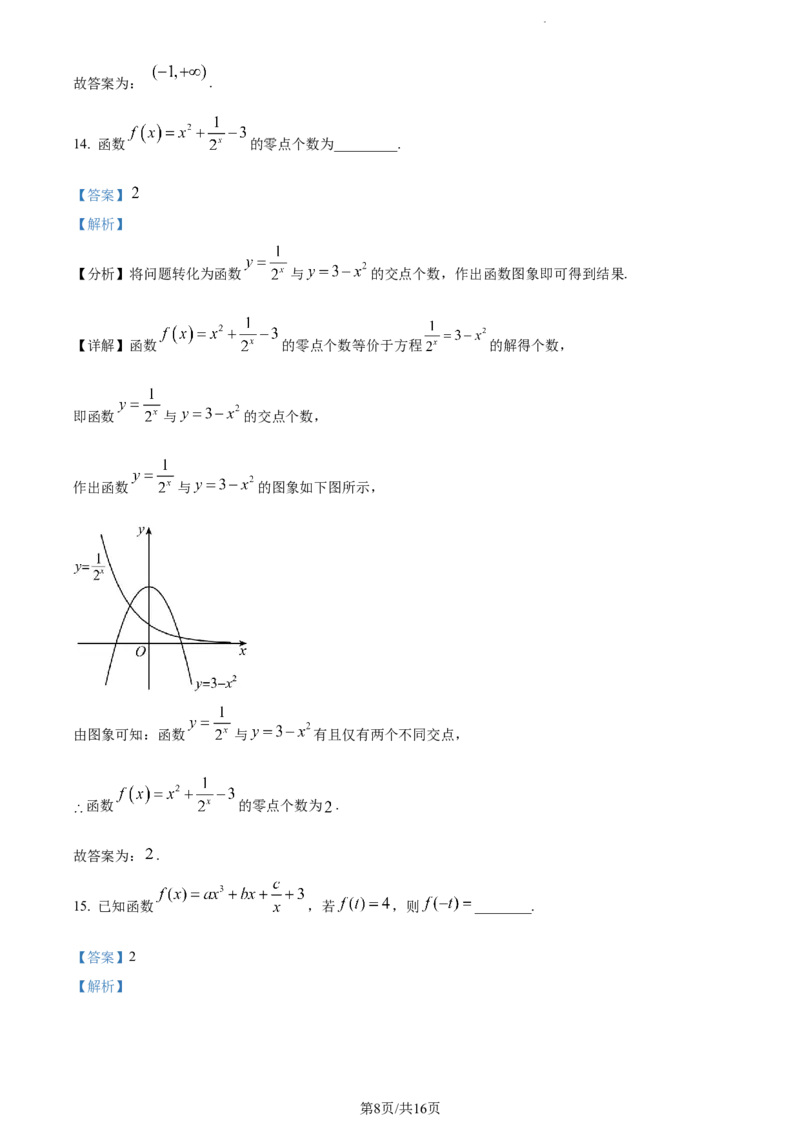
【分析】将问题转化为函数 与 的交点个数,作出函数图象即可得到结果.
【详解】函数 的零点个数等价于方程 的解得个数,
即函数 与 的交点个数,
作出函数 与 的图象如下图所示,
由图象可知:函数 与 有且仅有两个不同交点,
函数 的零点个数为 .
故答案为: .
15. 已知函数 ,若 ,则 ________.
【答案】2
【解析】
第8页/共16页
学科网(北京)股份有限公司【分析】得出 即可
【详解】因为
所以
即 ,因为 ,所以
故答案为:2
【点睛】若 是奇函数,则 的图象关于 对称,满足 .
16. 已知函数 ,则 __________.
【答案】
【解析】
【分析】根据解析式可推导得到 ,进而求得结果.
【详解】 , .
故答案为: .
四、解答题(本大题共6个大题,共70分,解答应写出文字说明,证明过程或演算步骤)
17. 已知函数 ,且 .
(1)求 的值;
的
(2)判定 奇偶性.
【答案】(1)1 (2)奇函数
【解析】
【分析】(1)根据 ,待定系数即可求得参数值;
(2)根据函数奇偶性的定义,结合函数定义域,即可容易判断.
【小问1详解】
第9页/共16页
学科网(北京)股份有限公司,
.
【小问2详解】
由(1)得: ,
则 定义域为 ,
,
为定义在 上的奇函数.
18. 已知奇函数
(1)求 的值;
(2)若函数 在区间 上单调递增,试确定a的取值范围.
【答案】(1)0; (2) .
【解析】
【分析】(1)先根据函数的奇偶性确定 的值,再求函数值即可;
(2)先画出函数的图像,结合图像找到函数的单调递增区间,依题意得到 的范围,解不等式即得.
【小问1详解】
当 时, ,因为 是奇函数,
所以 ,
所以 .故 .
【小问2详解】
第10页/共16页
学科网(北京)股份有限公司依题意作出函数 图像如图,
的
因函数 在区间 上单调递增,故 ,
则有 ,解得 或 .
即实数a的取值范围为 .
19. 已知函数 且 ,且 的图象过点 .
(1)求 的解析式;
(2)若 ,求实数 的取值范围.
【答案】(1)
(2)
【解析】
【分析】(1)由 ,求得 ,从而可得答案;
(2)根据 在R上单调递增,可得 ,进而可得答案.
【小问1详解】
的图象过点 ,
,
第11页/共16页
学科网(北京)股份有限公司又
【小问2详解】
在R上单调递增
.
20. 已知函数 .
(1)求函数 恒过哪一个定点,写出该点坐标;
(2)令函数 ,当 时,证明:函数 在区间 上有零点.
【答案】(1)恒过定点 ,坐标
(2)证明见解析
【解析】
【分析】(1)根据题意,可得函数 的解析式,再由对数函数过定点,代入计算,即可得到结果;
(2)根据题意,由条件可得函数 的解析式,再由零点存在定理判断即可.
【小问1详解】
由题意知函数 ,故 ,
令 ,
即函数 恒过定点 ,该点坐标为 ;
【小问2详解】
第12页/共16页
学科网(北京)股份有限公司证明:由题意 ,
当 时, ,
即 ,
则 ,又 ,
故函数 在区间 上有零点.
21. 定义在 上的偶函数 ,当 时, .
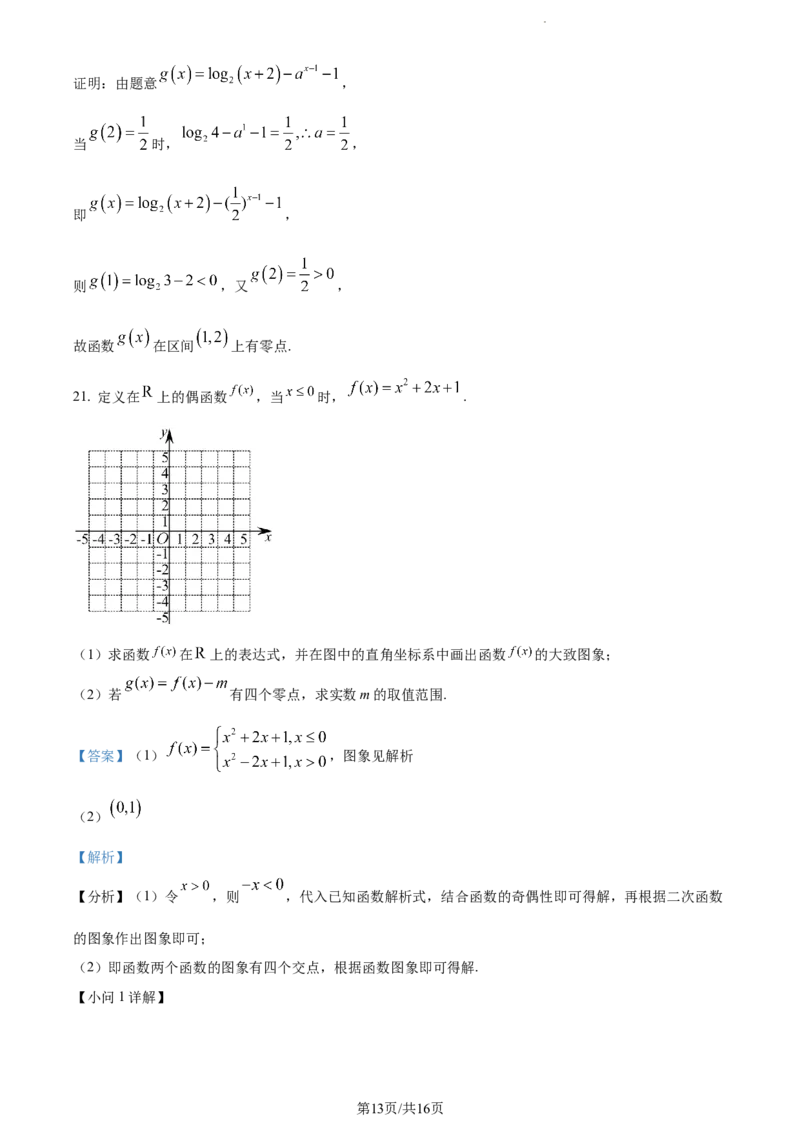
(1)求函数 在 上的表达式,并在图中的直角坐标系中画出函数 的大致图象;
(2)若 有四个零点,求实数m的取值范围.
【答案】(1) ,图象见解析
(2)
【解析】
【分析】(1)令 ,则 ,代入已知函数解析式,结合函数的奇偶性即可得解,再根据二次函数
的图象作出图象即可;
(2)即函数两个函数的图象有四个交点,根据函数图象即可得解.
【小问1详解】
第13页/共16页
学科网(北京)股份有限公司因为定义在 上的偶函数 ,当 时, ,
则 ,
令 ,则 ,
则 ,
所以 ,
作出函数图象,如图所示:
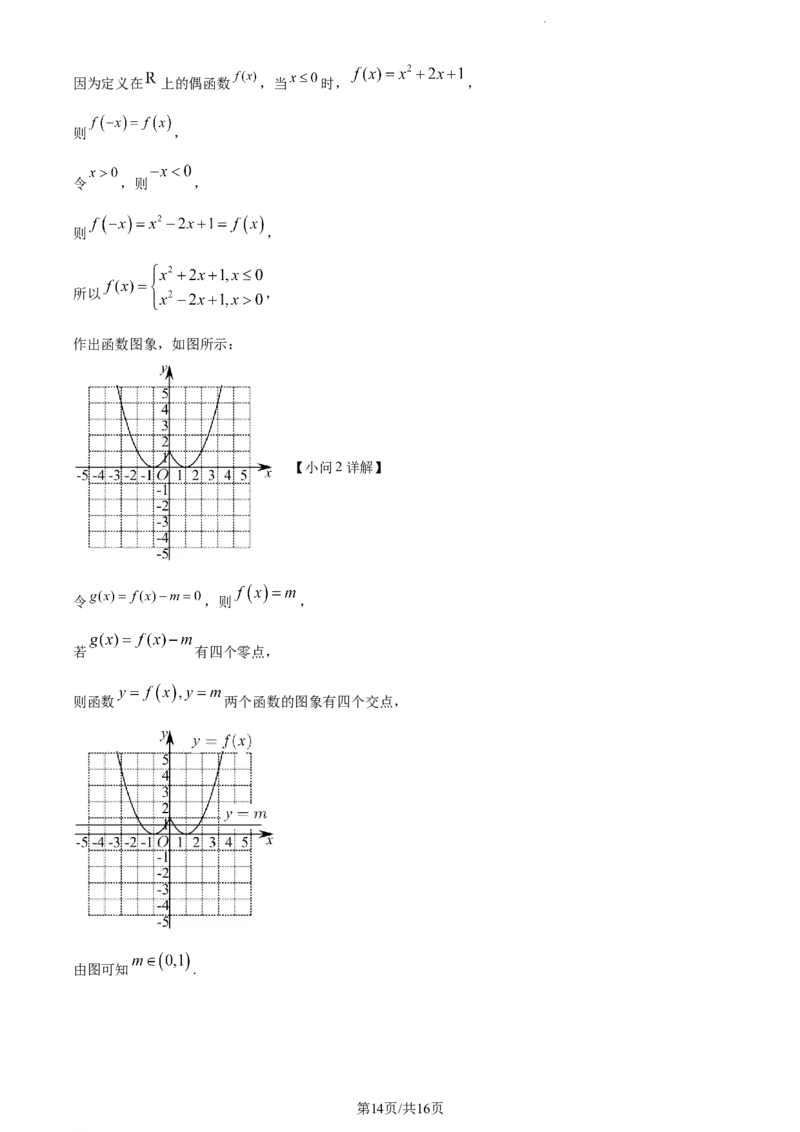
【小问2详解】
令 ,则 ,
若 有四个零点,
则函数 两个函数的图象有四个交点,
由图可知 .
第14页/共16页
学科网(北京)股份有限公司22. 已知二次函数 ,且不等式 的解集为 .
(1)求 解析式;
(2)若不等式 在 上有解,求实数 的取值范围.
【答案】(1)
(2)
【解析】
【分析】(1)根据一元二次不等式的解集结合韦达定理求得 ,即得答案.
(2)不等式 在 上有解,即 在 上的最大值,采用换
元法结合基本不等式求得 的最大值,即得答案.
【小问1详解】
由题意知 的解集为 ,
故方程 的两个根是1和3,
故 ,即 ,
故 .
【小问2详解】
由题意 在 上有解,即 在 上有解,
∵ ,∴ 在 上的最大值,
第15页/共16页
学科网(北京)股份有限公司设 ,则 ,则
又 ,当且仅当 即 时,等号成立,
∴ ,即实数 的取值范围为 .
第16页/共16页
学科网(北京)股份有限公司