文档内容
邕衡金卷·名校联盟
柳州高中、南宁三中2024届一轮复习诊断性联考
数 学
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需
改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在
本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
1.已知集合A={1,3,4},集合B={2,3,4,6},则如图中的阴影部分表示( )
A. {3,4}
B.{1}
C.{2,6}
D.{1,2,3,4,6}
2.已知命题p:∃ x∈R,lgx+x≥3,则 ¬ p为( )
A.∀x∈R,lgx+x<3 B.∃x∈R,lgx+x<3
C.∀x∈R,lgx+x≥3 D.∃x∈R,lgx+x≤3
3.一组数据从小到大的顺序排列如下:9,10,12,15,17,18,22,26,经计算,则 75%分位数是
( )
A. 18 B.20 C.21 D.22
π 3
4.若cos α+ = ,则sin2α=( )
4 5
7 7 9 9
A. B.− C. D.−
25 25 25 25
5.已知 f
(
x
)= cosx
为奇函数,则a =( )
(x2 +3x)(x+a)
A.3 B.− 3 C.0 D.− 1
数学试题 第 1 页(共 4 页)6.抛物线有如下光学性质:平行于抛物线对称轴的光线,经过抛物线上的一点反射后,反射
光线经过抛物线的焦点.过点P(2 2,5)且平行于y 轴的一条光线射向抛物线C:x2 = 4y 上
的A点,经过反射后的反射光线与C相交于点B,则|AB|=( )
7 9
A. B.9 C.36 D.
2 2
7.如果一个数列从第 2 项起,每一项与它前一项的和除以与它前一项的差等于同一个常数,
那么这个数列就叫做“和差等比数列”.已知{a }是“和差等比数列”,a =1,a =3,则
n 1 2
满足使不等式a >100的n的最小值是( )
n
A. 8 B.7 C.6 D.5
8.某同学参加学校组织的数学知识竞赛,在 5 道四选一的单选题中有 3 道有思路,有 2 道完
1
全没有思路,有思路的题目每道做对的概率为 ,没有思路的题目只好任意猜一个答
2
案.若从这5道题目中任选2题,则该同学2道题目都做对的概率为( )
1 7 3 5
A. B. C. D.
4 32 16 32
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.若复数z满足zi=1−i,则下列命题正确的有( )
A. z的虚部是−1 B.|z| = 2
C.z2 = 2 D.z是方程x2+2x+2=0的一个根
10.在物理学中,把物体受到的力(总是指向平衡位置)正比于它离开平衡位置的距离的运动
称为“简谐运动”.在适当的直角坐标系下,某个简谐运动可以用函数
f ( x )= Asin (ωx+ϕ)( A>0,ω>0,ϕ<π ) 的部分图象如图所示,则下列结论正确的是
( )
1 π
A. ω=2,频率为 ,初相为
π 6
π
B.函数 f ( x ) 的图象关于直线x=− 对称
6
( )
π 13π
C.函数 f x 在 , 上的值域为[0,2]
12 24
( )
D.若把 f x 图像上所有点的横坐标缩短为原
2 π π
来的 倍,纵坐标不变,再向左平移 个单位,则所得函数是y=2sin3x+
3 12 12
数学试题 第 2 页(共 4 页)
11.在边长为 2 的正方体 ABCD−ABC D 中,动点 M 满足 AM =xAB+ yAD+zAA ,
1 1 1 1 1
(x,y,z∈R且x≥0,y≥0,z≥0),下列说法正确的是( )
A. 当x= 1 ,z=0,y∈[ 0,1 ] 时,BM +MD的最小值为 13
4 1
1 10
B.当x= y=1,z= 时,异面直线BM与CD 所成角的余弦值为
1
2 5
2 5 4 2π
C.当x+ y+z=1,且AM = 时,则M的轨迹长度为
3 3
6
D.当x+ y=1,z=0时,AM与平面AB D 所成角的正弦值的最大值为
1 1
3
三、填空题:本题共3小题,每小题5分,共15分.
( ) ( )
12.已知向量a=( 1,m ) ,b=( 3,−1 ) .若 2a−b // a+2b ,则实数m的值为 .
1 1
13.已知(ax+ )5(2x− )(a为常数)的展开式中所有项的系数和为32,则展开式中x2的系数
x x
为 (用数字作答).
14.已知数列 1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是 20,接下
来的两项是20,21,再接下来的三项是20,21,22,依此类推,若该数列的前n项和为S ,
n
若 log (S )∈Z,n∈N*,则称(n,log (S ))为“好数对”,如 log (S )=log 20=0,
2 n 2 n 2 1 2
log (S )=log 21=1,则(1,0),(2,1)都是“好数对”,当n≥66时,第一次出现的“好数对”
2 2 2
是 .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
a−b sinA−sinC
15.(13分)记△ABC的内角A,B,C的对边分别为a,b,c,已知 = .
c sinA+sinB
(1)求角B的大小;
(2)若b =2,求△ABC周长的最大值.
16.(15 分)某校为了丰富学生课余生活,体育节组织定点投篮比赛.为了解学生喜欢篮球是否
与性别有关,随机抽取了男、女同学各100名进行调查,部分数据如表所示:
喜欢篮球 不喜欢篮球 合计
男生 40
女生 30
合计
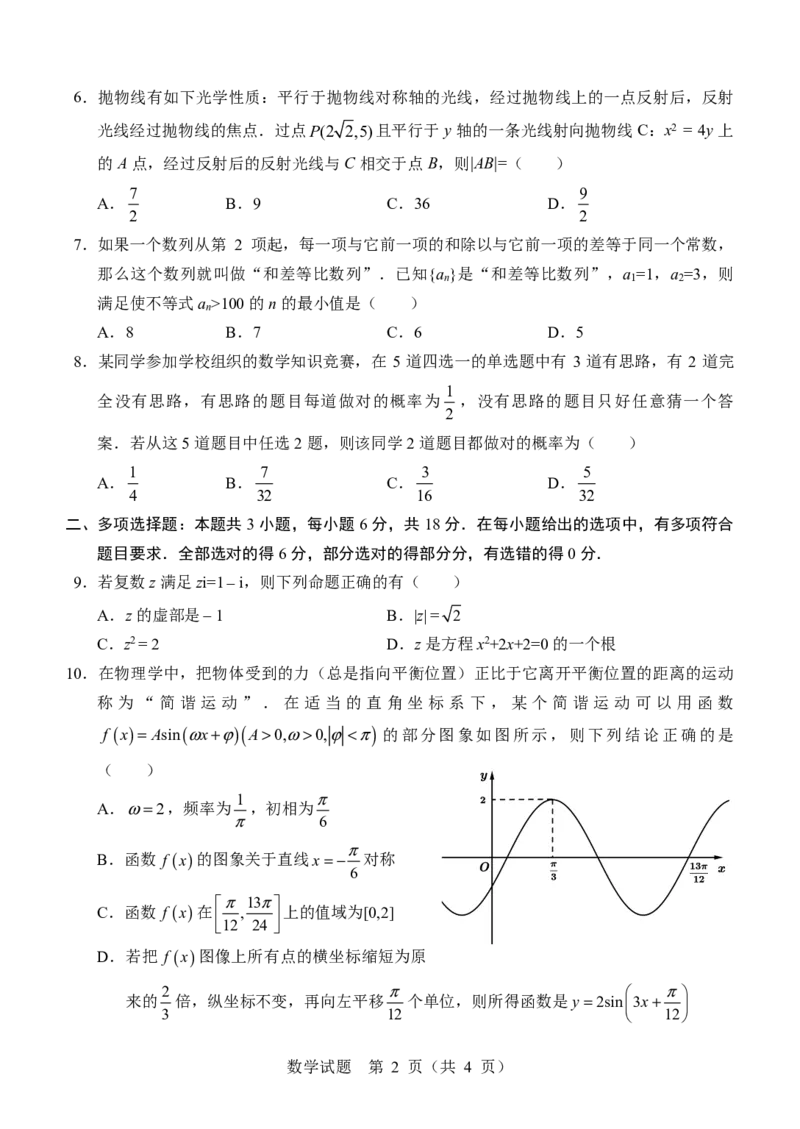
数学试题 第 3 页(共 4 页)(1)根据所给数据完成上表,依据小概率值α=0.001的χ2独立性检验,能否据此推断该校
学生喜欢篮球与性别有关?
(2)篮球指导老师从喜欢篮球的学生中抽取了2名男生和1名女生进行投篮示范.已知这两
3 2
名男生投进的概率均为 ,这名女生投进的概率为 ,每人投篮一次,假设各人投篮
4 3
相互独立,求3人投进总次数X的分布列和数学期望.
n(ad −bc)2
附:χ2 =
(a+b)(c+d)(a+c)(b+d)
α 0.1 0.05 0.01 0.005 0.001
x 2.706 3.841 6.635 7.879 10.828
α
17.(15分)在如图所示的五面体ABCDEF中,ABEF共面,△ADF是正三角形,四边形ABCD
2π
为菱形,∠ABC= ,EF∥平面ABCD,AB=2EF=2,点M为BC中点.
3
(1)证明:EM∥平面BDF;
(2)已知EM=2,求平面BDF与平面BEC所成二面角的正弦值.
18.(17分)已知函数 f(x)=lnx−ax+a,g(x)=(x−1)ex−a −ax+1(a∈R).
( )
(1)若 f x ≤0,求a的值;
(2)当a∈(
0,1
]
时,证明:g
(
x
)
≥ f
(
x
)
.
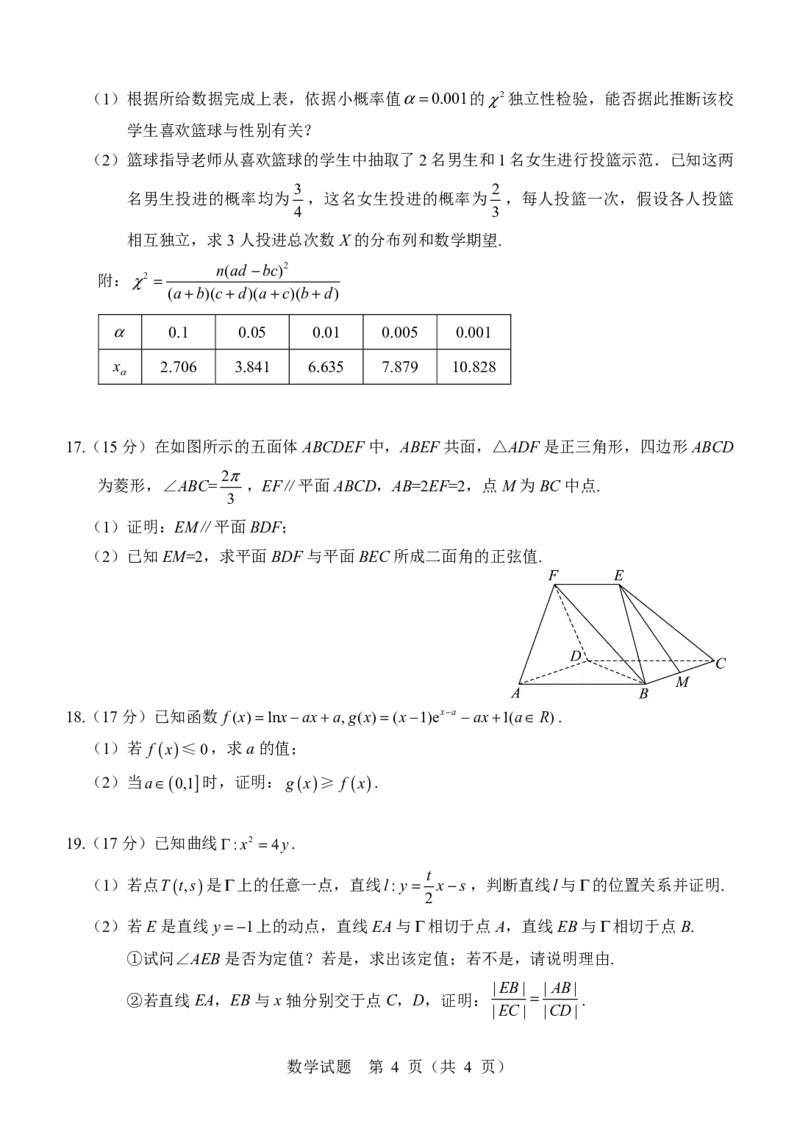
19.(17分)已知曲线Γ:x2 =4y.
(1)若点T ( t,s ) 是Γ上的任意一点,直线l:y= t x−s,判断直线l与Γ的位置关系并证明.
2
(2)若E是直线y=−1上的动点,直线EA与Γ相切于点A,直线EB与Γ相切于点B.
①试问∠AEB是否为定值?若是,求出该定值;若不是,请说明理由.
|EB| |AB|
=
②若直线EA,EB与x轴分别交于点C,D,证明: .
|EC| |CD|
数学试题 第 4 页(共 4 页)