吉林省通化市梅河口市第五中学2025-2026学年高二上学期10月月考试题数学Word版含解析_2025年10月高二试卷_251016吉林省通化市梅河口市第五中学2025-2026学年高二上学期10月月考试题(全）

高二数学
一、单选题：本题共 8 小题，每小题 5 分，共 40 分．在每小题给出的四个选项中，只有一项是符合题目要
求的.
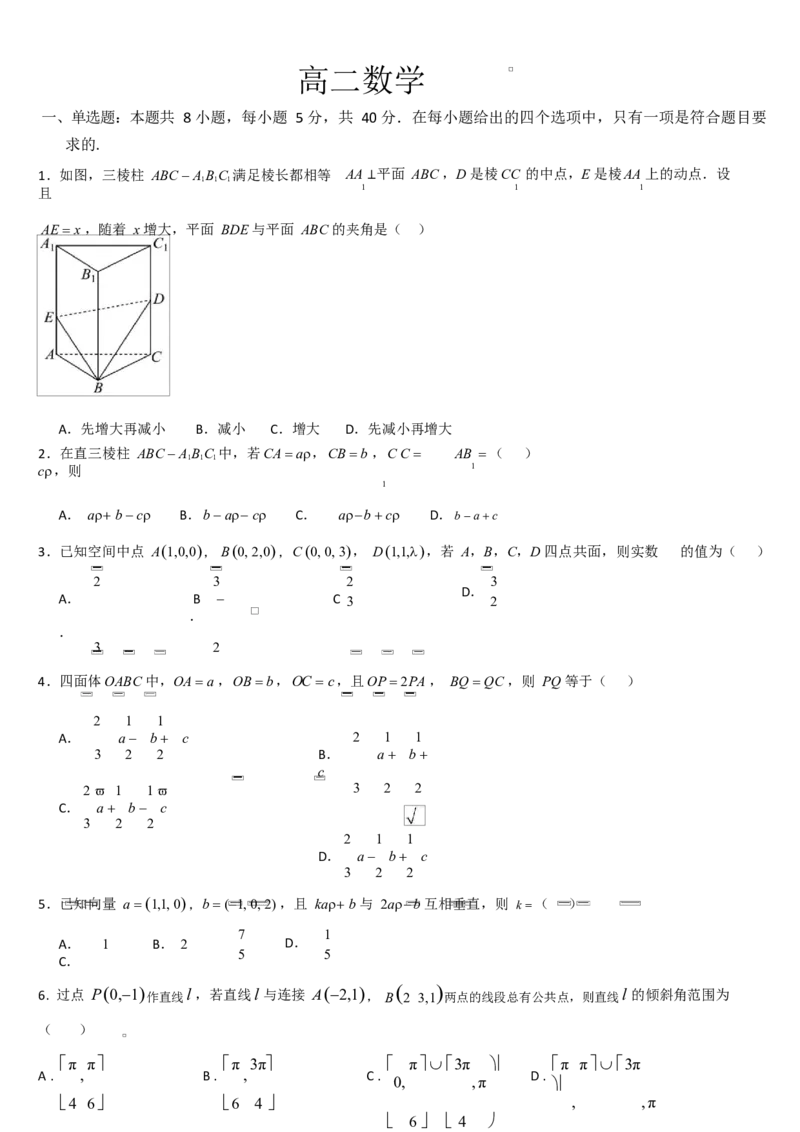
1．如图，三棱柱 ABC  A BC 满足棱长都相等 AA 平面 ABC ，D 是棱CC 的中点，E 是棱AA 上的动点．设
1 1 1
且 1 1 1
⊥
AE  x ，随着 x 增大，平面 BDE 与平面 ABC 的夹角是（ ）
A．先增大再减小 B．减小 C．增大 D．先减小再增大
2．在直三棱柱 ABC  A BC 中，若CA  a，CB  b ，C C  AB  （ ）
1 1 1
c，则 1
1
A． a b  c B．b  a c C． ab  c D．b  a  c
3．已知空间中点 A1,0,0， B0, 2,0，C 0, 0, 3， D1,1,，若 A，B，C，D 四点共面，则实数 的值为（ ）
2 3 2 3
D．
A．  B  C 3 2
．
．
3 2
4．四面体OABC 中，OA  a ，OB  b，OC  c，且OP  2PA ， BQ  QC ，则 PQ 等于（ ）
    
2 1 1 
A．  a  b  c 2 1 1
3 2 2 B．  a  b 
 c
2  1 1  3 2 2
C． a  b  c  
3 2 2 
2 1 1
D． a  b  c
3 2 2
5．已知向量 a  1,1, 0，b  (1, 0, 2) ，且 ka b 与 2ab 互相垂直，则 k  （ ）
7 1
A． 1 B． 2 D．
5 5
C． 
6. 过点 P0,1 作直线l ，若直线l 与连接 A2,1 ， B  2 3,1  两点的线段总有公共点，则直线l 的倾斜角范围为
（ ）
π π π 3π  π  3π  π π  3π
A . , B . , C . D .
0, ,π 
   
4 6 6 4     , ,π
 6   4    6 2  4 
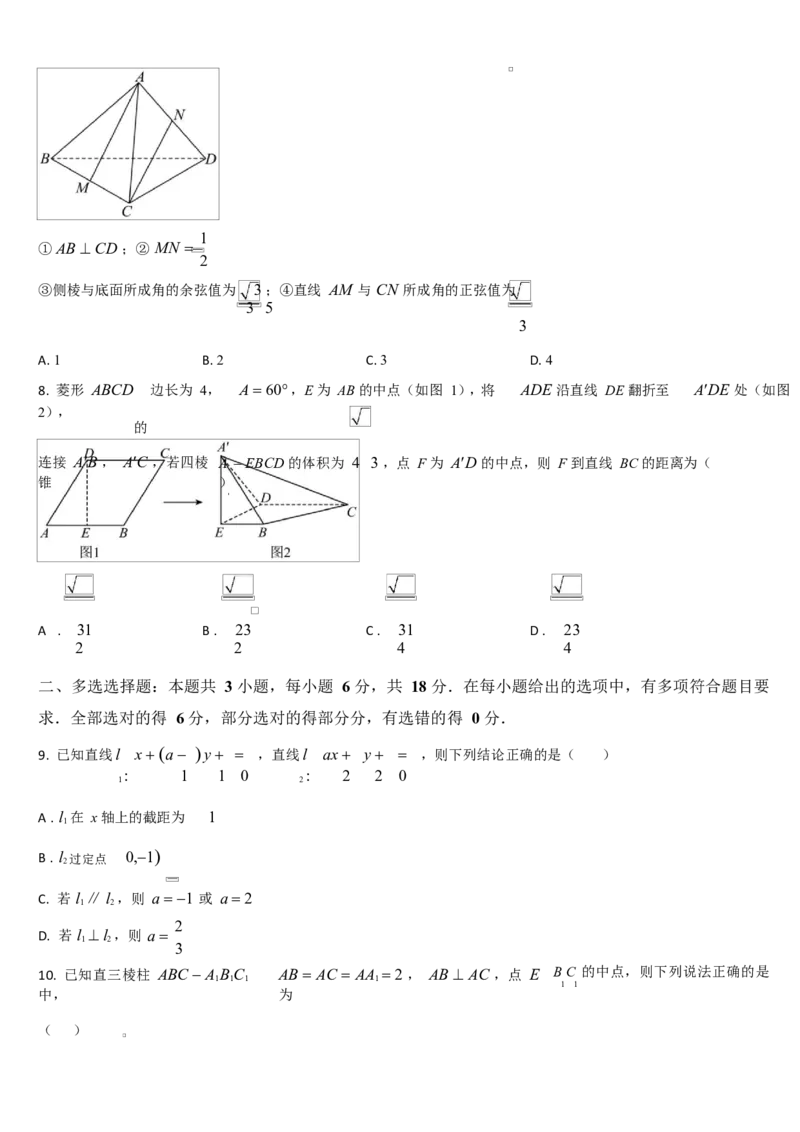
7. 如图，在棱长为1的正四面体 ABCD 中，点 M ， N 分别为棱 BC ， AD 的中点，则下列命题正确的个数为（
）1
① AB  CD ；② MN 
2
③侧棱与底面所成角的余弦值为 3；④直线 AM 与 CN 所成角的正弦值为
3 5
3
A. 1 B. 2 C. 3 D. 4
8. 菱形 ABCD 边长为 4，A  60，E 为 AB 的中点（如图 1），将 ADE 沿直线 DE 翻折至 ADE 处（如图
2），
的
连接 AB ， AC ，若四棱 A  EBCD 的体积为 4 3 ，点 F 为 AD 的中点，则 F 到直线 BC 的距离为（
锥 ）
'
A . 31 B . 23 C . 31 D . 23
2 2 4 4
二、多选选择题：本题共 3 小题，每小题 6 分，共 18 分．在每小题给出的选项中，有多项符合题目要
求．全部选对的得 6 分，部分选对的得部分分，有选错的得 0 分．
9. 已知直线l x  a  y   ，直线l ax  y   ，则下列结论正确的是（ ）
: 1 1 0 : 2 2 0
1 2
A . l 在 x 轴上的截距为 1
1
B . l 过定点 0,1
2
C. 若 l ∥ l ，则 a  1 或 a  2
1 2
2
D. 若 l  l ，则 a 
1 2
3
10. 已知直三棱柱 ABC  A BC AB  AC  AA  2 ， AB  AC ，点 E B C 的中点，则下列说法正确的是
1 1 1 1
1 1
中， 为
（ ） 
A .  
1 1
AE  AB  AC  AA
1
2 2
B . AB / / 平面 ACE
1 1
C. 异面直线 AE 与 AC 所成的角的余弦值为 3
1
12
D. 点 A 到平面 ACE 的距离为 2 5
1
5
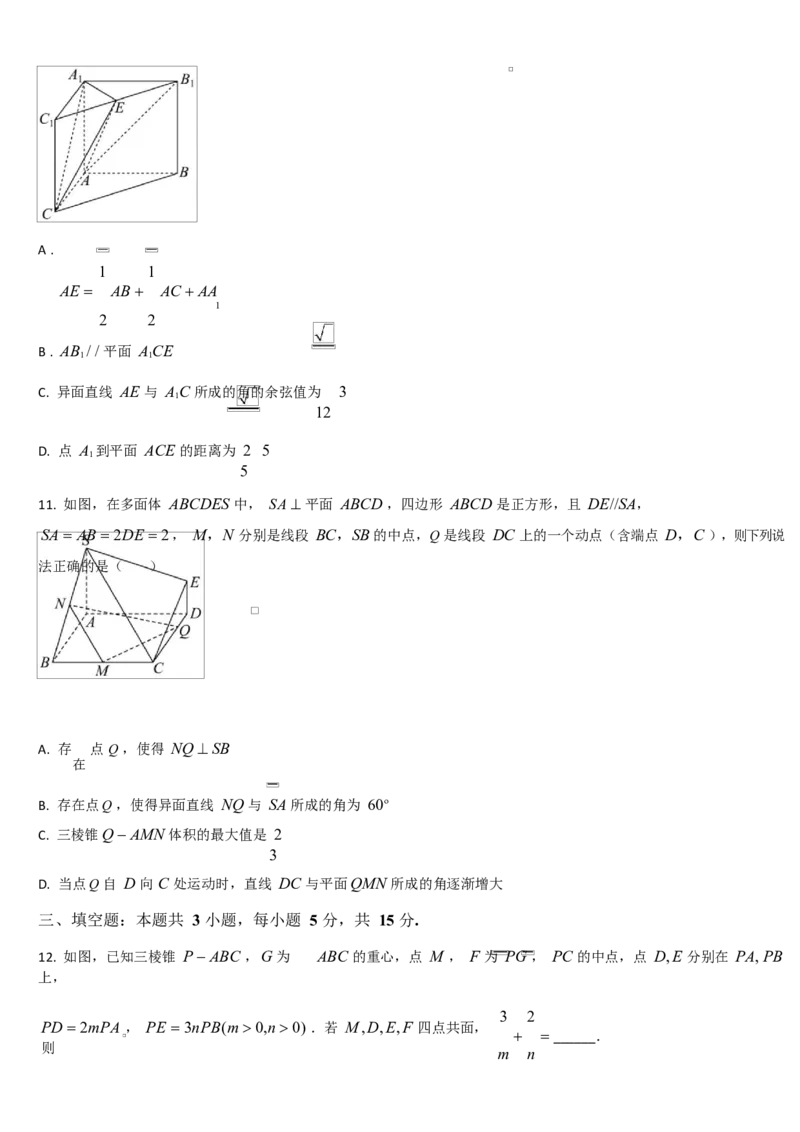
11. 如图，在多面体 ABCDES 中， SA  平面 ABCD ，四边形 ABCD 是正方形，且 DE//SA，
SA  AB  2DE  2， M，N 分别是线段 BC，SB的中点，Q 是线段 DC 上的一个动点（含端点 D，C ），则下列说
法正确的是（ ）
A. 存 点 Q ，使得 NQ  SB
在
B. 存在点Q ，使得异面直线 NQ 与 SA所成的角为 60
C. 三棱锥Q  AMN 体积的最大值是 2
3
D. 当点Q 自 D 向 C 处运动时，直线 DC 与平面QMN 所成的角逐渐增大
三、填空题：本题共 3 小题，每小题 5 分，共 15 分.
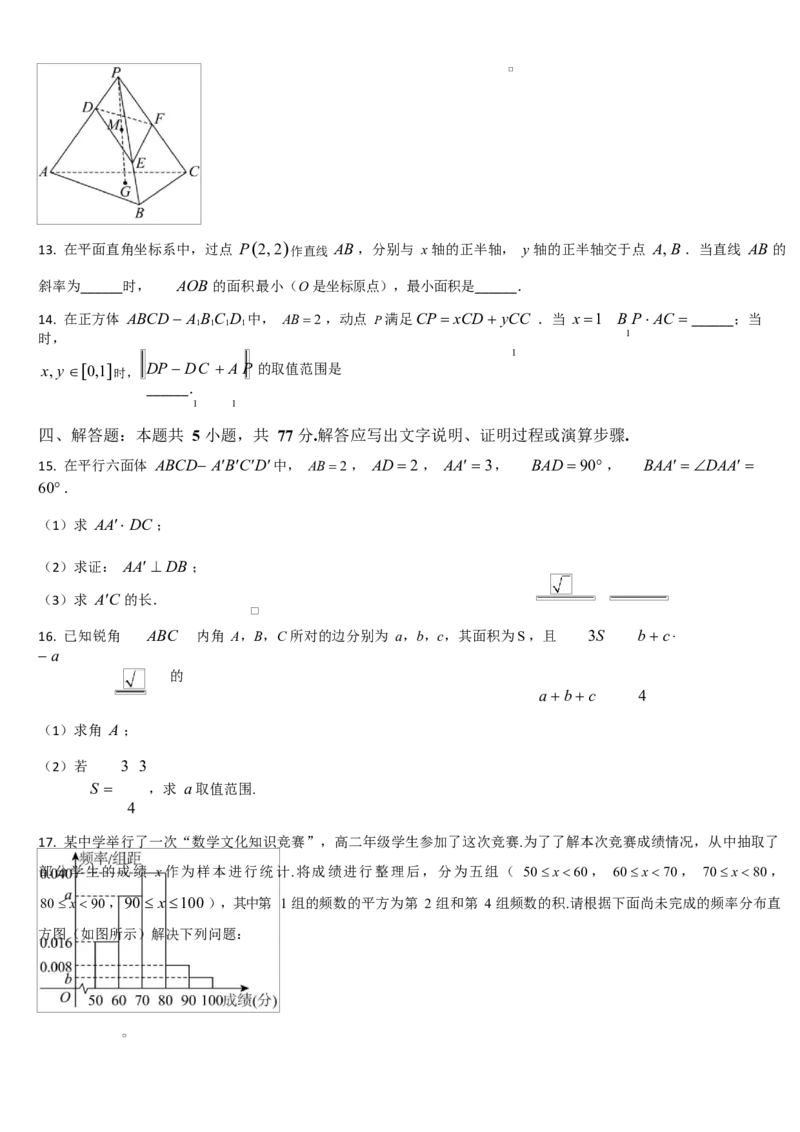
12. 如图，已知三棱锥 P  ABC ，G 为 ABC 的重心，点 M ， F 为 PG ， PC 的中点，点 D,E 分别在 PA, PB
上，
3 2
PD  2mPA ， PE  3nPB(m  0,n  0) ．若 M,D,E,F 四点共面，
  ______．
则
m n13. 在平面直角坐标系中，过点 P2, 2 作直线 AB ，分别与 x 轴的正半轴， y 轴的正半轴交于点 A, B ．当直线 AB 的
斜率为______时， AOB 的面积最小（O 是坐标原点），最小面积是______．
14. 在正方体 ABCD  A BC D 中， AB  2 ，动点 P 满足CP  xCD  yCC ．当 x 1 B P  AC  ______；当
1 1 1 1
时， 1
1
x, y 0,1 时， DP  DC  A P 的取值范围是
______．
1 1
四、解答题：本题共 5 小题，共 77 分.解答应写出文字说明、证明过程或演算步骤.
15. 在平行六面体 ABCD ABCD中， AB  2 ， AD  2 ， AA  3， BAD  90 ， BAA  DAA 
60．
（1）求 AA DC ；
（2）求证： AA  DB ；
（3）求 AC 的长．
16. 已知锐角 ABC 内角 A，B，C 所对的边分别为 a，b，c，其面积为S ，且 3S b  c .
 a
的 
a  b  c 4
（1）求角 A ；
（2）若 3 3
S  ，求 a 取值范围.
4
17. 某中学举行了一次“数学文化知识竞赛”，高二年级学生参加了这次竞赛.为了了解本次竞赛成绩情况，从中抽取了
部分学生的成绩 x 作为样本进行统计.将成绩进行整理后，分为五组（ 50  x  60 ， 60  x  70 ， 70  x  80 ，
80  x  90 ，90  x 100 ），其中第 1 组的频数的平方为第 2 组和第 4 组频数的积.请根据下面尚未完成的频率分布直
方图（如图所示）解决下列问题：（1）若根据这次成绩，年级准备淘汰 60%的同学，仅留 40%的同学进入下一轮竞赛，请问晋级分数线划为多少合理？（2）从样本数据在80  x  90 ，90  x 100 两个小组内的同学中，用分层抽样的方法抽取 6 名同学，再从这 6 名同学
中随机选出 2 人，求选出的两人恰好来自不同小组的概率．
（3）某老师在此次竞赛成绩中抽取了 10 名学生的分数： x , x , x , , x ，已知这 10 个分数的平均数 x  90 ，标准
1 2 3 10
差 s  5，若剔除其中的 96 和 84 两个分数，求剩余 8 个分数的平均数与方差．
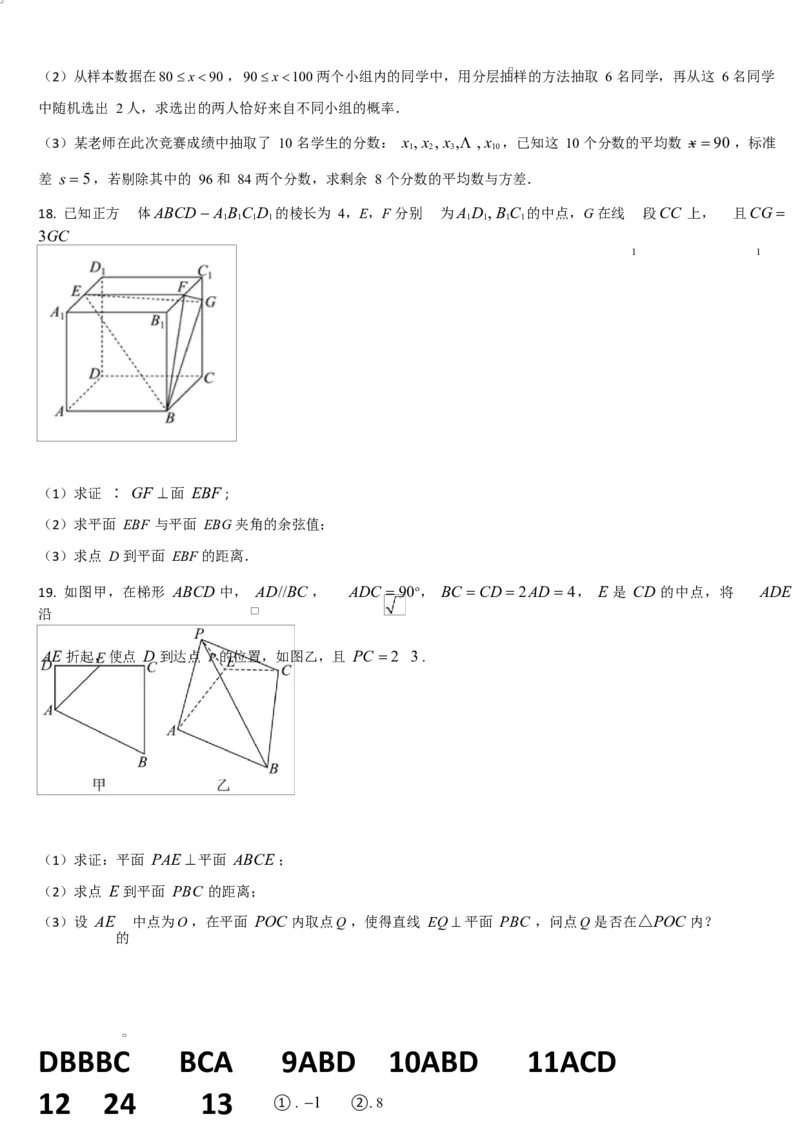
18. 已知正方 体ABCD  A BC D 的棱长为 4，E，F 分别 为A D , BC 的中点，G 在线 段CC 上， 且CG 
1 1 1 1 1 1 1 1
3GC
1 1
（1）求证 ∶ GF 面 EBF ;
（2）求平面 EBF 与平面 EBG 夹角的余弦值；
（3）求点 D 到平面 EBF 的距离．
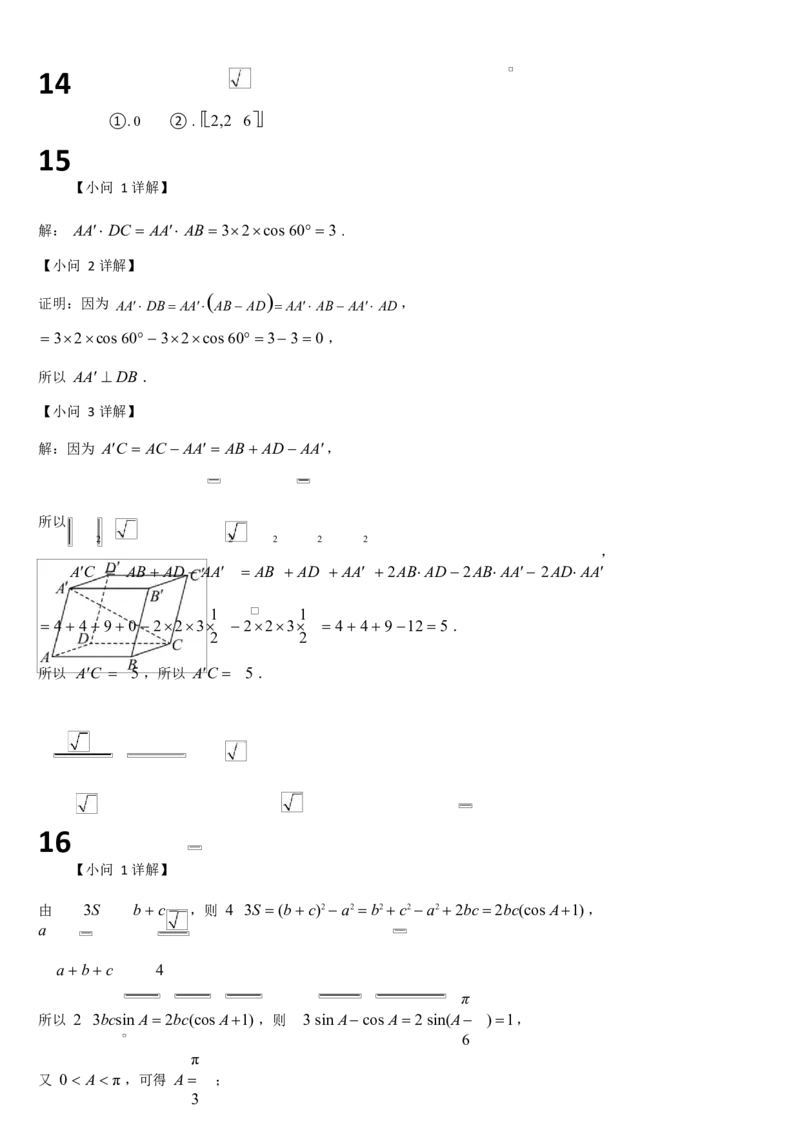
19. 如图甲，在梯形 ABCD 中， AD//BC ， ADC  90， BC  CD  2AD  4， E 是 CD 的中点，将 ADE
沿
AE 折起，使点 D 到达点 P 的位置，如图乙，且 PC  2 3 .
（1）求证：平面 PAE 平面 ABCE ；
（2）求点 E 到平面 PBC 的距离；
（3）设 AE 中点为O ，在平面 POC 内取点Q ，使得直线 EQ  平面 PBC ，问点Q 是否在△POC 内？
的
DBBBC BCA 9ABD 10ABD 11ACD
12 24 13
① . 1 ②. 814
①. 0 ② . 2,2 6
15
【小问 1 详解】
解： AA DC  AA AB  32cos 60  3 .
【小问 2 详解】
 
证明：因为 AA DB  AA AB  AD  AA AB  AA AD ，
 32cos 60  32cos 60  3 3  0 ，
所以 AA  DB ．
【小问 3 详解】
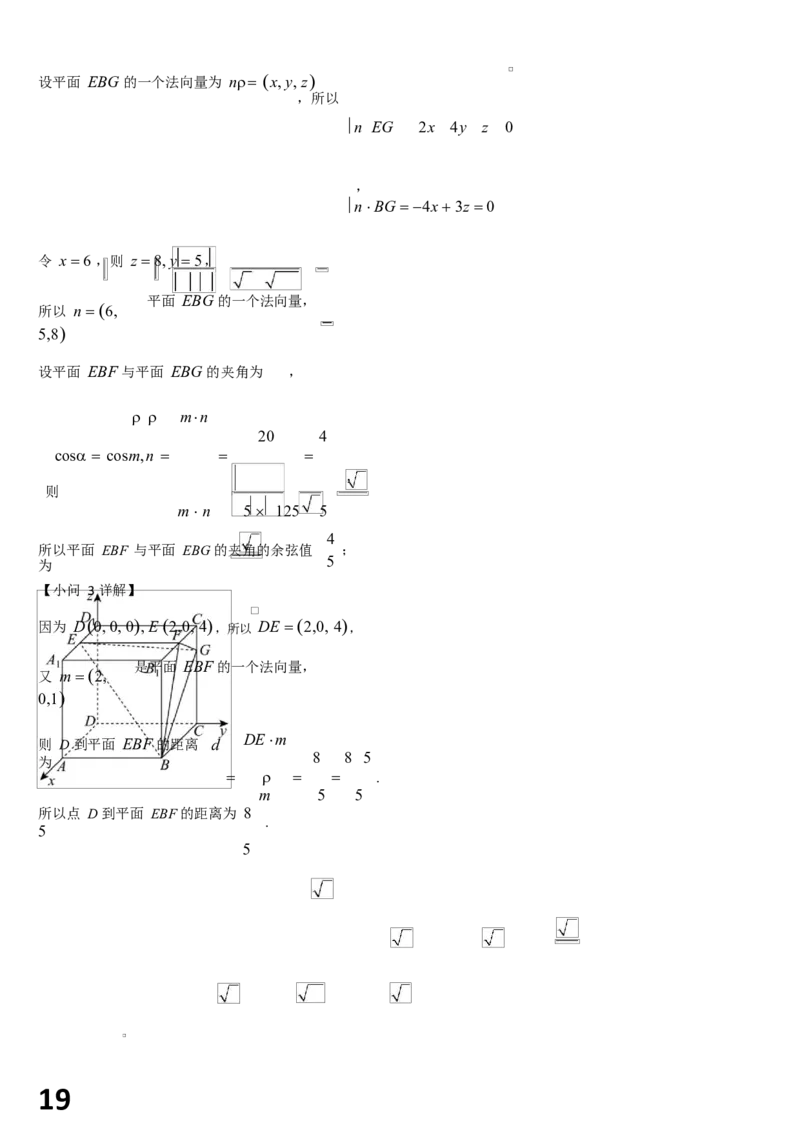
解：因为 AC  AC  AA  AB  AD  AA，
       
    
 
所以
2 2 2 2 2
，
AC  AB  AD  AA  AB  AD  AA  2AB AD  2AB AA 2AD AA
1 1
 4  4  9  0  223  223  4  4  9 12  5 ．
2 2
所以 AC  5 ，所以 AC  5 ．
16
【小问 1 详解】
由 3S b  c  ，则 4 3S  (b  c)2  a2  b2  c2  a2  2bc  2bc(cos A1) ，
a

a  b  c 4
π
所以 2 3bcsin A  2bc(cos A1) ，则 3 sin A cos A  2 sin(A ) 1，
6
π
又 0  A  π ，可得 A  ；
3【小问 2 详解】
B C    C  ，
C
π
由 1 sin 3 3 3
S  bc A   bc  ，且sin sin sin sin
 3 
2 4
a b c a2 bc
由正弦定理知
   2R   ，
sin A sin B sinC sin A sin BsinC
29 9 9 9
a2 
所以    π ，
2sin(2C  ) 1
   C C  2 C C  C 
6
π 2 3 sin cos 2 sin 3 sin 2 cos 2
1
4 sin C sinC
 
 3 

 
π  C  π ，则 π 2 π 5π
π
0 B  C   ，
 6 2 6 6 6
2π
2
π
B  C
且

由 ，可得
3

 
0 C


2
1  C  π  ，故3 9
所以 2
sin(2 ) 1 a .
 a  ，即 [ 3, 3 2 )
2 6 2 2
17
【小问 1 详解】
由第 1 组的频数的平方为第 2 组和第 4 组频数的积可知， 0.162  0.8a ，
解得 a  0.032 ，
又 0.008 0.016  0.032  0.04  b10 1，解得b  0.004，
所以 a  0.032 ，b  0.004，
成绩落在 50, 70 内的频率为： 0.16  0.32  0.48 ，
落在  50,80 内的频率为： 0.16  0.32  0.40  0.88，设第 60 百分位数为 m ，
则 m  700.04  0.6  0.48，解得 m  73，所以晋级分数线划为 73 分合理；
【小问 2 详解】
由图可知，按分层抽样法，两层应分别抽取 4 人和 2 人，分别记为 a ，b ， c ， d 和 A ， B ，
则所有的抽样有： Ω  AB, Aa, Ab, Ac, Ad, Ba, Bb, Bc, Bd,ab,ac,ad,bc,bd,cd  ，共 15 个样本点，
A  “抽到的两位同学来自不同小组”，则 A  Aa, Ab, Ac, Ad, Ba, Bb, Bc, Bd 共 8 个样本点，
8
所以 PA  .
15
【小问 3 详解】
因为 x  90 ，所 x  x   x 1090  900，
1 2 10
以
1
 
所以
s2  x2  x2   x2 902  52 ，
1 2 10
10
所以 x2  x2   x2  ，
81250
1 2 10
x ， x ， x ，…， x ，
剔除其中的 96 和 84 两个分数，设剩余 8 个数为 2 3 8
1平均数与标准差分别为 x ， s ，
0
0
   900 96 84 
x  x  x   x  
则剩余 8 个分数的平均数： x 1 2 3 8 90
，
0
8 8
1 1
   
方差：
s2  x2  x2   x2  2   2  2  2 
90 81250 96 84 90 22.25
0 1 2 8
8 8
18
【小问 1 详解】
（1）法一、在正方形 BCC B 中，
1 1
C G 1 FB
由条件易知
tan tan
1 1
C FG     B BF ，所以 C FG  B BF
，
1 1 1 1
C F 2 BB
1 1
π
B FB  B BF   C FG  B FB
， 则
1 1 1 1
2
π
故 BFG  C FG  B FB ，即 FG  BF ，
π
1 1
2
在正方体中，易知 DC  平 BCC B ，且 EF / /D C ，
1 1
1 1 1 1
面
所以 EF  平面 BCC B ，
1 1
又 FG  平面BCC B ，∴ EF  FG
，
1 1
EF  BF  F ， EF, BF  平面 EBF ，∴GF  平面 EBF ；
∵法二、如图以 D 为原点建立空间直角坐标系，
则 B4, 4,0, E 2,0, 4, F 2, 4, 4,G0, 4,3 ，
所以 EF  0, 4,0, EB  2,4,4, FG  2,0,1 ，

是平面 EBF 的法向量，设 m 
a,b,c

   
m EF 4b 0
   ，令 a  2，则b  0,c 1，
则
m EB  2a  4b  4c 
0 

是平面 EBF 的一个法向量，
所以 m  2,
0,1
易知 FG  m
，则 FG 也是平面 EBF 的一个法向量，∴GF  平面 EBF ；
【小问 2 详解】
同上法二建立的空间直角坐标系，
所以 EG  2,4,1, BG  4, 0, 3 ，

是平面 EBF 的一个法向量，
由（1）知 m  2,
0,1
设平面 EBG 的一个法向量为 n x, y, z     
，所以
 
n EG 2x 4y z 0
 

，
n  BG  4x  3z  0

令 x  6 ，则 z  8, y  5，

平面 EBG 的一个法向量，
所以 n  6,
5,8
设平面 EBF 与平面 EBG 的夹角为 ，
 
  mn
20 4
cos  cosm,n   
  ，
则
m  n 5  125 5
4
所以平面 EBF 与平面 EBG 的夹角的余弦值 ；
5
为
【小问 3 详解】
因为 D0, 0, 0, E 2,0, 4 ，所以 DE  2,0, 4 ，

是平面 EBF 的一个法向量，
又 m  2,
0,1

DE m
则 D 到平面 EBF 的距离 d
8 8 5
为
    .
m 5 5
所以点 D 到平面 EBF 的距离为 8
.
5
5
19【小问 1 详解】
取 AE 的中点O ，连结OP ，OC ，因为 PA  PE ，所以OP  AE ，
在 Rt APE 中， AP  PE  2，所以OP  2 ，
 
在△OEC 中，OC  OE  CE  2OE CEcos135  2  2  2 2 2  10
，
2
 
在△POC 中 ，OP  OD  2 ，OC  10 ， PC  2 3 ，所以
OP2  OC2  PC2 ，
所以OP  OC ，又因为 AE OC  O， AE，OC  平面 ABCE ，所以OP  平面 ABCE ，又 OP  平面 PAE ，所以平面 PAE 平面 ABCE .
【小问 2 详解】
连结OB ， BE ， BE  BC2  CE2  42  22  2 5 ，
 2  2
AB  CD2  BC  AD  42  4  2  2 5 ，所以OB  AE ，
且 OB  BE2 OE2  20  2  3 2 ，由（1）可知OP  平面 ABCE ，
又因为OA，OB  平面 ABCE ，
所以OP  OA，OP  OB ，所以OP，OA，OB 两两垂直，
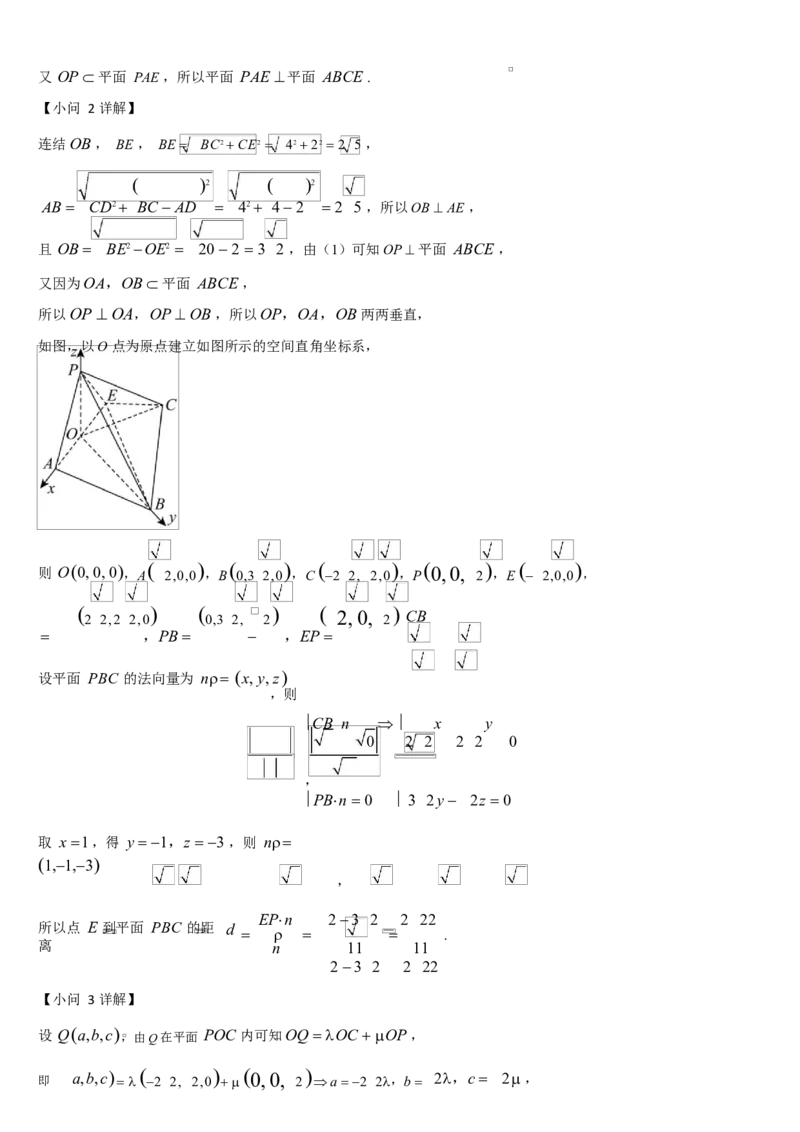
如图，以O 点为原点建立如图所示的空间直角坐标系，
则 O0, 0, 0，A  2,0,0  ，B  0,3 2,0  ，C  2 2, 2,0  ，P 0, 0, 2  ，E   2,0,0  ，
 2 2,2 2,0   0,3 2, 2   2, 0, 2  CB
 ，PB   ，EP  ，

设平面 PBC 的法向量为 n x, y, z     
，则

CB n   x y
0 2 2 2 2 0
   
，
PBn  0  3 2y  2z  0
 
取 x 1，得 y  1，z  3 ，则 n
1,1,3
，
 
EPn 2 3 2 2 22
所以点 E 到平面 PBC 的距 d
    .
离 n 11 11
2 3 2 2 22
【小问 3 详解】
设 Qa,b,c ，由Q 在平面 POC 内可知OQ  OC  OP ，
即 a,b,c    2 2, 2,0    0, 0, 2   a  2 2，b  2，c  2 ，
a Qa  a c EQ  a   c
a
b   ，即 , , ，所以 2, , 所
以 ，
2  2   2 
因为 EQ  平面 PBC ，所以 EQ是平面 PBC 的一个法向量，所以 EQ / /n
，a ，解得 a  2 2，c  3 2 ，故Q  2 2, 2,3 2  ，
a   c
即 2  2 
1 1 3
而 C  2 2, 2,0  ，可知Q 点不在 △POC 内.