文档内容
2004 年江苏高考数学真题及答案
一、选择题(5分×12=60分)
1.设集合P={1,2,3,4},Q={ },则P∩Q等于 ( )
(A){1,2} (B) {3,4} (C) {1} (D) {-2,-1,0,1,2}
2.函数y=2cos2x+1(x∈R)的最小正周期为 ( )
(A) (B) (C) (D)
3.从4名男生和3名女生中选出4人参加某个座谈会,若这4人中必须既有男生又有女生,则不同的选法
共有 ( )
(A)140种 (B)120种 (C)35种 (D)34种
4.一平面截一球得到直径是 6cm 的圆面,球心到这个平面的距离是 4cm,则该球的体积是
( )
(A) (B) (C) (D)
5. 若 双 曲 线 的 一 条 准 线 与 抛 物 线 的 准 线 重 合 , 则 双 曲 线 的 离 心 率 为
( )
(A) (B) (C) 4 (D)
6.某校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的
数据,结果用右侧的条形图表示. 根据条形图可得这 50 名学生这一天平均每人的课外阅读时间为
( )
(A)0.6小时 (B)0.9小时 (C)1.0小时 (D)1.5小时
人数(人)
20
15
10
5
0 0.5 1.0 1.5 2.0 时间(小时)
7. 的展开式中x3的系数是 ( )
(A)6 (B)12 (C)24 (D)48
8.若函数 的图象过两点(-1,0)和(0,1),则 ( )
(A)a=2,b=2 (B)a=,b=2 (C)a=2,b=1 (D)a=,b=
9.将一颗质地均匀的骰子(它是一种各面上分别标有点数1,2,3,4,5,6的正方体玩具)先后抛掷3次,
至少出现一次6点向上的概率是 ( )
(A) (B) (C) (D)
10.函数 在闭区间[-3,0]上的最大值、最小值分别是 ( )
(A)1,-1 (B)1,-17 (C)3,-17 (D)9,-19
第1页 | 共6页11.设k>1,f(x)=k(x-1)(x∈R) . 在平面直角坐标系xOy中,函数y=f(x)的图象与x轴交于A点,它的反
函数y=f -1(x)的图象与y轴交于B点,并且这两个函数的图象交于P点. 已知四边形OAPB的面积是3,则
k等于 ( )
(A)3 (B) (C) (D)
12.设函数 ,区间M=[a,b](a0的解集是_______________________.
14.以点(1,2)为圆心,与直线4x+3y-35=0相切的圆的方程是________________.
15.设数列{a}的前 n 项和为 S ,S= (对于所有 n≥1),且 a=54,则 a 的数值是
n n n 4 1
_______________________.
16.平面向量a,b中,已知a=(4,-3), =1,且ab=5,则向量b=__________.
三、解答题(12分×5+14分=74分)
17.已知0<α< ,tan +cot = ,求sin( )的值.
18.在棱长为4的正方体ABCD-ABCD 中,O是正方形ABCD 的中心,点P在棱CC 上,且CC=4CP.
1 1 1 1 1 1 1 1 1 1
(Ⅰ)求直线AP与平面BCCB 所成的角的大小(结果用反三角函数值表示);
1 1
(Ⅱ)设O点在平面DAP上的射影是H,求证:DH⊥AP;
1 1
D
(Ⅲ)求点P到平面ABD 的距离. 1 C
1 1
· O
A 1 B 1
·
H
P
D
C
A B
19.制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.
某投资人打算投资甲、乙两个项目. 根据预测,甲、乙项目可能的最大盈利率分别为100﹪和50﹪,可
能的最大亏损分别为30﹪和10﹪. 投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过
1.8万元. 问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
第2页 | 共6页20.设无穷等差数列{a}的前n项和为S.
n n
(Ⅰ)若首项 ,公差 ,求满足 的正整数k;
(Ⅱ)求所有的无穷等差数列{a},使得对于一切正整数k都有 成立.
n
21.已知椭圆的中心在原点,离心率为,一个焦点是 F(-m,0)(m是大于0的常数). (Ⅰ)求椭圆的方
程; (Ⅱ)设Q是椭圆上的一点,且过点F、Q的直线 与y轴交于点M. 若 ,求直线 的斜率.
22.已知函数 满足下列条件:对任意的实数x,x 都有
1 2
和 , 其中 是大于0的常数.
设实数a,a,b满足 和
0
(Ⅰ)证明 ,并且不存在 ,使得 ;
(Ⅱ)证明 ;
(Ⅲ)证明 .
2004年高考数学江苏卷答案
一、 选择题
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A B D C A B C A D C B A
二、 填空题
13、 ; 14、 ;
15、2; 16、
第3页 | 共6页三、 解答题
(17)由已知得: 得 , , ,从
而
(18)
( 1 ) 连 结 BP , 平 面 , 与 平 面 所 成 角 就 是 ,
,在 中, 为直角, ,故 ,在
中, 为直角, , ,即直线AP与平面
所成角为 。
( 2)连结 ,四边形 是正方形, ,又 平面
, , , 平面 ,由于 平面
,又平面 的斜线 在这个平面内的射影是 , .
(3)连结 ,在平面 中,过点P作 于点Q,AB⊥平面 ,PQ 平面 ,
PQ⊥ AB , PQ⊥ 平 面 , PQ 就 是 点 P 到 平 面 ABD 的 距 离 , 在 中 ,
1
, ,即点P到平面ABD 的距离为 。
1
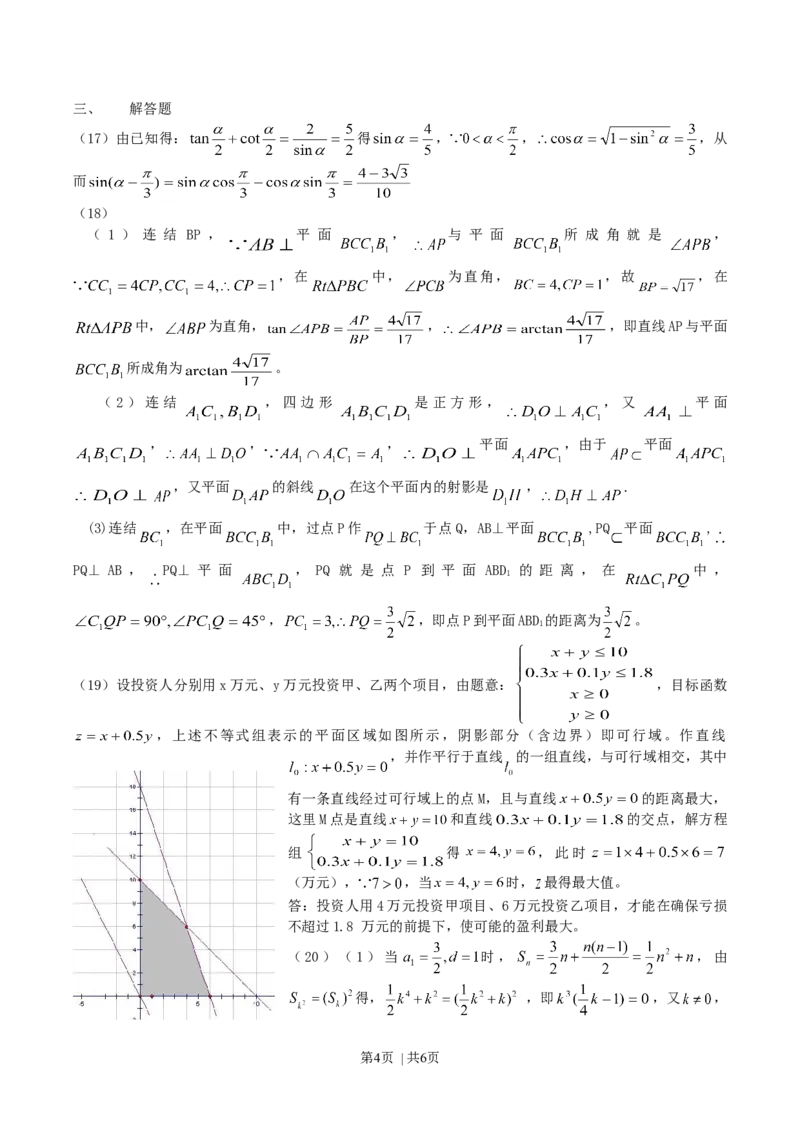
(19)设投资人分别用x万元、y万元投资甲、乙两个项目,由题意: ,目标函数
,上述不等式组表示的平面区域如图所示,阴影部分(含边界)即可行域。作直线
,并作平行于直线 的一组直线,与可行域相交,其中
有一条直线经过可行域上的点M,且与直线 的距离最大,
这里M点是直线 和直线 的交点,解方程
组 得 ,此时
(万元), ,当 时, 最得最大值。
答:投资人用4万元投资甲项目、6万元投资乙项目,才能在确保亏损
不超过1.8 万元的前提下,使可能的盈利最大。
(20)(1)当 时, ,由
得, ,即 ,又 ,
第4页 | 共6页所以 。
( 2 ) 设 数 列 的 公 差 为 , 则 在 中 分 别 取 得 即
,由(1)得 或 。
当 时,代入(2)得: 或 ;
当 时, ,从而 成立;
当 时,则 ,由 , 知, ,故所得数列不符
合题意;
当 时, 或 ,当 , 时, ,从而 成立;当 ,
时,则 ,从而 成立,综上共有 3个满足条件的无穷等差数列; 或
或 。
(21)(1)设所求椭圆方程是 由已知得 ,所以 ,故所
求椭圆方程是
(2)设 ,直线 ,则点 ,当 时,由于 ,
,由定比分点坐标公式得 ,又点 在椭圆
上,所以 , ;当 时
,所以 得,解得 ,故直线 的斜率是
。
(22)证明:(1)任取 ,则由 ①
和 ②
可知, ,从而 ;
第5页 | 共6页假设有 ,使得 ,则由①式知, ,矛盾,因此不
存在 ,使得 。
(2)由 ③可知
④
由 和①得, ⑤
由 和②得, ⑥
将⑤⑥代入④得 ;
(3)由③式可知,
(用②式)
(用①式)
。
第6页 | 共6页