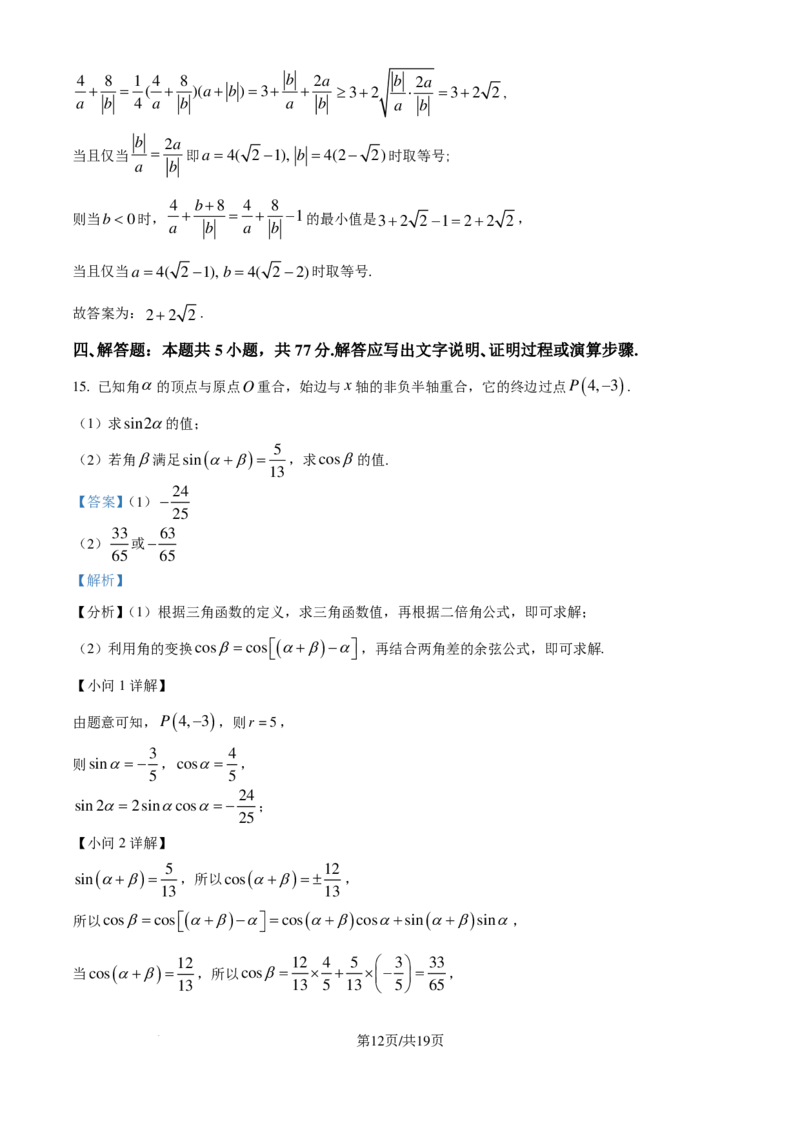文档内容
江门市 2025 届普通高中高三调研测试
数学
本试卷共 5页,19小题,满分 150分.考试时间 120分钟.
注意事项:
1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上,
2.做选择题时,必须用2B铅笔将答题卷上对应题目的答案标号涂黑;如需改动,用橡皮擦干
净后,再选涂其它答案标号.
3.答非选择题时,必须用黑色字迹钢笔或签字笔,将答案写在答题卡规定的位置上.
4.所有题目必须在答题卡上作答,在试题卷上作答无效.
5.考试结束后,将答题卡交回.
一、选择题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
A= { x∈N∣0≤ x2 ≤9 } ,B={ x∈N∣0≤ x≤10 }
AB =
1. 已知集合 ,则 ( )
A. { x∣0≤ x≤9 } B. { 1,2,3 }
C. { x∣0≤ x≤3 } D. { 0,1,2,3 }
【答案】D
【解析】
【分析】根据题意求集合A,B,集合交集运算求解.
【详解】由题意可得:A= { x∈N∣0≤ x2 ≤9 } ={ 0,1,2,3 } ,
B={ x∈N∣0≤ x≤10 }={ 0,1,2,3,4,5,6,7,8,9,10 } ,
所以A∩B={
0,1,2,3
}
.
故选:D.
2. 设m,n∈R,则“(m+1)3 =n3”是“2m 2n”的( )
A. 充分不必要条件 B. 充要条件
C. 必要不充分条件 D. 既不充分又不必要条件
【答案】A
【解析】
第1页/共19页
学科网(北京)股份有限公司【分析】根据充分、必要条件的判定方法进行判断.
【详解】由( m+1 )3 =n3 ⇒ m+1=n ⇒ 2m+1 =2n,
又2m <2m+1,所以2m 2n,故“(m+1)3 =n3”是“2m 2n”的充分条件;
又若2m 2n,如m=0,n=2,此时(m+1)3 =n3不成立,
所以“(m+1)3 =n3”是“2m 2n”的不必要条件.
综上:“(m+1)3 =n3”是“2m 2n”的充分不必要条件.
故选:A
3. 下列命题为真命题的是( )
a a+c
A. 若a>b>c>0,则 <
b b+c
c c
B. 若a>b>0,c<0,则 <
a b
C. a>b>0,则ac2 >bc2
a+b
D. 若a>b,则a > >b
2
【答案】D
【解析】
【分析】根据不等式的性质作差法比较大小或取特殊值判断,即可得出结果.
a a+c a ( b+c )−b ( a+c ) c ( a−b )
【详解】对于A, − = = ,
b b+c b ( b+c ) b ( b+c )
因为 a>b>c>0,所以a−b>0,b ( b+c )>0,
a a+c c ( a−b ) a a+c
所以 − = >0,即 > ,故A错误;
b b+c b ( b+c ) b b+c
1 1
对于B,因为a>b>0,所以 < ,
a b
c c
又c<0,所以 > ,故B错误;
a b
对于C,当c=0时,ac2 =bc2 =0,故C错误;
对于D,若a>b,则2a >a+b,a+b>2b,
第2页/共19页
学科网(北京)股份有限公司a+b
所以a > >b,故D正确.
2
故选:D.
ex +e−x,x≤2,
4. 已知函数 f
(
x
)=
x 则 f
(
ln27
)=(
)
f ,x>2,
3
8 10 728 730
A. B. C. D.
3 3 27 27
【答案】B
【解析】
【分析】利用对数的运算性质计算可得答案.
【详解】因为1=lne3,又因为 f
(
x
)=
x ,
f ,x>2
3
所以 f ( ln27 )= f ln27 = f 3ln3 = f ( ln3 )=eln3+e−ln3 =3+e ln 1 3 =3+ 1 = 10 .
3 3 3 3
故选:B.
π
5. 下列函数中,以π为周期,且在区间 ,π上单调递增的是( )
2
A. y =sin x B. y =cos x
C. y = tanx D. y = cosx
【答案】D
【解析】
【分析】先判断各函数的最小正周期,再确定各函数在区间上的单调性,即可选择判断.
π 3π
【详解】对于A:由sin − =1,sin − =−1,可知π不是其周期,(也可说明其不是周期函数)故错
2 2
误;
cosx,x≥0 cosx,x≥0
对于B:y =cos x = = =cosx,其最小正周期为2π,故错误;
cos (−x ) ,x<0 cosx,x<0
对于C:y = tanx 满足 tan ( x+π) = tanx ,以π为周期,
第3页/共19页
学科网(北京)股份有限公司π π
当x∈ ,π时,y = tanx =−tanx,由正切函数的单调性可知y = tanx =−tanx在区间 ,π上单
2 2
调递减,故错误;
对于D,y = cosx 满足 cos ( x+π ) = cosx ,以π为周期,
π π
当x∈ ,π时,y = cosx =−cosx,由余弦函数的单调性可知,y =−cosx在区间 ,π上单调递
2 2
增,故正确;
故选:D
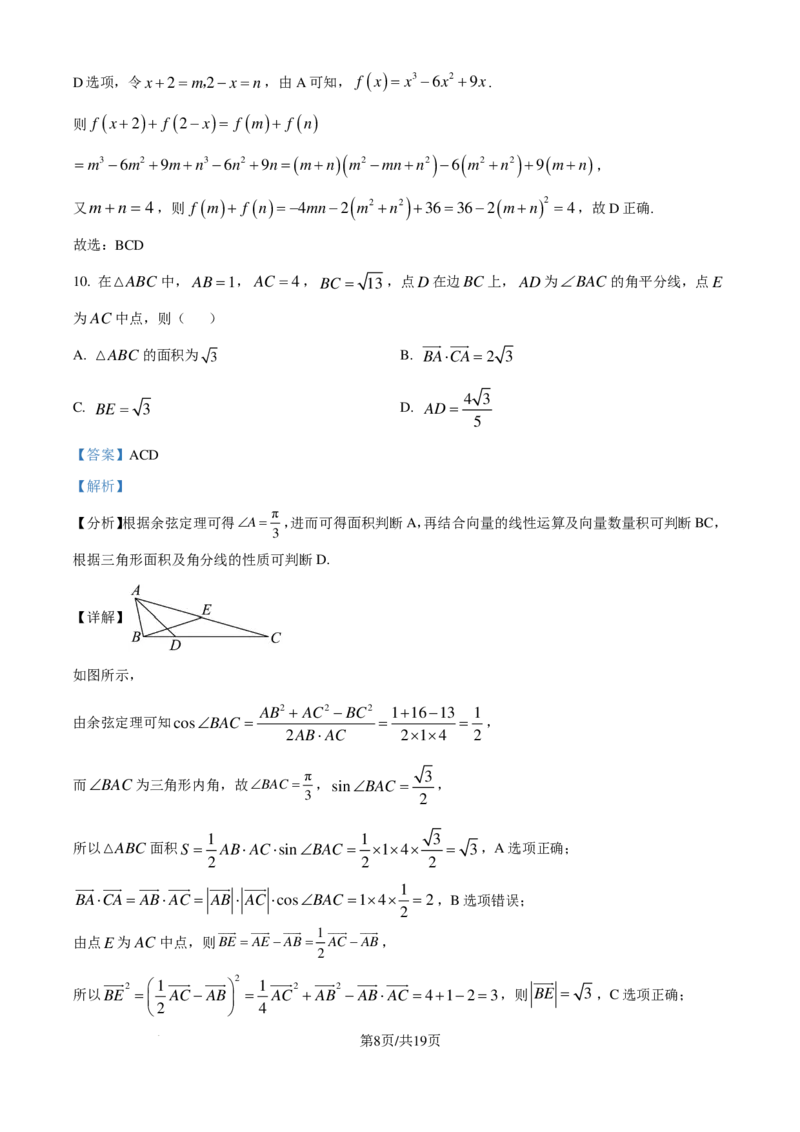
6. 在正方形ABCD中,AE = EB,FC =2BF,AF 与DE交于点M ,则cos∠EMF =( )
2 1 2 1
A. B. C. D.
5 5 10 10
【答案】C
【解析】
【分析】建立平面直角坐标系,利用向量的坐标计算夹角的余弦值即可.
【详解】
建立平面直角坐标系,设正方形ABCD的棱长为2,
因为AE = EB,FC =2BF ,
2
( ) ( ) ( )
则E 0,1 ,A 0,2 ,D 2,2 ,F ,0,
3
2
所以AF = ,−2,DE =(−2,−1 ),
3
4
− +2
3 2
所以cos∠EMF = cosAF,DE = =
.
40 10
5×
9
故选:C
第4页/共19页
学科网(北京)股份有限公司7. 金针菇采摘后会很快失去新鲜度,甚至腐烂,所以超市销售金针菇时需要采取保鲜膜封闭保存.已知金
针菇失去的新鲜度h与其来摘后时间t(天)满足的函数解析式为h=mln ( t+a )( a >0 ) .若采摘后1天,
金针菇失去的新鲜度为40%;若采摘后3天,金针菇失去的新鲜度为80%.现在金针菇失去的新鲜度为
60%,则采摘后的天数为( )(结果保留一位小数, 2 ≈1.41)
A. 1.5 B. 1.8 C. 2.0 D. 2.1
【答案】B
【解析】
【分析】根据已知条件得到两个等式,两个等式相除求出a的值,再根据两个等式相除可求得结果.
mln ( 1+a )=0.4 ln ( 3+a )
【详解】由题可得 ,两式相除可得 =2,
mln ( 3+a )=0.8 ln ( 1+a )
则ln ( 3+a )=2ln ( 1+a ) ,3+a =( 1+a )2,
∵a>0,解得a =1,
设t天后金针菇失去的新鲜度为60%,
则mln ( t+1 )=0.6,又mln ( 1+1 )=0.4,
∴ ln ( t+1 ) = 3 ,2ln ( t+1 )=3ln2,( t+1 )2 =23 =8,t+1=2 2 =2×1.41=2.82,
ln2 2
则t =2.82−1=1.82≈1.8,
故选:B.
8. 已知各项都为正数的数列 满足a =1,a =2,a2 −a2 −a a >a a ( n≥3,n∈N ) ,则下列
1 2 n n−1 n n−2 n−1 n−2 +
结论中一定正确的是( )
{ 𝑎𝑎𝑛𝑛}
A. a >124 B. a >1024
8 20
C. a <124 D. a <1204
8 20
【答案】B
【解析】
【分析】由a2 −a2 −a a >a a ( n≥3,n∈N ) 得 ( a +a )a −( a +a ) >0,由题意,
n n−1 n n−2 n−1 n−2 + n n−1 n n−1 n−2
a >a +a ,根据递推公式可验证B,通过对a 赋值,可验证ACD.
n n−1 n−2 3
【详解】由a2 −a2 −a a >a a ( n≥3,n∈N ) ,
n n−1 n n−2 n−1 n−2 +
第5页/共19页
学科网(北京)股份有限公司得 ( a
n
+a
n−1
)
a
n
−( a
n−1
+a
n−2
)
>0,
因为数列 各项都为正数,
所以a +{ a𝑎𝑎𝑛𝑛}>0,故a −( a +a )>0,即a >a +a ,
n n−1 n n−1 n−2 n n−1 n−2
所以a >a +a =2+1=3,
3 2 1
对于A,设a =4,则a >a +a =4+2=6,
3 4 3 2
设a =7,则a >a +a =7+4=11,
4 5 4 3
设a =12,则a >a +a =12+7=19,
5 6 5 4
设a =20,则a >a +a =20+12=32,
6 7 6 5
设a =33,则a >a +a =33+20=53,
7 8 7 6
则a 可以为54<124,故A错误;
8
对于B,a >a +a >3+2>5,a >a +a >5+3>8,
4 3 2 5 4 3
a >a +a >8+5>13,a >a +a >13+8>21,
6 5 4 7 6 5
a >a +a >21+13>34, a >a +a >34+21>55,
8 7 6 9 8 7
a >a +a >55+34>89,a >a +a >89+55>144,
10 9 8 11 10 9
a >a +a >144+89>233,a >a +a >233+144>377,
12 11 10 13 12 11
a >a +a >377+233>610,a >a +a >610+377>987,
14 13 12 15 14 13
a >a +a >987+610>1597,a >a +a >1597+987>2584,
16 15 14 17 16 15
a >a +a >2584+1597>4181,a >a +a >4181+2584>6765,
18 17 16 19 18 17
a >a +a >6765+4184>10946>1024,故B正确;
20 19 18
对于C,若a =124, 由于a >a +a ,则a >124,故C错误;
3 n n−1 n−2 8
对于D,若a =1024, 由于a >a +a ,则a >1024,故D错误;
3 n n−1 n−2 20
故选:B
二、多选题:本题共 3小题,每小题 6分,共 18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得 6分,部分选对的得部分分,有选错的得 0分.
第6页/共19页
学科网(北京)股份有限公司9. 若函数 f ( x )= x(x−c)2在x=1处取得极大值,则( )
A. c=1,或c=3
B. xf ( x+1 )<0的解集为 (−1,0 )
C. 当0 f ( cos2x )
2
D. f ( 2+x )+ f ( 2−x )=4
【答案】BCD
【解析】
【分析】A选项,由题可得
f′(
1
)=0,据此得c的可能值,验证后可判断选项正误;B选项,由A分析,
可得xf ( x+1 ) 表达式,解相应不等式可判断选项正误;C选项,由A分析结合cosx,cos2x大小关系可判
断选项正误;D选项,由A分析,验证等式是否成立可判断选项正误.
【详解】A选项,由题 f ( x )= x3 −2cx2 +c2x,则 f′( x )=3x2 −4cx+c2,
因在x=1处取得极大值,则 f′( 1 )=c2 −4c+3=0⇒c=1或c=3.
1 1
当c=1时, f′( x )=3x2 −4x+1,令 f′( x )>0⇒ x∈ −∞, ∪( 1,+∞) ; f′( x )<0⇒ x∈ ,1.
3 3
1 1
则 f ( x ) 在 −∞, ,( 1,+∞) 上单调递增,在 ,1上单调递减,则 f ( x ) 在x=1处取得极小值,不合题
3 3
意;
当c=3时, f′( x )=3x2 −12x+9,令 f′( x )>0⇒ x∈(−∞,1 )∪( 3,+∞) ; f′( x )<0⇒ x∈( 1,3 ) .
则 f
(
x
)
在
(−∞,1 ),( 3,+∞)
上单调递增,在
(
1,3
)
上单调递减,则 f
(
x
)
在x=1处取得极大值,满足题
意;
则c=3,故A错误;
B选项,由A可知, f ( x )= x ( x−3 )2,则
xf ( x+1 )= x ( x+1 )( x−2 )2 <0⇒ x ( x+1 )<0⇒ x∈(−1,0 ) .
故B正确;
π ( )
C选项,当0 f ( cos2x ) ,故C正确; (0,1)
第7页/共19页
学科网(北京)股份有限公司D选项,令x+2=m,2−x=n,由A可知, f ( x )= x3−6x2 +9x.
则 f ( x+2 )+ f ( 2−x )= f ( m )+ f ( n )
=m3 −6m2 +9m+n3 −6n2 +9n=( m+n )( m2 −mn+n2 ) −6 ( m2 +n2 ) +9 ( m+n ) ,
又m+n = 4,则 f ( m )+ f ( n )=−4mn−2 ( m2 +n2 ) +36=36−2 ( m+n )2 =4,故D正确.
故选:BCD
10. 在ABC中,AB =1,AC =4,BC = 13,点D在边BC上,AD为∠BAC的角平分线,点E
为AC中点,则( )
A. ABC的面积为 3 B. BA⋅CA=2 3
4 3
C. BE = 3 D. AD=
5
【答案】ACD
【解析】
π
【分析】根据余弦定理可得∠A= ,进而可得面积判断A,再结合向量的线性运算及向量数量积可判断BC,
3
根据三角形面积及角分线的性质可判断D.
【详解】
如图所示,
AB2 + AC2 −BC2 1+16−13 1
由余弦定理可知cos∠BAC = = = ,
2AB⋅AC 2×1×4 2
π 3
而∠BAC为三角形内角,故∠BAC = ,sin∠BAC = ,
3 2
1 1 3
所以ABC面积S = AB⋅AC⋅sin∠BAC = ×1×4× = 3,A选项正确;
2 2 2
1
BA⋅CA= AB⋅AC = AB ⋅ AC ⋅cos∠BAC =1×4× =2,B选项错误;
2
1
由点E为AC中点,则BE= AE−AB= AC−AB,
2
2
所以BE 2 = 1 AC−AB = 1 AC 2 + AB 2 −AB⋅AC =4+1−2=3,则 BE = 3,C选项正确;
2 4
第8页/共19页
学科网(北京)股份有限公司π
由AD为∠BAC的角平分线,则∠BAD=∠CAD= ,
6
1
所以S = AB⋅AD⋅sin∠BAD+ AC⋅AD⋅sin∠CAD,
2
1 1 1 1 5 4 3
即 3 = ×1× AD+ ×4× AD= AD,则AD= ,D选项正确;
2 2 2 2 4 5
故选:ACD.
11. 已知 f ( x )=sin2nx+cos2nx ( n∈N ) ,则( )
n +
π
( )
A. f x 的最小正周期为
2
2
k π
B. f ( x ) 的图象关于点 + ,0 ( k∈Z ) 对称
2 2 8
( ) π
C. f x 的图象关于直线x= 对称
n 2
1
D. ≤ f ( x )≤1
2n−1 n
【答案】ACD
【解析】
【分析】用函数对称性的定义及函数周期性的定义可判断ABC选项的正误;利用导数法可判断D选项的
正误.
( )2 1
【详解】 f (x)=sin4 x+cos4 x= sin2 x+cos2 x −2sin2 xcos2 x=1− sin22x
2 2
1 1−cos4x 3+cos4x
=1− × = ,
2 2 4
2π π
所以 f(x)的最小正周期为T= = ,故A正确;
4 2
π π kπ kπ π 3
令4x= +kπ,可得x= + ,k∈Z,所以 f ( x ) 的图象关于点 + , ( k∈Z ) 对称,故B错误;
2 8 4 2 4 8 4
对于C: f (π−x )=
sin (π−x )
2n +
cos (π−x )
2n =( sinx )2n +(−cosx )2n
=sin2n x+cos2n x= f ( x ) ,
π
所以函数 f ( x ) 的图象关于直线x= 对称,C对;
2
2n 2n
π π π
对于D: ,因为 f +x = sin +x + cos +x =( cosx )2n +(−sinx )2n
2 2 2
=sin2n x+cos2n x= f ( x ) ,
第9页/共19页
学科网(北京)股份有限公司π
( ) ( )
所以,函数 f x 为周期函数,且 是函数 f x 的一个周期,
2
π
( ) ( )
只需求出函数 f x 在
0,
上的值域,即为函数 f x 在R 上的值域,
2
f ( x )=sin2n x+cos2n x,则
f′( x )=2nsin2n−1xcosx−2ncos2n−1xsinx=2nsinxcosx ( sin2n−2 x−cos2n−2 x ) ,
π π 2
当x∈ , 时,0cos2n−2 x,此时 ,
′
𝑓𝑓 (𝑥𝑥)>0
π π
( )
所以,函数 f x 在
,
上单调递增,
4 2
π 2
当x∈ 0, 时,00,所以 f (−x )=sin (−x )
1+cos (−x )
=−sinx ( 1+cosx ) ,
又函数 f ( x ) 是定义在R上的偶函数,所以 f ( x )= f (−x )=−sinx ( 1+cosx ) .
故答案为:−sinx ( 1+cosx ) .
4 b+8
14. 已知a >0,b≠0,且a+ b =4,则 + 的最小值为__________.
a b
【答案】2+2 2 .
【解析】
4 b+8 4 8 b 4 8
【分析】先将所求式子化简 + = + + ,再根据基本不等式得到 + 的最小值,则可判断当
a b a b b a b
b<0,求得最小值.
4 b+8 4 8 b
【详解】根据题意: + = + + ,
a b a b b
b b
若b>0,则 =1, 若b>0,则 =−1,
|b| |b|
因为a >0,b≠0,则|b|>0,
第11页/共19页
学科网(北京)股份有限公司4 8 1 4 8 b 2a b 2a
+ = ( + )(a+ b)=3+ + ≥3+2 ⋅ =3+2 2,
a b 4 a b a b a b
b 2a
当且仅当 = 即a =4( 2−1), b =4(2− 2)时取等号;
a b
4 b+8 4 8
则当b<0时, + = + −1的最小值是3+2 2−1=2+2 2,
a b a b
当且仅当a=4( 2−1), b=4( 2−2)时取等号.
故答案为:2+2 2 .
四、解答题:本题共 5小题,共 77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知角α的顶点与原点O重合,始边与x轴的非负半轴重合,它的终边过点P ( 4,−3 ) .
(1)求sin2α的值;
5
(2)若角β满足sin (α+β)= ,求cosβ的值.
13
24
【答案】(1)−
25
33 63
(2) 或−
65 65
【解析】
【分析】(1)根据三角函数的定义,求三角函数值,再根据二倍角公式,即可求解;
(2)利用角的变换cosβ=cos
(α+β)−α
,再结合两角差的余弦公式,即可求解.
【小问1详解】
由题意可知,P ( 4,−3 ) ,则r =5,
3 4
则sinα=− ,cosα= ,
5 5
24
sin2α=2sinαcosα=− ;
25
【小问2详解】
5 12
sin (α+β)= ,所以cos (α+β)=± ,
13 13
所以cosβ=cos
(α+β)−α
=cos (α+β) cosα+sin (α+β) sinα,
12 12 4 5 3 33
当cos (α+β)= ,所以cosβ= × + × − = ,
13 13 5 13 5 65
第12页/共19页
学科网(北京)股份有限公司12 12 4 5 3 63
当cos (α+β)=− ,所以cosβ= − × + × − =− ,
13 13 5 13 5 65
33 63
综上可知,cosβ的值为 或−
65 65
16. 已知数列 { a } 的前n项和为S ,且3S =4n+1−4 ( n∈N ) .
n n n +
{ }
(1)证明:数列 log a 为等差数列;
2 n
1 1 1 1 100
(2)记数列 { log a } 的前n项和为T ,若 + + ++ < ,求满足条件的最大整数n.
2 n n T T T T 101
1 2 3 n
【答案】(1)证明见解析
(2)99
【解析】
【分析】(1)利用退一相减法可得a 及log a ,即可得证;
n 2 n
1 1 1 1
(2)根据等差数列求和公式可得T =n ( n+1 ) ,则 = = − ,利用裂项相消法可得
n T n ( n+1 ) n n+1
n
1 1 1 1 1
+ + ++ =1− ,解不等式即可.
T T T T n+1
1 2 3 n
【小问1详解】
由已知3S =4n+1−4,
n
当n=1时,3a =3S =42 −4=12,即a =4;
1 1 1
当n≥2时,3S =4n −4,
n−1
则3a =3S −3S =4n+1−4−4n +4=3⋅4n,即a =4n,
n n n−1 n
又n=1时,a =4满足a =4n,
1 n
所以a =4n =22n,
n
设b =log a =log 22n =2n,b −b =2 ( n+1 )−2n=2,
n 2 n 2 n+1 n
{ }
即数列 为等差数列,即数列 log a 为以2为首项2为公差的等差数列;
2 n
【小问
{
2
𝑏𝑏𝑛𝑛
详
}
解】
( b +b ) n ( 2+2n ) n
由等差数列可知T = 1 n = =n ( n+1 ),
n 2 2
第13页/共19页
学科网(北京)股份有限公司1 1 1 1
则 = = − ,
T n ( n+1 ) n n+1
n
1 1 1 1 1 1 1 1 1 1
所以 + + ++ =1− + − ++ − =1− ,
T T T T 2 2 3 n n+1 n+1
1 2 3 n
1 100
即1− < ,n∈N ,
n+1 101 +
解得n<100,
即满足条件的最大整数n=99.
17. 已知ABC的三个内角A,B,C 所对的边分别为a,b,c,且a =4,c=3b,记ABC的面积为S,内
切圆半径为r ,外接圆半径为R.
(1)若b= 2 ,求sinA;
1 S
(2)记 p= ( a+b+c ),证明:r = ;
2 p
(3)求rR的取值范围:
2 2
【答案】(1)
3
3
(2)证明见解析 (3) ,2
4
【解析】
【分析】(1)利用余弦定理求得cosA,进而求得sin A.
(2)根据三角形的面积公式证得结论成立.
(3)用b表示rR,然后利用导数求得rR的取值范围.
【小问1详解】
∵a=4,b= 2 ,c =3 2,
b2 +c2 −a2 2+18−16 1
由余弦定理,得cosA= = = ,
2bc 2× 2×3 2 3
2 2
∵0< A<π,∴sinA= 1−cos2 A = .
3
【小问2详解】
∵ABC的面积为S,内切圆半径为r ,
第14页/共19页
学科网(北京)股份有限公司1 1 1 1
∴S = a×r+ b×r+ c×r = ( a+b+c ) r ,
2 2 2 2
1 S
又∵ p = (a+b+c),∴S = pr,∴r = .
2 p
【小问3详解】
a a 4 2
由正弦定理得 =2R,得R= = = ,
sinA 2sinA 2sinA sinA
因为a=4,c=3b,
1
由(2)得S = pr = r(4+b+3b)=(2+2b)r,
2
1 3b2
又因为S = bcsinA= ×sinA,
2 2
3b2sin A 3 b2
所以r = , 所以Rr = × ,
4(1+b) 2 1+b
b+3b>4
由 ,解得13b
令 f(b)=
3b2
(10,
2(1+b) 2 ( 1+b )2
3
则 f(b)在(1,2)上单调递增, 所以 < f(b)<2,
4
3
故rR的取值范围为 ,2.
4
1
18. 设函数 f ( x )=lnx,g ( x )=1− ( x>0 ) .
x
( )
(1)求 f x 在x=1处的切线方程;
(2)证明: f
(
x
)≥
g
(
x
)
:
(3)若方程af ( x )= g ( x ) 有两个实根,求实数a的取值范围,
【答案】(1)x− y−1=0
(2)证明见解析 (3)(0,1)∪(1,+∞)
【解析】
【分析】(1)根据切点和斜率求得切线方程.
(2)利用构造函数法,结合导数证得不等式成立.
第15页/共19页
学科网(北京)股份有限公司(3)利用构造函数法,结合导数以及对a进行分类讨论来求得a的取值范围.
【小问1详解】
1
f′(x)= ,则k = f′(1)=1, f(1)=0.
x
∴ f(x)在x=1处的切线方程为y=x−1,即x− y−1=0.
【小问2详解】
1
令h(x)= f(x)−g(x)=lnx+ −1,x∈(0,+∞)
x
1 1 x−1
h′(x)= − = .
x x2 x2
x−1
令h′(x)= =0,解得x=1.
x2
∴0< x<1,h′(x)<0;x>1,h′(x)>0.
h(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
h(x)≥h(1)=0,即 f(x)≥ g(x).
【小问3详解】
1
令m(x)= f(x)−g(x)=alnx+ −1,x∈(0,+∞),
x
问题转化为m(x)在(0,+∞)上有两个零点.
a 1 ax−1
m′(x)= − = .
x x2 x2
①当a≤0时,
m′(x)<0,m(x)在(0,+∞)递减,m(x)至多只有一个零点,不符合要求.
②当a>0时,
1
令m′(x)=0,解得x=
a
1
当0< x< 时,m′(x)<0,m(x)递减;
a
1
当x> 时,m′(x)>0,m(x)递增.
a
1 1
所以m(x)≥m
=aln +a−1=a−alna−1.
a a
第16页/共19页
学科网(北京)股份有限公司1
当a =1时,m =m(1)=0,m(x)只有一个零点,不合题意.
a
令ϕ(a)=a−alna−1,ϕ′(a)=−lna,
当00,
所以φ(a)在(0,1)递增,ϕ(a)<ϕ(1)=0.
1 1 1 1 1
由于m(1)=0,m
=φ(a)<0,m(ea)=alnea +
1
−1=
1
>0,
a
ea ea
1 1
∴∃x ∈ ,ea ,使得m(x )=0,
1 a 1
故01时,ϕ′(a)=−lna<0,
所以φ(a)在(1,+∞)递减,φ(a)<φ(1)=0.
1 1
由于m(1)=0,m =φ(a)<0,m(e−a)=alne−a + −1=ea −a2 −1>0
a e−a
1
∴∃x ∈ e−a, ,使得m(x )=0,
2 a 2
故a>1满足条件.
综上所述:实数a的取值范围为(0,1)∪(1,+∞).
【点睛】关键点点睛:本题的解题过程中,需通过导数分析函数的性质,并将问题转化为函数零点的讨
论,充分体现了数学思想方法的应用.在解题时,要特别注意导数符号的变化对函数单调性的影响,确保
分类讨论的全面性和严谨性.
19. 如果定义域为 [ 0,1 ] 的函数 f ( x ) 同时满足以下三个条件:(1)对任意的x∈[ 0,1 ] ,总有 f(x)≥0;
(2) f ( 1 )=1;(3)当x ≥0,x ≥0,且x +x ≤1时, f ( x + x )≥ f ( x )+ f ( x ) 恒成立.则称
1 2 1 2 1 2 1 2
( )
f x 为“友谊函数”.请解答下列问题:
( ) ( )
(1)已知 f x 为“友谊函数”,求 f 0 的值;
(2)判断函数g ( x )=3x −x−1 ( x∈[ 0,1 ]) 是否为“友谊函数”?并说明理由;
(3)已知 f ( x ) 为“友谊函数”,存在x ∈[ 0,1 ] ,使得 f ( x )∈[ 0,1 ] ,且 f ( f ( x )) = x ,证明:
0 0 0 0
第17页/共19页
学科网(北京)股份有限公司f
(
x
)=
x .
0 0
【答案】(1) f ( 0 ) =0
(2)是,理由见解析.
(3)证明见解析.
【解析】
【分析】(1)结合条件,利用“赋值法”可求函数值.
(2)根据给出的条件,逐一验证即可.
(3)先判断函数的单调性,结合反证法进行证明.
【小问1详解】
由条件(1)可知: f
(
0
)≥0;
结合条件(3),令x = x =0,则 f ( 0 )≥2f ( 0 )⇒ f ( 0 )≤0.
1 2
所以: f
(
0
)=0.
【小问2详解】
函数g ( x )=3x −x−1 ( x∈[ 0,1 ]) 是“友谊函数”.理由如下:
对条件(1):因为g
(
0
)=0,g′(
x
)=3xln3−1,当x∈[
0,1
] 时,g′(
x
)>0,所以g (
x
)
在 上单调
[0,1]
递增,所以g
(
x
)≥0,x∈[
0,1
]
.
对条件(2):g
(
1
)=3−1−1=1.
对条件(3):设x ≥0,x ≥0,且x +x ≤1,则:
1 2 1 2
g ( x 1 +x 2 )− g ( x 1 )+g ( x 2 ) = 3x 1 +x 2 −( x 1 +x 2 )−1 − ( 3x 1 −x 1 −1 ) − ( 3x 2 −x 2 −1 ) =3x 1 +x 2 −3x 1 −3x 2 +1
( )( )
= 3x 1 −1 3x 2 −1 ≥0.
所以:g ( x +x )≥ g ( x )+g ( x ) .
1 2 1 2
综上可知:函数g ( x )=3x −x−1 ( x∈[ 0,1 ]) 是“友谊函数”.
【小问3详解】
设0≤ x < x ≤1且x +x ≤1,则x −x >0,
1 2 1 2 2 1
所以 f ( x )− f ( x )= f
x +( x −x )
− f ( x ) ≥ f ( x )+ f ( x −x )− f ( x ) = f ( x −x ) ≥0
2 1 1 2 1 1 1 2 1 1 2 1
第18页/共19页
学科网(北京)股份有限公司( )
所以函数 f x 在 上单调递增.
[0,1]
下面用反证法证明: f
(
x
)=
x .
0 0
假设 f
(
x
)≠
x ,则 f
(
x
)>
x 或 f
(
x
)<
x .
0 0 0 0 0 0
若 f ( x )> x ,则 f ( x )< f
f ( x )
= x ,这与 f ( x )> x 矛盾;
0 0 0 0 0 0 0
若 f ( x )< x ,则 f ( x )> f
f ( x )
= x ,这与 f ( x )< x 矛盾.
0 0 0 0 0 0 0
故假设不成立,所以 f
(
x
)=
x .
0 0
【点睛】方法点睛:对于抽象函数的问题,“赋值法”是解决问题的突破口.合理赋值是解决问题的突破
口.
第19页/共19页
学科网(北京)股份有限公司