重庆市南开中学校2023-2024学年高三下学期第七次质量检测数学试题+答4(1)_2024年3月_013月合集_2024届重庆市南开中学高三下学期第七次质量检测

重庆市高 2024 届高三第七次质量检测 数学试题 2024.3 命审单位：重庆南开中学 注意事项： 1.本试卷满分 150分，考试时间 120分钟。 2.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。 3.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改 动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本 试卷上无效。 4.考试结束后，将本试卷和答题卡一并交回。 一、单项选择题：本题共 8小题，每小题 5分，共 40分.在每小题给出的四个选项中，只有一项 符合题目要求. 1.已知随机变量X 服从正态分布N  2,2 ，P(X 1)0.7，则P(2 X 3)（ ） A.0.7 B.0.6 C.0.4 D.0.2 uuur 2.已知平面直角坐标系内两点A1,2，B2,3，则过点A且以AB为法向量的直线l的方程为（ ） A.3x y10 B.3x y20 C.3x y50 D.3yx50  1 3.若函数 f cosxcosxcos2x，则 f  f   （ ）  2 A.2 B.1 C.1 D.2 4.输血是外伤人员救治的重要手段，血液质量对提高救治成功率极为关键.血液质量的主要评判指标是血液中 ATP含量.已知血液中ATP浓度S （单位：mol/gHb）随温度（单位：℃）、时间t（单位：天）、及起 始浓度S 变化的近似函数关系式为：S S t1.08e1.30（e为自然底数，e2.71828）.由此可知，当血液在 0 0 20℃恒温条件下，保存5天后的ATP浓度，大约相当于血液在4℃恒温条件下保存（ ）天后的ATP浓度. （参考数据：ln51.6） A.16 B.20 C.25 D.30 5.已知x1(x2)n展开式中x2项的系数为48，则n（ ） A.4 B.5 C.6 D.7 6.正弦波是频率成分非常单一的信号，其波形是数学上的正弦曲线，任何复杂信号，如光谱信号，声音信号等， 都可由多个不同的正弦波复合而成.现已知某复合信号Ix由三个振幅、频率相同的正弦波 f x，gx， hx叠 加 而 成 ， 即 Ix f xgxhx . 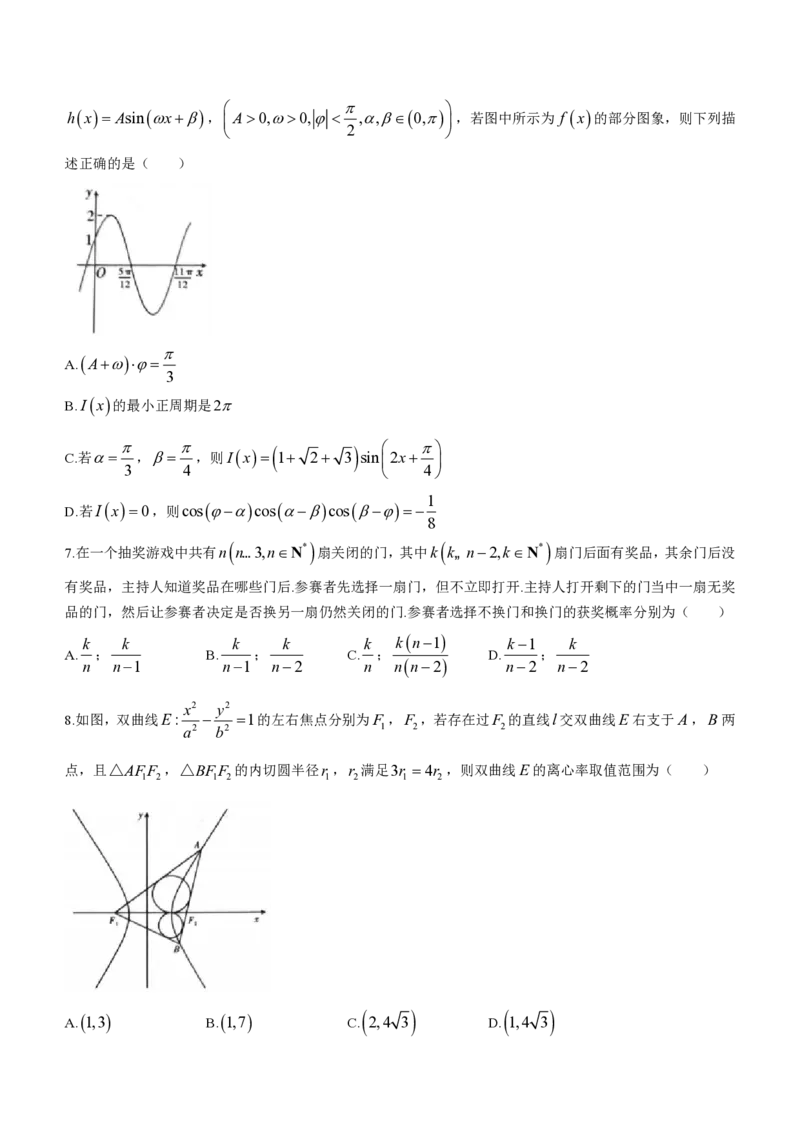设 f x Asinx， gx Asinx， 学科网（北京）股份有限公司   hx Asinx， A0,0, ,,0, ，若图中所示为 f x的部分图象，则下列描  2  述正确的是（ ）  A. A 3 B.Ix的最小正周期是2       C.若 ， ，则Ix 1 2 3 sin  2x  3 4  4  1 D.若Ix0，则coscoscos 8 7.在一个抽奖游戏中共有n  n…3,nN* 扇关闭的门，其中k  k„ n2,kN* 扇门后面有奖品，其余门后没 有奖品，主持人知道奖品在哪些门后.参赛者先选择一扇门，但不立即打开.主持人打开剩下的门当中一扇无奖 品的门，然后让参赛者决定是否换另一扇仍然关闭的门.参赛者选择不换门和换门的获奖概率分别为（ ） k k k k k kn1 k1 k A. ； B. ； C. ； D. 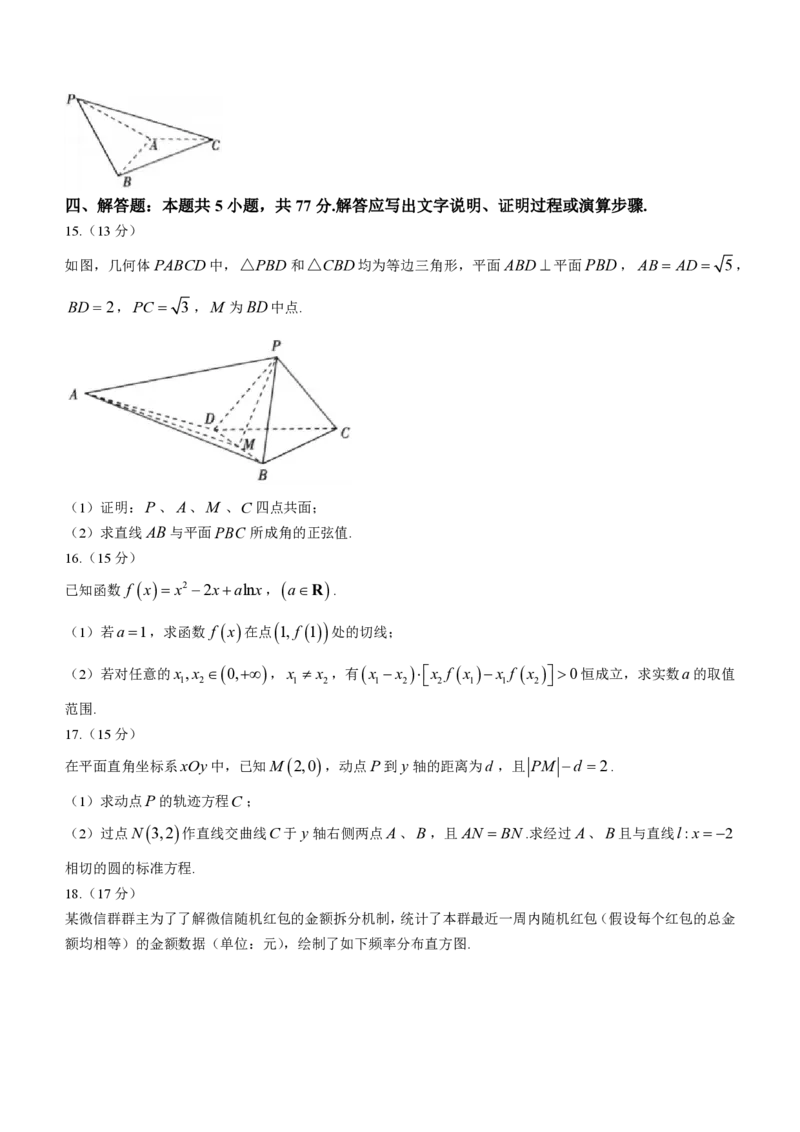； n n1 n1 n2 n nn2 n2 n2 x2 y2 8.如图，双曲线E:  1的左右焦点分别为F ，F ，若存在过F 的直线l交双曲线E右支于A，B两 a2 b2 1 2 2 点，且△AFF ，△BFF 的内切圆半径r ，r 满足3r 4r ，则双曲线E的离心率取值范围为（ ） 1 2 1 2 1 2 1 2     A. 1,3 B. 1,7 C. 2,4 3 D. 1,4 3 学科网（北京）股份有限公司二、选择题：本题共 3小题，每小题 6分，共 18分.在每小题给出的选项中，有多项符合题目要 求.全部选对的得 6分，部分选对的得部分分，有选错的得 0分. 9.下列命题中正确的是（ ） r r r r r r r r A.若向量a，b 满足 ab  a b ，则aPb r r r r r r r r B.若非零向量a，b 满足 ab  ab ，则a b r r r r r r r r r C.若a，b ，c为平面向量，则 ab c a bc r r r r r r r r r D.若a，b ，c为非零向量，且满足ab ac ，则b c x 1 10.已知函数 f x ， f 11， f 33，令x  ，x  f x  .则（ ） axb 1 3 n1 n  1  A.a1，b  2 B.数列 为等差数列 x   n n C. x 1 D. x 1x 1x 1L x 1e i 1 2 3 n i1 1 11. 已 知 三 次 函 数 f xax3 x2 cx 有 三 个 不 同 的 零 点 x ,x ,x x  x  x ， 函 数 27 1 2 3 1 2 3 gx f x1.则（ ） A.3ac1 B.若x ，x ，x 成等差数列，则a1,0U0,1 1 2 3 1 C.若gx恰有两个不同的零点m,n(mn)，则2mn 3a D.若gx有三个不同的零点t ,t ,t t t t ，则x2 x2 x2 t2 t2 t2 1 2 3 1 2 3 1 2 3 1 2 3 三、填空题：本题共 3小题，每小题 5分，共 15分. 1 3i 12.已知复数 ，则2024 ________. 2 13. 已 知 △ABC的 内 角 A， B， C所 对 应 的 边 分 别 是 a， b， c，  10  cosAcosBcosAcosBsinC  sinC sinA ， b3 2， ac6， 则 △ABC的 面 积 为  13  ________. 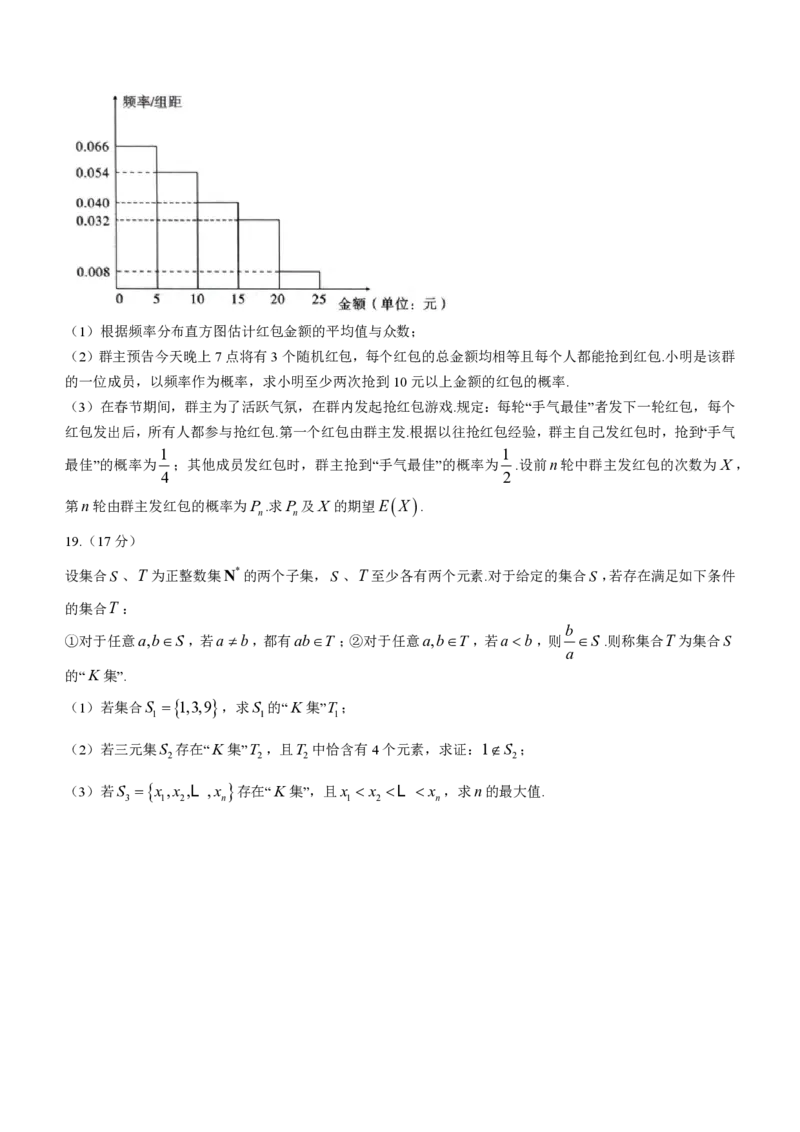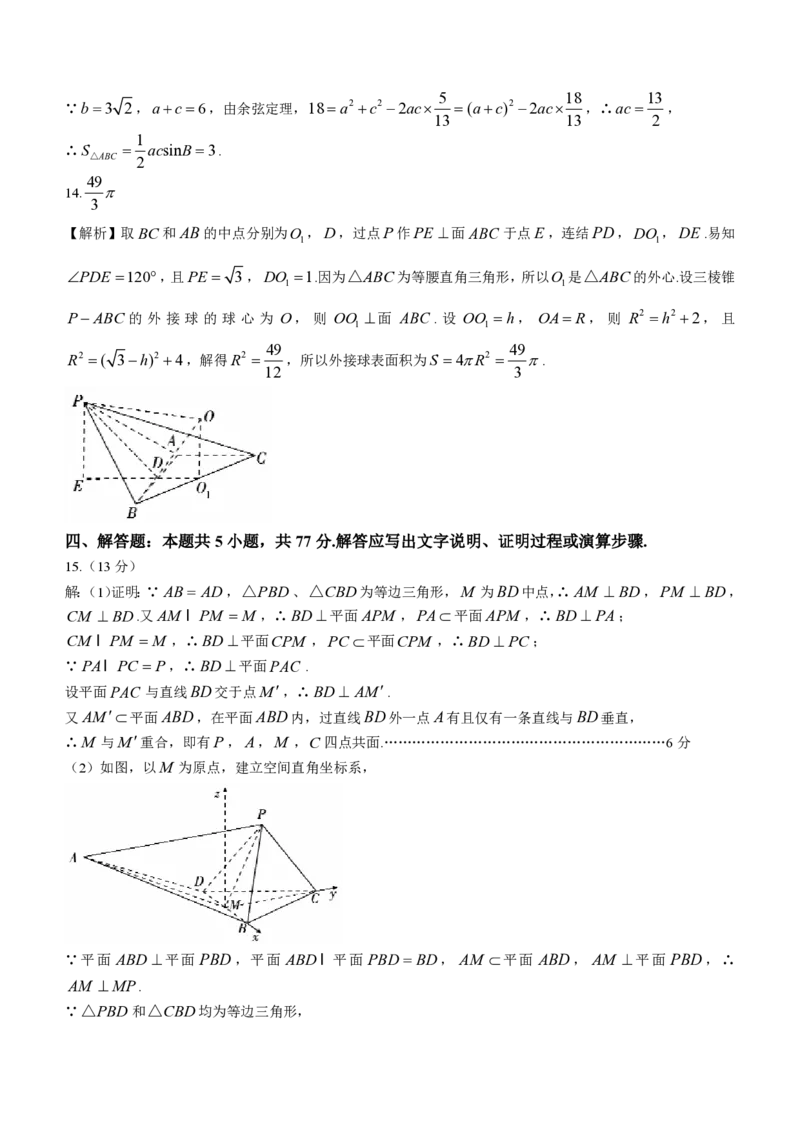14.如图，在三棱锥PABC 中，PA PB 5，CA AB，AB AC 2，二面角PABC的大小为 120，则三棱锥PABC 的外接球表面积为________. 学科网（北京）股份有限公司四、解答题：本题共 5小题，共 77分.解答应写出文字说明、证明过程或演算步骤. 15.（13分） 如图，几何体PABCD中，△PBD和△CBD均为等边三角形，平面ABD平面PBD，AB AD 5， BD2，PC  3，M 为BD中点. （1）证明：P、A、M 、C四点共面； （2）求直线AB与平面PBC 所成角的正弦值. 16.（15分） 已知函数 f x x2 2xalnx，aR . （1）若a1，求函数 f x在点  1, f 1 处的切线； （2）若对任意的x ,x 0,，x  x ，有x x x f x x f x  0恒成立，求实数a的取值 1 2 1 2 1 2  2 1 1 2  范围. 17.（15分） 在平面直角坐标系xOy中，已知M 2,0，动点P到y轴的距离为d ，且 PM d 2. （1）求动点P的轨迹方程C； （2）过点N3,2作直线交曲线C于y轴右侧两点A、B，且AN  BN.求经过A、B且与直线l:x2 相切的圆的标准方程. 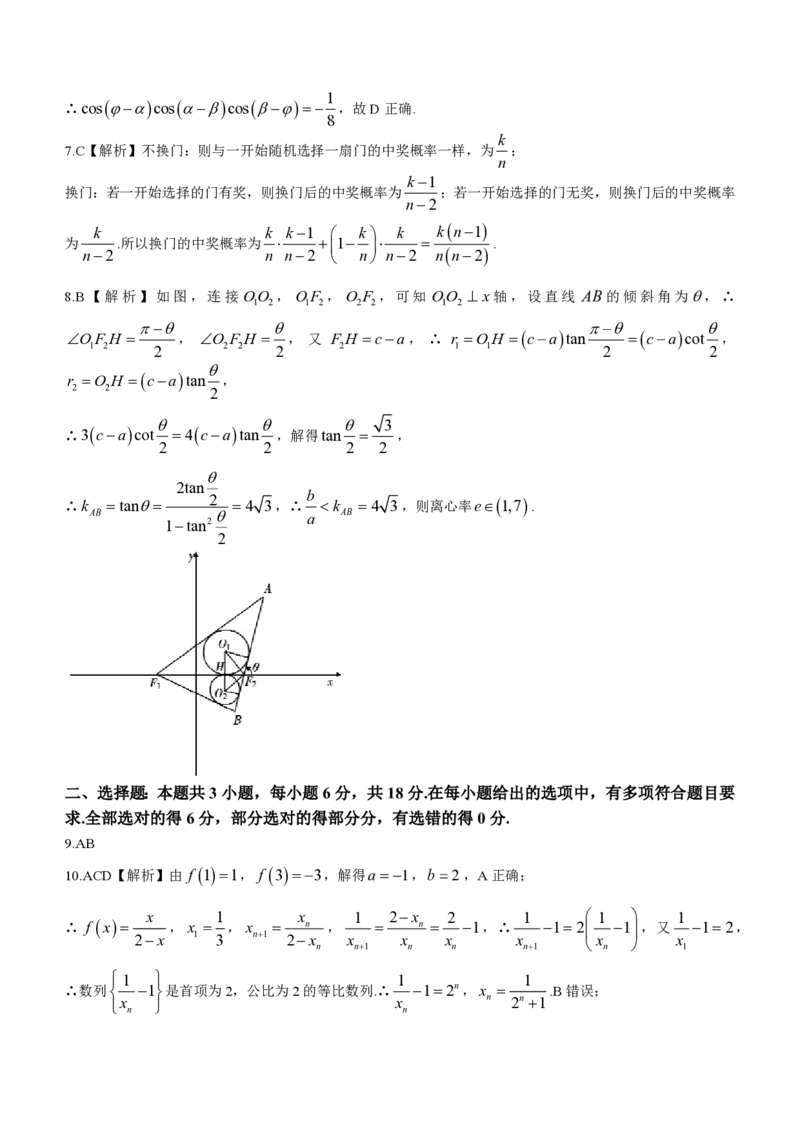18.（17分） 某微信群群主为了了解微信随机红包的金额拆分机制，统计了本群最近一周内随机红包（假设每个红包的总金 额均相等）的金额数据（单位：元），绘制了如下频率分布直方图. 学科网（北京）股份有限公司（1）根据频率分布直方图估计红包金额的平均值与众数； （2）群主预告今天晚上7点将有3个随机红包，每个红包的总金额均相等且每个人都能抢到红包.小明是该群 的一位成员，以频率作为概率，求小明至少两次抢到10元以上金额的红包的概率. （3）在春节期间，群主为了活跃气氛，在群内发起抢红包游戏.规定：每轮“手气最佳”者发下一轮红包，每个 红包发出后，所有人都参与抢红包.第一个红包由群主发.根据以往抢红包经验，群主自己发红包时，抢到“手气 1 1 最佳”的概率为 ；其他成员发红包时，群主抢到“手气最佳”的概率为 .设前n轮中群主发红包的次数为X ， 4 2 第n轮由群主发红包的概率为P .求P 及X 的期望EX . n n 19.（17分） 设集合S 、T 为正整数集N*的两个子集，S 、T 至少各有两个元素.对于给定的集合S ，若存在满足如下条件 的集合T ： b ①对于任意a,bS ，若a b，都有abT ；②对于任意a,bT ，若a b，则 S .则称集合T 为集合S a 的“K集”. （1）若集合S 1,3,9，求S 的“K集”T ； 1 1 1 （2）若三元集S 存在“K集”T ，且T 中恰含有4个元素，求证：1S ； 2 2 2 2 （3）若S x ,x ,L ,x 存在“K集”，且x  x L  x ，求n的最大值. 3 1 2 n 1 2 n 学科网（北京）股份有限公司重庆市高 2024 届高三第七次质量检测 数学试题参考答案与评分细则 题号 1 2 3 4 5 6 7 8 9 10 11 选项 D A B C C D C B AB ACD ABD 一、单项选择题：本题共 8小题.每小题 5分，共 40分. 1.D【解析】因为P(X 1)0.7，∴P(X 3) P(X 1)0.3，∴P(2 X 3)0.2. 1 2.A【解析】k  ，所以直线l的斜率为k 3，所以直线方程为y 3x123x1. AB 3 l 1 1 1 3.B【解析】 f x x2x2 1， f    2 10， f 01. 2 2 4 521.6 4.C【解析】设所求为t天，代入数据得：S 51.0820e1.3020 S t1.084e1.304，解得t4.32  ，取对数为 0 0 e20.8 21.6ln520.8 lnt  3.22ln5，所以t 25. 4.32 5.C【解析】由题意有C12n1C22n2 48，带入选项，n 6满足题意. n n 11 5  1  6.D【解析】由图可知，A2，且    T  ，所以2. 12 12 2 2  1   2 又 f 01，所以sin .因为 ，所以 .所以A ，A错误. 2 2 6 3 因为2，所以 f x，gx，hx的最小正周期均为，所以Ix f xgxhx的最小正周 期为，B选项错误.   因 为  ，  ， 所 以 3 4           Ix2sin  2x  2sin  2x  2sin  2x   22 6 sin  2x ，C错误.  6   3   4   4  因 为 Ix0， 所 以 2sin2x2sin2x2sin2x0， 展 开 得 coscoscos0 sin2xcoscoscoscos2xsinsinsin0，等式恒成立，则 ， sinsinsin0 coscoscos 1 ∴  ，平方求和得： 22cos1，∴ cos ；同理，可得 sinsinsin 2 1 1 cos ，cos ， 2 2 学科网（北京）股份有限公司1 ∴coscoscos ，故D正确. 8 k 7.C【解析】不换门：则与一开始随机选择一扇门的中奖概率一样，为 ； n k1 换门：若一开始选择的门有奖，则换门后的中奖概率为 ；若一开始选择的门无奖，则换门后的中奖概率 n2 k k k1  k  k kn1 为 .所以换门的中奖概率为    1    . n2 n n2  n n2 nn2 8.B【解析】如图，连接 OO ， OF ， O F ，可知 OO  x轴，设直线 AB的倾斜角为，∴ 1 2 1 2 2 2 1 2     OF H  ， O F H  ， 又 F H ca， ∴ r OH catan cacot ， 1 2 2 2 2 2 2 1 1 2 2  r O H catan ， 2 2 2    3 ∴3cacot 4catan ，解得tan  ， 2 2 2 2  2tan b ∴k tan 2 4 3，∴ k 4 3，则离心率e1,7 . AB  a AB 1tan2 2 二、选择题：本题共 3小题，每小题 6分，共 18分.在每小题给出的选项中，有多项符合题目要 求.全部选对的得 6分，部分选对的得部分分，有选错的得 0分. 9.AB 10.ACD【解析】由 f 11， f 33，解得a1，b  2，A正确； x 1 x 1 2x 2 1  1  1 ∴ f x ， x  ， x  n ，  n  1，∴ 12 1，又 12， 2x 1 3 n1 2x x x x x x x   n n1 n n n1 n 1  1  1 1 ∴数列 1是首项为2，公比为2的等比数列.∴ 12n，x  .B错误； x x n 2n 1   n n 学科网（北京）股份有限公司n 1 1 1 1 1 1 1 ∴x   L    L  1 1.C正确； i 211 22 1 2n 1 21 22 2n 2n i1 lnx 1x 1x 1L x 1lnx 1lnx 1L lnx 1 x x L x 1， 即 1 2 3 n 1 2 n 1 2 n x 1x 1x 1L x 1e.D正确. 1 2 3 n 1 11.ABD 【 解 析 】 f xax3 x2 cx ， fx3ax2 2xc， a  0， 对 称 中 心 为 27  1  1    , f   ，对 A：因为 f x有三个零点，所以 f x必有两个极值点，所以Δ412ac0，  3a  3a 3ac1，A正确； 1 对B，由x ，x ，x 成等差数列，及三次函数的中心对称性可知x  ， 1 2 3 2 3a  1  2a2 9ac 1 所 以 f x  f     0， 又 ac ， 故 2a2 9ac3， 所 以 a2 1， 所 以 2  3a 27a2 3 a1,0U0,1，故B正确； 26 对C：gx0，即ax3x2 cx 0，若gx恰有两个零点，则m或n必为极值点； 27 1 若m为极值点，则该方程的三个根为m，m，n，由一元三次方程的韦达定理可知：2mn ； a 1 若n为极值点，同理可得m2n ，故C错； a  1 x x x t t t    1 2 3 1 2 3 a 对D：由韦达定理 c  x x x x x x tt t t t t   1 2 2 3 3 1 1 2 2 3 31 a 得x x x 2 2x x x x x x t t t 2 2tt t t t t ，即x2 x2 x2 t2 t2 t2， 1 2 3 1 2 2 3 3 1 1 2 3 1 2 2 3 31 1 2 3 1 2 3 故D正确. 三、填空题：本题共 3小题，每小题 5分，共 15分. 1 3i 12. 2 1 3i 1 3i 1 3i 【解析】∵ ，∴2  ，3 1，∴2024 20222  . 2 2 2 13.3  10  5 12 【解析】∵cosAcosBcosAcosBsinC  sinC sinA ，∴cosB ，sinB .  13  13 13 学科网（北京）股份有限公司5 18 13 ∵b3 2，ac6，由余弦定理，18a2 c2 2ac (ac)2 2ac ，∴ac ， 13 13 2 1 ∴S  acsinB3. △ABC 2 49 14.  3 【解析】取BC和AB的中点分别为O ，D，过点P作PE 面ABC 于点E，连结PD，DO ，DE.易知 1 1 PDE 120，且PE  3，DO 1.因为△ABC为等腰直角三角形，所以O 是△ABC的外心.设三棱锥 1 1 PABC 的 外 接 球 的 球 心 为 O， 则 OO 面 ABC . 设 OO h， OA R， 则 R2 h2 2， 且 1 1 49 49 R2 ( 3h)2 4，解得R2  ，所以外接球表面积为S 4R2  . 12 3 四、解答题：本题共 5小题，共 77分.解答应写出文字说明、证明过程或演算步骤. 15.（13分） 解：（1）证明：∵AB AD，△PBD、△CBD为等边三角形，M 为BD中点，∴AM  BD，PM  BD， CM  BD.又AM I PM M ，∴BD平面APM ，PA平面APM ，∴BD PA； CM I PM M ，∴BD平面CPM ，PC 平面CPM ，∴BD PC； ∵PAI PC  P，∴BD平面PAC . 设平面PAC 与直线BD交于点M，∴BD AM. 又AM平面ABD，在平面ABD内，过直线BD外一点A有且仅有一条直线与BD垂直， ∴M 与M重合，即有P，A，M ，C四点共面.……………………………………………………6分 （2）如图，以M 为原点，建立空间直角坐标系， ∵平面 ABD平面 PBD，平面 ABDI 平面 PBD BD， AM 平面 ABD， AM 平面 PBD，∴ AM MP. ∵△PBD和△CBD均为等边三角形， 学科网（北京）股份有限公司∴PM MC  PC  3，PMC 60.  3 3     ∴P0, , ，C 0, 3,0 ，B1,0,0，A 0, 3,1 .   2 2   uuur   uuur  3 3 uuur   ∴AB 1, 3,1 ，BP1, , ，BC  1, 3,0 .   2 2   uuur uuur r r 3 3 r 设平面PBC 的法向量为mx,y,z，∴mBPx y z 0，mBC x 3y 0. 2 2 r   取m 3, 3,1 . uuur ur 5 65 设直线AB与平面PBC 夹角为，∴sin cos AB,m   . 5 13 13 65 ∴直线AB与平面PBC 所成角的正弦值为 .…………………………………………15分 13 16.（15分） a 解：（1） fx2x2 ，当a1，时， f 11， fx1，故切线方程为：y  x2；……5分 x f x  f x  （2）法一：不妨设0 x  x ，则x f x x f x 0，同除以x x 得 1  2 ， 1 2 2 1 1 2 1 2 x x 1 2 f x alnx a1lnx 所以Gx  x2 在0,单调递增，所以Gx1 …0.……7分 x x x2 ①若a 0，Gx0恒成立，符合题意. 1 lnx1 lnx1 32lnx  3  ②若a 0，则 … 恒成立.令Fx ，则Fx ，所以Fx在0,e2 单调递增， a x2 x2 x3    3  1  3  1 在e2,单调递减，所以 …Fe2  ，所以a  0,2e3  . a 2e3     1 lnx1 ③若a 0，同理， „ 恒成立，由②可知，当x0时，Fx，所以不存在满足条件的a. a x2 综上所述，a0,2e3.……………………………………………………………………15分    f x  f x  法二：x 1 x 2   x 2 f x 1 x 1 f x 2   0x 1 x 2  x 1  x 2  0，   1 2 学科网（北京）股份有限公司f x lnx 令gx  x2a ，则只需gx在0,单调递增，即gx…0恒成立；……7分 x x a1lnx x2 a1lnx gx1  ， x2 x2 a 2x2 a 令hx x2 a1lnx，则hx…0恒成立；又hx2x  ， x x ①当a 0时，hx x2，hx在0,单调递增成立； ②当a 0时，hx0，hx在0,单调递增， 又当x0时，hx，故hx…0不恒成立，不满足题意； a  a   a  （3）当a 0时，由hx0得x ，则hx在0, 单调递减，在 ,单调递增，     2 2 2      a  a  a  a a 因为hx…0恒成立，所以h(x) min h   2     2 a   1ln 2     2   3ln 2   …0， 解得a„ 2e3，故0a„ 2e3； 综上，实数a的取值范围是a0,2e3.…………………………………………15分   17.（15分） 解：（1）M 2,0，设Px,y，因为 PM d 2，所以 (x2)2  y2  x 2， 整理得y2 4 x 4x，所以，当x…0时，y2 8x；当x 0时，y 0； 所以P的轨迹方程为C：y2 8xx…0，y 0(x0).……………………………………6分 （2）过 N3,2的直线不与 x轴的负半轴相交， N 为 AB中点，设 Ax ,y ， Bx ,y ，联立 1 1 2 2 y2 8x y2  y2 y  y y  y  1 1  1 2 8，即 1 2 1 2 4，∴2k 4，k 2.∴直线AB：y 2x4. y2 8x x x 2 x x AB AB  2 2 1 2 1 2 y2 8x 此时l：x2为抛物线的准线，M 2,0为焦点，联立  y2 4y160 y 2x4 由韦达定理可得y  y 4，y y 16，得弦长 AB 10， 1 2 1 2 1 7 所以直线AB的中垂线的方程为：y  x ， 2 2 学科网（北京）股份有限公司 7m 由圆心在弦的中垂线上，故可设圆心为Q  m, ，半径为R，  2  因为圆Q与直线l相切，故R m2  m2 ， 又R2  QA|2 QN |2  AN |2 QN |2  | AB|2 (m3)2  7m 2  2 25 1  5m2 30m145  ，   4  2  4 1 所以|m2|2  5m2 30m145  ，即m2 46m1290，解得m3或m43； 4 故Q3,2或Q43,18，半径R5或45， 故圆Q的方程为：(x3)2 (y2)2 25或(x43)2 (y18)2 2025.…………15分 18.（17分） 5 15 25 35 45 解：（1）平均值为：x0.0665 0.0545 0.0405 0.0325 0.0085 9.05； 2 2 2 2 2 众数为最高矩形的中点坐标，即为2.5.………………………………………………3分 （2）由题可知，每个红包抢到10元以上金额的概率为0.4，且3次红包相互独立，所以至少两次抢到10元以 44 上金额的概率为C20.420.6C30.43 0.352 ；………………8分 3 3 125 1 1 （3）由题意，P 1，P  P  1P ， 1 n1 4 n 2 n 2 1 2 2 3 ∴P    P  ，又P   ， n1 5 4 n 5 1 5 5 n1  2 3 1 2 3  1 ∴P  是以 为首项， 为公比的等比数列，∴P       .  n 5 5 4 n 5 5  4 n1 2 3  1 ∴P       .……………………………………………………13分 n 5 5  4 设为第k轮发红包时群主抢到“手气最佳”的次数， k 故服从两点分布：P 1 P ，P 01P . k 1,2,3L ， k k k k k ∴E1P 01P  P . k k k k 由已知X   L ，则 1 2 3 n EX E  L  1 2 3 n  EEEL E 1 2 3 n 学科网（北京）股份有限公司 P P P L P 1 2 3 n n  1 1    2n 3  4    5 5 1 1 4 2n 12   1 n   1    ………………………………………………………………17分 5 25   4  19.（17分） 9 27 27 解：（1）若S 1,3,9，由题意可得，13，19，39T ，即3,9,27T ，此时 , , S ，满足 1 3 3 9 1 题意， 27 27 假设集合T 中还有第四个元素为t，则由题意可知：若t 3，即 9，则 S ，∴不成立； t t 1 t 若t 3，则 S ，∴t 3或9或27，矛盾.故集合T 中无四个元素，所以集合T 3,9,27 .……3分 3 1 （2）设集合S a ,a ,a ，不妨设a a a ， 2 1 2 3 1 2 3 假设1S ，即a 1，则1a a 且a ,a ,a a T ， 2 1 2 3 2 3 2 3 a a a 由②知 3 S ，注意到1 3 a ，故有 3 a ，即a a2，所以S   1,a ,a2 ， a 2 a 3 a 2 3 2 2 2 2 2 2 2 故a a a3T ，即a ,a2,a3T ，因为集合T 中有4个元素，故设T   a ,a2,a3,t  ， 2 3 2 2 2 2 2 2 2 a3 a3 由②可得：若t a ，则 2 a2，∴ 2 S ，矛盾； 2 t 2 t 2 t t 若t a ， S ，则 1或a 或a2，所以t a 或a2或a3，与集合元素的互异性矛盾， 2 a 2 a 2 2 2 2 2 2 2 假设错误，故1S .……………………………………………………………………9分 2 （3）S x ,x ,L ,x N*，x ,x ,L ,x N*，不妨设1„ x  x L  x ， 3 1 2 n 1 2 n 1 2 n x x x x 所以x x T ，x x T ，又x x  x x ，故 2 n  n S ，同理可得 j S (1„ i j„ n)， 1 2 2 n 1 2 2 n x x x 3 x 3 1 2 1 i 若x 1，与（2）类似得S   1,x ,x2,L ,xn1 ，从而必有x ,x2,L x2n3T ， 1 3 2 2 2 2 2 2 xj 对任意的1„ i j„ 2n3，有xji  2 S ，即x1,x2,L x2n4S ，所以2n4„ n1，即n„ 3. 2 xi 3 2 2 2 3 2 学科网（北京）股份有限公司x x x x x x x 若x 1，即x…2，1 2  3L  n  x ，故 n  x ， n1  x ，L 3  x ， 2  x ， 1 1 x x x n x n1 x n2 x 2 x 1 1 1 1 1 1 1 1 所以x  x2,x  x3,L ,x  xn1,x  xn，即S   x ,x2,L ,xn ，从而必有x3,x4,L ,x2n1T ， 2 1 3 1 n1 1 n 1 3 1 1 1 1 1 1 xj 对任意的3„ i j„ 2n1，必有xji  1 S ，即x1,x2,L x2n4S ，所以2n4„ n，即n„ 4. 1 xi 3 2 2 2 3 1 综上，得n„ 4，又n  4时，有S 2,4,8,16，T 8,16,32,64,128符合题意， 所以n的最大值为4.………………………………………………………………17分 学科网（北京）股份有限公司