文档内容
2023 级高二年级考试
数学试卷
试卷满分:150 考试时间:150 分钟
一、单项选择题
1. 5 位同学报名参加两个课外活动小组,每位同学限报其中的一个小组,则不同报名方法有( )
A. 10 种 B. 20 种 C. 25 种 D. 32 种
【答案】D
【解析】
【分析】由分步乘法原理计算.
【详解】由题意,每个同学有 2 种选择,故不同报名方式为 .
故选:D
2. 下列说法中,错误的命题是( )
A. 在刻画回归模型的拟合效果时, 的值越大,说明拟合的效果越好
B. 线性相关系数 越大,两个变量的线性相关性越强,反之,线性相关性越弱
C. 设随机变量 服从正态分布 ,则
D. 对分类变量 与 ,若计算出的 越大,则判断“ 与 有关系”的犯错误的概率越小
【答案】B
【解析】
【分析】由 的值与回归模型的关系可判断 A 选项;由相关系数的概念可判断 B,利用正态分布密度曲线
的对称性可判断 C 选项;利用独立型检验可判断 D 选项.
【详解】对于 A:在刻画回归模型的拟合效果时, 的值越大,说明拟合的效果越好,正确;
对于 B:线性相关系数 越大,两个变量的线性相关性越强,反之,线性相关性越弱,错误;
对于 C:由正太密度曲线的对称性可知: ,正确;
对于 D:对分类变量 与 ,若计算出的 越大,则判断“ 与 有关系”的犯错误的概率越小,正确.
故选:B
3. 某班要从 8 名班干部(其中 5 名男生,3 名女生)中选取 3 人参加学校优秀班干部评选,事件 :男生
甲被选中,事件 :有两名女生被选中,则 为( )
第 1页/共 18页A. B. C. D.
【答案】B
【解析】
【分析】计算出事件 、 的概率,利用条件概率公式可求得 的值.
【详解】由题意可得 ,
事件 男生甲与两名女生被选中,则 ,
因此, .
故选:B.
4. 已知 ,则 为( )
A. 180 B. 150 C. 120 D. 200
【答案】A
【解析】
【分析】由 ,结合通项公式即可求解.
【详解】因 ,
其通项公式为: ,
令 ,可得: .
故选:A
5. 从 5 位同学中选派 4 位同学在星期五、星期六、星期日参加公益活动,每人一天,要求星期五有 2 人参
加,星期六、星期日各有 1 人参加,则不同的选派方法共有
A. 40 种 B. 60 种 C. 100 种 D. 120 种
【答案】B
【解析】
【详解】根据题意,首先从 5 人中抽出两人在星期五参加活动,有 种情况,
第 2页/共 18页再从剩下的 3 人中,抽取两人安排在星期六、星期日参加活动,有 种情况,
则由分步计数原理,可得不同的选派方法共有 =60 种.
故选 B.
6. 已知随机变量 的分布列如下,则 的最大值为( )
X 1 2 3
P a b 2b—a
A. B. 3
C. 6 D. 5
【答案】C
【解析】
【分析】根据概率和为 得到求得 ,根据分布列求得 ,求 的最大值,再求
的最大值即可.
【详解】因为分布列中概率和为 ,故可得 ,解得 ,
又 ,
则 ,
又 ,故可得 ,
则当 时, 的最大值为 ,
又 ,故 的最大值为 .
故选:C.
7. 从非洲蔓延到东南亚的蝗虫灾害严重威胁了国际农业生产,影响了人民生活.世界性与区域性温度的异
常、旱涝频繁发生给蝗灾发生创造了机会.已知蝗虫的产卵量 与温度 的关系可以用模型 (其
第 3页/共 18页中 为自然底数)拟合,设 ,其变换后得到一组数据:
由上表可得线性回归方程 ,则当 时,蝗虫的产卵量 的估计值为( )
A. B. C. D.
【答案】B
【解析】
【分析】先根据表中的数据求出 ,代入 中求出 的值,从而可得 ,而
,所以 ,则可求得 ,再将 代入可求得答案
【详解】由表格数据知: , ,
代入 ,得 ,
,即 ,
, 时, ,
故选:B.
8. 已知甲盒中有 2 个球且都为红球,乙盒中有 3 个红球和 4 个蓝球,从乙盒中随机抽取 个球放入
甲盒中
(1)放入 个球后,甲盒中含有红球的个数记为 ;
(2)放入 个球后,从甲盒中取 1 个球是红球的概率记为 ,则( )
A B.
C. D.
【答案】A
【解析】
【分析】求得两种情况下的 , , ,比较可得结论.
【详解】从乙盒中取 1 个球时,甲盒红球个数记为 ,则 的所有可能取值为 2,3,
第 4页/共 18页则
从乙盒中随机抽取 1 个篮球放入甲盒中的概率是 ,乙盒中随机抽取 1 个红球放入甲盒中的概率是 ,
从乙盒中取 2 个球时,甲盒红球数记为 ,则 的可能取值为 ,
,
.
故选:A.
二、多项选择题
9. 在某次数学测试中,学生 成绩 ,则( )
A. B. 若 越大,则 越大
C. D.
【答案】AC
【解析】
【分析】根据正态曲线的对称性结合选项逐个分析可得答案.
【详解】因为 ,所以 ,A 正确;
当 时, ,当 时, ,B 不正确;
因为 ,所以 ,C 正确;
根据正态曲线的对称性 ,D 不正确.
故选:AC.
10. 下列选项中正确的有( ).
A. 随机变量 ,则
B. 将两颗骰子各掷一次,设事件 “两个点数不相同”, “至少出现一个 6 点”,则概率
第 5页/共 18页C. 口袋中有 7 个红球、2 个蓝球和 1 个黑球.从中任取两个球,记其中含红球的个数为随机变量 .则 的数
学期望
D. 已知某种药物对某种疾病的治愈率为 ,现有 3 位患有该病的患者服用了这种药物,3 位患者是否会被
治愈是相互独立的,则恰有 1 位患者被治愈的概率为
【答案】AC
【解析】
【分析】对于 A,利用二项分布定义求解即可;对于 B,代入条件概率公式即可;对于 C,写出 的所有可
能取值,列出分布列计算即可;对于 D,代入 次独立重复试验中恰好发生 次的概率公式即可.
【详解】对于 A, 随机变量 服从二项分布 , .
则 ,故 A 正确;
对于 B,根据条件概率的含义, 其含义为在 发生的情况下, 发生的概率,
即在“至少出现一个 6 点”的情况下,“两个点数都不相同”的概率,
“至少出现一个 6 点”的情况数目为 ,
“两个点数都不相同”则只有一个 6 点,共 种,
故 ,故 B 错误;
对于 C, 的所有可能取值为 0,1,2,
,
可得 , , .
的分布列
0 1 2
第 6页/共 18页,故 C 正确;
对于 D,某种药物对某种疾病的治愈率为 ,现有 3 位患有该病的患者服用了这种药物,3 位患者是否会被
治愈是相互独立的,则恰有 1 位患者被治愈的概率为 ,故 D 错误.
故选:AC.
【点睛】本题考查了二项分布、条件概率、相互独立事件和相互独立事件的概率乘法公式、 次独立重复
试验中恰好发生 次的概率等,知识点较多,但难度不大,仔细分析每一个选项即可.
11. 已知红箱内有 6 个红球、3 个白球,白箱内有 3 个红球、6 个白球,所有小球大小、形状完全相同.第
一次从红箱内取出一球后再放回去,第二次从与第一次取出的球颜色相同的箱子内取出一球,然后再放回
去,依此类推,第 次从与第 k 次取出的球颜色相同的箱子内取出一球,然后再放回去.记第 次取出
的球是红球的概率为 ,则下列说法正确的是( )
A. B.
C. 第 5 次取出的球是红球的概率为 D. 前 3 次取球恰有 2 次取到红球的概率是
【答案】AC
【解析】
【分析】依题意求出 ,设第 次取出球是红球的概率为 ,则白球概率为 ,即可求出第 次取
出红球的概率,即可得到 ,从而可判断各个选项.
【详解】依题意 ,
设第 次取出球是红球的概率为 ,则白球概率为 ,
对于第 次,取出红球有两种情况.
①从红箱取出的概率为 ,②从白箱取出的概率为 ,
对应 ,即 ,故 B 错误;
所以 ,
第 7页/共 18页令 ,则数列 为等比数列,公比为 ,因为 ,所以 ,
故 ,所以 , 故选项 A,C 正确;
第 1 次取出球是红球的概率为 ,第 2 次取出球是红球的概率为 ,
第 3 次取出球是红球的概率为 ,
前 3 次取球恰有 2 次取到红球的概率是 ,
故 D 错误;
故选:AC.
三、填空题
12. 若 的二项展开式中,所有二项式系数和为 ,则该展开式中的常数项为________.
【答案】15
【解析】
【详解】试题分析:在二项展开式 中二项式系数和为 ,故 , ,展开式通项为
,要求常数项,则令 , ,因此常数项为 .
考点:二项展开式的通项与二项式系数.
13. 某学校组织学生进行答题比赛,已知共有 4 道 类试题,8 道 类试题,12 道 类试题,学生从中任选
1 道试题作答,学生甲答对 这 3 类试题的概率分别为 , , .若学生甲答对了所选试题,则这道
试题是 类试题的概率为_____________.
【答案】
【解析】
【分析】利用全概率公式及条件概率公式计算可得.
【详解】设学生选 道 类试题为事件 ,学生选 道 类试题为事件 ,学生选 道 类试题为事件 ,
设学生答对试题为事件 ,则 , , ,
, , ,
所以 ,
第 8页/共 18页所以 .
故答案为:
14. 某次大型联考 10000 名学生参加,考试成绩(满分 100 分)近似服从正态分布 (其中
和 分别为样本的均值和标准差),若本次考试平均成绩为 65 分,87 分以上共有 228 人,学生甲的成绩为
76 分,则学生甲的名次大致是__________名.
附:若随机变量 服从正态分布 ,则 ,
【答案】1587
【解析】
【分析】由本次模拟考试成绩都近似服从正态分布 , ,87 分以上共有 228 人,结合 原
则,求得 ,再由甲市学生 在该次考试中成绩为 76 分,且 ,利用概率公式求解
即得.
【详解】已知本次模拟考试成绩都近似服从正态分布 ,
由题意可得 .
,而
即 ,解得 .
甲市学生 在该次考试中成绩为 76 分,且 ,
又 ,即 .
学生 在甲市本次考试的大致名次为 1587 名.
故答案 :1587
四、解答题
15. 用 0,1,2,3,4,5 这六个数字,能组成多少个符合下列条件的数字?(运算结果以数字作答)
第 9页/共 18页(1)无重复数字的四位偶数;
(2)无重复数字且为 5 的倍数的四位数;
(3)无重复数字且比 1230 大的四位数.
【答案】(1) 个
(2) 个
(3) 个
【解析】
【分析】(1)分个位数字为 0,2,4,三种情况分别应用排列计算结合分类加法原理计算即可;
(2)分个位数字为 0,5,两种情况分别应用排列计算结合分类加法原理计算即可;
(3)分首位数字,百位数字,十位数字,个位数字比 1230 大分类讨论列排列数结合加法原理计算求解.
【小问 1 详解】
符合要求的四位偶数可分为两类.
第一类,0 在个位时有 个;
第二类,2 或 4 在个位时,首位从 1,3,4(或 2),5 中选(有 种情况),十位和百位从余下的数字中选
(有 种情况),于是有 个.
由分类加法计数原理知,共有四位偶数 (个).
【小问 2 详解】
符合要求的数可分为两类:第一类:0 在个位时有 个;
第二类:5 在个位时有 个.
故满足条件的四位数共有 (个).
【小问 3 详解】
符合要求的比 1230 大的四位数可分为四类:
第一类:形如 2□□□,3□□□,4□□□,5□□□,共有 个;
第二类:形如 13□□,14□□,15□□,共有 个;
第三类:形如 124□,125□,共有 个;
第四类:形如 123□,共有 个.
第 10页/共 18页由分类加法计数原理知,
无重复数字且比 1230 大的四位数共有 (个).
16. 已知在 的展开式中,前 3 项的系数分别为 ,且满足 .求:
(1)展开式中二项式系数最大项的项;
(2)展开式中系数最大的项;
(3)展开式中所有有理项.
【答案】(1)
(2) 和
(3) 和
【解析】
【分析】(1)由二项式展开式通项公式,结合条件列方程求 ,再由二项式系数的性质求二项式系数最大的
项;
(2)设第 项系数最大,列不等式组求 ,由此确定系数最大的项;
(3)根据有理项的定义确定有理项的项数,再求有理项.
【小问 1 详解】
因为 展开式的通项公式为 , ,
所以
依题意得 ,即 ,由已知 ,
所以 ,
所以 的展开式有 9 项,二项式系数最大的项为第 5 项,
所以 .
【小问 2 详解】
第 11页/共 18页由(1)知, ,
设展开式中系数最大的项为第 项,则 ,
即 ,即 ,
解得 ,所以 或 ,
所以展开式中系数最大的项为 和 .
【小问 3 详解】
由 为有理项知, 为整数,得 , ,
所以展开式中所有有理项为 和 .
17. 某市为吸引大学生人才来本市就业,大力实行人才引进计划,提供现金补贴,为了解政策的效果,收集
了 2011-2020 年人才引进就业人数数据(单位:万),统计如下(年份代码 1-10 分别代表 2011-2020 年)其
中 , , ,
.
年份代码 1 2 3 4 5 6 7 8 9 10
引进人数 3.4 5.7 7.3 8.5 9.6 10.2 10.8 11.3 11.6 11.8
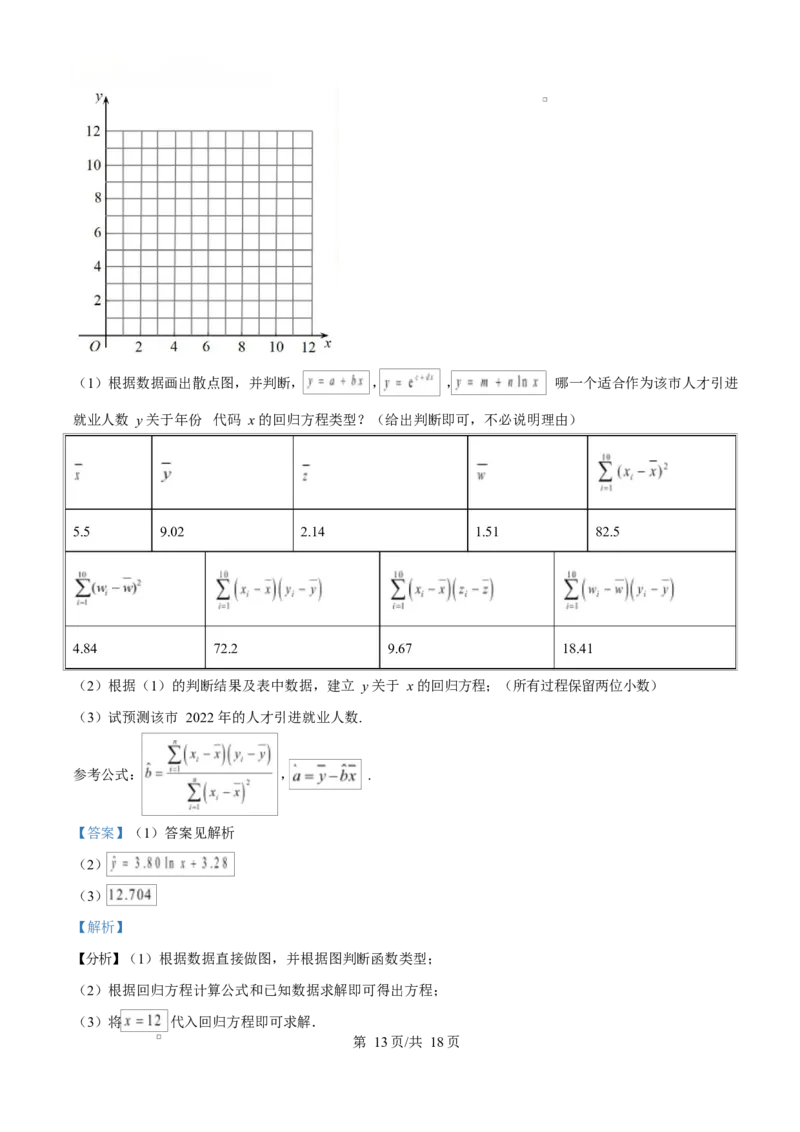
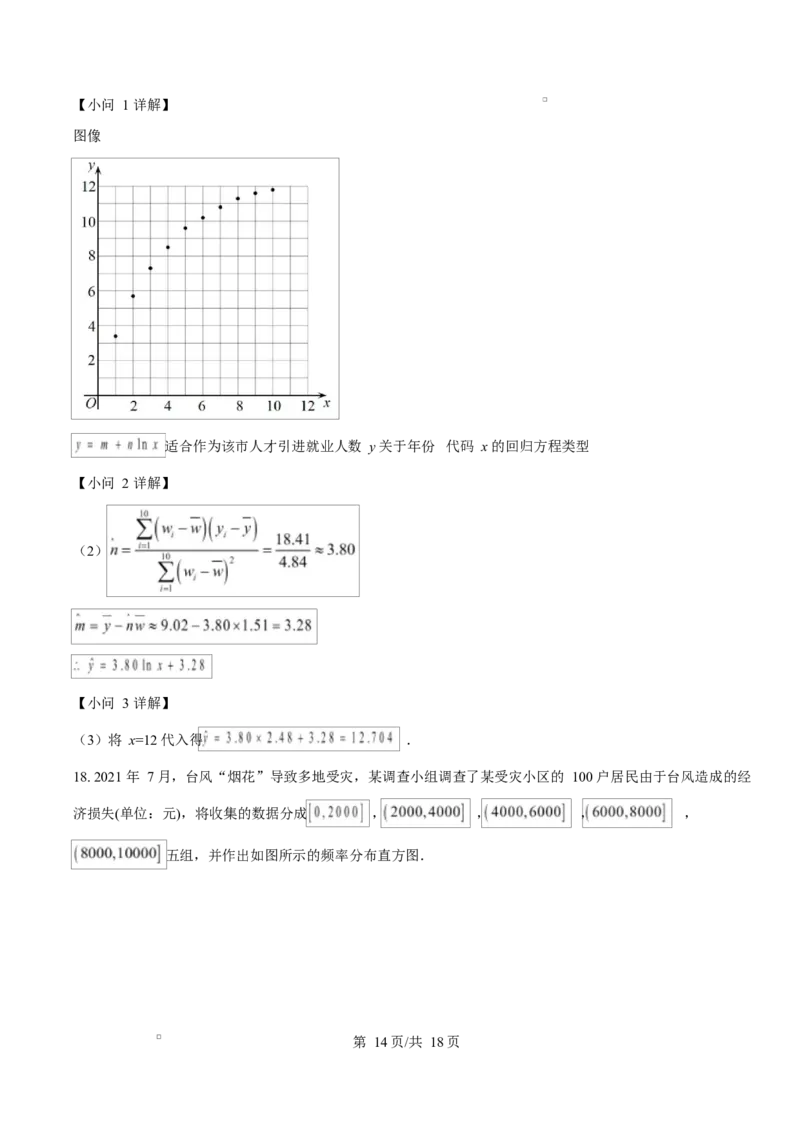
第 12页/共 18页(1)根据数据画出散点图,并判断, , , 哪一个适合作为该市人才引进
就业人数 y 关于年份 代码 x 的回归方程类型?(给出判断即可,不必说明理由)
5.5 9.02 2.14 1.51 82.5
4.84 72.2 9.67 18.41
(2)根据(1)的判断结果及表中数据,建立 y 关于 x 的回归方程;(所有过程保留两位小数)
(3)试预测该市 2022 年的人才引进就业人数.
参考公式: , .
【答案】(1)答案见解析
(2)
(3)
【解析】
【分析】(1)根据数据直接做图,并根据图判断函数类型;
(2)根据回归方程计算公式和已知数据求解即可得出方程;
(3)将 代入回归方程即可求解.
第 13页/共 18页【小问 1 详解】
图像
适合作为该市人才引进就业人数 y 关于年份 代码 x 的回归方程类型
【小问 2 详解】
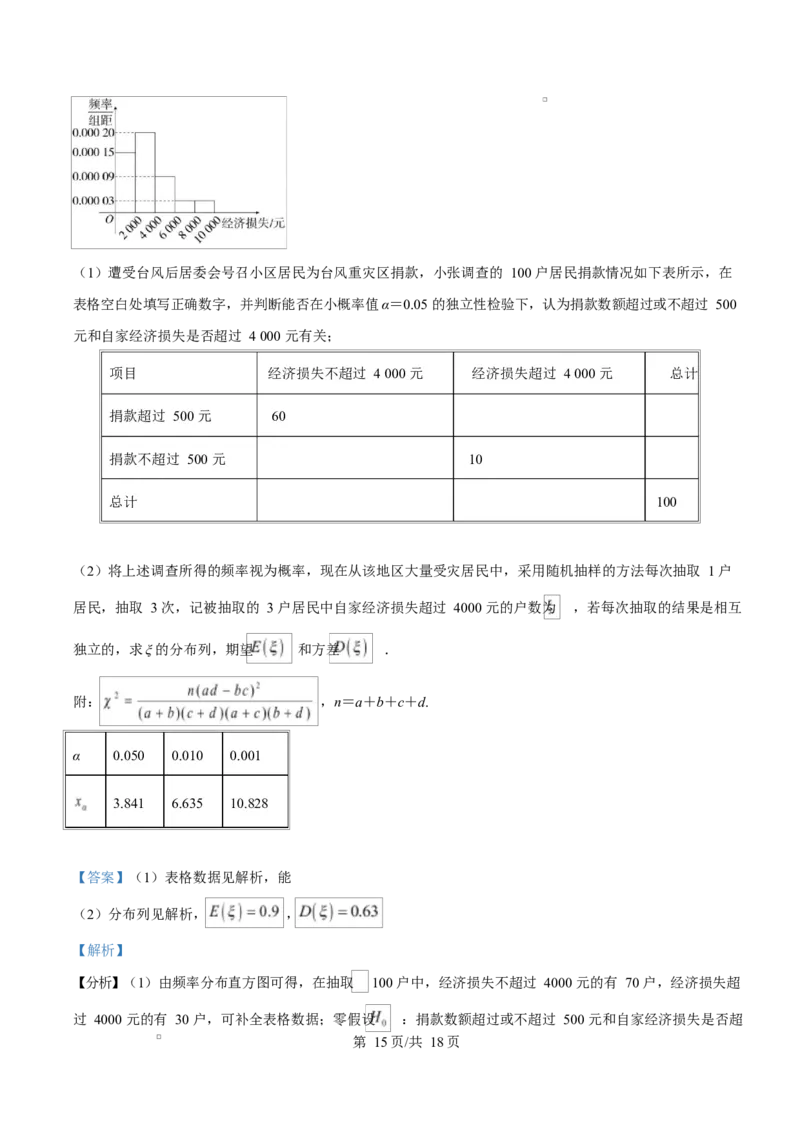
(2)
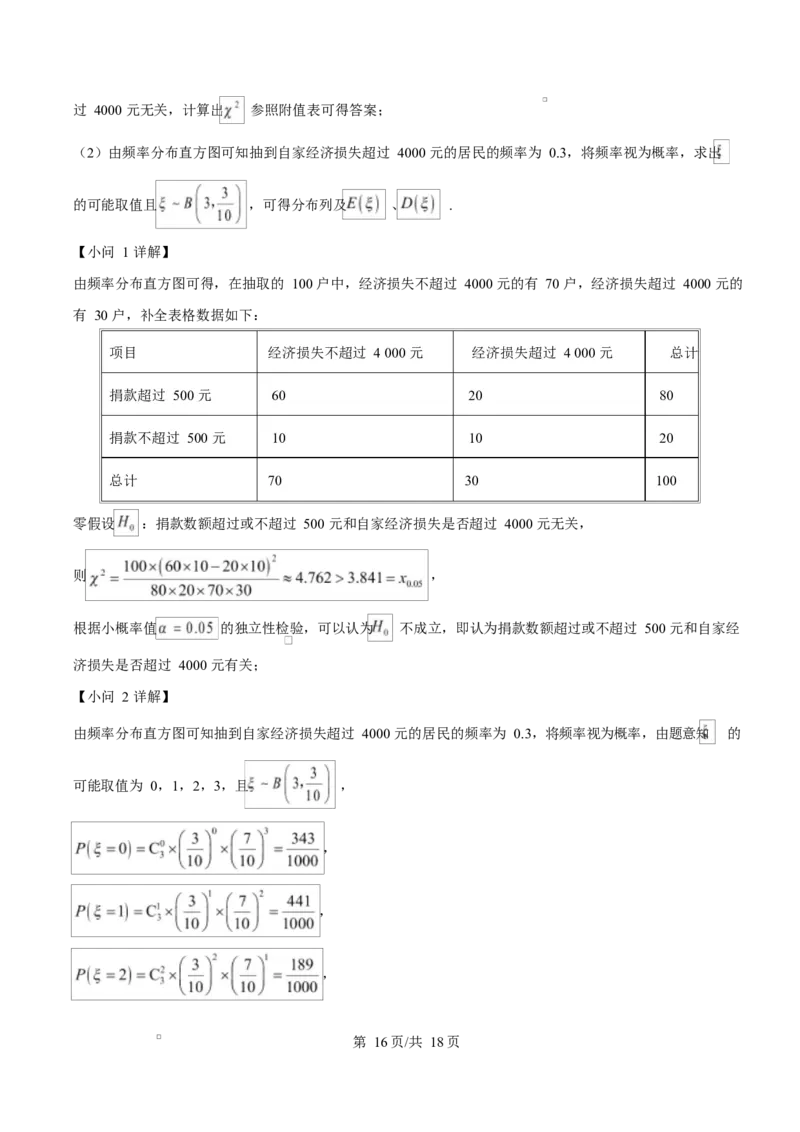
【小问 3 详解】
(3)将 x=12 代入得 .
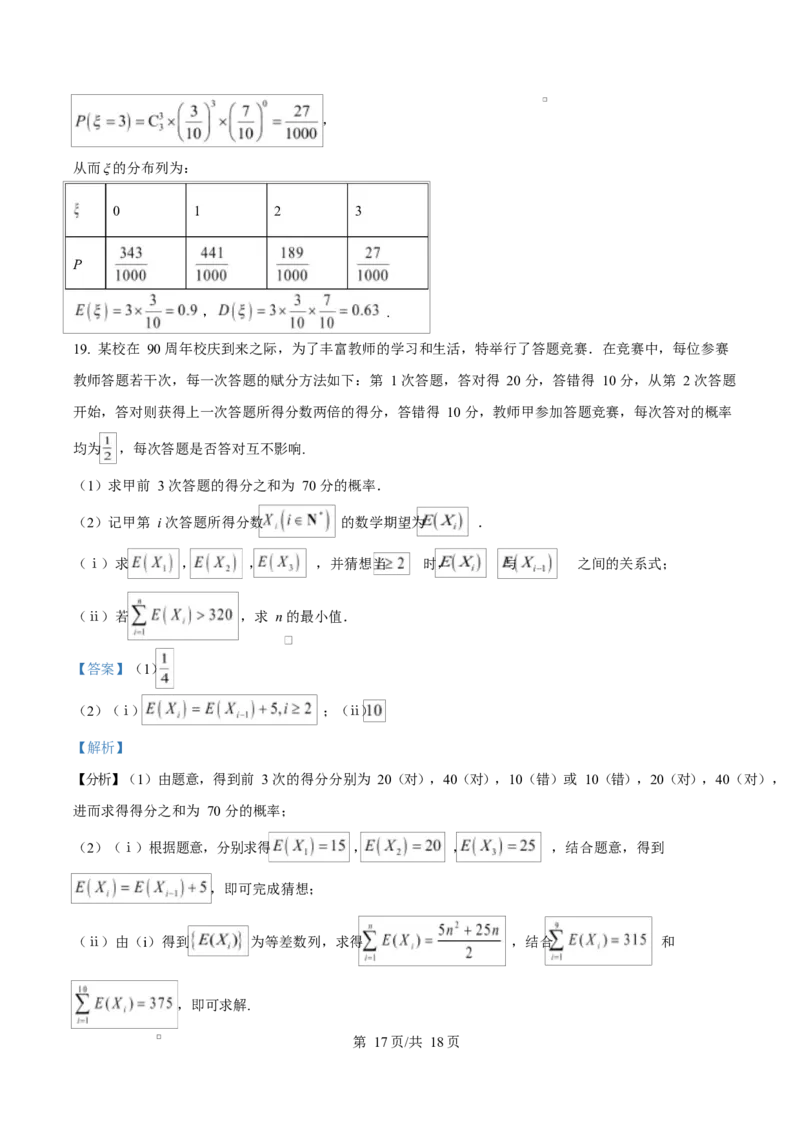
18. 2021 年 7 月,台风“烟花”导致多地受灾,某调查小组调查了某受灾小区的 100 户居民由于台风造成的经
济损失(单位:元),将收集的数据分成 , , , ,
五组,并作出如图所示的频率分布直方图.
第 14页/共 18页(1)遭受台风后居委会号召小区居民为台风重灾区捐款,小张调查的 100 户居民捐款情况如下表所示,在
表格空白处填写正确数字,并判断能否在小概率值α=0.05 的独立性检验下,认为捐款数额超过或不超过 500
元和自家经济损失是否超过 4 000 元有关;
项目 经济损失不超过 4 000 元 经济损失超过 4 000 元 总计
捐款超过 500 元 60
捐款不超过 500 元 10
总计 100
(2)将上述调查所得的频率视为概率,现在从该地区大量受灾居民中,采用随机抽样的方法每次抽取 1 户
居民,抽取 3 次,记被抽取的 3 户居民中自家经济损失超过 4000 元的户数为 ,若每次抽取的结果是相互
独立的,求ξ的分布列,期望 和方差 .
附: ,n=a+b+c+d.
α 0.050 0.010 0.001
3.841 6.635 10.828
【答案】(1)表格数据见解析,能
(2)分布列见解析, ,
【解析】
【分析】(1)由频率分布直方图可得,在抽取 100 户中,经济损失不超过 4000 元的有 70 户,经济损失超
过 4000 元的有 30 户,可补全表格数据;零假设 :捐款数额超过或不超过 500 元和自家经济损失是否超
第 15页/共 18页过 4000 元无关,计算出 参照附值表可得答案;
(2)由频率分布直方图可知抽到自家经济损失超过 4000 元的居民的频率为 0.3,将频率视为概率,求出
的可能取值且 ,可得分布列及 、 .
【小问 1 详解】
由频率分布直方图可得,在抽取的 100 户中,经济损失不超过 4000 元的有 70 户,经济损失超过 4000 元的
有 30 户,补全表格数据如下:
项目 经济损失不超过 4 000 元 经济损失超过 4 000 元 总计
捐款超过 500 元 60 20 80
捐款不超过 500 元 10 10 20
总计 70 30 100
零假设 :捐款数额超过或不超过 500 元和自家经济损失是否超过 4000 元无关,
则 ,
根据小概率值 的独立性检验,可以认为 不成立,即认为捐款数额超过或不超过 500 元和自家经
济损失是否超过 4000 元有关;
【小问 2 详解】
由频率分布直方图可知抽到自家经济损失超过 4000 元的居民的频率为 0.3,将频率视为概率,由题意知 的
可能取值为 0,1,2,3,且 ,
,
,
,
第 16页/共 18页,
从而ξ的分布列为:
0 1 2 3
P
, .
19. 某校在 90 周年校庆到来之际,为了丰富教师的学习和生活,特举行了答题竞赛.在竞赛中,每位参赛
教师答题若干次,每一次答题的赋分方法如下:第 1 次答题,答对得 20 分,答错得 10 分,从第 2 次答题
开始,答对则获得上一次答题所得分数两倍的得分,答错得 10 分,教师甲参加答题竞赛,每次答对的概率
均为 ,每次答题是否答对互不影响.
(1)求甲前 3 次答题的得分之和为 70 分的概率.
(2)记甲第 i 次答题所得分数 的数学期望为 .
(ⅰ)求 , , ,并猜想当 时, 与 之间的关系式;
(ⅱ)若 ,求 n 的最小值.
【答案】(1)
(2)(ⅰ) ;(ⅱ)
【解析】
【分析】(1)由题意,得到前 3 次的得分分别为 20(对),40(对),10(错)或 10(错),20(对),40(对),
进而求得得分之和为 70 分的概率;
(2)(ⅰ)根据题意,分别求得 , , ,结合题意,得到
,即可完成猜想;
(ⅱ)由(i)得到 为等差数列,求得 ,结合 和
,即可求解.
第 17页/共 18页【小问 1 详解】
解:由题意,前 3 次的得分分别为 20(对),40(对),10(错)或 10(错),20(对),40(对),所以甲
前 3 次答题的得分之和为 70 分的概率为 .
【小问 2 详解】
解:(ⅰ)甲第 1 次答题得分 20 分,10 分的概率分别为 ,则 ,
甲第 2 次答题得分 40 分,20 分,10 分的概率分别为 ,
则 ,
甲第 3 次答题得分 80 分,40 分,20,10 嗯分的概率分别为 ,
则 ,
当 时,因为甲第 次答题所得分数 的数学期望为 ,
所以第 次答对题所得分数为 ,答错题所的分数为 分,其概率为 ,
所以 ,
可猜想: .
(ⅱ)由(i)知数列 是以 15 为首项,5 为公差的等差数列,
根据等差数列的求和公式,可得 ,
当 时, ,当 时, ,
所以实数 的最小值为 .
【点睛】方法点睛:对于离散型随机变量的期望与方差的综合问题的求解策略:
1、理解随机变量 意义,写出 可能取得得全部数值;
2、根据题意,求得随机变量 的每一个值对应的概率;
3、列出随机变量 的分布列,利用期望和方差的公式求得数学期望和方差;
4、注意期望与方差的性质 的应用;
第 18页/共 18页