重庆市第八中学2024届高考适应性月考卷（六）数学-答案_2024年3月_013月合集_2024届重庆市第八中学高考适应性月考卷（六）_重庆市第八中学2024届高考适应性月考卷（六）数学

数学参考答案
一、单项选择题（本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只
有一项是符合题目要求的）
题号 1 2 3 4 5 6 7 8
答案 D B B A C D C B
二、多项选择题（本大题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项
是符合题目要求的．全部选对的得6分，部分选对的得部分分，有选错的得0分）
题号 9 10 11
答案 AC BCD ACD
三、填空题（本大题共3小题，每小题5分，共15分）
题号 12 13 14
10
答案 29.5 35π
2
四、解答题（共77分．解答应写出文字说明，证明过程或演算步骤）
15．（本小题满分13分）
解：（1）因为Aπ(BC)，
所以cosAcos(BC)sinBsinCcosBcosC，
2 3  π 2 3  3 1 
又cosA sinCsinB  sinC

sinB cosB

3  6 3  2 2 
3
sinBsinC sinCcosB.
3
3 2 3 1 3 
所以cosBcosC  sinCcosB，所以 cosB sinC cosC0，
 
3 3 2 2
 
1 3
所以cosB0或 sinC cosC 0， ………………………………………………（3分）
2 2
π
若cosB0，则B ，与△ABC为锐角三角形矛盾，舍去，
2
1 3
从而 sinC cosC 0，则tanC  3，
2 2
数学参考答案·第1页（共7页）π π
又0C ，所以C ．………………………………………………………………（6分）
2 3
（2）由余弦定理，得c2 a2 b2 2abcosC，即12a2 b2 ab ①，
………………………………………………………………………………………（8分）
     
设AB的中点为D，则2CDCACB，两边同时平方可得：4CD 2 (CACB)2，

即：4|CD|2a2 b2 2abcosC ，即：28a2 b2 ab ②，
……………………………………………………………………………………（10分）
由①可得：ab8，
1 1 3
于是：△ABC的面积S  absinC  8 2 3．
2 2 2
……………………………………………………………………………………（13分）
16．（本小题满分15分）
（1）证明：取BD中点O，连接AO，CO，菱形ABCD中，AB AD，CBCD，
所以AOBD，COBD，又因为AOCOO，
所以BD平面AOC ，…………………………………………………………………（4分）
又AC平面AOC，所以ACBD．………………………………………………（6分）
π 2π
（2）解：△ABD中，因为ABC  ，所以BAD ，
3 3
由余弦定理得BD2 BC2 CD2 2BCCDcosBCD12，解得BD2 3；
在△AOC中，AOCO1，
AO2 CO2 AC2 1 2π
所以cosAOC   ，AOC  ．…………………………（8分）
2AOCO 2 3

在平面AOC中，作OEOC，交AC于点E，则以O为坐标原点，分别以OC方向为x
轴正方向，建立如图所示空间直角坐标系，
 1 3
则A ，0， ． ………………………………（9分）
 
2 2
 
又C(1，0，0)，B(0， 3，0)，D(0， 3，0)，
假设在线段BD上存在符合要求的点G(0，m，0)( 3≤m≤ 3)．

设平面ACG的法向量n (x，y，z)，
1
数学参考答案·第2页（共7页） 3 3 
由AC  ，0， ，CG(1，m，0)，
 
2 2
 
  3 3
ACn  x z0 
则 1 2 2 ，取n (m，1， 3m)． …………………………………（11分）
   1
CGn xmy0
1

平面BCD的法向量n (0，0，1)；
2
 
  |n n | | 3m| 21 3
所以|cosn，n | 1 2   ，m ．
1 2 |n ||n | m2 13m2 7 3
1 2
……………………………………………………………………………………（13分）
3 4 3 3 2 3
当m 时，BG ；当m 时，BG ．
3 3 3 3
4 3 2 3 21
所以当BG 或 时，平面ACG与平面BCD所成角的余弦值为 ．
3 3 7
…………………………………………………………………………………（15分）
17．（本小题满分15分）
xcosxsinx π 4
解：（1） f(x) sinx， f  1 ．……………………………（2分）
x2 2 π2
π 2
因为 f   ，
2 π
2  4  π  4  4 π
所以切线方程为y 1 x ，即y1 x  ．
π  π2  2  π2  π 2
……………………………………………………………………………………（6分）
（2）由题意，sinxxcosxax3 0．
令g(x)sinxxcosxax3，则g(x)xsinx3ax2 x(sinx3ax)．
……………………………………………………………………………………（7分）
令h(x)sinx3ax，h(x)cosx3a．
1
①当3a1，即a 时，h(x)0，h(x)在(0，)单调递增，h(x)h(0)0，
3
所以g(x)0，g(x)在(0，)单调递增，g(x)g(0)0，不合题意．
…………………………………………………………………………………（10分）
数学参考答案·第3页（共7页）1
②当3a1，即a 时，h(x)0，h(x)在(0，)单调递减，h(x)h(0)0，
3
所以g(x)0，g(x)在(0，)单调递减，所以g(x)g(0)0，符合题意．
…………………………………………………………………………………（12分）
1 1
③当13a1，即 a 时，由h(0)13a0，h(π)13a0，
3 3
所以x (0，π)，使得h(x )0且x(0，x )时，h(x)0，
0 0 0
所以g(x)0，g(x)在(0，x )单调递增，g(x )g(0)0，不符合题意．
0 0
1
综上，a ．……………………………………………………………………………（15分）
3
18．（本小题满分17分）
解：（1）设事件A “第k个月销路好”，B “第k个月销路差”．
k k
由题意，知P(A )P(A |A )P(A )P(A |B )P(B )，
k1 k1 k k k1 k k
P(B )P(B |A )P(A )P(B |B )P(B )．
k1 k1 k k k1 k k
x 0.5x 0.4y，
即： k1 k k ……………………………………………………………（2分）
y 0.5x 0.6y .
k1 k k
当x  y 0.5时，x 0.5x 0.4y 0.45；
1 1 2 1 1
y 0.5x 0.6y 0.55，x 0.5x 0.4y 0.445．…………………………………（4分）
2 1 1 3 2 2
5x 4y 5(0.5x 0.4y )4(0.5x 0.6y )
k1 k1 k k k k
0.5x 0.4y 0.1(5x 4y )．
k k k k
因为5x 4y 0.5，所以{5x 4y }是首项为0.5，公比为0.1的等比数列．
1 1 k k
……………………………………………………………………………………（6分）
（2）如果第一个月销路好，则x 1，y 0，5x 4y 5．
1 1 1 1
 1  k1
由（1）知，5x 4y 5  ．
k k 10
5  1  k1 1 2 1  1  k1
所以y  x   ．所以x  x  y x    ．
k 4 k 10  k1 2 k 5 k k 2 10
…………………………………………………………………………………（10分）
数学参考答案·第4页（共7页）1  1  k2 1  1  k2  1  k3
从而x x    x      
k k1 2 10 k2 2 10 10 
1  1  k2  1  k3  1  k4
x      +  
k3 2 10 10 10 

1  1  k2  1  k3  1  k4  4 5  1  k1
x      +  1    ．
1 2 10 10 10  9 9 10
4 5  1  k1
即x     ．…………………………………………………………………（13分）
k 9 9 10
如果第一个月销路差，则x 0，y 1，5x 4y 4．
1 1 1 1
4 4  1  k1
同理可得，x     ．
k 9 9 10
可以看到，无论第一个月销路好还是销路差，经过较长时间的销售之后，销路好的概率
4
会趋近于常数 ．………………………………………………………………………（17分）
9
19．（本小题满分17分）
解：（1）设Q(x，y)，则P(x，2y)，因为P在圆O上，
x2
所以x2 4y2 4，即  y2 1，
4
x2
所以C的方程为  y2 1．
4
C是长轴长为4，焦点为( 3，0)，( 3，0)的椭圆．………………………………（4分）
（2）先证明BM∥OT，且B，N，M 共线．
1 1
x2
由（1）知C：  y2 1，故A(2，0)，A (2，0)，B(0，1)，B (0，1)，
4 1 2 1 2
直线A B 的方程为x2y20．
2 2
当OT 斜率不存在的时候，直线l 与C仅有一个公共点，不合题意，所以OT 斜率存在，
1
1
设直线OT：ykx，因为当OT∥AB 时，A与B 重合，不合题意，所以k  ．
1 2 2 2
当OT 斜率为零时，直线BT 与x轴重合，不合题意，
数学参考答案·第5页（共7页）又因为点T在线段A B 上，所以k 0．
2 2
1
综上，k 0，且k  ．…………………………………………………………………（6分）
2
ykx，  2 2k 
由 得T ， ，
x2y20. 12k 12k
因为l∥OT ，所以l：yk(x2)，则B(0，2k)，
1 1
1 
由k k ，得N ，0， ……………………………………………………………（9分）
BT BN k 
yk(x2)，

设A(x ，y )，由x2 得(14k2)x2 16k2x16k2 40，
1 1   y2 20.
 4
16k2 4 28k2 4k
故2x  ，所以x  ， y kx 2 ，
1 14k2 1 14k2 1 1 14k2
28k2 4k 
即A ， ．………………………………………………………………（12分）
14k2 14k2

易得，BN：ykx1，则BN//l ，设BN交C于M (x ，y )，
1 1 1 1 1 2 2
ykx1，
 8k
由x2 得(14k2)x2 8kx0，故x  ．
  y2 1. 2 14k2
 4
解法一：
8k 1 4k2 1 |M N| x x 1 |ON| |TN|
x x    ， 1  2 N    ，
2 N 14k2 k k(14k2) |AB| x 2k |OA | |TB|
1 1
2(4k2 1)2
又(x x )(x x ) 0．
2 N B 1 k(14k2)2
 
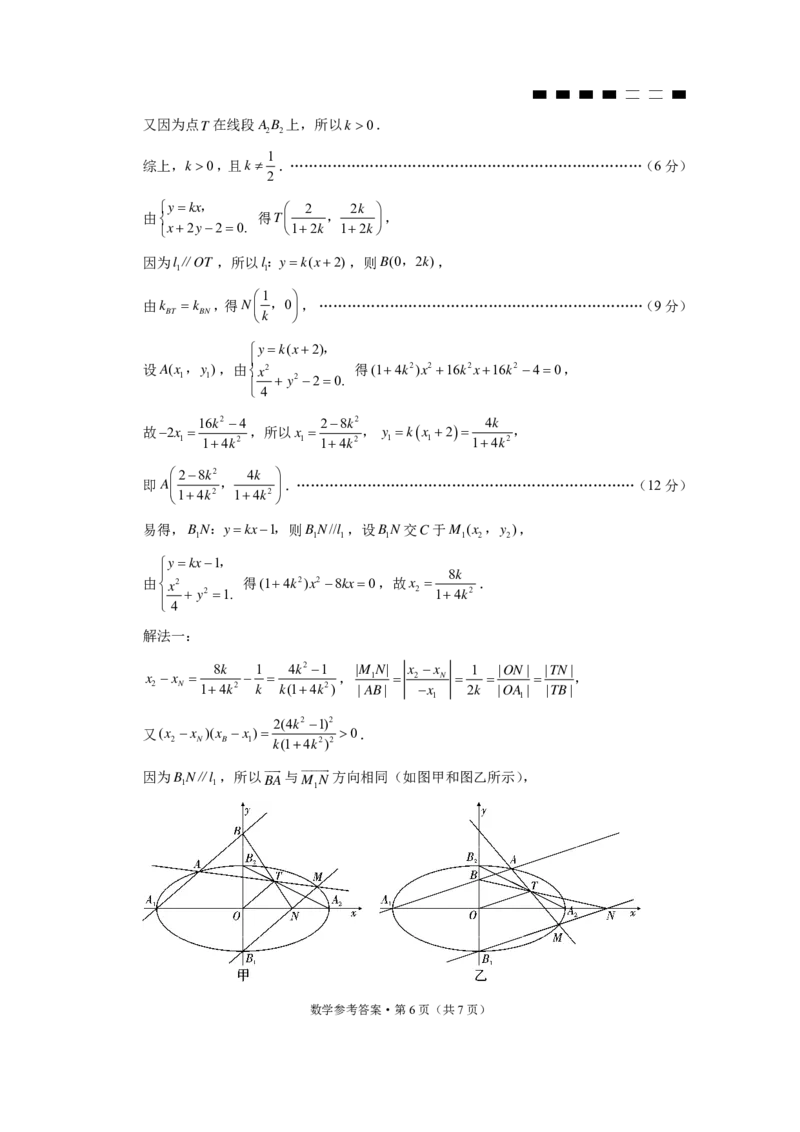
因为BN∥l ，所以BA与M N 方向相同（如图甲和图乙所示），
1 1 1
数学参考答案·第6页（共7页）所以A，T，M 三点共线，从而M，M 重合，故BM∥OT，且B，N，M 共线．
1 1 1 1
解法二：
4k2 1
y kx 1 ，
2 2 14k2
4k2 1 2k

14k2 12k (4k2 1)(12k)2k(14k2) 4k2 4k1
所以k    ，
M1T 8k 2 8k(12k)2(14k2) 8k2 8k2

14k2 12k
4k 2k 2k k
 
14k2 12k 14k2 12k 2k(12k)k(14k2) 4k2 4k1
k     ，
AT 28k2 2 14k2 1 (14k2)(12k)(14k2) 8k2 8k2
 
14k2 12k 14k2 12k
故k k ，所以A，T，M 三点共线，BM∥OT，且B，N，M 共线．
M1T AT 1 1 1
1 4k 28k2
因为k 0，且k  ，所以2k  ，（或利用 0）
2 14k2 14k2
所以A，B不重合，A，N，T 不共线．
|MT | |TN|
若选①，则由BM∥OT，且B，N，M 共线，得  ，
1 1 |AT | |TB|
即|AT ||NT ||BT ||MT |． …………………………………………………………（17分）
若选②，则由BM∥OT，且B，N，M 共线，得△ABN 与△ABM 面积相等，
1 1
所以，△ATM 与△BTM 面积相等．…………………………………………………（17分）
数学参考答案·第7页（共7页）