文档内容
2024-2025 学年河南省部分名校高二下学期 3 月大联考数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
m
1.已知函数f(x)=− ,f ′(x)为f(x)的导函数,且f ′(1)=2,则实数m=( )
x
1
A. 0 B. C. 1 D. 2
2
x2 y2
2.双曲线C: − =1的渐近线方程为( )
12 3
1 1
A. y=± x B. y=± x C. y=±2x D. y=±4x
4 2
3.已知{a }是等比数列,若a a =2a ,a =16,则{a }的公比q=( )
n 3 8 5 9 n
1 1
A. 4 B. 2 C. D.
2 4
4.已知矩形ABCD的边AB所在直线的方程为2x−y+4=0,顶点D(0,−1),则顶点A的坐标为( )
A. (−2,0) B. (−1,0) C. (1,0) D. (2,0)
5.若存在 ,使得直线 与圆 相切,则实数 的取值范围为( )
a∈R ax+2y−b=0 C:x2+(y+1) 2=1 b
A. (−∞,−4] B. [0,+∞)
C. [−4,0] D. (−∞,−4]∪[0,+∞)
6.在正四棱柱ABCD−A B C D 中,A A =2AB=4,E,F分别为AB ,BC 的中点,点G为上底面
1 1 1 1 1 1 1
A B C D 的中心,则直线EG与DF夹角的余弦值为( )
1 1 1 1
√5 √5 √3 √3
A. B. C. D.
5 3 5 3
7.已知某圆柱的表面积为4π,则该圆柱的体积的最大值为( )
2√6 5√6 4√6 √6
A. π B. π C. π D. π
3 9 9 3
8.已知 ,函数 , ,当 时,函数 的图象始终在函数 的图象下
a>1 f(x)=1+log x g(x)=a2x2 x>0 f(x) g(x)
a
方(所有点均不重合),则实数a的取值范围为( )
1 1 1 1
A. B. C. D.
(1,e2e) (1,ee) (e2e,+∞) (ee,+∞)
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.记S 为等差数列{a }的前n项和,已知a =4,S =0,则下列结论正确的有( )
n n 7 9
第 页,共 页
1 1A. a =−10 B. a =2n−10
1 n
C. S =220 D. 数列{S }中有且仅有一个最小项
20 n
10.已知函数 ,则下列结论正确的有( )
f(x)=m(x−1) n (x−m)(m≠0,n∈N∗)
A. 当n=1,m<0时,f(x)只有最大值,无最小值
B. 当n=1,m>0时,f(x)有两个极值点
C. 当n=2,m>1时,x=1是f(x)的极大值点
D. 当n=2,01,f(x)>f(√x)
11.已知点P(x ,y )在曲线C:x4−2x2+ y2=0上,点F(1,0),则下列结论正确的有( )
0 0
A. 曲线C关于原点对称
B.
−√2≤x ≤√2
0
C. |PF|的最小值为1
1
D. 曲线C与x轴的非负半轴、直线x=1所围成区域的面积大于
2
三、填空题:本题共3小题,每小题5分,共15分。
12.已知 m∈R ,向量⃗ a=(1,m,−2) ,⃗ b=(m,2,3) ,若⃗ a⋅ ⃗ b=6 ,则 |⃗a|= .
13.已知圆 与圆 的相交弦所在直线为 ,若 与抛物线 交于 ,
C :x2+ y2=4 C :x2+ y2+2x−y−6=0 l l y2=4x A
1 2
B两点,则|AB|= .
14.数列 的通项公式为 ,则 的前 项和 为 用含 的式子表示 .
{a } a =(2n−1)⋅4n {a } n S ( n )
n n n n
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题12分)
ex
已知函数f(x)= (a>0),曲线y=f(x)在(0,f(0))处切线的斜率为−2.
x−a
(1)求实数a的值;
(2)研究f(x)的单调性;
(3)求f(x)的极值.
16.(本小题12分)
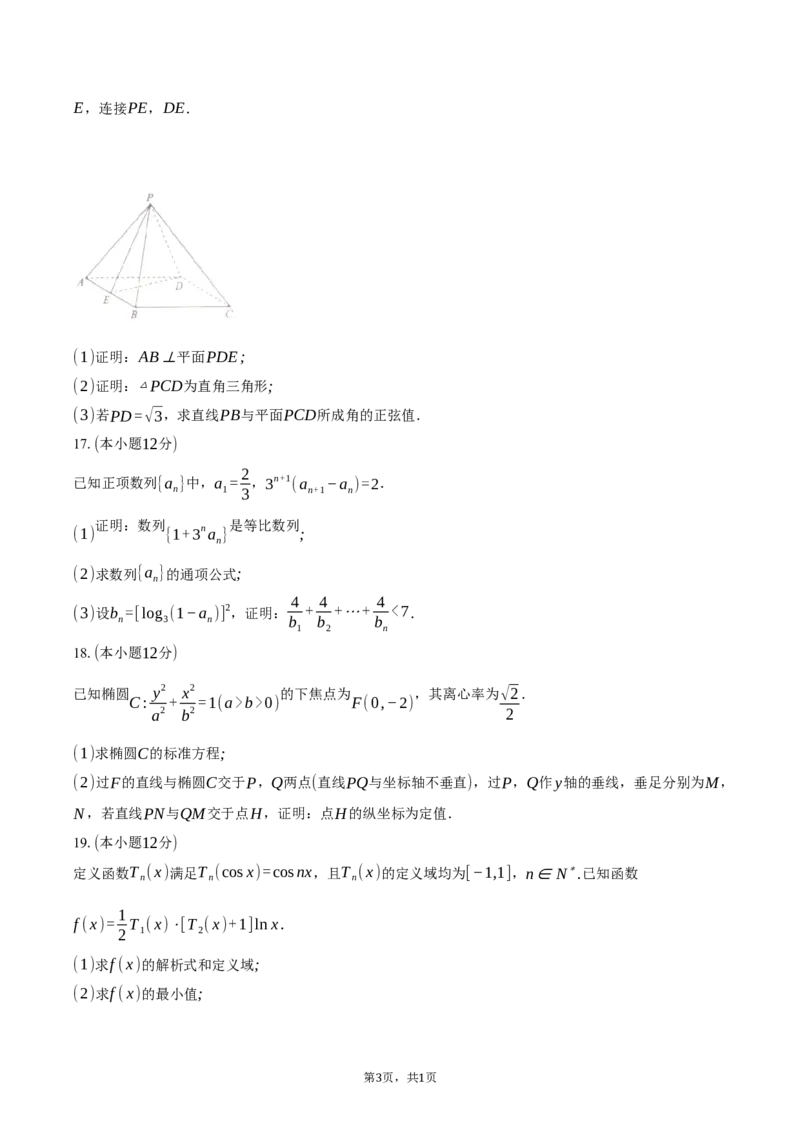
如图,四棱锥P−ABCD的底面为菱形,∠BAD=60∘,且侧面PAB是边长为2的等边三角形.取AB的中点
第 页,共 页
2 1E,连接PE,DE.
(1)证明:AB⊥平面PDE;
(2)证明:△PCD为直角三角形;
(3)若PD=√3,求直线PB与平面PCD所成角的正弦值.
17.(本小题12分)
2
已知正项数列{a }中,a = ,3n+1 (a −a )=2.
n 1 3 n+1 n
证明:数列 是等比数列
(1) {1+3na } ;
n
(2)求数列{a }的通项公式;
n
4 4 4
(3)设b =[log (1−a )] 2,证明: + +⋯+ <7.
n 3 n b b b
1 2 n
18.(本小题12分)
已知椭圆 y2 x2 的下焦点为 ,其离心率为√2.
C: + =1(a>b>0) F(0,−2)
a2 b2 2
(1)求椭圆C的标准方程;
(2)过F的直线与椭圆C交于P,Q两点(直线PQ与坐标轴不垂直),过P,Q作y轴的垂线,垂足分别为M,
N,若直线PN与QM交于点H,证明:点H的纵坐标为定值.
19.(本小题12分)
定义函数T (x)满足T (cosx)=cosnx,且T (x)的定义域均为[−1,1],n∈N∗.已知函数
n n n
1
f(x)= T (x)⋅[T (x)+1]lnx.
2 1 2
(1)求f(x)的解析式和定义域;
(2)求f(x)的最小值;
第 页,共 页
3 1若 , 是 的两个实根,证明: 2 1 .
(3) x x (00),所以f ′(x)=
x−a−1
ex ,由题意可知,f ′(0)=
−a−1
=−2,
x−a (x−a) 2 a2
1
解得a=1或a=− (舍去),故实数a的值为1;
2
(2)(2)f(x)的定义域为{x|x≠1},
x−2
由(1)可知,f ′(x)= ex ,
(x−1) 2
令f ′(x)=0,解得x=2,当x∈(−∞,1)∪(1,2)时,f ′(x)<0,当x∈(2,+∞)时,f ′(x)>0,
故f(x)在(−∞,1),(1,2)上单调递减,在(2,+∞)上单调递增,
(3)由(2)知,f(x)在(1,2)上单调递减,在(2,+∞)上单调递增,
e2
故f(x)在x=2处取得极小值,极小值为f(2)= =e2,无极大值.
2−1
16.(1)证明:因为侧面PAB是等边三角形,E为AB的中点,所以PE⊥AB.
因为四边形ABCD为菱形,且∠BAD=60∘,所以DE⊥AB.
又PE∩DE=E,PE,DE⊂平面PDE,AB⊂平面PDE,所以AB⊥平面PDE.
第 页,共 页
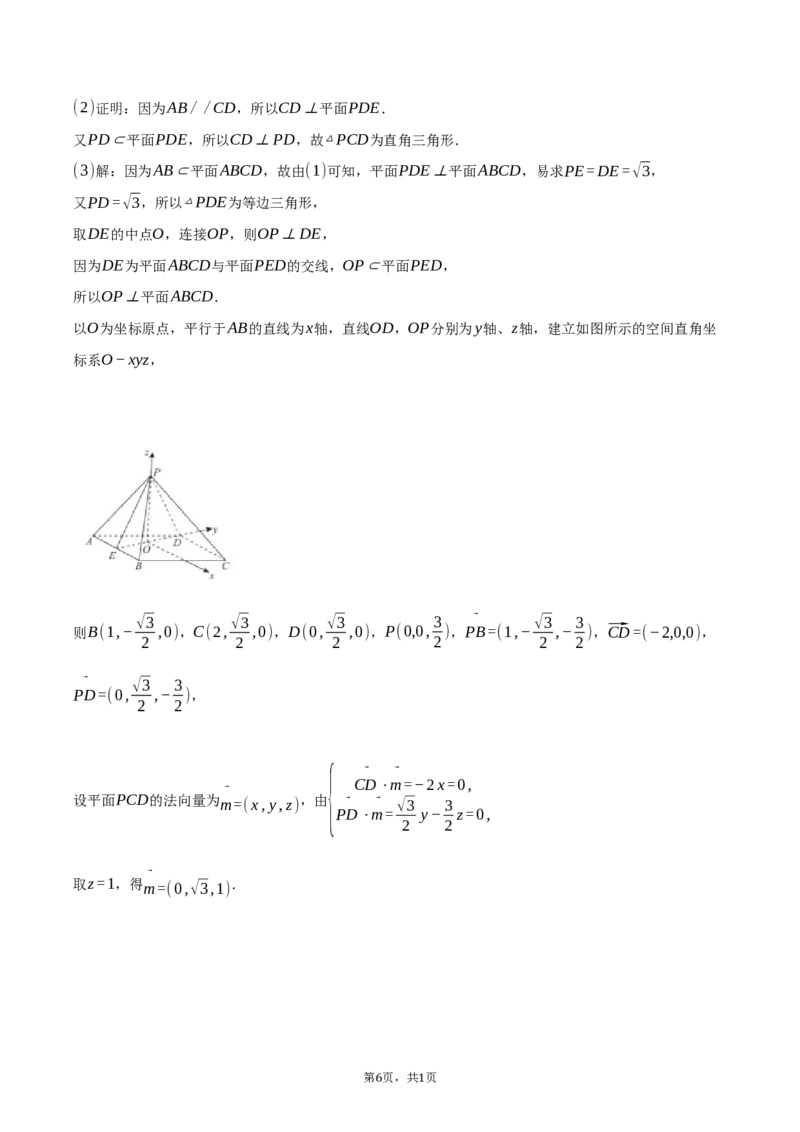
5 1(2)证明:因为AB//CD,所以CD⊥平面PDE.
又PD⊂平面PDE,所以CD⊥PD,故△PCD为直角三角形.
(3)解:因为AB⊂平面ABCD,故由(1)可知,平面PDE⊥平面ABCD,易求PE=DE=√3,
又PD=√3,所以△PDE为等边三角形,
取DE的中点O,连接OP,则OP⊥DE,
因为DE为平面ABCD与平面PED的交线,OP⊂平面PED,
所以OP⊥平面ABCD.
以O为坐标原点,平行于AB的直线为x轴,直线OD,OP分别为y轴、z轴,建立如图所示的空间直角坐
标系O−xyz,
√3 √3 √3 3 ⃗ √3 3
则B(1,− ,0),C(2, ,0),D(0, ,0),P(0,0, ),PB=(1,− ,− ),⃗CD=(−2,0,0),
2 2 2 2 2 2
⃗ √3 3
PD=(0, ,− ),
2 2
⃗ ⃗
{
CD⋅m=−2x=0,
⃗
设平面PCD的法向量为m=(x,y,z) ,由 ⃗ ⃗ √3 3
PD⋅m= y− z=0,
2 2
⃗
取z=1,得m=(0,√3,1) .
第 页,共 页
6 1⃗ ⃗
设直线PB与平面PCD所成的角为θ,则 sinθ=|cos|=
|m⋅PB|
=
3
=
3
,
⃗ ⃗ 2×2 4
|m||PB|
3
故直线PB与平面PCD所成角的正弦值为 .
4
17. 证明:由 得, ,
(1) 3n+1 (a −a )=2 3n+1a =2+3n+1a
n+1 n n+1 n
则 ,
1+3n+1a =3+3n+1a =3×(1+3na
)
n+1 n n
1+3n+1a
因为 a >0 ,所以 n+1=3 ,
n 1+3na
n
2
又1+3a =1+3× =3,故数列{1+3na }是首项为3,公比为3的等比数列.
1 3 n
解:由 可知, ,故 3n−1 1 .
(2) (1) 1+3na =3×3n−1=3n a = =1−( ) n
n n 3n 3
1
(3)证明:由(2)得,b =[log (1−a )] 2=[log ( ) n ] 2=n2,
n 3 n 3 3
4
当n=1时, =4<7,不等式成立;
b
1
4 4 4
当n=2时, + =4+ =5<7,不等式成立;
b b 22
1 2
1 1 1 1
当n≥3时, < = − ,
n2 n(n−1) n−1 n
4 4 4 1 1 1 1 1 1 1 4 4
所以 + +⋯+ <4[1+ +( − )+( − )+⋯+( − )]<5+(2− )=7− <7,
b b b 22 2 3 3 4 n−1 n n n
1 2 n
4 4 4
综上可知, + +⋯+ <7.
b b b
1 2 n
第 页,共 页
7 1{a2−b2=4,
18.解: 由题意可知, 解得 , ,
(1) 2 √2 a2=8 b2=4
= ,
a 2
y2 x2
故椭圆C的标准方程为 + =1;
8 4
(2)证明:设直线PQ的方程为y=kx−2(k≠0),P(x ,y ),Q(x ,y ),则M(0,y ),N(0,y ),
1 1 2 2 1 2
{y2 x2
由 + =1,得 ,显然, ,
8 4 (k2+2)x2−4kx−4=0 Δ>0
y=kx−2,
4k 4
则x +x = ,x x =− ,
1 2 k2+2 1 2 k2+2
易知直线 与 的斜率均存在,则直线 的方程为 y −y ,
PN QM PN y=− 2 1 x+ y ①
x 2
1
直线 的方程为 y −y ,
QM y= 2 1 x+ y ②
x 1
2
联立 消去 得, x y +x y
①)② x y= 1 2 2 1
x +x
1 2
8k
−
x (kx −2)+x (kx −2) 2kx x k2+2
= 1 2 2 1 =−2+ 1 2=−2+ =−4,
x +x x +x 4k
1 2 1 2
k2+2
故点H的纵坐标为定值−4.
19.解:(1)由题意得,T (cosx)=cosx,故T (x)=x,
1 1
又 ,所以 ,
T (cosx)=cos2x=2cos2x−1 T (x)=2x2−1
2 2
第 页,共 页
8 1故 , 的定义域为 .
f(x)=x3lnx f(x) (0,1]
,
(2)f ′(x)=3x2lnx+x2=x2 (3lnx+1)
令f ′(x)=0,解得
x=e
−
3
1,
1 1
当
x∈(0,e
−
3)
时,f ′(x)<0,f(x) 单调递减;当
x∈(e
−
3,1]
时,f ′(x)>0,f(x) 单调递增,
故 − 1 − 1 − 1 1 ;
f(x) =f(e 3)=(e 3) 3lne 3=−
min 3e
(3)证明:因为x ,x (00 ,
x 2 1
1 +
x3 x3
1 2
x
1−( 2 ) 3
x x
即证 ln 2+ 1 >0 ,
x x
1 2( 2 ) 3+1
x
1
令 x ,则只需证 1−m3 ,
m= 2 (m>1) lnm+ >0
x 2m3+1
1
设
1−m3
,
g(m)=lnm+ (m>1)
2m3+1
则 1 9m2 4m6−5m3+1
g′(m)= − =
m (2m3+1) 2 m(2m3+1) 2
(4m3−1)(m3−1)
,
= >0
m(2m3+1) 2
所以g(m)在(1,+∞)上单调递增,
则 ,所以
1−m3
成立,
g(m)>g(1)=0 lnm+ >0
2m3+1
故 2 1 .
a( + )<−1
x3 x3
1 2
第 页,共 页
10 1