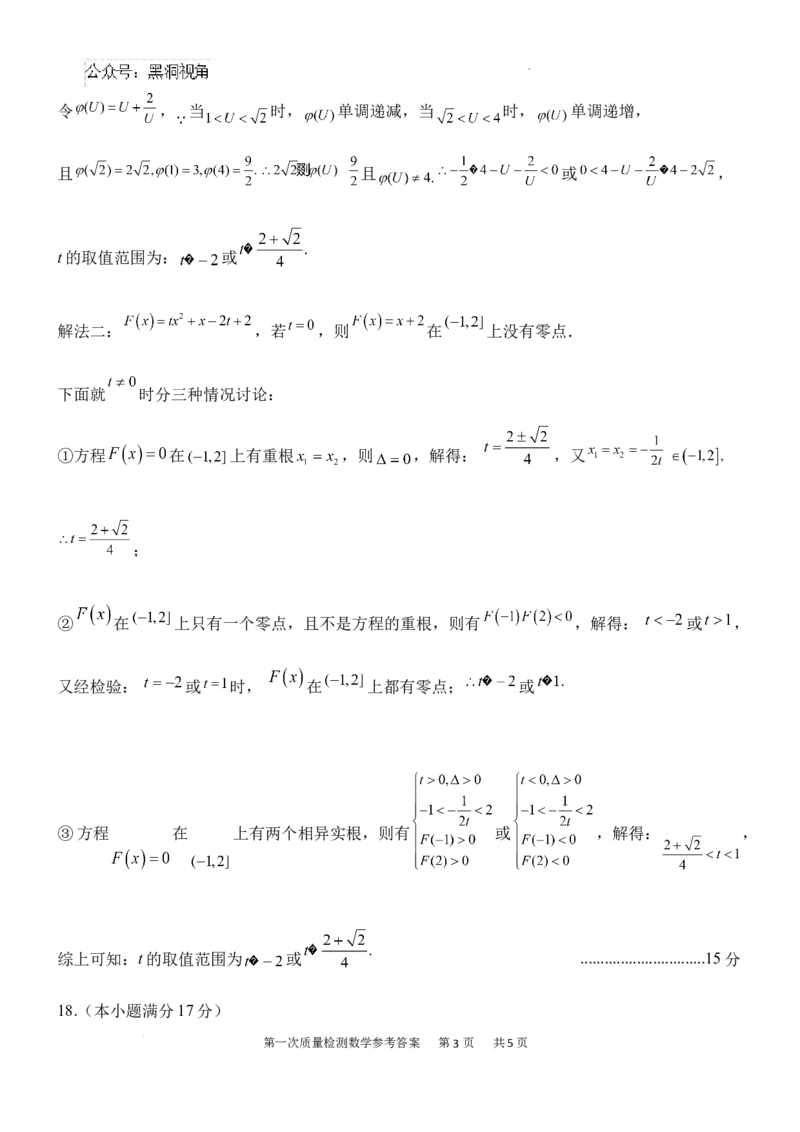文档内容
陕西省西安中学高 2025 届高三第一次质量检测
数学参考答案
一. 选择题(本题共8小题,每小题5分,共40分)
题号 1 2 3 4 5 6 7 8
答案 C B A B D C D A
二. 选择题(本题共3小题,每小题6分,共18分)
题号 9 10 11
答案 ACD BCD ABD
三、填空题:(本题共3小题,每小题5分,共15分.)
12. 6 5 13. 14. 40
三、解答题:(本题共5小题,其中第15题13分,第16,17题15分,第18,19题17分,共77分)
15.(本小题满分13分)
解: 时, ,
所以 或 时, ; 时,
则 在 上递减,在 上递增,
所以 的极小值为 ,极大值为 ...............................5分
,则 ,当 时, ,所以 在
上 递 增 , 当 时 , 或 时 , ; 时 , , 所 以
在 上递增,在 上递减,当 时, 或 时, ;
第一次质量检测数学参考答案 第 1 页 共5页
学科网(北京)股份有限公司时,
所以 在 上递增;在 上递减. ...............................8分
16.(本小题满分15分)
解:(1)解:由 得 ,
由题意得 , ,
所以 ,
,
所以 ,
即y关于x的经验回归方程为 , ...............................10分
(2)令 ,所以 ,解得 ,由于 ,所以 ,
所以从第十个月开始,该年级体重超标的人数降至10人以下. ...............................5分
17.(本小题满分15分)
解: 时, ,又 , ,
, 解集为: ;
...............................6 分
解法一: ,由 得: 且 ,
,设 且 ,则 ,
第一次质量检测数学参考答案 第 2 页 共5页
学科网(北京)股份有限公司令 , 当 时, 单调递减,当 时, 单调递增,
且 且 或 ,
t的取值范围为: 或
解法二: ,若 ,则 在 上没有零点.
下面就 时分三种情况讨论:
①方程 在 上有重根 ,则 ,解得: ,又
;
② 在 上只有一个零点,且不是方程的重根,则有 ,解得: 或 ,
又经检验: 或 时, 在 上都有零点; 或
③方程 在 上有两个相异实根,则有 或 ,解得: ,
综上可知:t的取值范围为 或 ...............................15分
18.(本小题满分17分)
第一次质量检测数学参考答案 第 3 页 共5页
学科网(北京)股份有限公司由题意,估计从该品牌芯片的生产线中随机抽取100件的平均数为:
即
,所以X∽ ,因为质量指标值X近似服从正态分布 ,
所以 ,
所以从生产线中任取一件芯片,该芯片为A等品的概率约为
...............................5 分
,所以所取样本的个数为 20件,质量指标值在 的芯片件数为
10件,故 可能取的值为0,1,2,3,相应的概率为:
, ,
, ,
随机变量 的分布列为:
0 1 2 3
P
所以 的数学期望 ...............................11分
设每箱产品中A等品有Y件,则每箱产品中B等品有 件,设每箱产品的利润为Z元,
由题意知: ,
第一次质量检测数学参考答案 第 4 页 共5页
学科网(北京)股份有限公司由 知:每箱零件中A等品的概率为 ,所以Y∽ ,所以 ,
所以
,令
得, ,又 , , 递增 , , 递
减,所以当 时, 取得最大值.所以当 时,每箱产品利润最大.
...............................17分
19.(本小题满分17分)
解:当 时, ,且知 ,在 上, , 在 上单
调递增;在 上, , 在 上单调递减;所以函数 的单调增区间为 ,
单调减区间为
..............................4分
证明:因为 ,所以 ,且知 ,
要证函数 单调递增,即证 在 上恒成立,
设 , ,则 ,
注意 , 在 上均为增函数,故 在 上单调递增,且 ,
于是 在 上单调递减,在 上单调递增, ,即 ,因此函数 在
第一次质量检测数学参考答案 第 5 页 共5页
学科网(北京)股份有限公司上单调递增;
...............................10分
由 ,有 ,令 ,有 ,
①当 时, 在 上恒成立,因此 在 上单调递减,
注意到 ,故函数 的增区间为 ,减区间为 ,此时 是函数 的极大值点;
②当 时, 与 在 上均为单调增函数,故 在 上单调递增,
注意到 ,若 ,即 时,此时存在 ,使 ,
因此 在 上单调递减,在 上单调递增,又知 ,
则 在 上单调递增,在 上单调递减,此时 为函数 的极大值点,
若 ,即 时,此时存在 ,使 ,
因此 在 上单调递减.在 上单调递增,又知 ,
则 在 上单调递减,在 上单调递增,此时 为函数 的极小值点.
当 时,由 可知 单调递增,因此 非极大值点,
综上所述,实数 a的取值范围为 ..........................17分
第一次质量检测数学参考答案 第 6 页 共5页
学科网(北京)股份有限公司