数学参考答案_2024-2025高三（6-6月题库）_2024年11月试卷_1111福建省福宁古五校教学联合体2024-2025学年第一学期期中质量监测

福宁古五校教学联合体 2024-2025 学年第一学期期中质量监测 高三数学参考答案 一、单选题 1 2 3 4 5 6 7 8 A C D C C D B D 8．解： f (x)1，e2x+lnx −(2x+lnx)+x−|a|x1，即 e2x+lnx −(2x+lnx)−1 |a|−1 ，易知ex  x+1，e2x+lnx −(2x+lnx)−10，又 x e2x+lnx −(2x+lnx)−1 x0， 0，当且仅当2x+lnx=0时，等号成立. x e2x+lnx −(2x+lnx)−1 （ ） =0，|a|−1=0，−1a1.故选D. x min 二、多选题 9 10 11 ACD ABD BD 11．解：令x =0，y=1，则 f(1)− f(0) f(1)=0，又 f(1)0，f(0)=1，故A错误； 令x=1，y=−1，则 f(0)− f(1) f(−1)=1，f(1) f(−1)=0，又 f(1)0， f(−1)=0，再令y=−1， f(x−1)− f(x) f(−1)= x，f(x−1)= x， f(x)= x+1， f(x)的图象关于(−1,0)中心对称，故B正确； 由B得 f(x)= x+1，当x =0时，ex = x+1，故C错误； 1 由B得 f(x)= x+1，y =−xf(x)=−x2 −x,在x=− 时取到最大值，故D正确. 2 三、填空题 e 12. 1; 13. 4+2 3； 14. 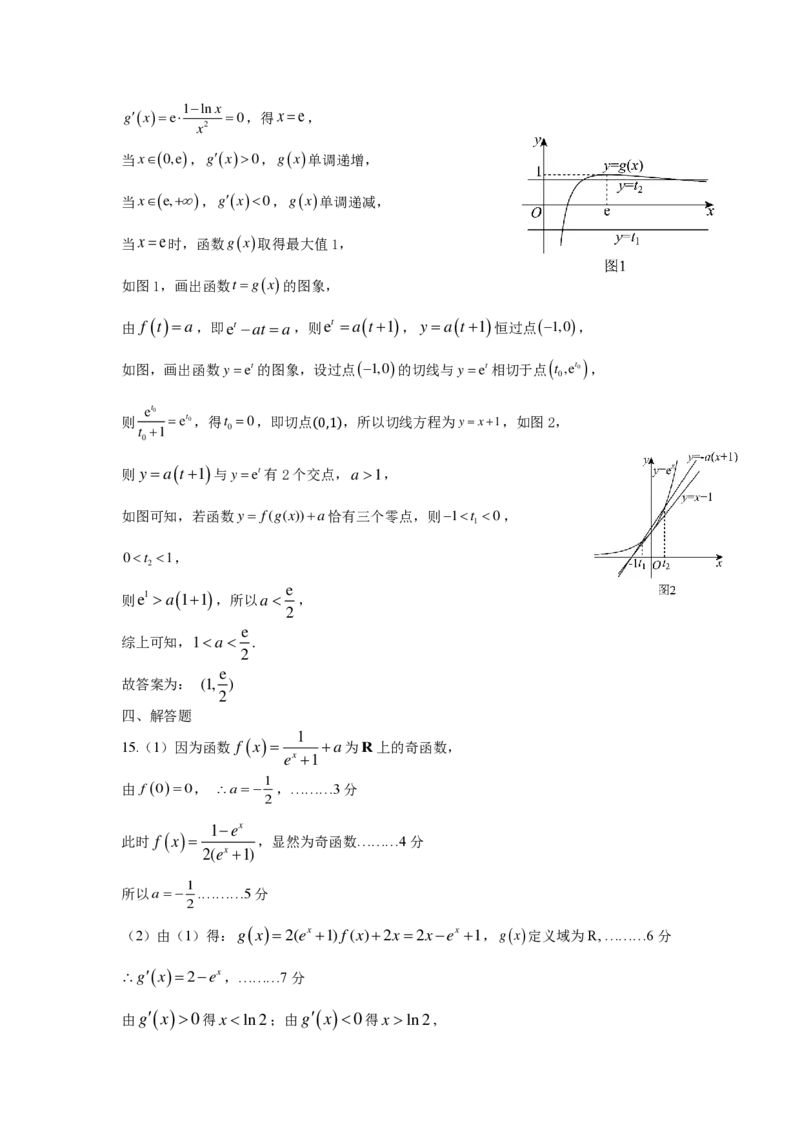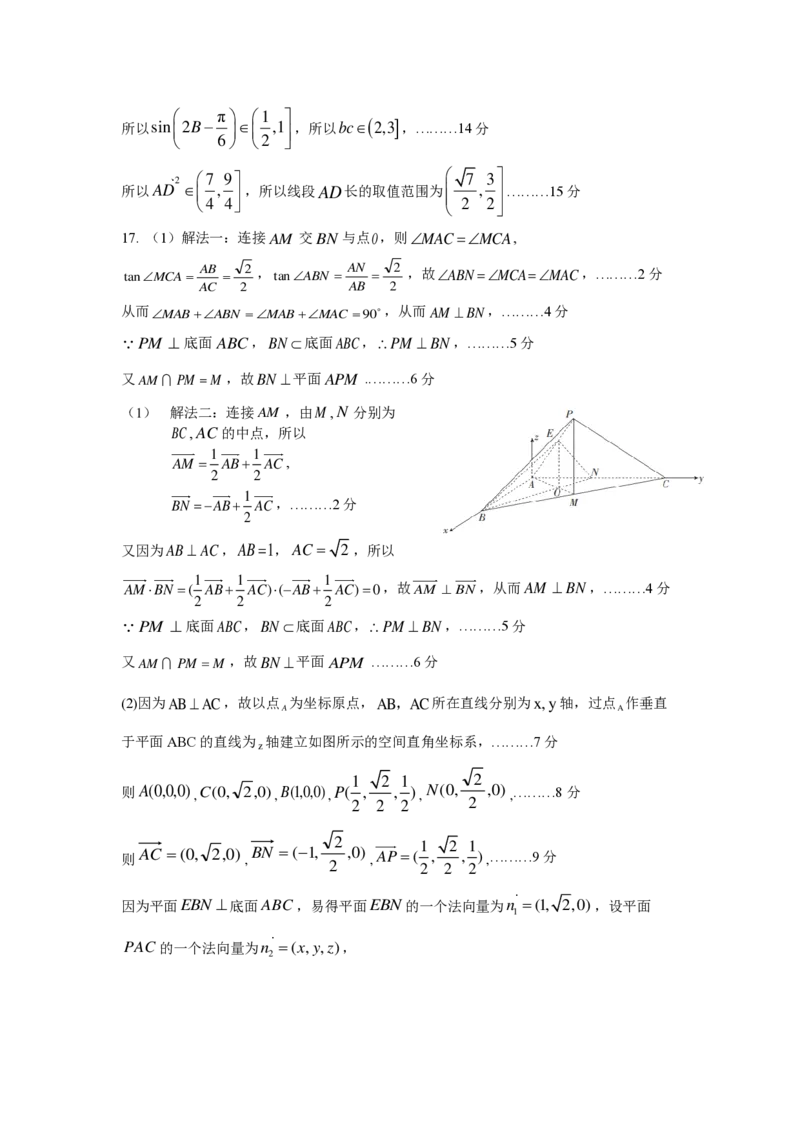(1, ) 2 14．解：设g(x)=t，则 f (t)=a，1−lnx g(x)=e =0，得x=e， x2 当x(0,e)，g(x)0，g(x)单调递增， 当x(e,+)，g(x)0，g(x)单调递减， 当x=e时，函数g(x)取得最大值1， 如图1，画出函数t=g(x)的图象， 由 f (t)=a，即et −at =a，则et =a(t+1) ，y=a(t+1) 恒过点(−1,0)， 如图，画出函数y=et的图象，设过点(−1,0)的切线与y=et相切于点 ( t ,et0 ) ， 0 et0 则 =et0，得t =0，即切点(0,1)，所以切线方程为y=x+1，如图2， t +1 0 0 则y=a(t+1) 与y=et有2个交点，a1， 如图可知，若函数y= f(g(x))+a恰有三个零点，则−1t 0， 1 0t 1， 2 e 则e1 a(1+1) ，所以a ， 2 e 综上可知，1a . 2 e 故答案为： (1, ) 2 四、解答题 1 15.（1）因为函数 f (x)= +a为R上的奇函数， ex +1 1 由 f (0)=0， a=− ，………3分 2 1−ex 此时 f (x)= ，显然为奇函数………4分 2(ex +1) 1 所以a=− .………5分 2 （2）由（1）得：g(x)=2(ex +1)f(x)+2x=2x−ex +1，g(x)定义域为R, ………6分 g(x)=2−ex，………7分 由g(x)0得xln2；由g(x)0得x ln2,g(x) 在 (−,ln2) 上单调递增，g(x) 在 (ln2，+) 上单调递减，………10分 所以g(x) 在x =ln2处取得极大值， f (x) =f (ln2)=2ln2−1；无极小值.………13分 极大值 （不写无极小值扣1分） 2 3c2 16. （1）因为tanA+tanB= ，由余弦定理得 a2 +c2 −b2 2 3c2 3c 3sinC tanA+tanB= = = ，………2分 2accosB acosB sinAcosB 由正弦定理得 sinC sinA sinB sinAcosB+sinBcosA sin(A+B) sinC tanA+tanB= = + = = = ， sinAcosB cosA cosB cosAcosB cosAcosB cosAcosB ………4分 又 ABC是锐角三角形，所以sinC0,cosB0， 所以sinA= 3cosA，所以tanA= 3，  π π 又A0, ，所以A= ．………6分  2 3 （2）由余弦定理可得a2 =c2 +b2 −2cbcosA=c2 +b2 −cb=3，………7分 1( ) 又AD= AB+AC ，所以 2 AD 2 = 1 (AB+ AC)2 = 1( AB 2 + AC 2 +2ABAC ) = 1 ( c2 +b2 +bc ) 4 4 4 1 3 1 = (3+2bc)= + bc，………9分 4 4 2 a b c 由正弦定理可得 = = =2，所以b=2sinB， sinA sinB sinC 2π  3 1 c=2sinC =2sin  −B  =2( cosB+ sinB)，………11分  3  2 2 所以  3 1   3 1 1−cos2B  π bc=4  sinBcosB+ sin2B  =4  sin2B+    =2sin  2B−  +1，…12分  2 2   4 2 2   6  π 0B ,   2 π π π π 5π 由题意得 解得 B ，则2B−   , ，………13分 0 2π −B π , 6 2 6 6 6   3 2 π 1  所以sin  2B−    ,1  ，所以bc(2,3 ，………14分  6 2  2 7 9  7 3 所以AD   ,  ，所以线段AD长的取值范围为  , ………15分 4 4  2 2  17. （1）解法一：连接AM 交BN 与点O，则MAC=MCA, AB 2 AN 2 tanMCA= = ，tanABN = = ，故ABN=MCA=MAC，………2分 AC 2 AB 2 从而MAB+ABN =MAB+MAC =90，从而AM ⊥BN，………4分 PM ⊥ 底面 ABC，BN 底面ABC，PM ⊥BN，………5分 又AM  PM =M ，故BN ⊥平面 APM .………6分 （1） 解法二：连接AM ，由M,N 分别为 BC,AC 的中点，所以 1 1 AM = AB+ AC, 2 2 1 BN =−AB+ AC，………2分 2 又因为AB⊥ AC，AB=1，AC = 2 ，所以 1 1 1 AMBN =( AB+ AC)(−AB+ AC)=0，故AM ⊥ BN，从而AM ⊥BN，………4分 2 2 2 PM ⊥ 底面ABC，BN 底面ABC，PM ⊥BN，………5分 又AM  PM =M ，故BN ⊥平面 APM ………6分 (2)因为AB⊥AC，故以点 为坐标原点，AB，AC所在直线分别为x,y轴，过点 作垂直 A A 于平面ABC的直线为 轴建立如图所示的空间直角坐标系，………7分 z 1 2 1 2 则 A(0,0,0) ,C(0, 2,0), B(1,0,0) , P( , , ) , N(0, ,0) ,………8分 2 2 2 2 2 1 2 1 则 AC =(0, 2,0) , BN =(−1, ,0) , AP=( , , ) ,………9分 2 2 2 2 因为平面EBN ⊥底面ABC，易得平面EBN的一个法向量为n =(1, 2,0)，设平面 1 PAC 的一个法向量为n =(x,y,z)， 2 1 2 1 APn =0  x+ y+ z =0 则  2 ，可得2 2 2 ，令x=1可得n =(1,0,−1)，………12分 ACn =0 2  2   2y =0 1 6 设二面角A−EN −B为  ，则cos=|cosn,n |= = ， 1 2 3 2 6 ………14分 30 故二面角A−EN −B的正弦值为 .………15分 6 x−2 3−x 18.(1)当a =1时， f(x)= −(3x−1)，则 f(x)= −3，………1分 ex ex 令 f(x)0，解得x0，令 f(x)0 ，解得x 0，………3分 所以 f(x)在(−,0)单调递增，(0,+)单调递减；………4分 (2) 函数 f (x) 的图象是连续的，且在定义域上是单调函数， 3−x 3−x  f(x)= −3a0在定义域内恒成立，或 f(x)= −3a0，在定义域内恒成 ex ex 立. ………5分 x−4 f(x)= 在(−,4)为负，(4,+)为正， ex 3−x 所以 f(x)= −3a在(−,4)单调递减，(4,+)单调递增，………7分 ex 3−x ① 若 f(x)= −3a0在定义域内恒成立， ex 1 1 只需 f(x) = f(4)=− −3a0，即a− .………8分 min e4 3e4 3−x ② 若 f(x)= −3a0在定义域内恒成立， ex x→−时， f(x)→+，故该情况a无解 . ………9分 1 综上：a− ………10分 3e4 . x−2 (3)若 f(x)0恒成立，则 −a(3x−1)−b−10，当x =2时，−5a−b−10，即 ex 5a+b−1，………11分x−2 下证5a+b=−1成立，由5a+1=−b得， −a(3x−1)+5a0恒成立， ex x−2 即 −a(3x−6)0，………12分 ex x−2 记F(x)= −a(3x−6) F(2)=0，故F(2)=0， ex 3−x 1 1 而F(x)= −3a，则 −3a=0，解得a = ，………14分 ex e2 3e2 x−2 1 只需证F(x)= − (3x−6)0恒成立， ex 3e2 3−x 1 F(x)= − ，由（2）得F(x)在(−,4)上单调递减，在(4,+)上单调递增， ex e2 又F(2)=0，F(x)在(−,2)上为正，在(2,4)上为负，在(4,+)上为负， F(x)在(−,2)上单调递增，在(2,+)上单调递减，F(x) = F(2)=0， max 即F(x)0恒成立，………16分 5a+b最小值为−1. ………17分  19.解：（1） f(x)图象的相邻的两条对称轴间的距离为 2  2  f(x)的最小正周期为T=2 = 0，= =2，………1分 2 T  3 3 f(x)=sin(2x+)又 f(x)的图象过点0, ， f(0)=sin= .   2 2       ，= ，f(x)=sin(2x+ )………2分 2 3 3  因为函数y = f(x+m)=sin(2x+2m+ )是偶函数 3    k 2m+ =k+ (kZ)，m= + (kZ)………3分 3 2 12 2  |m|的最小值 .………4分 12   1 （2）由g(x)=4f(x)+1=4sin(2x+ )+1=0可得sin(2x+ )=− ………5分 3 3 4  17 31   5 11 x − , ，2x+  − , ………6分      12 12  3  2 2   1  5 11 设2x + =t ，由y=sint与y =− 图象可知在 − , 共有8个交点………7分 i 3 i 4   2 2  8 6 4 2 4π 3π 2π π π 2π 3π 4π 5π 6π 2 t +t =t +t =4 t +t =t +t =3………8分 1 8 2 7 3 6 4 5 6   7 2x + +2x + 8 =3,x +x = ，同理2x +2x +2x +2x +2x +2x =7, 1 3 8 3 1 8 6 2 3 4 5 6 7 ………9分 49 x +2x +2x +2x +2x +2x +2x +x = .………10分 1 2 3 4 5 6 7 8 6  1 x  1 x （3） f(x)=sin(2x+ )，h(x)=   f(x− )=   sin(2x)………11分 3 2 6 2 x 1 假设存在非零实数，使得函数h(x)=   sin2x是R上的周期为T的T级周期函数， 2 即xR，恒有h(x+T)=Th(x)， x+T x 1 1 则xR，恒有 sin(2x+2T)=T sin2x成立，     2 2 则xR，恒有sin(2x+2T)=T2T sin2x成立，………13分 当0时，xR，则2xR，2x+2TR， 所以，−1sin2x1，−1sin(2x+2T)1， 要使得sin(2x+2T)=T2T sin2x恒成立，则有T 2T =1.………14分 1 1 当T 2T =1时，则T 0，即2T = ，令p(x)=2x− ，其中x0， T x 1 则p = 2−20，p(1)=2−1=10， 2 且函数p(x)在(0,+)上的图象是连续的， 由零点存在定理可知，函数p(x)在(0,+)上有唯一的零点，此时，sin(2x+2T)=sin2x恒成立，则2T =2mπ(mZ) ，即 mπ = (mZ)；………15分 T 当T 2T =−1时，则T 0，即−T =2−T，作出函数y=−x、 y=2−x的图象如下图所示： 由图可知，函数y=−x、y=2−x的图象没有公共点， 故方程T 2T =−1无实数解. ………16分 mπ 综上所述，存在= (mZ)满足题意，其中T满足T 2T =1.………17分 T