文档内容
2024 届高三第三次校际联考
数学(文科)试题
注意事项:
1.本试题共4页,满分150分,时间120分钟.
2.答卷前,务必将答题卡上密封线内的各项目填写清楚.
3.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改
动,用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上.写在本试
卷上无效.
4.考试结束后,监考员将答题卡按顺序收回,装袋整理;试题不回收.
第Ⅰ卷(选择题 共 60 分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.已知复数z满足 ,则z的虚部为
A. B. C. D.
2.命题“ , ”的否定是
A. , B. ,
C. , D. ,
3.已知全集 ,集合 , ,则
A. B. C. D.
4.双曲线C: 的焦点坐标为
A. B. C. D.
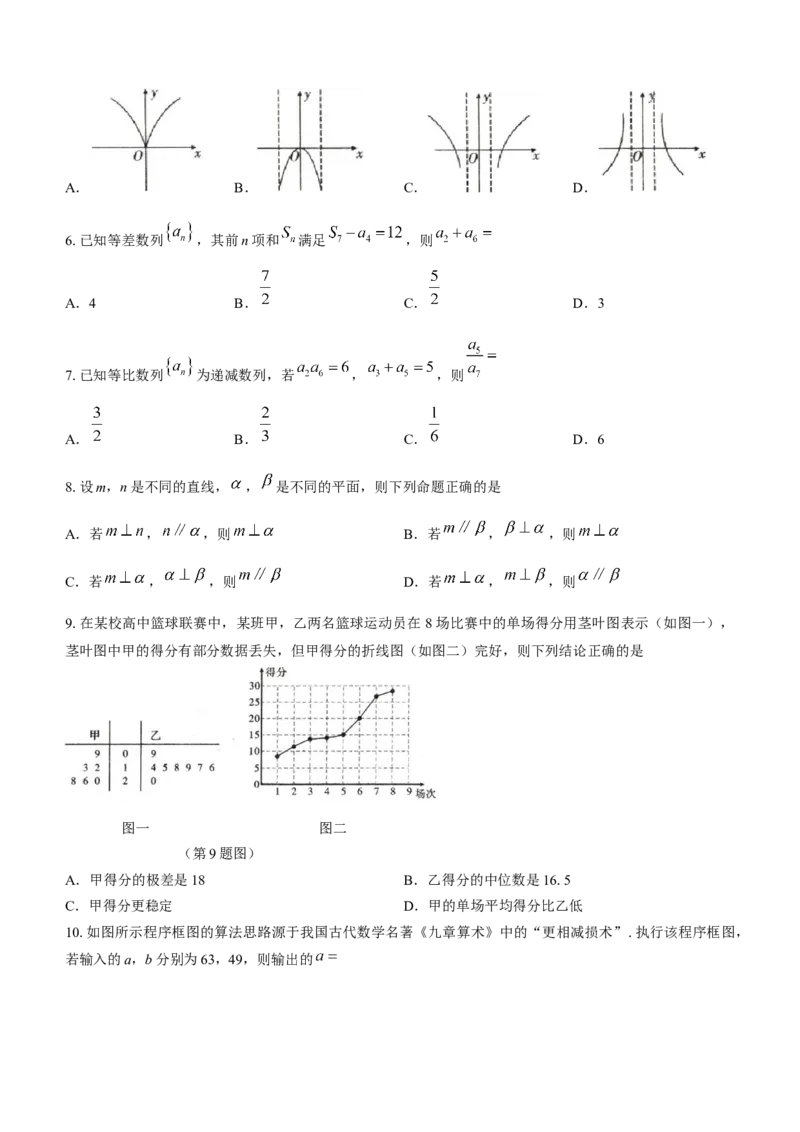
5.若 ,则函数 的图象可以是
学科网(北京)股份有限公司A. B. C. D.
6.已知等差数列 ,其前n项和 满足 ,则
A.4 B. C. D.3
7.已知等比数列 为递减数列,若 , ,则
A. B. C. D.6
8.设m,n是不同的直线, , 是不同的平面,则下列命题正确的是
A.若 , ,则 B.若 , ,则
C.若 , ,则 D.若 , ,则
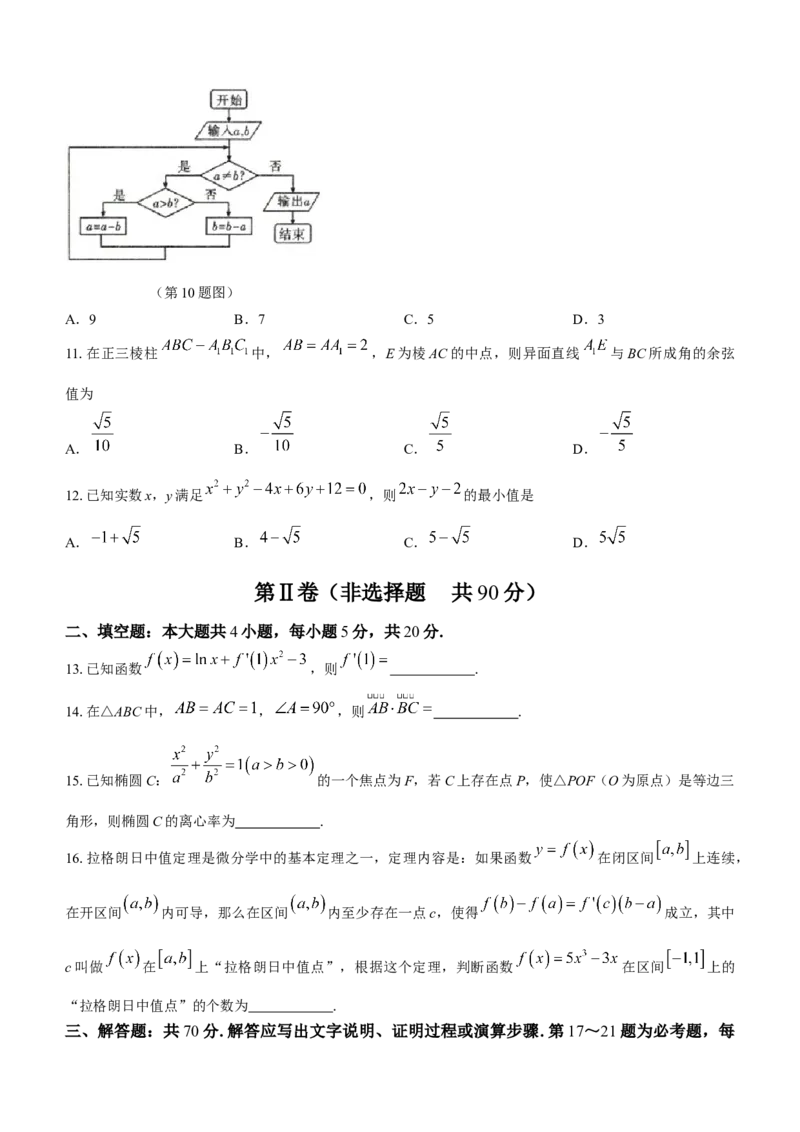
9.在某校高中篮球联赛中,某班甲,乙两名篮球运动员在 8场比赛中的单场得分用茎叶图表示(如图一),
茎叶图中甲的得分有部分数据丢失,但甲得分的折线图(如图二)完好,则下列结论正确的是
图一 图二
(第9题图)
A.甲得分的极差是18 B.乙得分的中位数是16.5
C.甲得分更稳定 D.甲的单场平均得分比乙低
10.如图所示程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,
若输入的a,b分别为63,49,则输出的
学科网(北京)股份有限公司(第10题图)
A.9 B.7 C.5 D.3
11.在正三棱柱 中, ,E为棱AC的中点,则异面直线 与BC所成角的余弦
值为
A. B. C. D.
12.已知实数x,y满足 ,则 的最小值是
A. B. C. D.
第Ⅱ卷(非选择题 共 90 分)
二、填空题:本大题共4小题,每小题5分,共20分.
13.已知函数 ,则 .
14.在△ABC中, , ,则 .
15.已知椭圆C: 的一个焦点为F,若C上存在点P,使△POF(O为原点)是等边三
角形,则椭圆C的离心率为 .
16.拉格朗日中值定理是微分学中的基本定理之一,定理内容是:如果函数 在闭区间 上连续,
在开区间 内可导,那么在区间 内至少存在一点c,使得 成立,其中
c叫做 在 上“拉格朗日中值点”,根据这个定理,判断函数 在区间 上的
“拉格朗日中值点”的个数为 .
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每
学科网(北京)股份有限公司个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(本小题满分12分)
已知△ABC的内角A,B,C的对边分别为a,b,c,且 .
(Ⅰ)求角B;
(Ⅱ)若 , ,求△ABC的面积.
18.(本小题满分12分)
某企业生产的产品按质量分为一等品和二等品,该企业计划对现有生产设备进行改造,为了分析设备改造前
后的效果,现从设备改造前后生产的大量产品中各抽取200件产品作为样本,产品的质量情况统计如表:
一等品 二等品 合计
设备改造前 120 80 200
设备改造后 150 50 200
合计 270 130 400
(Ⅰ)判断是否有99%的把握,认为该企业生产的这种产品的质量与设备改造有关;
(Ⅱ)按照分层抽样的方法,从设备改造前的产品中取得了5件产品,其中有3件一等品和2件二等品.现从
这5件产品中任选2件,求选出的这2件全是一等品的概率.
附: ,其中 .
0.050 0.010 0.001
3.841 6.635 10.828
19.(本小题满分12分)
如图,在三棱锥A-BCD中,△ABD是等边三角形,ABCD是等腰直角三角形,BC⊥CD, ,点O,E
分别为BD,AD的中点.
(第19题图)
(Ⅰ)证明:AC⊥BD;
(Ⅱ)求三棱锥A-EOC的体积.
20.(本小题满分12分)
学科网(北京)股份有限公司已知函数 .
(Ⅰ)若 在 处的切线与x轴平行,求实数a的值;
(Ⅱ) 是否存在极值点,若存在,求出极值点;若不存在,请说明理由.
21.(本小题满分12分)
在平面直角坐标系xOy中,抛物线的方程为 ,其顶点到焦点的距离为2.
(Ⅰ)求抛物线的方程;
(Ⅱ)若点 ,设直线l: 与抛物线交于A、B两点,且直线PA、PB的斜率之和为
0,证明:直线l必过定点,并求出该定点的坐标.
(二)选考题:共10分.考生从22、23题中任选一题作答,如果多做,则按所做的第一题计分.
22.(本小题满分10分)【选修4-4:坐标系与参数方程】
在平面直角坐标系x0y中,直线l的参数方程为 (t为参数).在以原点O为极点,x轴正半轴
为极轴的极坐标系中,圆C的极坐标方程为 .
(Ⅰ)写出直线l的普通方程和圆C的直角坐标方程;
(Ⅱ)若点P的直角坐标为 ,圆C与直线l交于A,B两点,求 的值.
23.(本小题满分10分)【选修4-5:不等式选讲】
已知函数 , .
(Ⅰ)若 ,求不等式 的解集;
(Ⅱ)若 ,求a的取值范围.
2024 届高三第三次校际联考
数学(文科)试题参考答案及评分标准
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项
学科网(北京)股份有限公司是符合题目要求的.
1.B 2.A 3.D 4.D 5.D 6.A 7.A 8.D 9.B 10.B 11.A 12.C
二、填空题:本大题共4小题,每小题5分,共20分.
13. 14. 15. 16.2
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每
个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.解:
(Ⅰ)∵ ,
∴由正弦定理可得 ,
又 ,∴ ,即 ,
∵ ,
∴ .
(Ⅱ)∵ , , ,
∴由余弦定理可得 ,即 ,
解得 ,即 , ,
∴ .
18.解:
(Ⅰ)∵ ,
∴有99%的把握认为该企业生产的这种产品的质量与设备改造有关.
(Ⅱ)在取出的5件产品中,3件一等品记为a,b,c,2件二等品记为D,E,
从这5件产品中任选2件的所有情况为ab,ac,aD,aE,bc,bD,bE,cD,cE,DE,共10种,
其中2件全是一等品的情况为ab,ac,bc,共3种,
学科网(北京)股份有限公司∴选出的2件全是一等品的概率为 .
19.解:
(Ⅰ)证明:∵△ABD是等边三角形,点O为BD中点,
∴ .
又∵ ,
∴ .
又∵ ,
∴ 平面AOC.
又∵ 平面AOC,
∴ .
(Ⅱ)由题意知 , ,
∴ .
由(Ⅰ)知 平面AOC,
又点E为AD中点,
∴点E到平面AOC的距离为 .
∴ .
20.解:
(Ⅰ)由 ,得 ,
∵ 在 处的切线与x轴平行,
∴ ,解得 .
(Ⅱ)函数 的定义域为 , .
学科网(北京)股份有限公司当 时,对任意的 , ,此时函数 无极值点;
当 时,令 ,可得 ,
由 ,可得 ;由 ,可得 .
此时,函数 的减区间为 ,增区间为 .
∴函数 在 处取得极小值.
综上,
当 时,函数 无极值点;
当 时,函数 的极小值点为 ,无极大值点.
21.解:
(Ⅰ)∵抛物线 的顶点到焦点的距离为2,
∴ ,解得 .
∴该抛物线的方程为 .
(Ⅱ)证明:设点 、 ,
把直线 代入 ,消去y,整理得 ,
则 且 , ,
直线PA的斜率为 ,
同理得直线PB的斜率 ,
则 ,
学科网(北京)股份有限公司即 ,显然 ,故 ,
∴直线l的方程为 ,故直线l必过定点 .
(二)选考题:共10分.考生从22、23题中任选一题作答,如果多做,则按所做的第一题计分.
22.解:
(Ⅰ)由直线l的参数为 (t为参数),
得直线l的普通方程为 .
将圆C的极坐标方程: 两边同乘 得 ,
化为直角坐标方程为 .
(Ⅱ)把直线l的参数方程代入圆C的直角坐标方程,
得 ,即 ,
设 , 是A和B对应的参数,
则 , ,
又直线l过点 ,
∴ .
23.解:
(Ⅰ)当 时, ,
当 时,不等式 化为 ,
∴ ,此时 ;
当 时,不等式 化为 ,恒成立,此时 ;
当 时,不等式 化为 ,
学科网(北京)股份有限公司∴ ,此时 .
综上所述,不等式 的解集为 .
(Ⅱ) ,
若 ,则 ,
不等式两边平方可得 ,解得 ,
又 ,
∴ ,
即a的取值范围是 .
学科网(北京)股份有限公司