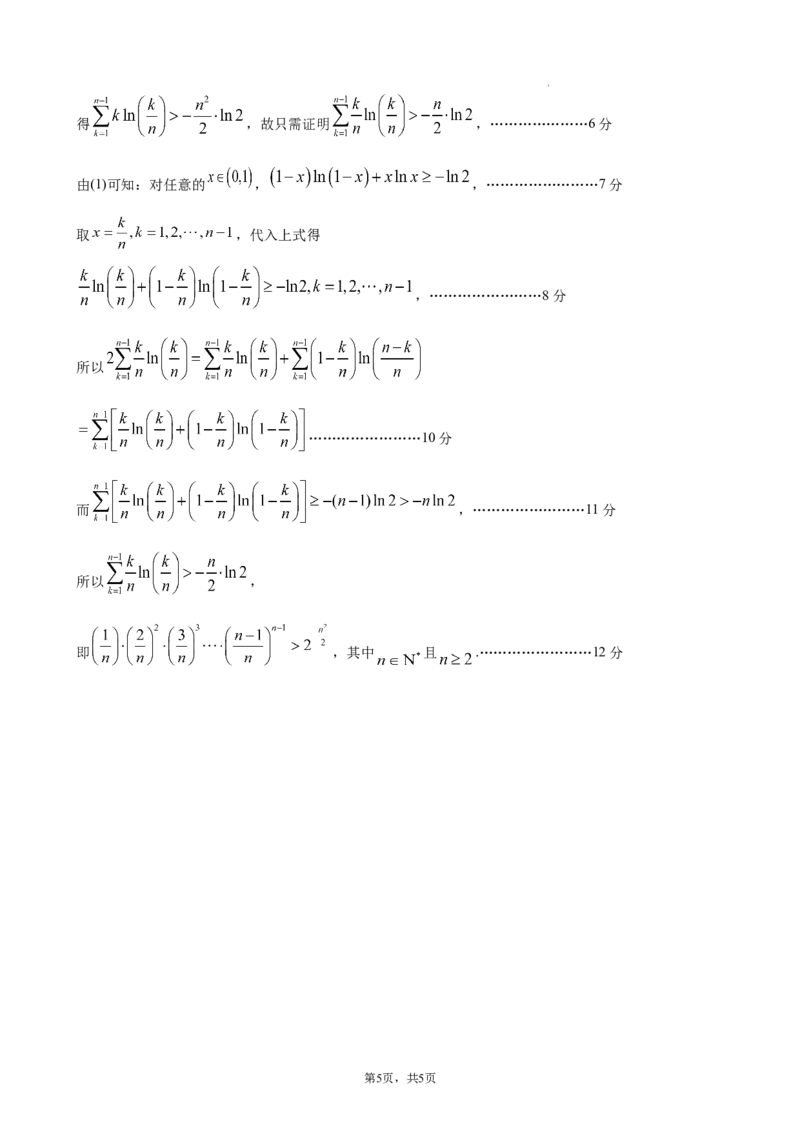文档内容
(高三数学)参考答案
一、单项选择题
1-4 DBAC 5-8 DCAA
二、多项选择题
9.BC 10.BCD 11.ACD 12.AC
三、填空题
13.2 14.8 15. 16.
四、解答题
17.解:(1)设等差数列 的公差为d,因为 , ,
所以 ,解得 ,……………………3分
所以 ,即数列 的通项公式为 ;……………………5分
(2)因为 ,……………………8分
所以 .
所以数列 的前n项和 .……………………10分
18.解:(1)由题设及正弦定理得 ,……………………2分
所以 ,故 ,……………………4分
因为 ,所以 .……………………6分
(2)由题设及(1)知△ABC的面积 .
由正弦定理得 .……………………8分
由于△ABC为锐角三角形,故 , .
由(1)知 ,所以 ,……………………10分
故 ,从而 .
第1页,共5页
学科网(北京)股份有限公司3 3
( , )
因此,△ABC面积的取值范围是 8 2 .……………………………12分
19.解:(1)曲线 与曲线 的公共点坐标为 . ………………2分
因为 , 所以 , ……………………4分
所以曲线 在公共点处的切线方程为 ,
即 . ……………………6分
(2)因为直线 分别交曲线 和 于点A,B.
所以A ,B .
, . ……………………8分
因为 时, ,所以 ,
所以 , , , ……………………10分
令 ,得 ,
所以 的情况如下:
0
极大值
因此, 的极大值,也是最大值为 . ……………………………12分
20.解:(1)由已知得 ,
所以 ,……………………2分
因为 , ,所以 ,……………………3分
所以 是以 为首项, 为公比的等比数列,……………………4分
所以 , ,
所以 的通项公式 ;……………………6分
第2页,共5页
学科网(北京)股份有限公司(2)由 知 ,
所以 ,……………………7分
所以
,……………………9分
当 时,
令 ,可知 且当 时, 单调递增,
所以当 时, ,即当 时, .…………………………12分
21.解:(1)由抛物线 的顶点在原点,对称轴为坐标轴可知,
点 和点 不可能同时在抛物线 上,点 和点 不可能同时在抛物线 上,点
和点 也不可能同时在抛物线 上,
所以抛物线 过 , 两点.……………………3分
设 ,代入点 ,则 ,得 ,
所以 ,抛物线过点 ,满足题意.
综上,抛物线 的方程为 .……………………5分
(2)设直线 , ,
根据题意可知: ,且 ,
联立 ,得 ,则 ,
第3页,共5页
学科网(北京)股份有限公司同理联立 ,得 ,则 ,……………………7分
由 得 ,即 ,
所以 ,
即 ,整理得 ……………………8分
又因为 ,所以 ,……………………9分
由 ,得
联立 ,所以 ,……………………11分
故 .……………………………12分
22.解:(1)由题可知对任意的 , 恒成立,
令 ,则 ,……………………2分
令 得 ,且 ,
所以 在 上递减,在 上递增,
所以 在 上的最小值为 ,……………………4分
由题可知 ,所以 ,
所以t的取值范围为 .……………………5分
(2)要证不等式 两边取对数,
第4页,共5页
学科网(北京)股份有限公司得 ,故只需证明 ,…………………6分
由(1)可知:对任意的 , ,……………………7分
取 ,代入上式得
,……………………8分
所以
……………………10分
而 ,……………………11分
所以 ,
即 ,其中 且 .……………………12分
第5页,共5页
学科网(北京)股份有限公司