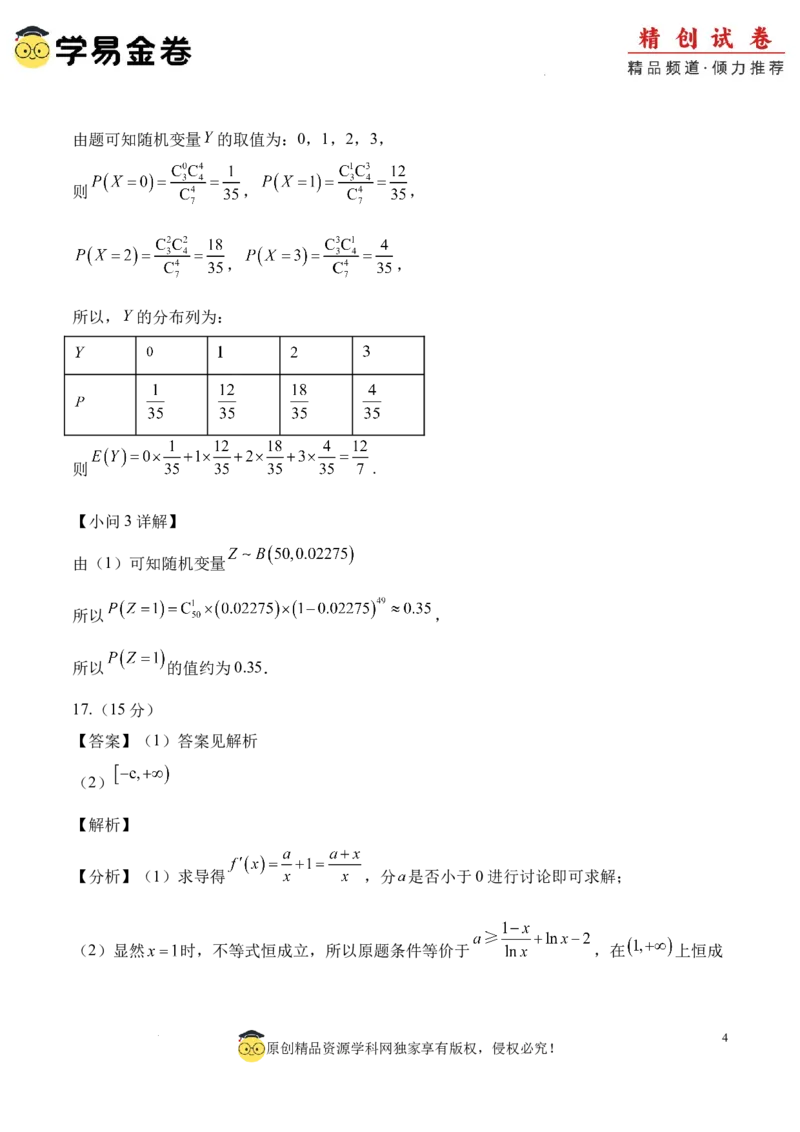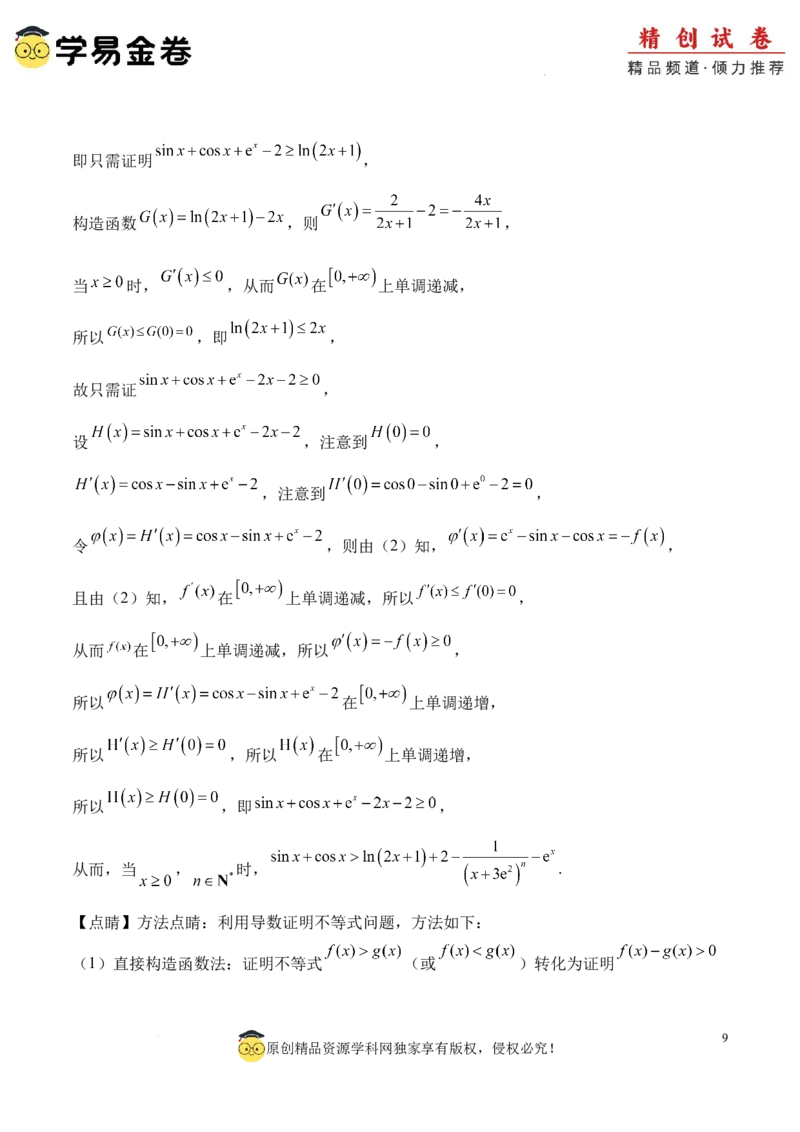文档内容
2023-2024 学年高二年级数学下学期期末模拟卷
数学·参考答案
第Ⅰ卷
选择题:本大题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项
一、
中,只有一项是符合题目要求的.
1 2 3 4 5 6 7 8
D A B D A C C B
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,
有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0
分.
9 10 11
AC ABD ABC
第Ⅱ卷
三、填空题:本题共3小题,每小题5分,共15分.
12.3
13.
14.
三、解答题(本大题共8个小题,共75分.解答应写出文字说明,证明过程或演算步骤)
15.(13分)【答案】(1)
1
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司(2)
【解析】
【分析】(1)根据等比数列基本量的计算可得 , ,即可求解公比得解,
.
(2)利用错位相减法求和即可求解
【小问1详解】
由 以及 可得 ,
又 ,故 ,
因此公比 ,
故
【小问2详解】
,
则 ,
,
两式相减可得 ,
,
2
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司,
.
16.(15分)
【答案】(1)
(2)分布列见解析;期望为
(3)0.35
【解析】
【分析】(1)由题意 ,利用 原则可求解;
(2)利用超几何分布的概率公式求分布列,进而得到期望;
(3)由二项分布可求.
【小问1详解】
因为该市人口数量在950万人左右的社区这一天的垃圾量 大致服从正态分布 ,
所以 ,
因为 ,
所以这 个社区中“超标”社区的个数为 .
【小问2详解】
3
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司由题可知随机变量 的取值为:0,1,2,3,
则 , ,
, ,
所以, 的分布列为:
则 .
【小问3详解】
由(1)可知随机变量
所以 ,
所以 的值约为0.35.
17.(15分)
【答案】(1)答案见解析
(2)
【解析】
【分析】(1)求导得 ,分 是否小于0进行讨论即可求解;
(2)显然 时,不等式恒成立,所以原题条件等价于 ,在 上恒成
4
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司立,构造函数 , ,利用导数求得其最大值即可得解.
【小问1详解】
的定义域为 , ,
当 时, ,所以 在 上单调递增;
当 时,当 时, ,当 时, ,
所以 在 上单调递减,在 上单调递增.
【小问2详解】
当 时, 显然成立,此时 可为任意实数;
当 时,由 , 在 上恒成立,得 ,
令 , ,
则 ,
设 ,由(1)可知, 在 上单调递增,所以 ,
当 时, ,当 时, ,
所以 在 上单调递增,在 上单调递减;
则 ,所以 ,
5
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司综上,实数 的取值范围为 .
18.(17分)
【答案】(1)模型②,
(2)认为该地区对职业结构变化的自信程度与年龄有关
【解析】
【分析】(1)根据数据分析,函数和一次函数模型差距较大,选择模型②: . 然
后结合线性回归分析,求得函数 ;
(2)列联表,计算卡方,然后对比 的数据,做出判断即可;
【小问1详解】
选择模型②: .
记 ,则 .
由题知, , , , ,
所以 , ,
所以 ,即y关于x的回归方程为 .
【小问2详解】
由题意,得到列联表:
基本适应 不适应 合计
年龄不小于30岁 75 75 150
年龄小于30岁 100 50 150
6
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司合计 175 125 300
,
根据 的独立性检验,认为该地区对职业结构变化的自信程度与年龄有关,此推断犯
错误的概率不大于0.01.
(17分)
【答案】(1)图象见解析,存在“自公切线”
(2)证明见解析 (3)证明见解析
【解析】
【分析】(1)将曲线C: 方程变形,由圆的函数图象作出其图象,结合
“自公切线”定义即可判断.
(2)结合“自公切线”定义将所证不等式转化为证明 在 上单调即可,构造函数,
利用导数研究其单调性,即可证明.
(3)根据 将所证不等式转化为证明 ,构造函数
,利用导数研究其最值证明 ,进一步转化为证明
,,设 ,求导,利用(2)的结论,
得 在 上单调递增,即可证明.
【小问1详解】
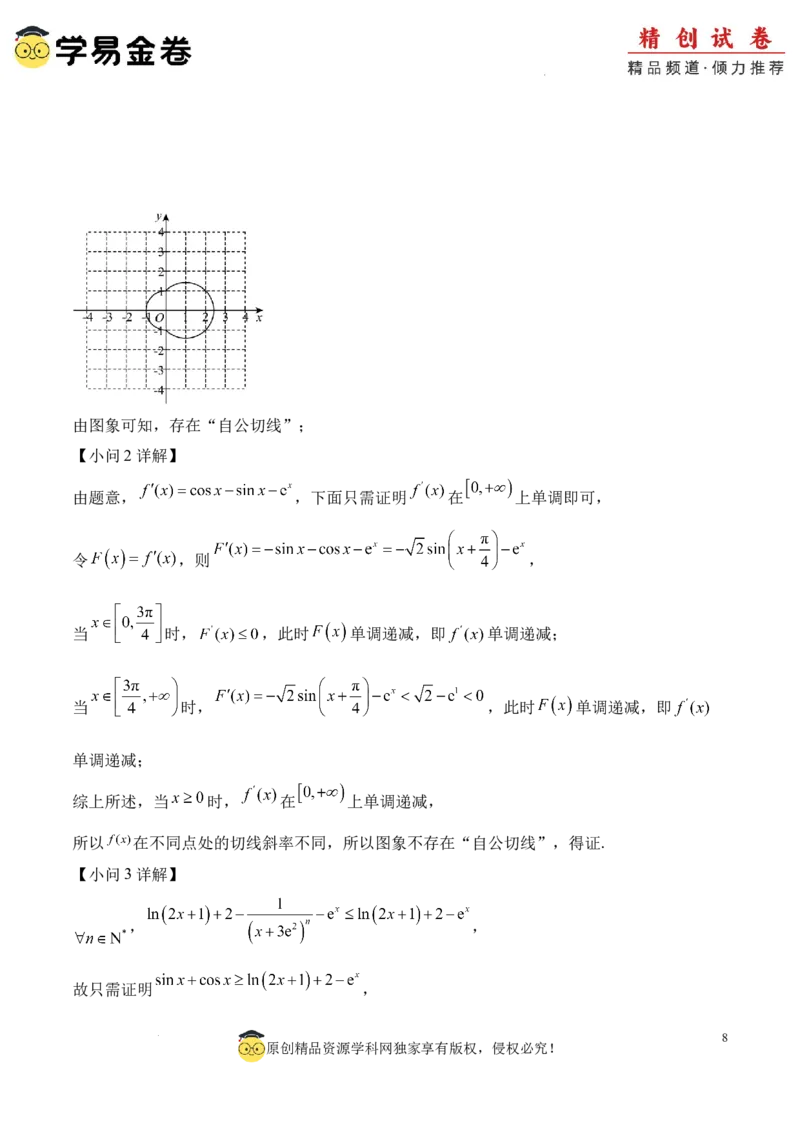
曲线C: ,当 时, ,表示以点 为圆心,半径为
的部分圆弧,当 时, ,表示以点 为圆心,半径为 的半圆圆,从而
图象如下:
7
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司由图象可知,存在“自公切线”;
【小问2详解】
由题意, ,下面只需证明 在 上单调即可,
令 ,则 ,
当 时, ,此时 单调递减,即 单调递减;
当 时, ,此时 单调递减,即
单调递减;
综上所述,当 时, 在 上单调递减,
所以 在不同点处的切线斜率不同,所以图象不存在“自公切线”,得证.
【小问3详解】
, ,
故只需证明 ,
8
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司即只需证明 ,
构造函数 ,则 ,
当 时, ,从而 在 上单调递减,
所以 ,即 ,
故只需证 ,
设 ,注意到 ,
,注意到 ,
令 ,则由(2)知, ,
且由(2)知, 在 上单调递减,所以 ,
从而 在 上单调递减,所以 ,
所以 在 上单调递增,
所以 ,所以 在 上单调递增,
所以 ,即 ,
从而,当 , 时, .
【点睛】方法点睛:利用导数证明不等式问题,方法如下:
(1)直接构造函数法:证明不等式 (或 )转化为证明
9
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司(或 ),进而构造辅助函数 ;
(2)适当放缩构造法:一是根据已知条件适当放缩;二是利用常见放缩结论;
(3)构造“形似”函数,稍作变形再构造,对原不等式同解变形,根据相似结构构造辅助函
数.
10
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司