高三数学答案(1)_2023年11月_0211月合集_2024届辽宁省辽西联合校高三上学期期中考试_辽宁省辽西联合校2024届高三上学期期中考试数学

2023-2024 学年度上学期辽西联合校高三期中考试 （数学参考答案，提示及评分细则） 参考答案： 1．A 【详解】由   ，而A{1,3}， C B  3,5 U 所以  . C B A 1,3,5 U 故选：A 2．C 【详解】命题“xN,5x x31”的否定是“xN,5x x3 1”. 故选：C 3．C   【详解】由E为AC边上的点，且AE3EC，    1  1  1  1    1  1  得ED ECCD AC CB AC CA AB  AB AC. 4 2 4 2 2 4 故选：C 4．C 【详解】由 x2m 1，即1x2m1，解得2m1x12m， 因为“1x2”是“ x2m 1”充分不必要条件， 12m2 1 所以1,2真包含于2m1,12m，所以 （等号不能同时取得），解得 m1， 2m11 2 1  所以实数m的取值范围为  ,1 . 2  故选：C 5．A 【详解】∵alog 5log 31，blog 2log 10，0c50.2 50 1， 3 3 0.5 0.5 ∴acb. 故选：A. 6．A 答案第1页，共9页 {#{QQABIYaQggggQAIAAAhCUwFiCgAQkBCCAKoORBAAsAABAANABAA=}#}【详解】解：因为关于x的不等式ax2bxc0a0的解集为3,1， b c 所以a0，且31 ，31 ， a a 所以b2a，c3a， 所以cx2bxa0化为3x22x10， 1 解得  x1. 3 故选：A. 7．B 1 【详解】因为函数 f x为奇函数，且在区间0,上是增函数，且 f  0， 2 1  1 所以函数在(,0)上单调递增且 f  f 0， 2  2 1 1 1 1 所以当x 或0 x 时， f(x)0，当  x0或x 时， f(x)0， 2 2 2 2 f(x) f(x) 2f(x) f x 由 0，即 0，故 0 x x x f x x0 x0 由 0可得 或 ， x f(x)0 f(x)0 1 1 所以  x0或0 x ， 2 2 故选：B 8．D f(x)1 【详解】设g(x) ， ex  f(x) f(x)1，即 f(x) f(x)10， f(x) f(x)1 g(x) 0， ex g(x)在R上单调递减，又 f(0)2023， f(x)1 f(0)1 不等式exf(x)ex2022 2022 f(0)1 ， ex e0 即g(x)g(0)，x0， 原不等式的解集为(,0). 故选：D 9．ABD 【详解】设zabi，则zabi， 由z2z6i， 可得z2z 3abi6i， 3a6, 所以 解得a2,b1，因此z2i，A正确； b1, 答案第2页，共9页 {#{QQABIYaQggggQAIAAAhCUwFiCgAQkBCCAKoORBAAsAABAANABAA=}#}z 2i 2i12i    i，为纯虚数，B正确； 12i 12i 5 z  5，C错误； z2i，其在复平面内对应的点为 ( 2,-1 ) ，在第四象限，D正确． 故选:ABD． 10．ABD r  a 2,1 2 5 5 【详解】对A，与向量a共线且方向相同单位向量为 r    ,   ，故A正确. a 2212  5 5  r    对B，因为a2,1，b3,1，故ab1,2， r r r r r r     故 ab a1220，故 ab a成立，故B正确.     ab 2311 10 对C，向量a在向量b上的投影数量是    ，故C错误. b 32 12 2 r r   对D，a2b2,123,1 4,3，故 a2b  42 32 5，故D正确. 故选：ABD. 11．BC 【详解】因为x0,y0,x y2， 所以2xy2 xy，故 xy 1，当且仅当x y时，取得等号， 所以 xy的最大值为1，故A正确； 1 3 1 9 5 当x ,y 时，x2y2    2，故B错误； 2 2 4 4 2  2 因为 x y xy 2 xy  2 2 xy  2 2 4 ， 所以 x y 2，当且仅当x y时，取得等号， 即 x y 有最大值为2，故C错误； 2 2xy x y  2 因为 1 1  x y  xy   2    1 ，当且仅当x y时，取得等号，  x y 2 所以 1 1 有最大值为1，故D正确；  x y 故选：BC． 12．AD 答案第3页，共9页 {#{QQABIYaQggggQAIAAAhCUwFiCgAQkBCCAKoORBAAsAABAANABAA=}#}1 2π π π 【详解】由函数的图象可得A2，由    ，求得2. 4  3 12 π π 再根据五点法作图可得2 2kππ，即2kπ ,kZ， 3 3 π π  π 又 ，求得 ，∴函数 f x2sin2x ， 2 3  3  5π π f  2sin 2，是最值，故A成立；  12 2 2π 5π π f  2sin 2sin  3，不等于零，故B不成立；  3  3 3  π π 将函数y 3sin2xcos2x2sin 2x 的图象向左平移 个单位得到函数  6 2   π π  5π ysin2x   sin2x  的图象，故C不成立；   2 6  6   π  π  2π π 当x  ,0 时，2x   , ，      2  3  3 3  π  2π   π   5π  π f  2sin 2sin  3， f    2sin    2 ，  2  3   3  12  2  π  函数 f x在  ,0 上的图象如下，    2  由图可知，m  2, 3时，函数 f x与直线ym有两个交点，  故方程 f xm在    π ,0   上有两个不相等的实数根时，m的取值范围是  2, 3  ，故D成立.  2  故选：AD. 1 13． /0.5 2 【详解】因为 f 12，所以 f  f 1  f(2) 1 ， 2 1 故答案为： . 2 14．1,1  1,3 答案第4页，共9页 {#{QQABIYaQggggQAIAAAhCUwFiCgAQkBCCAKoORBAAsAABAANABAA=}#}2x3x2 0 【详解】由 ， x10 1 x3 解得 ， x1 所以函数的定义域为1,1  1,3 故答案为：1,1  1,3 93 15． 16 13 13 a a  2a 【详解】由题意可知， S 13  2 1 13  2 7  a 7， T 13 13 b b  13 2b b 7 2 1 13 2 7 a S 7132 93 所以 7  13   . b T 133 16 7 13 93 故答案为: . 16 16．[8,0] 【详解】命题“x R，ax2ax 20”是假命题， 0 0 0 命题的否定：“xR，ax2ax20”是真命题， 即ax2ax20恒成立， 当a0时，显然成立； a0 当a0时，则 ， a2 8a0 解得：8a0 综上，实数a的取值范围是[8,0]， 故答案为：[8,0]. 17．(1)a  2n 7 ； n (2)S n2 6n，S 的最小值为9. n n 【详解】（1）设等差数列a 的公差为d，由a  5，3a a 0， n 1 3 5 得3(52d)(54d)0，.........................................................................................................................2分 解得d 2， .....................................................................................................................................................3分 于是a a (n1)d 2n7，.所以数列a 的通项公式是a  2n7...............................................5分 n 1 n n a a 5(2n7) （2）由（1）知，S  1 n n nn2 6n ，...................................................................7分 n 2 2 答案第5页，共9页 {#{QQABIYaQggggQAIAAAhCUwFiCgAQkBCCAKoORBAAsAABAANABAA=}#}显然S (n3)2 99，当且仅当n3时取等号，.................................................................................8分 n 所以S n2 6n，S 的最小值为9...............................................................................................................10分 n n 18．(1)AB x 2 x5  ， ð A  B{x|x2或x2} R (2)m2或1m2 【详解】（1）∵A x 2 x5  ，B x m1 x2m1  ， ∴当m3时，则B x 2 x7  ，所以AB x 2 x5  ，...........................................................2分 ð A{x|x2或x5}，............................................................................................................................3分 R 又B x 2 x7  ， 所以 ð A  B{x|x2或x2}............................................................................................................5分 R （2）∵AB A， ∴BA， ∴当B时，则有m12m1，即m2，满足题意；................................................................7分 当B时，则有m12m1，即m2，......................................................................................8分 m12 可得 ，解得：1m2.........................................................................................................10分 2m15 综上所述，m的范围为m2或1m2...........................................................................................12分 19．(1)减区间为(0,2)，增区间为(2,)，极小值为2ln2，无极大值 (2)a1 【详解】（1）函数 f x的定义域为0,，.......................................................................................1分 1 当a1时， f x x2x2lnx 2 2 x2x1 求导得 fxx1 ，整理得： fx .....................................................................2分 x x 由 f ¢( x )>0得x2；由 fx0得0x2 从而，函数 f x减区间为(0,2)，增区间为(2,)...............................................................................4 分 所以函数 f x极小值为 f 22ln2，无极大值.................................................................................6分 2 （2）由已知x 1,时， fx0恒成立，即xa 0恒成立， x 2  2 即a x 恒成立，则ax  .......................................................................................................8分 x  x min 令函数gxx 2 x1，由gx1 2 0知gx在 1,单调递增，.................................9分 x x2 答案第6页，共9页 {#{QQABIYaQggggQAIAAAhCUwFiCgAQkBCCAKoORBAAsAABAANABAA=}#}从而agx g11.......................................................................................................................10分 min 经检验知，当a1时，函数 f x不是常函数，所以a的取值范围是a1...................................12分 3 2 20．(1)ac 4 1 (2) 2 【详解】（1）若选①a2 b2 c2 2， 由余弦定理可得b2 a2c22accosB， ∴1accosB，...................................................................................................................................2分 1 2 2 又sinB ，∴cosB 1sin2B  ，......................................................................................4分 3 3 3 2 ∴ac ．........................................................................................................................................6分 4   若选②ABBC1，   则 AB BC cosBaccosB 1，..............................................................................................2分 1 2 2 又sinB ，∴cosB 1sin2B  ，......................................................................................4分 3 3 3 2 ∴ac ．.........................................................................................................................................6分 4 a b c （2）由正弦定理   2R（R为ABC外接圆半径）， sinA sinB sinC 可得ac  2Rsin A2RsinC  4R2sin AsinC ， 2 3 2 又∵sinAsinC ，ac .........................................................................................................8分 3 4 3 2 2 3 ∴ 4R2 ，解得R ．.......................................................................................................10分 4 3 4 3 1 1 ∴b2RsinB2   ．..............................................................................................................12分 4 3 2 1 4 33 21．（1） ；（2） . 2 10   【详解】（1） f(x)2cos2x12 3cosxsinxcos2x 3sin2x2sin 2x ，...........4分  6     由于直线x 是函数 f(x)2sin2x 的一条对称轴， 3  6 2  2   sin  1，  k (kZ)，.................................................................................5分  3 6 3 6 2 3 1 1 1 1  k (kZ)，又01， k  ，kZ，从而k 0， ................................6分 2 2 3 3 2   1 2  （2） f(x)2sinx ，由题意可得g(x)2sin x   ，  6 2 3  6 答案第7页，共9页 {#{QQABIYaQggggQAIAAAhCUwFiCgAQkBCCAKoORBAAsAABAANABAA=}#}1     6   3 则g(x)2cos x，∵g2 2cos  ，cos  ，..........................................7分 2  3  6 5  6 5     2   4 又0, ，   ，sin  ， ..................................................................8 分  2 6 6 3  6 5          sinsin   sin cos cos sin ................................................................10分  6 6  6 6  6 6 4 3 3 1 4 3 3      .................................................................................................................................12分 5 2 5 2 10 22．(1)y1 (2)见解析 (3) 2e,0   6   e3 【详解】（1）解：若a1，则 f xexx， fxex1， 由 f 01, f00， 曲线y f x在点(0, f 0)处的切线方程为y1；..................................................................................2分 （2）解：函数 f x的定义域为,， fxaex1， 当a0时， fx0，所以 f x在,上单调递减；....................................................................4分 当a>0时，当xln 1 时， fx0，当xln 1 时， f ¢( x )>0 a a 1 1 所以 f x在(,ln )上单调递减， f x在(ln ,)上单调递增；......................................................6分 a a 综上，当a0时， f x在,上单调递减； 1 1 当a>0时， f x在(,ln )上单调递减，在(ln ,)上单调递增；......................................................7分 a a （3）解：gxaexxx2x3aexx23， 函数gx有两个零点，即方程aex x230有两个不相等的实数根， x23 也即方程a 有两个不相等的实数根，................................................................................................8分 ex x23 即直线ya与函数y 的图像有两个交点， ex x23 2xx23 x1x3 令hx ，则hx  ， ex ex ex 当x3或x1时，hx0，当1x3时，hx0， 所以函数hx在,1和3,上递减，在1,3上递增， 答案第8页，共9页 {#{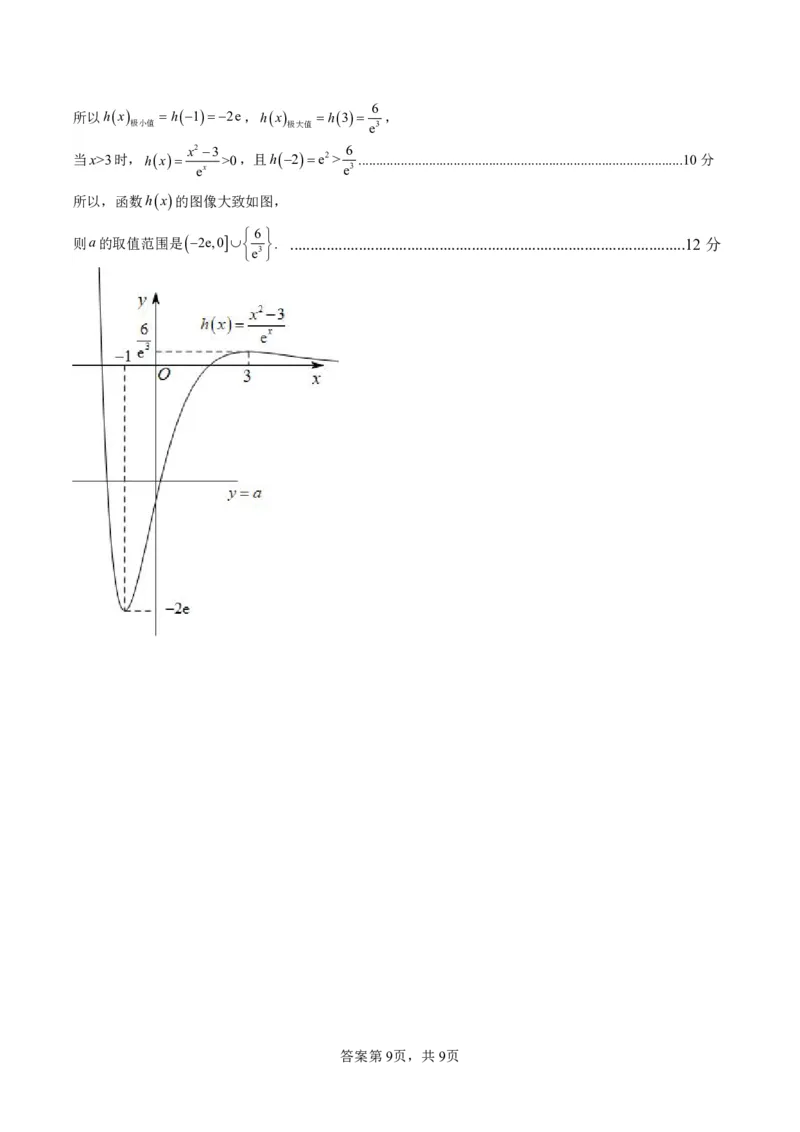QQABIYaQggggQAIAAAhCUwFiCgAQkBCCAKoORBAAsAABAANABAA=}#}所以hx h12e，hx h3 6 ， 极小值 极大值 e3 当x>3时，hx x23 >0，且h2e2> 6 ............................................................................................10分 ex e3 所以，函数hx的图像大致如图， 则a的取值范围是 2e,0   6  . ..................................................................................................12分 e3 答案第9页，共9页 {#{QQABIYaQggggQAIAAAhCUwFiCgAQkBCCAKoORBAAsAABAANABAA=}#}