文档内容
2024-2025 学年浙江省杭州市高二上学期 1 月期末考试数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合A={x|−30) O F C
a2 b2
1
H,若△FOH的内切圆的半径r= b,则双曲线C的离心率为( )
4
5 4 5 3
A. B. C. D.
3 3 4 5
第 页,共 页
1 1二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.在空间直角坐标系中,已知点A(1,1,0),B(1,0,2),C(2,−1,5),D(1,−2,4),则下列结论正确的是
( )
A. ⃗ B. , , 三点共线
AB=(0,−1,2) A B C
7 7
C. AD⊥BC D. ⃗AC在⃗BD上的投影向量为(0,− , )
2 2
10.已知圆 ,圆 ,则下列说法正确的是( )
C :x2+ y2−2x−4 y=0 C :x2+ y2+mx+ny=0
1 2
A. 圆C ,C 恒有公共点
1 2
B. 圆C ,C 至多有三条公切线
1 2
C. 若圆C 平分圆C 的周长,则m+2n=10
2 1
D. 若圆C 平分圆C 的周长,则n2−m的最小值为9
2 1
11.已知椭圆 x2 y2 的左、右焦点分别为 , ,上顶点为 ,离心率为√3, ,
C: + =1(a>b>0) F F B(0,1) M
a2 b2 1 2 2
N为C上关于原点对称的两点(与C的顶点不重合),则下列说法正确的是( )
x2 1 9
A. 椭圆C的方程为 + y2=1 B. + ≥5
4 |M F | |N F |
1 1
1
C. 直线BM与BN的斜率乘积为− D. △MN F 的面积随周长变大而变大
4 2
三、填空题:本题共3小题,每小题5分,共15分。
12.直线2√3x+2y+3=0的倾斜角为
13.在四棱锥P−ABCD中,底面ABCD是边长为a的正方形,PA⊥平面ABCD.若PA=a,则直线PB与
平面PCD所成的角的大小为
14.设P(x ,y ),Q(x ,y )是平面直角坐标系xOy上的两点,O为坐标原点,定义点P到点Q的一种折线
1 1 2 2
x2
距离d(P,Q)=|x −x |+|y −y |.已知P(0,2),Q是曲线 −y2=1(x>0)上一点,则d(P,Q)的最
1 2 1 2 2
小值为 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题12分)
第 页,共 页
2 1π
在△ABC中,内角A,B,C所对的边分别为a,b,c,已知asinB=bcos(A− ).
6
(1)求角A的大小;
2√3
(2)若c=2b,△ABC的面积为 ,求△ABC的周长.
3
16.(本小题12分)
已知定义在 上的函数 是偶函数.
R f(x)=2x+a⋅2−x
(1)求a的值;
(2)当x∈[−1,1]时,函数g(x)=f(2x)−λf(x)的最小值为−2,求λ的值.
17.(本小题12分)
π
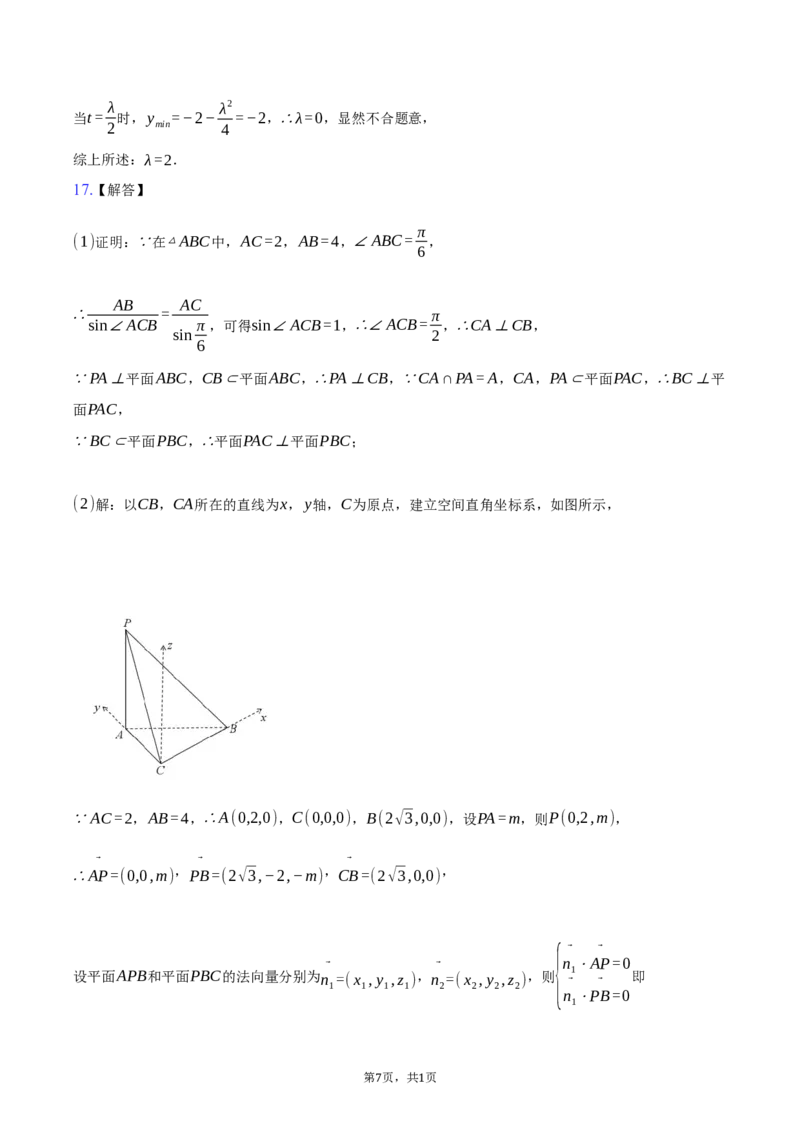
在三棱锥P−ABC中,PA⊥平面ABC,AC=2,AB=4,∠ABC= .
6
(1)求证:平面PAC⊥平面PBC;
√6
(2)若二面角A−PB−C的余弦值为 ,求PA的长度.
4
18.(本小题12分)
已知抛物线 的准线方程为 ,直线 交抛物线 于 , 两点.
E:y2=2px(p>0) x=−1 l:x=my+3 E A B
(1)求抛物线E的方程;
第 页,共 页
3 1(2)若|AB|=4√15,求m的值;
(3)若抛物线E上存在两点C,D关于直线l对称,求m的取值范围.
19.(本小题12分)
17世纪80年代,天文学家卡西尼在研究土星及其卫星的运行规律时发现:同一平面内到两个定点的距离之
积为常数的点的轨迹是卵形线,我们称之为卡西尼卵形线.在平面直角坐标系xOy中,O为坐标原点,已知
两定点F (−1,0),F (1,0),动点P(x,y)满足|PF |⋅|PF |=3,动点P的轨迹为曲线E,直线
1 2 1 2
y=kx+b与曲线E相交于A,B两点,线段AB的中点为M,直线OM的斜率为k .
0
(1)求曲线E的方程;
(2)求|OP|的取值范围;
3 1
(3)求证:− 0,因此cosA>0,
sinA π
所以tanA= =√3,所以A= ;
cosA 3
2√3
(2)由△ABC的面积为 ,
3
1 2√3 8
得 bcsin A= ,解得bc= ,
2 3 3
第 页,共 页
5 12 4
又c=2b,则b= √3,c= √3,
3 3
16 4 8
由余弦定理得a2=c2+b2−2bccosA= + − =4,
3 3 3
解得a=2,b+c=2√3,
所以△ABC的周长为2√3+2.
16.解:
是偶函数, ,
(1)∵f(x)=2x+a⋅2−x ∴f(x)=f(−x)
即 ,即 , ;
2x+a⋅2−x=2−x+a⋅2x (a−1)(2x−2−x )=0 ∴a=1
由 可知, ,
(2) (1) f(x)=2x+2−x
,
∴g(x)=22x+2−2x−λ(2x+2−x )=(2x+2−x ) 2−λ(2x+2−x )−2
5
令t=2x+2−x,由−1≤x≤1,可得t∈[2, ],
2
5
∴上述函数转化为y=t2−λt−2(t∈[2, ]),
2
5
当λ≤4时,y=t2−λt−2在[2, ]上单调递增,
2
当t=2时,y =2−2λ=−2,∴λ=2≤4,λ=2满足题意;
min
5
当λ≥5时,y=t2−λt−2在[2, ]上单调递减,
2
5 17−10λ 5
当t= 时,y = =−2,∴λ= <5不合题意;
2 min 4 2
λ λ 5
当4<λ<5时,y=t2−λt−2在[2, ]上单调递减,在( , ]上单调递增,
2 2 2
第 页,共 页
6 1λ λ2
当t= 时,y =−2− =−2,∴λ=0,显然不合题意,
2 min 4
综上所述:λ=2.
17.【解答】
π
(1)证明:∵在△ABC中,AC=2,AB=4,∠ABC= ,
6
AB AC
∴ = π
sin∠ACB π ,可得sin∠ACB=1,∴∠ACB= ,∴CA⊥CB,
sin 2
6
∵PA⊥平面ABC,CB⊂平面ABC,∴PA⊥CB,∵CA∩PA=A,CA,PA⊂平面PAC,∴BC⊥平
面PAC,
∵BC⊂平面PBC,∴平面PAC⊥平面PBC;
(2)解:以CB,CA所在的直线为x,y轴,C为原点,建立空间直角坐标系,如图所示,
∵AC=2,AB=4,∴A(0,2,0),C(0,0,0),B(2√3,0,0),设PA=m,则P(0,2,m),
⃗ ⃗ ⃗
∴AP=(0,0,m) ,PB=(2√3,−2,−m) ,CB=(2√3,0,0) ,
{⃗ ⃗
n ⋅AP=0
设平面APB和平面PBC的法向量分别为n ⃗ =(x ,y ,z ) ,n ⃗ =(x ,y ,z ) ,则 1 即
1 1 1 1 2 2 2 2 ⃗ ⃗
n ⋅PB=0
1
第 页,共 页
7 1{ mz =0
2√3x −2y
1
−mz =0
,令x
1
=1,可得n ⃗
1
=(1,√3,0) ,
1 1 1
{⃗ ⃗
n ⋅CB=0 { 2√3x =0
同理
⃗
2
⃗
即
2√3x −2y
2
−mz =0
,令y
2
=m,可得n ⃗
2
=(0,m,−2) ,
n ⋅PB=0 2 2 2
2
⃗ ⃗
|n ⋅n | √3m √6
显然二面角A−PB−C的平面角为锐角,记为θ,∴cosθ= 1 2 = = ,即m2=4,
⃗ ⃗ 2√m2+4 4
|n ||n |
1 2
∴m=2或m=−2(舍去),故PA=2.
p
18.解:(1)由题意x=− =−1,∴p=2,抛物线E的方程为y2=4x;
2
由题意:{ y2=4x ,
(2)
x=my+3
整理得y2−4my−12=0,△=16m2+48>0, y + y =4m,y y =−12,
1 2 1 2
,整理可得 ,
∴|AB|=√1+m2√16m2+48=4√15 m4+4m2−12=0
, ;
∴(m2+6)(m2−2)=0 ∴m=±√2
a2 b2
(3)设C( ,a),D( ,b), 若m=0,则l:x=3,易得此时不合题意;
4 4
b−a 4
k = = =−m 4
若m≠0,由于C,D关于直线l对称,故 CD b2−a2 b+a ,可得a+b=− ,
m
4
2
∴CD中点的纵坐标为− ,
m
将其代入x=my+3中,可得x=1,
第 页,共 页
8 1a2 b2
+
又 4 4 a2+b2 ,化简可得a2+b2=8,
= =1
2 8
{a2+b2=8
,且 ,
∴ 4 a2≠b2
a+b=−
m
4 8
化简可得b2+ b+ −4=0,要使得上述关于b的方程有实根,
m m2
当Δ=0时a=b不合题意,
16 8
则Δ= −4( −4)>0,故m2>1,∴m>1或m<−1.
m2 m2
19.解: 由题意 ,
(1) √(x−1) 2+ y2 ⋅√(x+1) 2+ y2=3
整理可得 ,
(x2+ y2+1) 2−4x2=9
曲线 的方程为 ;
∴ E x2+ y2+1=√4x2+9
,
(2)|OP|2=x2+ y2=√4x2+9−1
由曲线 的方程可知 ,
E y2=√4x2+9−x2−1≥0
,即 ,
∴√4x2+9≥x2+1 x4−2x2−8≤0
解得−2≤x2≤4,∴x∈[−2,2],
,
∴|OP|2=x2+ y2=√4x2+9−1∈[2,4]
∴|OP|的取值范围为[√2,2];
(3)设A(x ,y ),B(x ,y ),M(x ,y ),
1 1 1 1 0 0
第 页,共 页
9 1{x2+ y2+1=√4x2+9
由题意可知 1 1 1 ,
x2+ y2+1=√4x2+9
2 2 2
则 ,
x2+ y2−(x2+ y2 )=√4x2+9−√4x2+9
2 2 1 1 2 1
4(x2−x2
)
(x2−x2 )+(y2−y2 )= 2 1 ,
2 1 2 1 √4x2+9+√4x2+9
2 1
由题意可知x ≠±x ,
1 2
y2−y2
4
∴1+ 2 1= ,
x2−x2 √4x2+9+√4x2+9
2 1 2 1
y + y
2 1
y −y y 2 y + y
由题意k= 2 1 ,k = 0= = 2 1 ,
x −x 0 x x +x x +x
2 1 0 2 1 2 1
2
4
∴1+k⋅k = ,
0 √4x2+9+√4x2+9
2 1
由(2)可知x ,x ∈[−2,2],
1 2
则 , ,
3≤√4x2+9≤5 3≤√4x2+9≤5
1 2
2 4 2
∴ < < ,
5 √4x2+9+√4x2+9 3
2 1
2 2 3 1
∴ <1+k⋅k < ,∴−