文档内容
第1 页共4 页
参考答案
1.C
2. D
3. C
4.B
5.B
6.D
7.A
8.A
9. AD
10.BCD
11.BCD
12.
3.0
13.
a
c
b
14.
1
eln2
15.(1)
2,0
1
log
3
1
8
2
2
2
x
x
x
B
x
A
,
,
.......................... 4 分
2
1,
B
A
,3
1,
A
CR
,3
2,
)
(
B
A
CR
.............7 分
(2)因为集合
2
C
x
x
a
,C
A
,
当
2
a
时,C ,满足条件;当
2
a
时,C ,则
3
a
,即2
3
a
,
综上所述,
,3
a
......................................................... 13 分
16.(1)
0
)
(
x
f
的解集为
2,1
, 2,1
是方程
0
)
(
x
f
的根且
0
k
k
k
k
2
2
1
1
2
2
1
1
k
2
3
)
(
2
x
x
x
f
................................. 5 分
(2)当
0
k
时,
2
)
(
x
x
f
,
0
2
0
)
(
x
x
f
,
2
x
................ 6 分
当
0
k
时,
)1
)(
2
(
)
(
kx
x
x
f
,即
0
)1
)(
2
(
kx
x
,即
0
)
1
)(
2
(
k
x
x
k
当
0
k
时,
0
)
1
)(
2
(
k
x
x
,
k
x
x
1
2
或
.............................. 8 分
当
0
k
时,
0
)
1
)(
2
(
k
x
x
(ⅰ)当
2
1
k
时,无解........................................................10 分
(ⅱ)当
2
1
k
时,
2
1
x
k
.................................................. 12 分
(ⅲ)当
2
1
k
时,
k
x
1
2
.................................................. 14 分
综上所述:当
0
k
时,不等式的解集为
k
x
x
x
1
2或
当
0
k
时,不等式的解集为
2
x
x
当
2
1
0
k
时,不等式的解集为
k
x
x
1
2
当
2
1
k
时,不等式的解集为
当
2
1
k
时,不等式的解集为
2
1
x
k
x
........................... 15 分
{#{QQABZYCEogAgAJJAARhCQwl4CEIQkAEAAagGxEAEsAAAwBFABAA=}#}
第2 页共4 页
17.(1)提出假设
0
H :周平均锻炼时长与年龄无关联,
由2
2
列联表中的数据,可得
2
2
0.001
500
(80
240
120
60)
500
23.81
10.828
200
300 140
360
21
x
,
根据小概率值
0.001
的独立性检验,我们推断
0
H 不成立,
即认为周平均锻炼时长与年龄有关联;.......................................... 7 分
(2)抽取的10 人中,周平均锻炼时长少于 小时的有
60
10
2
300
(人),
不少于 小时的有
240
10
8
300
(人),.......................................... 9 分
则X 所有可能的取值为1,2,3,
所以
2
1
2
8
3
10
1
(
1)
15
C C
P X
C
,
1
2
2
8
3
10
7
(
2)
15
C C
P X
C
,
3
8
3
10
7
(
3)
15
C
P X
C
,
所以随机变量X 的分布列为:
X
1
2
3
P
1
15
7
15
7
15
所以数学期望
1
7
7
12
(
)
1
2
3
15
15
15
5
E X
.................................. 15 分
18.(1)因为PA 平面ABCD,而AD 平面ABCD,所以PA
AD
,
又AD
PB
,PB
PA
P
,
,
PB PA 平面PAB ,所以AD 平面PAB ,
而AB 平面PAB ,所以AD
AB
.
因为
2
2
2
BC
AB
AC
,所以BC
AB
,根据平面知识可知
/ /
AD
BC ,
又AD 平面PBC ,BC 平面PBC ,所以
/ /
AD
平面PBC .........................7 分
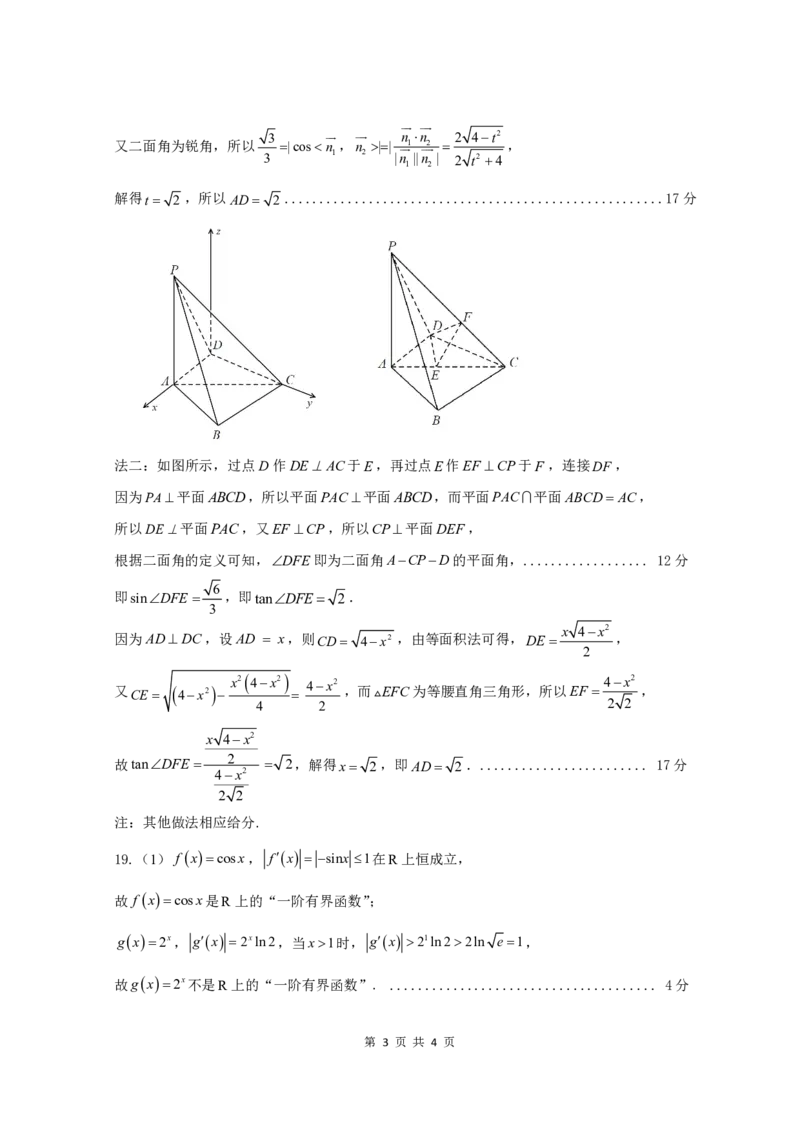
(2)法一:以DA ,DC 为x ,y 轴,过点D 作平面ABCD 垂直的线为z 轴,建立如图所示空间
直角坐标系
:
D
xyz
令AD
t
,则
(
A t ,0,0) ,
(
P t ,0,2) ,
(0
D
,0,0) ,
2
4
DC
t
,
(0
C
,
2
4
t
,0) ,.............................................9 分
设平面ACP 的法向量
1
1
(
n
x
,
1y ,
1)
z
,所以
2
1
1
1
1
4
0
2
0
n
AC
tx
t y
z
,
设
2
1
4
x
t
,则
1y
t
,
1
0
z
,所以
2
1
( 4
n
t
,t ,0) ,.......................11 分
设平面CPD 的法向量为
2
2
(
n
x
,
2y ,
2)
z
,所以
2
2
2
2
2
2
2
0
4
0
n
DP
tx
z
n
DC
t y
,
设
2z
t
,则
2
2
x ,
2
0
y
,所以
2
( 2
n
,0,)t ,..............................13 分
因为二面角A
CP
D
的正弦值为
6
3
,则余弦值为
3
3
,
{#{QQABZYCEogAgAJJAARhCQwl4CEIQkAEAAagGxEAEsAAAwBFABAA=}#}
第3 页共4 页
又二面角为锐角,所以
1
| cos
3
3
n
,
2
1
2
2
2
1
2
2 4
| |
|
||
|
2
4
n
n
t
n
n
n
t
,
解得
2
t
,所以
2
AD
......................................................17 分
法二:如图所示,过点D 作DE
AC
于E ,再过点E 作EF
CP
于F ,连接DF ,
因为PA 平面ABCD,所以平面PAC 平面ABCD,而平面PAC 平面ABCD
AC
,
所以DE 平面PAC ,又EF
CP
,所以
CP
平面DEF ,
根据二面角的定义可知,
DFE
即为二面角A
CP
D
的平面角,.................. 12 分
即
6
sin
3
DFE
,即tan
2
DFE
.
因为AD
DC
,设AD
x
,则
2
4
CD
x
,由等面积法可得,
2
4
2
x
x
DE
,
又
2
2
2
2
4
4
4
4
2
x
x
x
CE
x
,而EFC
为等腰直角三角形,所以
2
4
2 2
x
EF
,
故
2
2
4
2
tan
2
4
2 2
x
x
DFE
x
,解得
2
x
,即
2
AD
......................... 17 分
注:其他做法相应给分.
19.(1)
cos
f x
x
,
sin
1
f
x
x
在R 上恒成立,
故
cos
f x
x
是R 上的“一阶有界函数”;
2x
g x
,
2 ln 2
x
g
x
,当
1
x 时,
12 ln 2
2ln
1
g
x
e
,
故
2x
g x
不是R 上的“一阶有界函数”.
...................................... 4 分
{#{QQABZYCEogAgAJJAARhCQwl4CEIQkAEAAagGxEAEsAAAwBFABAA=}#}
第4 页共4 页
(2)正确. 若函数
f x 为R 上的“一阶有界函数”,则
1
f
x
,
又
f x 在R 上单调递减,即
0
x
f
,所以
1
0
f
x
,
令
F x
f x
x
,
1
0
F
x
f
x
,所以
( )
F x 在R 上单调递增,
设
1
1
( ,
)
A x y
,
2
2
(
,
)
B x
y
,其中
1
2
x
x
1
2
1
1
2
2
1
2
1
2
1
2
1
2
1
1
0
f x
f x
f x
x
f x
x
F x
F x
k
x
x
x
x
x
x
)
(
,故
1
k ;
又
f x 在R 上单调递减,所以
1
2
f x
f x
,
1
2
1
2
0
f
x
f
x
k
x
x
,故1
0
k
;... 10 分
(3)函数
3
2
e
e
1
x
h x
ax
x
a
x
,
2
e
3
2e
1
x
h x
ax
x
a
若( )
h x 为区间[0,1] 上的“一阶有界函数”,则
1
h
x
,
1
1
h x
对
0,1
x
恒成立
则
0
1
h
,2
1
a
,1
3
a
;
1
1
h
,2
e 1
1
a
,e
2
e
2
2
a
,
则
e
1
2
a
≤
≤
.................................................................. 12 分
令
2
e
3
2e
1
x
T x
h x
ax
x
a
,
e
6
2e
x
T
x
ax
,其中
e
1
2
a
≤
≤
,
因为
ex
y
,
6
y
ax
在区间[0,1] 上单调递增,所以
e
6
2e
x
T
x
ax
在区间[0,1] 上单调递增,
0
1 2e
0
T
,
1
6
e
0
T
a
,所以存在
0
0,1
x
,使
0
0
T
x
,即
0
0
e
6
2e
0
x
ax
,
当
0
0
x
x
时,
0
T
x
,
( )
T x 单调递减;当
0
1
x
x
,
0
T
x
,
( )
T x 单调递增.
所以,
h x
在区间
0
0, x
单调递减,在区间
0,1
x
单调递增,
所以
0
2
2
0
0
0
0
0
min
e
3
2e
1
3
6
2e
2e
1
x
h x
h x
ax
x
a
ax
a
x
a
,.......... 14 分
所以
0
1
h x
在区间
0
0,1
x
时有解,
因为对称轴为
6
2e
e
1
1
6
3
a
x
a
a
,
0
h x
在区间
0
0,1
x
上单调递减,
所以
0
2
1
1,
2
2
h
e
a
a
e
,........................................... 16 分
综上:
e
1, 2
a
.............................................................. 17 分
{#{QQABZYCEogAgAJJAARhCQwl4CEIQkAEAAagGxEAEsAAAwBFABAA=}#}