文档内容
深圳市 2020 年中考数学试卷
一、选择题(每小题3分,共12小题,满分36分)
1. 2020的相反数是( )
A.2020 B. C.-2020 D.
2. 下列图形中既是轴对称图形,也是中心对称图形的是( )
A. B. C. D.
3. 2020年6月30日,深圳市总工会启动“百万职工消费扶贫采购
节”活动,预计撬动扶贫消费额约
150 000 000元。将150 000 000用科学记数法表示为( )
A. B. C. D.
4. 下列哪个图形,主视图、左视图和俯视图相同的是( )
A.圆锥 B.圆柱 C.三棱柱 D.正方体
5. 某同学在今年的中考体育测试中选考跳绳。考前一周,他记录了自己五次跳
绳的成绩(次数/分钟):247,253,247,255,263.这五次成绩的平均数和中位数分别是
()( )
A.253,253 B.255,253 C.253,247 D.255,247
6. 下列运算正确的是(
A. B.
C. D.
300
7. 一把直尺与 30°的直角三角板如图所示,
∠1=40°,则∠2=( )
2
1A.50° B.60° C.70° D.80°
8. 如图,已知AB=AC,BC=6,山尺规作图痕迹可求出BD=( )
A.2 B.3 C.4 D.5
9. 以下说法正确的是( )
A.平行四边形的对边相等 B.圆周角等于圆心角的一半
C.分式方程 的解为x=2 D.三角形的一个外角等于两个内角的和
10. 如图,为了测量一条河流的宽度,一测量员
在河岸边相距200米的P、Q两点分别测定对岸一棵
树T的位置,T在P的正北方向,且T在Q的北偏西
70°方向,则河宽(PT的长)可以表示为() (
)
A.200tan70°米 B. 米
C.200sin70°米 D. 米
y
(-1,n)
11. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,
下列说法错误的是( )
(-3,0) x
O
A. B.4ac-b2<0
C.3a+c>0 D.ax2+bx+c=n+1无实数根
12. 如图,矩形纸片ABCD中,AB=6,BC=12.将纸片折叠,使点B落在边AD的
延长线上的点G处,折痕为EF,点E、F分别在边AD和边BC上。连接BG,交CD
于点K,FG交CD于点H。给出以下结论:
① EF⊥BG;②GE=GF;③△GDK和△GKH的面积相等;
④当点F与点C重合时,∠DEF=75°
其中正确的结论共有( )
A.1个 B.2个 C.3个 D.4
个二、填空题(每小题3分,共4小题,满分12分)
13. 分解因式:m3-m= .
14. 口袋内装有编号分别为1,2,3,4,5,6,7的七个球(除编号外都相同),从中随机
摸出一个球,则摸出编号为偶数的球的概率是 .
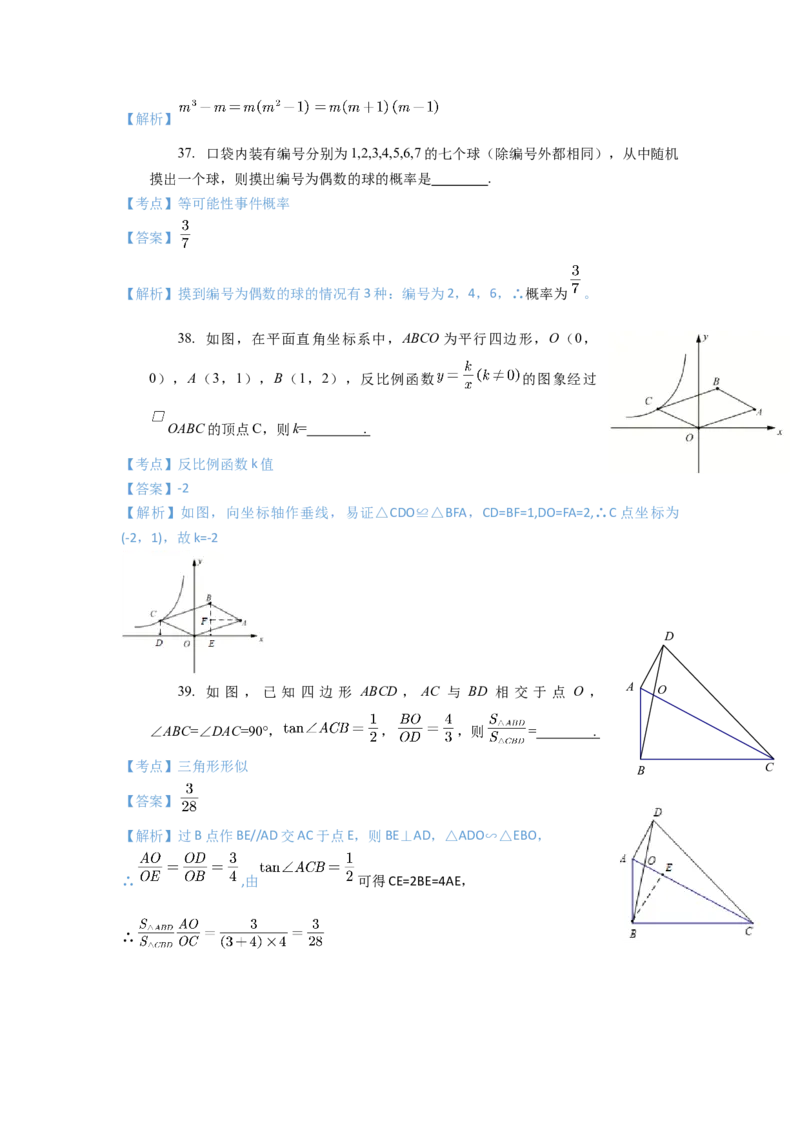
15. 如图,在平面直角坐标系中,ABCO为平行四边形,O(0,
0),A(3,1),B(1,2),反比例函数 的图象经过
OABC的顶点C,则k= .
16. 如 图 , 已 知 四 边 形 ABCD , AC 与 BD 相 交 于 点 O ,
∠ABC=∠DAC=90° , , ,则
D
= .
A O
B C
三、解答题(第 17题5分,第18题6分,第19题7分,第
20题8分,第21题8分,第22题9分,第23题9分,满分52分)
17. 计算:
18. 先化简,再求值: ,其中a=2.
19. 以人工智能、大数据、物联网为基础的技术创新促进了新业态蓬勃发展,新
业态发展对人才的需求更加旺盛。某大型科技公司上半年新招聘软件、硬件、总线、
测试四类专业的毕业生,现随机调査了m名新聘毕业生的专业情况,并将调查结果绘
测试
n %
软件
总线
30%
硬件
40%人数/名
25
20
制成如下两幅不完整的统计图:
15
10
5
0
软件 硬件 总线 测试 专业类别
根据以上信息,解答下列问题:
(1)m= ,n= .
(2)请补全条形统计图;
(3)在扇形统计图中,“软件”所对应圆心角的度数是 .
(4)若该公司新聘600名毕业生,请你估计“总线”专业的毕业生有 名
20. 如图,AB为⊙O的直径,点C在⊙O上,AD与过点C的切线互相垂直,垂
足为D.连接BC并延长,交AD的延长线于点E
E
(1)求证:AE=AB
(2)若AB=10,BC=6,求CD的长
D
C
A B
O
21. 端午节前夕,某商铺用620元购进50个肉粽和30个蜜枣粽,肉粽的进货单
价比蜜枣粽的进货单价多6元
(1)肉粽和蜜枣粽的进货单价分别是多少元?
(2)由于粽子畅销,商铺决定再购进这两种粽子共300个,其中肉粽数量不多于蜜枣粽数
量的2倍,且每种粽子的进货单价保持不变,若肉粽的销售单价为14元,蜜枣粽的销售单
价为6元,试问第二批购进肉粽多少个时,全部售完后,第二批粽子获得利润最大?第二批粽子的最大利润是多少元?
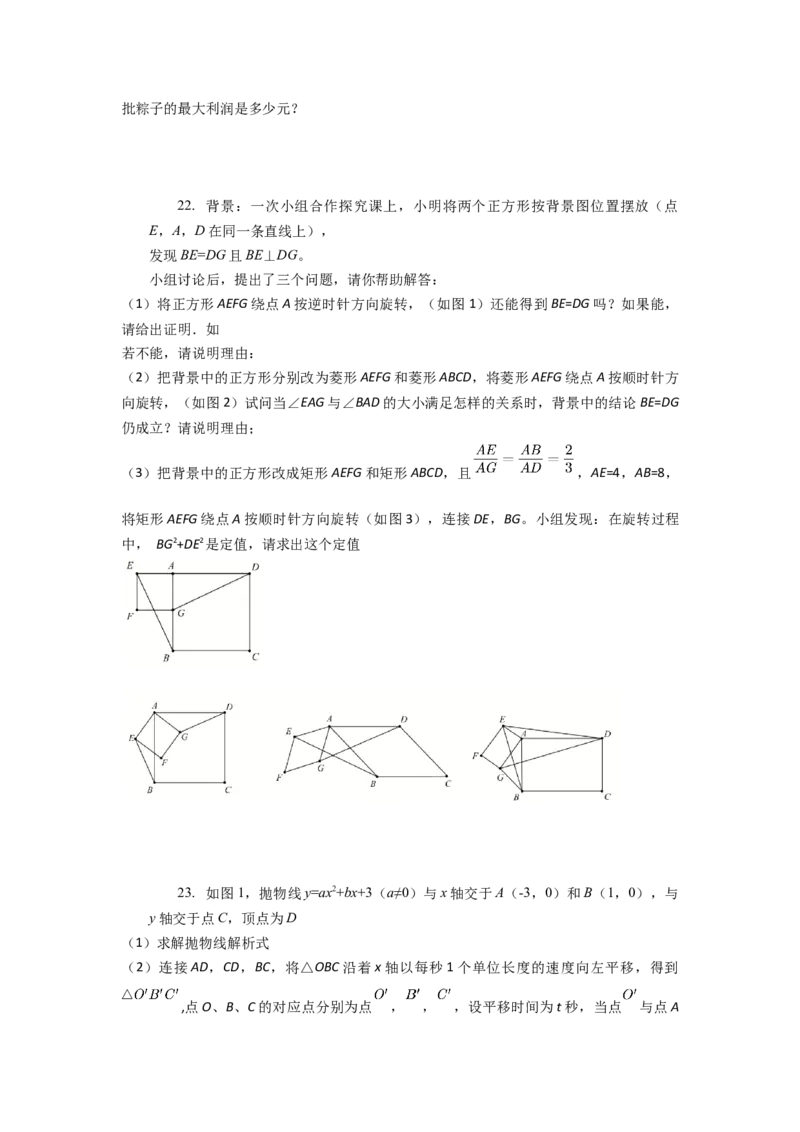
22. 背景:一次小组合作探究课上,小明将两个正方形按背景图位置摆放(点
E,A,D在同一条直线上),
发现BE=DG且BE⊥DG。
小组讨论后,提出了三个问题,请你帮助解答:
(1)将正方形AEFG绕点A按逆时针方向旋转,(如图1)还能得到BE=DG吗?如果能,
请给出证明.如
若不能,请说明理由:
(2)把背景中的正方形分别改为菱形AEFG和菱形ABCD,将菱形AEFG绕点A按顺时针方
向旋转,(如图2)试问当∠EAG与∠BAD的大小满足怎样的关系时,背景中的结论BE=DG
仍成立?请说明理由;
(3)把背景中的正方形改成矩形AEFG和矩形ABCD,且 ,AE=4,AB=8,
将矩形AEFG绕点A按顺时针方向旋转(如图3),连接DE,BG。小组发现:在旋转过程
中, BG2+DE2是定值,请求出这个定值
图1
23. 如图1,抛物线y=ax2+bx+3(a≠0)与x轴交于A(-3,0)和B(1,0),与
y轴交于点C,顶点为D
(1)求解抛物线解析式
(2)连接AD,CD,BC,将△OBC沿着x轴以每秒1个单位长度的速度向左平移,得到
,点O、B、C的对应点分别为点 , , ,设平移时间为t秒,当点 与点A重合时停止移动。记△ 与四边形AOCD的重叠部分的面积为S,请直接写出S与时
间t的函数解析式;
(3)如图2,过抛物线上任意一点M(m,n)向直线l: 作垂线,垂足为E,试问在
该抛物线的对称轴上是否存在一点F,使得ME-MF= ?若存在,请求F点的坐标;若不存
在,请说明理由。
y
D
C
x
A O B
图1
y
E
D 9
y=
2
C
M
x
A O B
图2深圳市 2020 年中考数学试卷
一、选择题(每小题3分,共12小题,满分36分)
24. 2020的相反数是( )
A.2020 B. C.-2020 D.
【考点】相反数
【答案】C
【解析】由相反数的定义可得选C。
25. 下列图形中既是轴对称图形,也是中心对称图形的是( )
A. B. C. D.
【考点】轴对称和中心对称
【答案】B
【解析】A图既不是轴对称也不是中心对称;C图为轴对称,但不是中心对称;D图为中心
对称,但不是轴对称,故选B。
26. 2020年6月30日,深圳市总工会启动“百万职工消费扶贫采购
节”活动,预计撬动扶贫消费额约
150 000 000元。将150 000 000用科学记数法表示为( )
A. B. C. D.
【考点】科学计数法
【答案】D
【解析】用科学计数法表示小数点需向左移动8位,故选D。
27. 下列哪个图形,主视图、左视图和俯视图相同的是( )A.圆锥 B.圆柱 C.三棱柱 D.正方体
【考点】三视图
【答案】D
【解析】分析以上立方体的三视图,可知三视图都相同的为D项。
28. 某同学在今年的中考体育测试中选考跳绳。考前一周,他记录了自己五次跳
绳的成绩(次数/分钟):247,253,247,255,263.这五次成绩的平均数和中位数分别是
()( )
A.253,253 B.255,253 C.253,247 D.255,247
【考点】数据的描述
【答案】A
【解析】求平均数可用基准数法,设基准数为250,则新数列为-4,3,-3,5,13,新数列
的平均数为3,则原数列的平均数为253;对数据从小到大进行排列,可知中位数为253,
故选A。
29. 下列运算正确的是(
A. B.
C. D.
【考点】整式的运算 300
【答案】B
【解析】A项结果应为3a,C项结果应为 ,D项结果应为 。
30. 一把直尺与 30°的直角三角板如图所示, 2
∠1=40°,则∠2=( ) 1
A.50° B.60° C.70°
D.80°
【考点】平行线的性质
【答案】D
A
【解析】令直角三角形中与30°互余的角为∠3,则 ,由两直线平行,同
B D C旁内角互补得: ,故选D。
31. 如图,已知AB=AC,BC=6,山尺规作图痕迹可求出BD=( )
A.2 B.3 C.4 D.5
【考点】等腰三角形的三线合一
【答案】B
【解析】由作图痕迹可知AD为 的角平分线,而AB=AC,由等腰三角形的三线合一
知D为BC重点, BD=3,故选B。
32. 以下说法正确的是( )
A.平行四边形的对边相等 B.圆周角等于圆心角的一半
C.分式方程 的解为x=2 D.三角形的一个外角等于两个内角的和
【考点】命题的真假
【答案】A
【解析】B没有强调同弧,同弧所对的圆周角等于圆心角的一半;C项x=2为增根,原分式
方程无解;D项没有指明两个内角为不想邻的内角,故错误。正确的命题为A。
33. 如图,为了测量一条河流的宽度,一测量员
在河岸边相距200米的P、Q两点分别测定对岸一棵
树T的位置,T在P的正北方向,且T在Q的北偏西
70°方向,则河宽(PT的长)可以表示为() (
)
A.200tan70°米 B. 米
C.200sin70°米 D. 米
【考点】直角三角形的边角关系
【答案】B
【解析】由题意知 ,则 ,变形可得选 y
(-1,n)
B。
34. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,
下列说法错误的是( )
(-3,0) x
OA. B.4ac-b2<0
C.3a+c>0 D.ax2+bx+c=n+1无实数根
【考点】二次函数综合
【答案】B
【解析】由图可知二次函数对称轴为x=-1,则根据对称性可得函数与x轴的另一交点坐标
为(1,0),代入
解析式y=ax2+bx+c可得b=2a,c=-3a,其中a<0。 b<0,c>0,3a+c=0,abc>0;二次函数与
x轴有两个交点, ,故B项错误;D项可理解为二次函数与直线y=n+1
无交点,显然成立。综上,此题选B。
35. 如图,矩形纸片ABCD中,AB=6,BC=12.将纸片折叠,使点B落在边AD的
延长线上的点G处,折痕为EF,点E、F分别在边AD和边BC上。连接BG,交CD
于点K,FG交CD于点H。给出以下结论:
① EF⊥BG;②GE=GF;③△GDK和△GKH的面积相等;
④当点F与点C重合时,∠DEF=75°
其中正确的结论共有( )
A.1个 B.2个 C.3个 D.4
个
【考点】几何综合
【答案】C
【解析】由折叠易证四边形EBFG为菱形,故EF⊥BG,GE=GF,∴①②正确;
KG 平分 , , ,∴ , ,故③错
误 ; 当 点 F 与 点 C 重 合 时 , BE=BF=BC=12=2AB , ∴ ,
,故④正确。综合,正确的为①②④,选C。
二、填空题(每小题3分,共4小题,满分12分)
36. 分解因式:m3-m= .
【考点】因式分解
【答案】【解析】
37. 口袋内装有编号分别为1,2,3,4,5,6,7的七个球(除编号外都相同),从中随机
摸出一个球,则摸出编号为偶数的球的概率是 .
【考点】等可能性事件概率
【答案】
【解析】摸到编号为偶数的球的情况有3种:编号为2,4,6,∴概率为 。
38. 如图,在平面直角坐标系中,ABCO为平行四边形,O(0,
0),A(3,1),B(1,2),反比例函数 的图象经过
OABC的顶点C,则k= .
【考点】反比例函数k值
【答案】-2
【解析】如图,向坐标轴作垂线,易证△CDO≌△BFA,CD=BF=1,DO=FA=2,∴C点坐标为
(-2,1),故k=-2
D
39. 如 图 , 已 知 四 边 形 ABCD , AC 与 BD 相 交 于 点 O , A O
∠ABC=∠DAC=90°, , ,则 = .
【考点】三角形形似 B C
【答案】
【解析】过B点作BE//AD交AC于点E,则BE⊥AD,△ADO∽△EBO,
∴ ,由 可得CE=2BE=4AE,
∴三、解答题(第17题5分,第18题6分,第19题7分,第20题8分,第21题8分,第
22题9分,第23题9分,满分52分)
40. 计算:
【考点】实数的计算
【答案】2
【解析】
解:
41. 先化简,再求值: ,其中a=2.
【考点】代数式的化简求值
【答案】
【解析】
解:
当a=2时,
42. 以人工智能、大数据、物联网为基础的技术创新促进了新业态蓬勃发展,新
业态发展对人才的需求更加旺盛。某大型科技公司上半年新招聘软件、硬件、总线、
测试四类专业的毕业生,现随机调査了m名新聘毕业生的专业情况,并将调查结果绘
测试
n %
软件
总线
30%
硬件
40%人数/名
25
20
制成如下两幅不完整的统计图:
15
10
5
0
软件 硬件 总线 测试 专业类别
根据以上信息,解答下列问题:
(1)m= ,n= .
(2)请补全条形统计图;
(3)在扇形统计图中,“软件”所对应圆心角的度数是 .
(4)若该公司新聘600名毕业生,请你估计“总线”专业的毕业生有 名
【考点】数据统计
【答案】(1)50,10(2)见解析(3)700(4)180
【解析】由统计图可知 , ,n=10。硬件专业的毕业生为
人数/名
25
20
人,则统计图为
15
10
5
0
软件 硬件 总线 测试 专业类别
软件专业的毕业生对应的占比为 ,所对的圆心角的度数为
。若该公司新聘 600 名毕业生 ,“总线” 专业 的毕业生 为
名。 E
43. 如图,AB为⊙O的直径,点C在⊙O上,AD与过点C的切 D
线互相垂直,垂足为D.连接BC并延长,交AD的延长线于点E
C
(1)求证:AE=AB
A B
O(2)若AB=10,BC=6,求CD的长
【考点】圆的证明与计算
【解析】
解:(1)证:连接OC
∵CD与 相切于C点
∴OC⊥CD
又∵CD⊥AE
∴OC//AE
∴
∵OC=OB
E
∴
D
∴
C
∴AE=AB
(2)连接AC
A B
∵AB为 的直径 O
∴
∴
∵AB=AE,AC⊥BE
∴EC=BC=6
∵ ,
∴△EDC∽△ECA
∴
∴
44. 端午节前夕,某商铺用620元购进50个肉粽和30个蜜枣粽,肉粽的进货单
价比蜜枣粽的进货单价多6元
(1)肉粽和蜜枣粽的进货单价分别是多少元?
(2)由于粽子畅销,商铺决定再购进这两种粽子共300个,其中肉粽数量不多于蜜枣粽数
量的2倍,且每种粽子的进货单价保持不变,若肉粽的销售单价为14元,蜜枣粽的销售单价为6元,试问第二批购进肉粽多少个时,全部售完后,第二批粽子获得利润最大?第二
批粽子的最大利润是多少元?
【考点】方程(组)与不等式
【解析】
解:(1)设肉粽和蜜枣粽的进货单价分别为x,y元,则根据题意可得:
解此方程组得:
答:肉粽得进货单价为10元,蜜枣粽得进货单价为4元
(2)设第二批购进肉粽t个,第二批粽子得利润为W,则
∵k=2>0
∴W随t的增大而增大。
由题意 ,解得
∴当t=200时,第二批粽子由最大利润,最大利润
答:第二批购进肉粽200个时,全部售完后,第二批粽子获得利润最大,最大利润为1000
元。
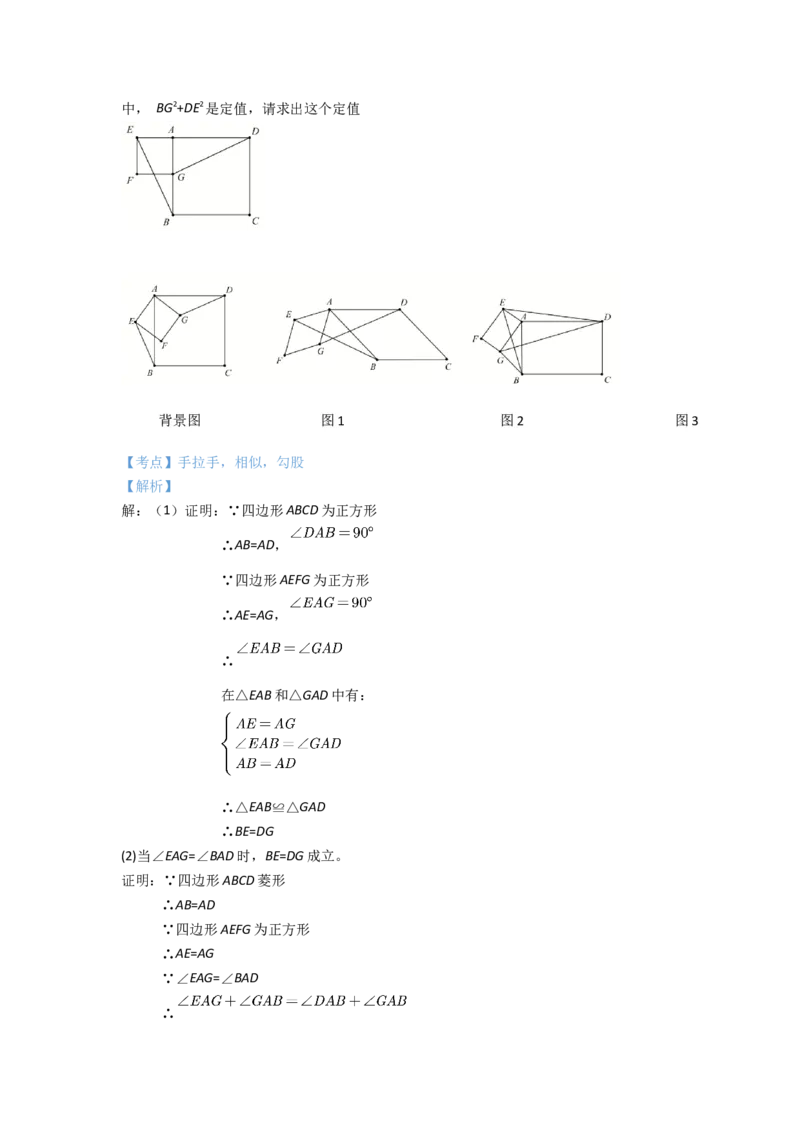
45. 背景:一次小组合作探究课上,小明将两个正方形按背景图位置摆放(点
E,A,D在同一条直线上),
发现BE=DG且BE⊥DG。
小组讨论后,提出了三个问题,请你帮助解答:
(1)将正方形AEFG绕点A按逆时针方向旋转,(如图1)还能得到BE=DG吗?如果能,
请给出证明.如
若不能,请说明理由:
(2)把背景中的正方形分别改为菱形AEFG和菱形ABCD,将菱形AEFG绕点A按顺时针方
向旋转,(如图2)试问当∠EAG与∠BAD的大小满足怎样的关系时,背景中的结论BE=DG
仍成立?请说明理由;
(3)把背景中的正方形改成矩形AEFG和矩形ABCD,且 ,AE=4,AB=8,
将矩形AEFG绕点A按顺时针方向旋转(如图3),连接DE,BG。小组发现:在旋转过程中, BG2+DE2是定值,请求出这个定值
背景图 图1 图2 图3
【考点】手拉手,相似,勾股
【解析】
解:(1)证明:∵四边形ABCD为正方形
∴AB=AD,
∵四边形AEFG为正方形
∴AE=AG,
∴
在△EAB和△GAD中有:
∴△EAB≌△GAD
∴BE=DG
(2)当∠EAG=∠BAD时,BE=DG成立。
证明:∵四边形ABCD菱形
∴AB=AD
∵四边形AEFG为正方形
∴AE=AG
∵∠EAG=∠BAD
∴∴
在△EAB和△GAD中有:
∴△EAB≌△GAD
∴BE=DG
(3)连接EB,BD,设BE和GD相交于点H
∵四边形AEFG和ABCD为矩形
∴
∴
∵
∴△EAB∽△GAD
∴
∴
∴ ,
∴
,
∴
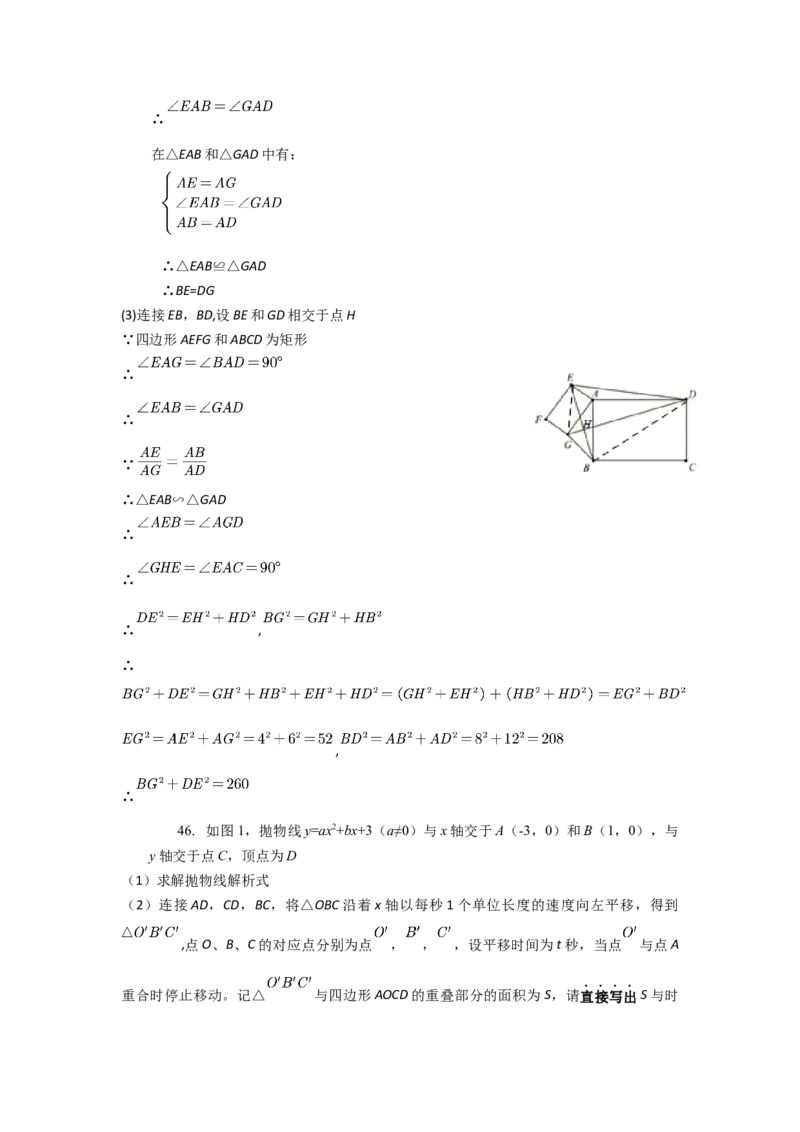
46. 如图1,抛物线y=ax2+bx+3(a≠0)与x轴交于A(-3,0)和B(1,0),与
y轴交于点C,顶点为D
(1)求解抛物线解析式
(2)连接AD,CD,BC,将△OBC沿着x轴以每秒1个单位长度的速度向左平移,得到
,点O、B、C的对应点分别为点 , , ,设平移时间为t秒,当点 与点A
重合时停止移动。记△ 与四边形AOCD的重叠部分的面积为S,请直接写出S与时间t的函数解析式;
(3)如图2,过抛物线上任意一点M(m,n)向直线l: 作垂线,垂足为E,试问在
该抛物线的对称轴上是否存在一点F,使得ME-MF= ?若存在,请求F点的坐标;若不存
在,请说明理由。
y
D
C
x
A O B
图1
y
E
D 9
y=
2
C
M
x
A O B
图2
【考点】二次函数,变量之间的关系,存在性问题
【解析】
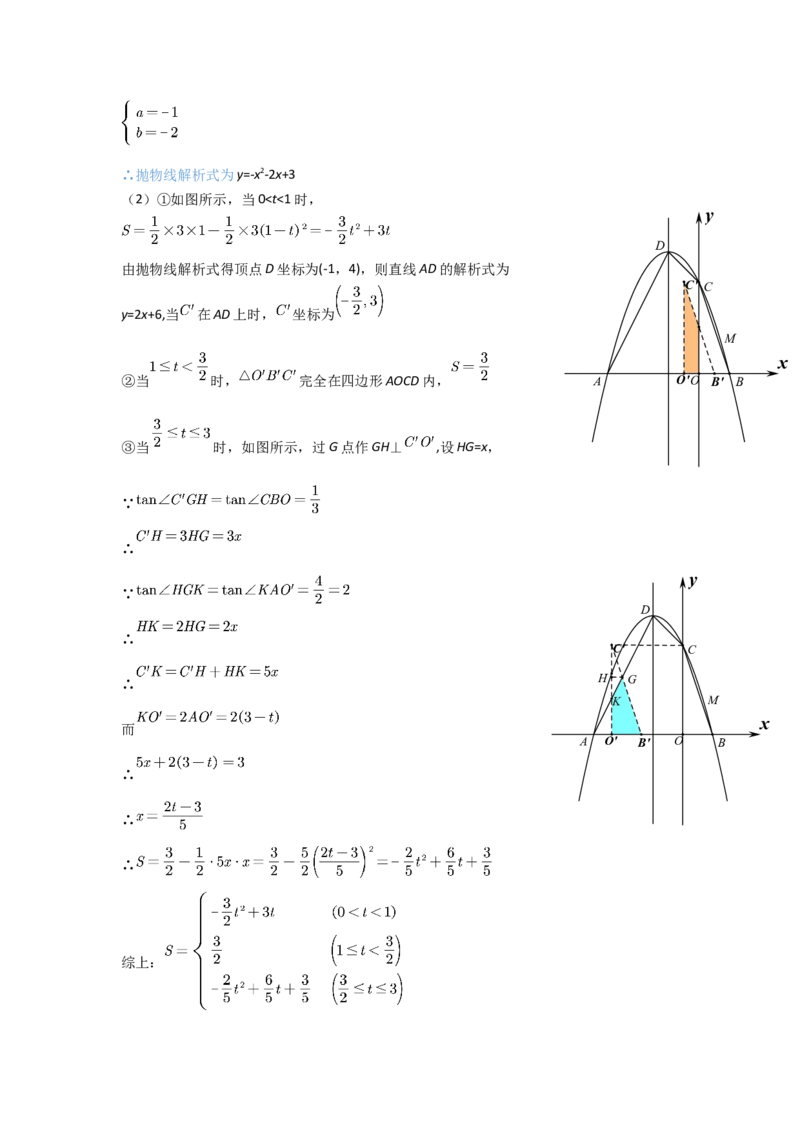
解:(1)将A(-3,0)和B(1,0)代入抛物线解析式y=ax2+bx+3中,可得:∴抛物线解析式为y=-x2-2x+3
(2)①如图所示,当0