文档内容
2020年重庆市中考数学试卷(A卷)
一、选择题:(本大题12个小题,每小题4分,共48分)在每个小题的下面,都给出了
代号为A、B、C、D的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答
案所对应的方框涂黑.
1.(4分)下列各数中,最小的数是( )
A.﹣3 B.0 C.1 D.2
2.(4分)下列图形是轴对称图形的是( )
A. B.
C. D.
3.(4分)在今年举行的第127届“广交会”上,有近26000家厂家进行“云端销售”.
其中数据26000用科学记数法表示为( )
A.26×103 B.2.6×103 C.2.6×104 D.0.26×105
4.(4分)把黑色三角形按如图所示的规律拼图案,其中第 个图案中有1个黑色三角形,
第 个图案中有3个黑色三角形,第 个图案中有6个黑①色三角形,…,按此规律排列
下②去,则第 个图案中黑色三角形的③个数为( )
⑤
A.10 B.15 C.18 D.21
5.(4分)如图,AB是 O的切线,A为切点,连接OA,OB,若∠B=20°,则∠AOB的
度数为( ) ⊙A.40° B.50° C.60° D.70°
6.(4分)下列计算中,正确的是( )
A. + = B.2+ =2 C. × = D.2 ﹣2=
7.(4分)解一元一次方程 (x+1)=1﹣ x时,去分母正确的是( )
A.3(x+1)=1﹣2x B.2(x+1)=1﹣3x
C.2(x+1)=6﹣3x D.3(x+1)=6﹣2x
8.(4分)如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(1,2),B(1,
1),C(3,1),以原点为位似中心,在原点的同侧画△DEF,使△DEF与△ABC成
位似图形,且相似比为2:1,则线段DF的长度为( )
A. B.2 C.4 D.2
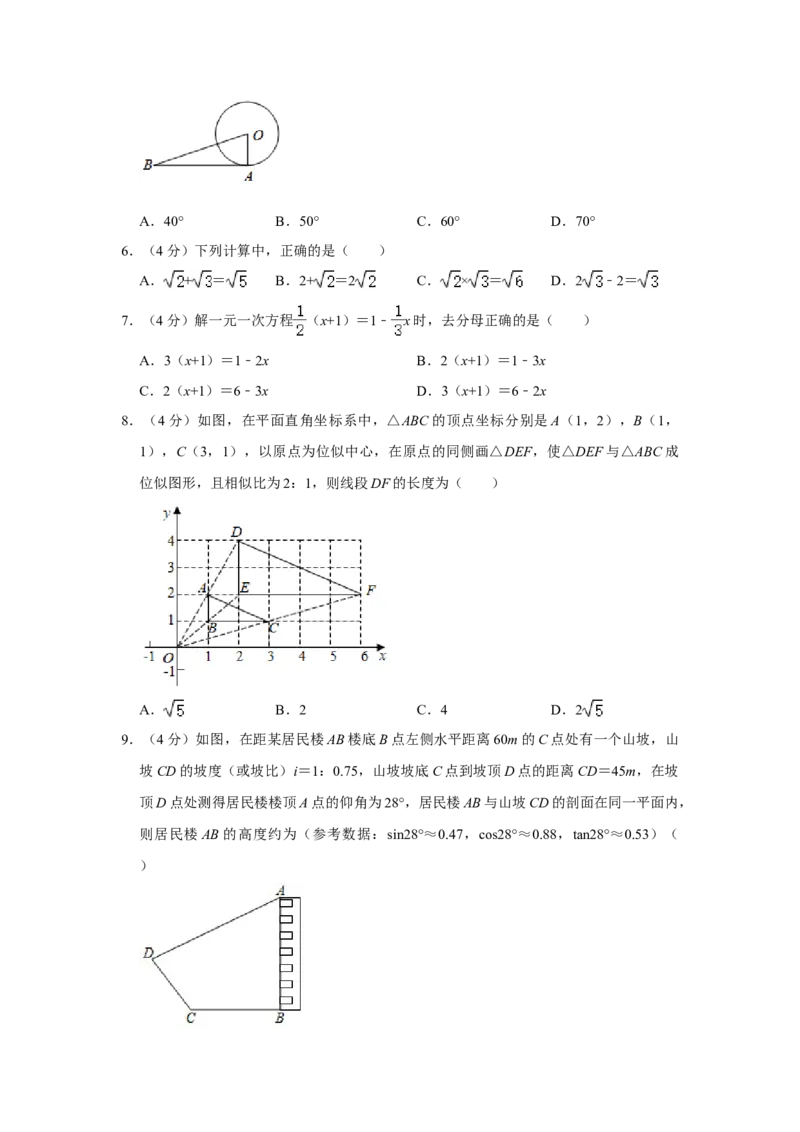
9.(4分)如图,在距某居民楼AB楼底B点左侧水平距离60m的C点处有一个山坡,山
坡CD的坡度(或坡比)i=1:0.75,山坡坡底C点到坡顶D点的距离CD=45m,在坡
顶D点处测得居民楼楼顶A点的仰角为28°,居民楼AB与山坡CD的剖面在同一平面内,
则居民楼AB的高度约为(参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)(
)A.76.9m B.82.1m C.94.8m D.112.6m
10.(4分)若关于x的一元一次不等式组 的解集为x≤a;且关于y的分
式方程 + =1有正整数解,则所有满足条件的整数a的值之积是( )
A.7 B.﹣14 C.28 D.﹣56
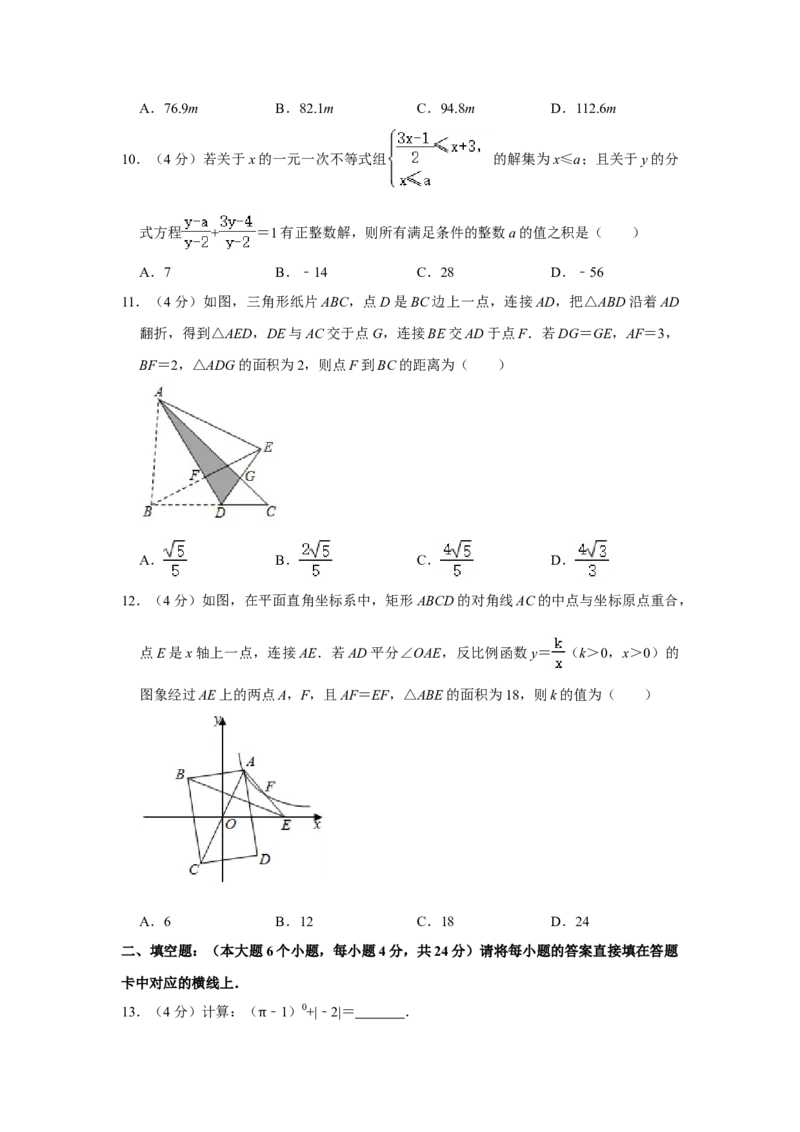
11.(4分)如图,三角形纸片ABC,点D是BC边上一点,连接AD,把△ABD沿着AD
翻折,得到△AED,DE与AC交于点G,连接BE交AD于点F.若DG=GE,AF=3,
BF=2,△ADG的面积为2,则点F到BC的距离为( )
A. B. C. D.
12.(4分)如图,在平面直角坐标系中,矩形ABCD的对角线AC的中点与坐标原点重合,
点E是x轴上一点,连接AE.若AD平分∠OAE,反比例函数y= (k>0,x>0)的
图象经过AE上的两点A,F,且AF=EF,△ABE的面积为18,则k的值为( )
A.6 B.12 C.18 D.24
二、填空题:(本大题6个小题,每小题4分,共24分)请将每小题的答案直接填在答题
卡中对应的横线上.
13.(4分)计算:( ﹣1)0+|﹣2|= .
π14.(4分)一个多边形的内角和等于它的外角和的2倍,则这个多边形的边数是 .
15.(4分)现有四张正面分别标有数字﹣1,1,2,3的不透明卡片,它们除数字外其余
完全相同,将它们背面朝上洗均匀,随机抽取一张,记下数字后放回,背面朝上洗均匀,
再随机抽取一张记下数宇,前后两次抽取的数字分别记为 m,n.则点P(m,n)在第
二象限的概率为 .
16.(4分)如图,在边长为2的正方形ABCD中,对角线AC的中点为O,分别以点A,
C为圆心,以AO的长为半径画弧,分别与正方形的边相交,则图中的阴影部分的面积
为 .(结果保留 )
π
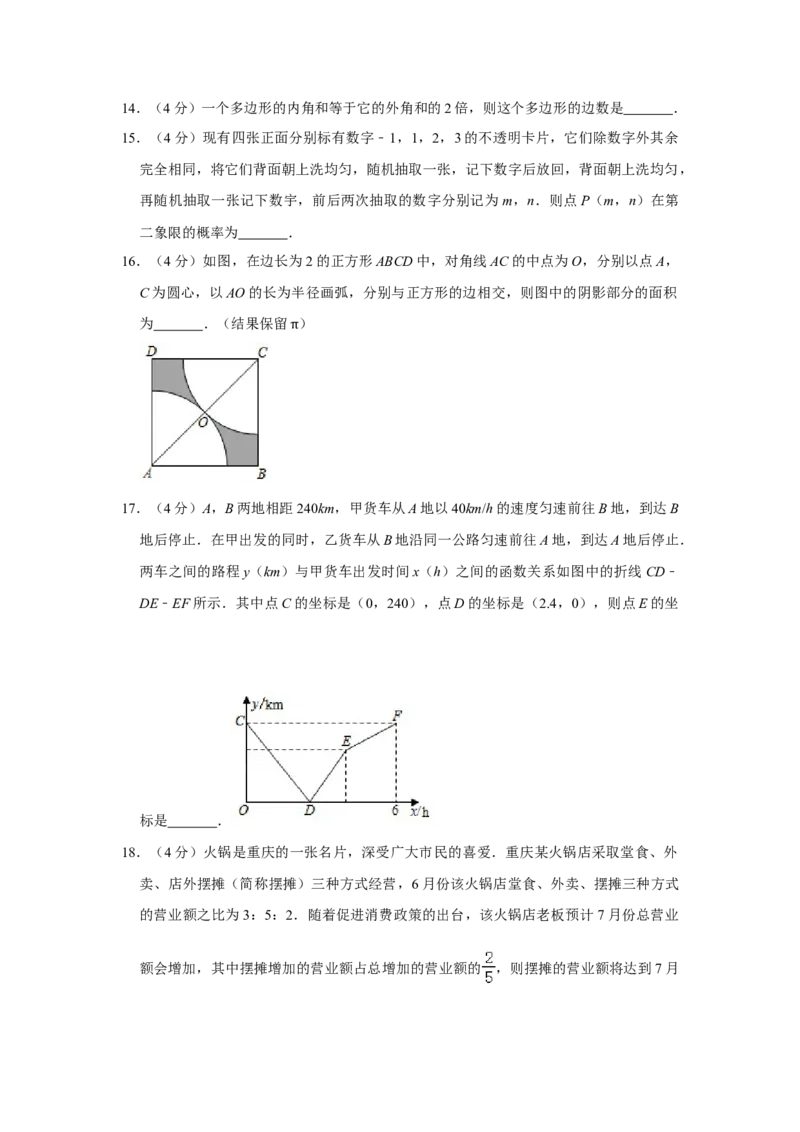
17.(4分)A,B两地相距240km,甲货车从A地以40km/h的速度匀速前往B地,到达B
地后停止.在甲出发的同时,乙货车从B地沿同一公路匀速前往A地,到达A地后停止.
两车之间的路程y(km)与甲货车出发时间x(h)之间的函数关系如图中的折线CD﹣
DE﹣EF所示.其中点C的坐标是(0,240),点D的坐标是(2.4,0),则点E的坐
标是 .
18.(4分)火锅是重庆的一张名片,深受广大市民的喜爱.重庆某火锅店采取堂食、外
卖、店外摆摊(简称摆摊)三种方式经营,6月份该火锅店堂食、外卖、摆摊三种方式
的营业额之比为3:5:2.随着促进消费政策的出台,该火锅店老板预计7月份总营业
额会增加,其中摆摊增加的营业额占总增加的营业额的 ,则摆摊的营业额将达到7月份总营业额的 ,为使堂食、外卖7月份的营业额之比为8:5,则7月份外卖还需增
加的营业额与7月份总营业额之比是 .
三、解答题:(本大题7个小题,每小题10分,共70分)解答时每小题必须给出必要的
演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对
应的位置上.
19.(10分)计算:
(1)(x+y)2+x(x﹣2y);
(2)(1﹣ )÷ .
20.(10分)为了解学生掌握垃圾分类知识的情况,增强学生环保意识.某学校举行了
“垃圾分类人人有责”的知识测试活动,现从该校七、八年级中各随机抽取20名学生
的测试成绩(满分10分,6分及6分以上为合格)进行整理、描述和分析,下面给出了
部分信息.
七年级20名学生的测试成绩为:7,8,7,9,7,6,5,9,10,9,8,5,8,7,6,
7,9,7,10,6.
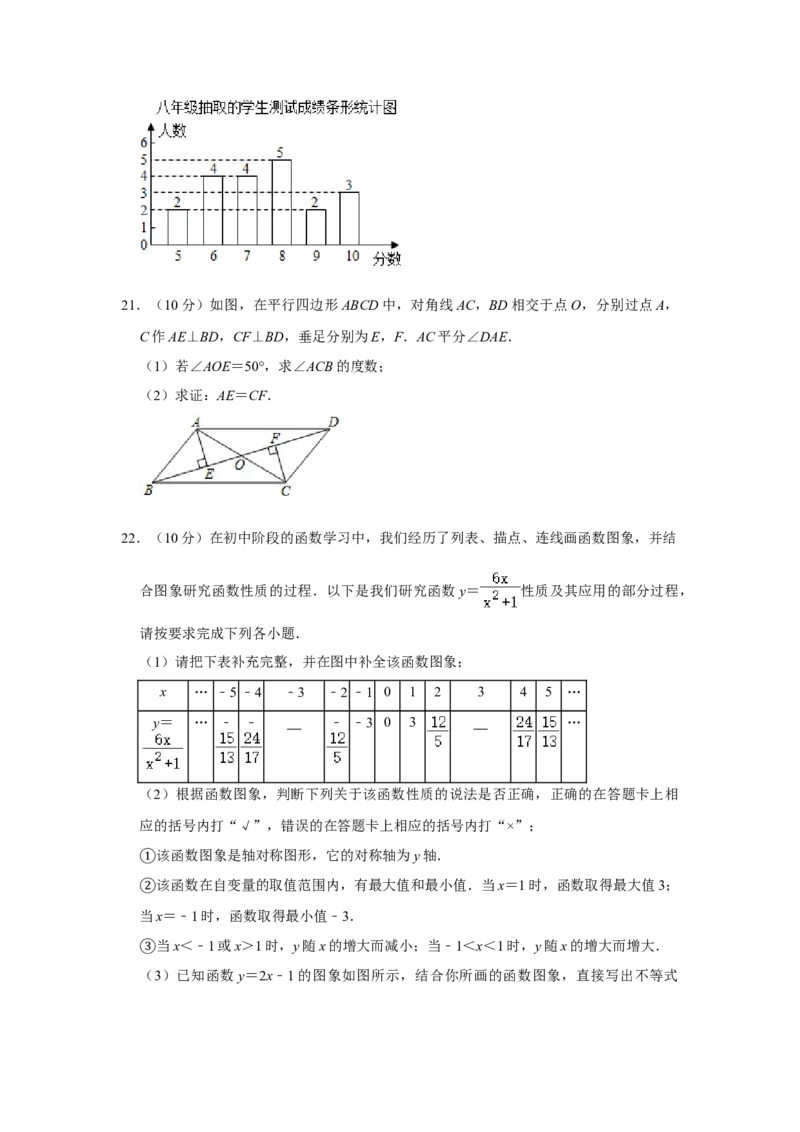
八年级20名学生的测试成绩条形统计图如图:
七、八年级抽取的学生的测试成绩的平均数、众数、中位数、8分及以上人数所占百分
比如下表所示:
年级 平均数 众数 中位数 8分及以上人数所占百分比
七年级 7.5 a 7 45%
八年级 7.5 8 b c
根据以上信息,解答下列问题:
(1)直接写出上述表中的a,b,c的值;
(2)根据上述数据,你认为该校七、八年级中哪个年级学生掌握垃极分类知识较好?
请说明理由(写出一条理由即可);
(3)该校七、八年级共1200名学生参加了此次测试活动,估计参加此次测试活动成绩
合格的学生人数是多少?21.(10分)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,分别过点A,
C作AE⊥BD,CF⊥BD,垂足分别为E,F.AC平分∠DAE.
(1)若∠AOE=50°,求∠ACB的度数;
(2)求证:AE=CF.
22.(10分)在初中阶段的函数学习中,我们经历了列表、描点、连线画函数图象,并结
合图象研究函数性质的过程.以下是我们研究函数y= 性质及其应用的部分过程,
请按要求完成下列各小题.
(1)请把下表补充完整,并在图中补全该函数图象;
x … ﹣5﹣4 ﹣3 ﹣2﹣1 0 1 2 3 4 5 …
y= … ﹣ ﹣ ﹣ ﹣3 0 3 …
(2)根据函数图象,判断下列关于该函数性质的说法是否正确,正确的在答题卡上相
应的括号内打“√”,错误的在答题卡上相应的括号内打“×”;
该函数图象是轴对称图形,它的对称轴为y轴.
①该函数在自变量的取值范围内,有最大值和最小值.当x=1时,函数取得最大值3;
②当x=﹣1时,函数取得最小值﹣3.
当x<﹣1或x>1时,y随x的增大而减小;当﹣1<x<1时,y随x的增大而增大.
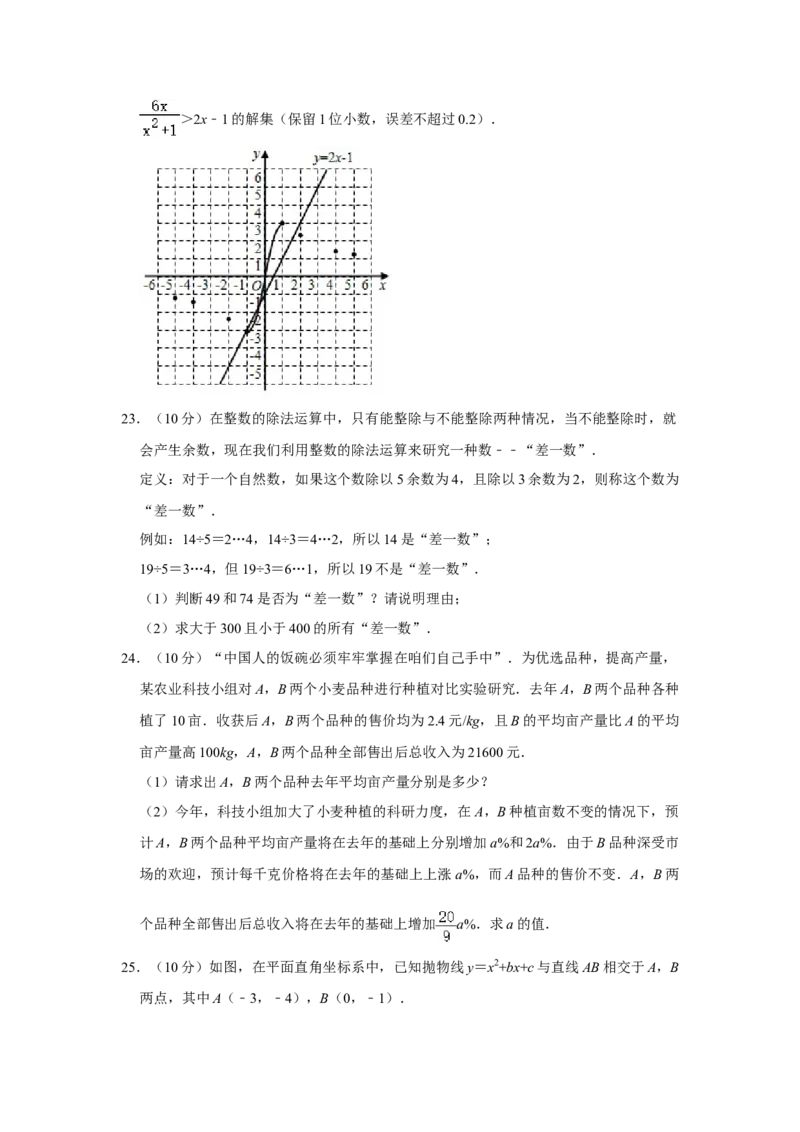
③(3)已知函数y=2x﹣1的图象如图所示,结合你所画的函数图象,直接写出不等式>2x﹣1的解集(保留1位小数,误差不超过0.2).
23.(10分)在整数的除法运算中,只有能整除与不能整除两种情况,当不能整除时,就
会产生余数,现在我们利用整数的除法运算来研究一种数﹣﹣“差一数”.
定义:对于一个自然数,如果这个数除以5余数为4,且除以3余数为2,则称这个数为
“差一数”.
例如:14÷5=2…4,14÷3=4…2,所以14是“差一数”;
19÷5=3…4,但19÷3=6…1,所以19不是“差一数”.
(1)判断49和74是否为“差一数”?请说明理由;
(2)求大于300且小于400的所有“差一数”.
24.(10分)“中国人的饭碗必须牢牢掌握在咱们自己手中”.为优选品种,提高产量,
某农业科技小组对A,B两个小麦品种进行种植对比实验研究.去年A,B两个品种各种
植了10亩.收获后A,B两个品种的售价均为2.4元/kg,且B的平均亩产量比A的平均
亩产量高100kg,A,B两个品种全部售出后总收入为21600元.
(1)请求出A,B两个品种去年平均亩产量分别是多少?
(2)今年,科技小组加大了小麦种植的科研力度,在A,B种植亩数不变的情况下,预
计A,B两个品种平均亩产量将在去年的基础上分别增加a%和2a%.由于B品种深受市
场的欢迎,预计每千克价格将在去年的基础上上涨a%,而A品种的售价不变.A,B两
个品种全部售出后总收入将在去年的基础上增加 a%.求a的值.
25.(10分)如图,在平面直角坐标系中,已知抛物线y=x2+bx+c与直线AB相交于A,B
两点,其中A(﹣3,﹣4),B(0,﹣1).(1)求该抛物线的函数表达式;
(2)点P为直线AB下方抛物线上的任意一点,连接PA,PB,求△PAB面积的最大值;
(3)将该抛物线向右平移2个单位长度得到抛物线y=a x2+b x+c (a ≠0),平移后的
1 1 1 1
抛物线与原抛物线相交于点C,点D为原抛物线对称轴上的一点,在平面直角坐标系中
是否存在点E,使以点B,C,D,E为顶点的四边形为菱形,若存在,请直接写出点E
的坐标;若不存在,请说明理由.
四、解答题:(本大题1个小题,共8分)解答时必须给出必要的演算过程或推理步骤,
画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.
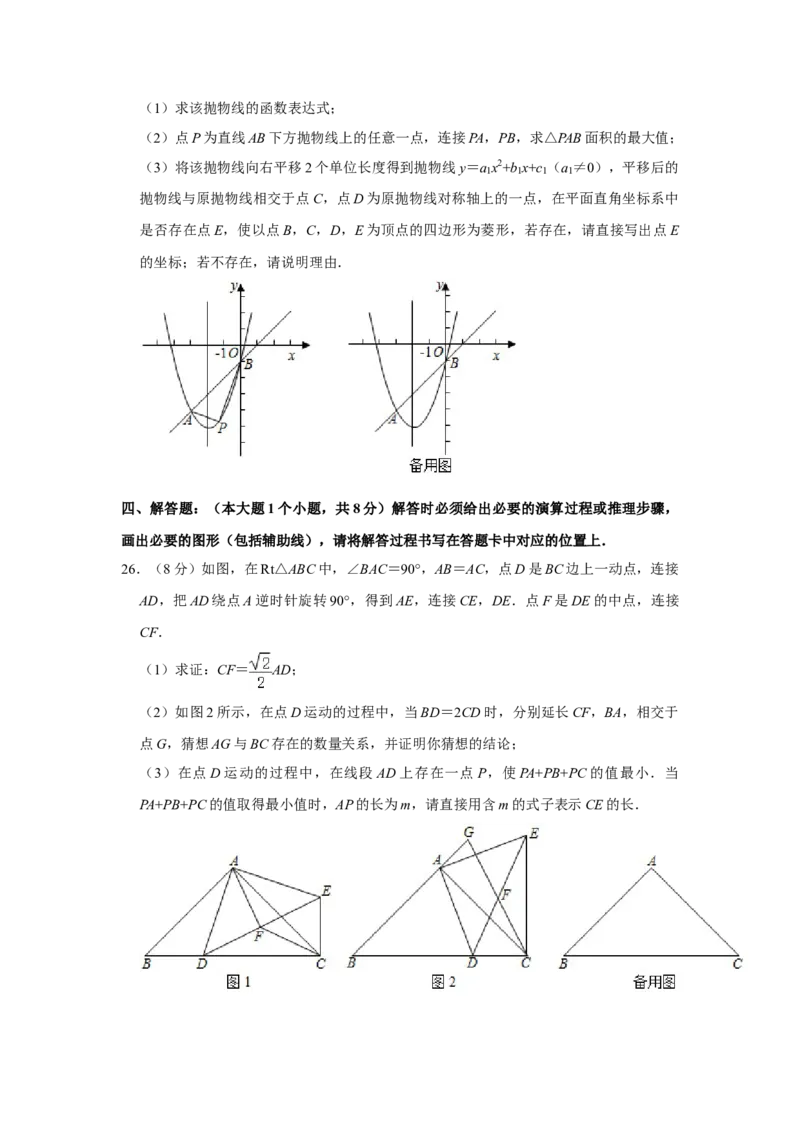
26.(8分)如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D是BC边上一动点,连接
AD,把AD绕点A逆时针旋转90°,得到AE,连接CE,DE.点F是DE的中点,连接
CF.
(1)求证:CF= AD;
(2)如图2所示,在点D运动的过程中,当BD=2CD时,分别延长CF,BA,相交于
点G,猜想AG与BC存在的数量关系,并证明你猜想的结论;
(3)在点D运动的过程中,在线段 AD上存在一点P,使PA+PB+PC的值最小.当
PA+PB+PC的值取得最小值时,AP的长为m,请直接用含m的式子表示CE的长.2020年重庆市中考数学试卷(A卷)
参考答案与试题解析
一、选择题:(本大题12个小题,每小题4分,共48分)在每个小题的下面,都给出了
代号为A、B、C、D的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答
案所对应的方框涂黑.
1.【解答】解:∵﹣3<0<1<2,
∴这四个数中最小的数是﹣3.
故选:A.
2.【解答】解:B、C、D都不是轴对称图形,A是轴对称图形,
故选:A.
3.【解答】解:26000=2.6×104,
故选:C.
4.【解答】解:∵第 个图案中黑色三角形的个数为1,
第 个图案中黑色①三角形的个数3=1+2,
第②个图案中黑色三角形的个数6=1+2+3,
…③…
∴第 个图案中黑色三角形的个数为1+2+3+4+5=15,
故选⑤:B.
5.【解答】解:∵AB是 O的切线,A为切点,
∴∠A=90°, ⊙
∵∠B=20°,
∴∠AOB=90°﹣20°=70°,
故选:D.
6.【解答】解:A. 与 不是同类二次根式,不能合并,此选项计算错误;
B.2与 不是同类二次根式,不能合并,此选项计算错误;
C. × = = ,此选项计算正确;
D.2 与﹣2不是同类二次根式,不能合并,此选项错误;
故选:C.
7.【解答】解:方程两边都乘以6,得:3(x+1)=6﹣2x,
故选:D.8.【解答】解:∵以原点为位似中心,在原点的同侧画△DEF,使△DEF与△ABC成位
似图形,且相似比为2:1,
而A(1,2),C(3,1),
∴D(2,4),F(6,2),
∴DF= =2 .
故选:D.
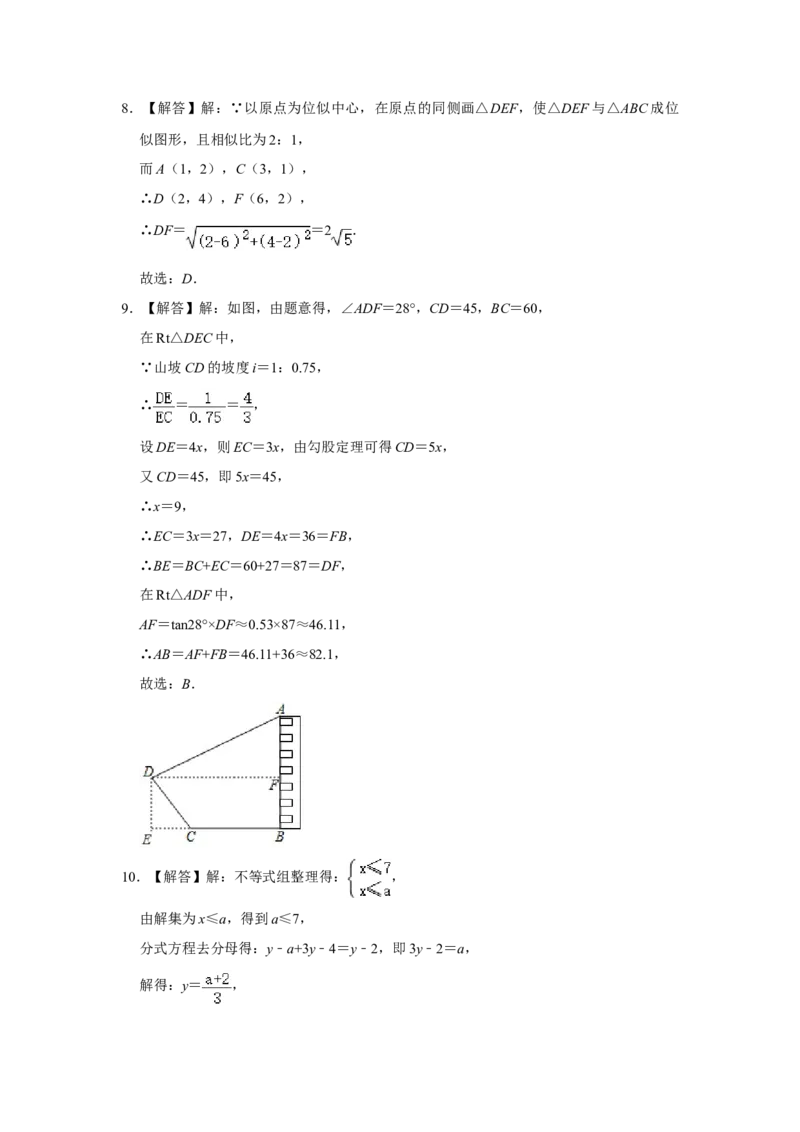
9.【解答】解:如图,由题意得,∠ADF=28°,CD=45,BC=60,
在Rt△DEC中,
∵山坡CD的坡度i=1:0.75,
∴ = = ,
设DE=4x,则EC=3x,由勾股定理可得CD=5x,
又CD=45,即5x=45,
∴x=9,
∴EC=3x=27,DE=4x=36=FB,
∴BE=BC+EC=60+27=87=DF,
在Rt△ADF中,
AF=tan28°×DF≈0.53×87≈46.11,
∴AB=AF+FB=46.11+36≈82.1,
故选:B.
10.【解答】解:不等式组整理得: ,
由解集为x≤a,得到a≤7,
分式方程去分母得:y﹣a+3y﹣4=y﹣2,即3y﹣2=a,
解得:y= ,由y为正整数解,得到a=1,4,7
1×4×7=28,
故选:C.
11.【解答】解:∵DG=GE,
∴S△ADG =S△AEG =2,
∴S△ADE =4,
由翻折可知,△ADB≌△ADE,BE⊥AD,
∴S△ABD =S△ADE =4,∠BFD=90°,
∴ •(AF+DF)•BF=4,
∴ •(3+DF)•2=4,
∴DF=1,
∴DB= = = ,
设点F到BD的距离为h,则有 •BD•h= •BF•DF,
∴h= ,
故选:B.
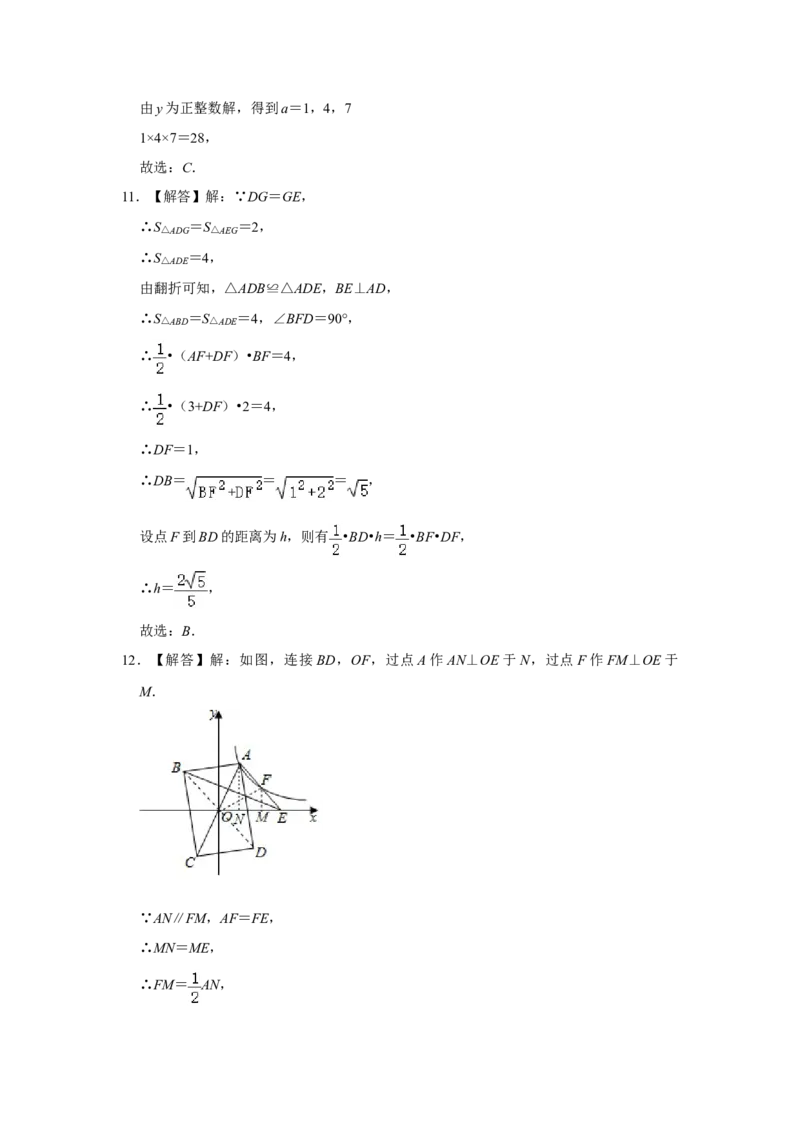
12.【解答】解:如图,连接 BD,OF,过点A作AN⊥OE于N,过点F作FM⊥OE于
M.
∵AN∥FM,AF=FE,
∴MN=ME,
∴FM= AN,∵A,F在反比例函数的图象上,
∴S△AON =S△FOM = ,
∴ •ON•AN= •OM•FM,
∴ON= OM,
∴ON=MN=EM,
∴ME= OE,
∴S△FME = S△FOE ,
∵AD平分∠OAE,
∴∠OAD=∠EAD,
∵四边形ABCD是矩形,
∴OA=OD,
∴∠OAD=∠ODA=∠DAE,
∴AE∥BD,
∴S△ABE =S△AOE ,
∴S△AOE =18,
∵AF=EF,
∴S△EOF = S△AOE =9,
∴S△FME = S△EOF =3,
∴S△FOM =S△FOE ﹣S△FME =9﹣3=6= ,
∴k=12.
故选:B.
二、填空题:(本大题6个小题,每小题4分,共24分)请将每小题的答案直接填在答题
卡中对应的横线上.
13.【解答】解:( ﹣1)0+|﹣2|=1+2=3,
故答案为:3. π14.【解答】解:设这个多边形的边数为n,依题意,得:
(n﹣2)•180°=2×360°,
解得n=6.
故答案为:6.
15.【解答】解:画树状图为:
共有16种等可能的结果数,其中点P(m,n)在第二象限的结果数为3,
所以点P(m,n)在第二象限的概率= .
故答案为 .
16.【解答】解:∵四边形ABCD为正方形,
∴AB=BC=2,∠DAB=∠DCB=90°,
由勾股定理得,AC= =2 ,
∴OA=OC= ,
∴图中的阴影部分的面积=22﹣ ×2=4﹣ ,
π
故答案为:4﹣ .
17.【解答】解:π根据题意可得,乙货车的速度为:240÷2.4﹣40=60(40km/h),
∴乙货车从B地到A地所用时间为:240÷60=4(小时),
当乙货车到底A地时,甲货车行驶的路程为:40×4=160(千米),
∴点E的坐标是(4,160).
故答案为:(4,160).
18.【解答】解:设6月份堂食、外卖、摆摊三种方式的营业额为3a,5a,2a,设7月份
总的增加营业额为5x,摆摊增加的营业额为2x,7月份总营业额20b,摆摊7月份的营
业额为7b,堂食7月份的营业额为8b,外卖7月份的营业额为5b,
由题意可得: ,解得: ,
∴7月份外卖还需增加的营业额与7月份总营业额之比=(5b﹣5a):20b=1:8,
故答案为:1:8.
三、解答题:(本大题7个小题,每小题10分,共70分)解答时每小题必须给出必要的
演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对
应的位置上.
19.【解答】解:(1)(x+y)2+x(x﹣2y),
=x2+2xy+y2+x2﹣2xy,
=2x2+y2;
(2)(1﹣ )÷ ,
=( ﹣ )× ,
= × ,
= .
20.【解答】解:(1)∵七年级20名学生的测试成绩为:7,8,7,9,7,6,5,9,
10,9,8,5,8,7,6,7,9,7,10,6,
∴a=7,
由条形统计图可得,b=(7+8)÷2=7.5,
c=(5+2+3)÷20×100%=50%,
即a=7,b=7.5,c=50%;
(2)八年级学生掌握垃极分类知识较好,理由:八年级的 8分及以上人数所占百分比
大于七年级,故八年级学生掌握垃极分类知识较好;
(3)∵从调查的数据看,七年级2人的成绩不合格,八年级2人的成绩不合格,
∴参加此次测试活动成绩合格的学生有1200× =1080(人),
即参加此次测试活动成绩合格的学生有1080人.
21.【解答】(1)解:∵AE⊥BD,∴∠AEO=90°,
∵∠AOE=50°,
∴∠EAO=40°,
∵CA平分∠DAE,
∴∠DAC=∠EAO=40°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∠ACB=∠DAC=40°,
(2)证明:∵四边形ABCD是平行四边形,
∴OA=OC,
∵AE⊥BD,CF⊥BD,
∴∠AEO=∠CFO=90°,
∵∠AOE=∠COF,
∴△AEO≌△CFO(AAS),
∴AE=CF.
22.【解答】解:(1)补充完整下表为:
x … ﹣5﹣4 ﹣3 ﹣2﹣1 0 1 2 3 4 5 …
y= … ﹣ ﹣ ﹣ ﹣3 0 3 …
﹣
画出函数的图象如图:
;
(2)根据函数图象:该函数图象是轴对称图形,它的对称轴为y轴,说法错误;
①该函数在自变量的取值范围内,有最大值和最小值.当x=1时,函数取得最大值3;
②当x=﹣1时,函数取得最小值﹣3,说法正确;
当x<﹣1或x>1时,y随x的增大而减小;当﹣1<x<1时,y随x的增大而增大,
③说法正确.
(3)由图象可知:不等式 >2x﹣1的解集为x<﹣1或﹣0.3<1.8.
23.【解答】解:(1)49÷5=9…4,但49÷3=16…1,所以49不是“差一数”;
74÷5=14…4,74÷3=24…2,所以74是“差一数”.
(2)大于300且小于400的数除以5余数为4的有304,309,314,319,324,329,
334,339,344,349,354,359,364,369,374,379,384,389,394,399,
其中除以3余数为2的有314,327,344,359,374,389.
故大于300且小于400的所有“差一数”有314,327,344,359,374,389.
24.【解答】解:(1)设A、B两个品种去年平均亩产量分别是x千克和y千克;
根据题意得, ,
解得: ,
答:A、B两个品种去年平均亩产量分别是400千克和500千克;
(2)2.4×400×10(1+a%)+2.4(1+a%)×500×10(1+2a%)=21600(1+ a%),
解得:a=0.1,
答:a的值为0.1.
25.【解答】解:(1)将点A、B的坐标代入抛物线表达式得 ,解得 ,
故抛物线的表达式为:y=x2+4x﹣1;
(2)设直线AB的表达式为:y=kx+t,则 ,解得 ,
故直线AB的表达式为:y=x﹣1,
过点P作y轴的平行线交AB于点H,设点P(x,x2+4x﹣1),则H(x,x﹣1),
△PAB面积S= ×PH×(x ﹣x )= (x﹣1﹣x2﹣4x+1)×(0+3)=﹣ x2﹣ x,
B A
∵ <0,故S有最大值,当x=﹣ 时,S的最大值为 ;
(3)抛物线的表达式为:y=x2+4x﹣1=(x+2)2﹣5,
则平移后的抛物线表达式为:y=x2﹣5,
联立上述两式并解得: ,故点C(﹣1,﹣4);
设点D(﹣2,m)、点E(s,t),而点B、C的坐标分别为(0,﹣1)、(﹣1,﹣
4);
当BC为菱形的边时,
①点C向右平移1个单位向上平移3个单位得到B,同样D(E)向右平移1个单位向上平
移3个单位得到E(D),
即﹣2+1=s且m+3=t 或﹣2﹣1=s且m﹣3=t ,
当点D在E的下方时,①则BE=BC,即s2+(t+1)② 2=12+32 ,
当点D在E的上方时,则BD=BC,即22+(m+1)2=12+3③ 2 ,
④联立 并解得:s=﹣1,t=2或﹣4(舍去﹣4),故点E(﹣1,3);
联立
①③
并解得:s=1,t=﹣4± ,故点E(1,﹣4 )或(1,﹣4﹣ );
当②BC④为菱形的的对角线时,
②则由中点公式得:﹣1=s﹣2且﹣4﹣1=m+t ,
此时,BD=BE,即22+(m+1)2=s2+(t+1)⑤ 2 ,
联立 并解得:s=1,t=﹣3, ⑥
故点⑤E(⑥1,﹣3),
综上,点E的坐标为:(﹣1,2)或(1,﹣4 )或(1,﹣4﹣ )或(1,﹣
3).
四、解答题:(本大题1个小题,共8分)解答时必须给出必要的演算过程或推理步骤,
画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.
26.【解答】证明:(1)∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵把AD绕点A逆时针旋转90°,得到AE,
∴AD=AE,∠DAE=90°=∠BAC,
∴∠BAD=∠CAE,DE= AD,
又∵AB=AC,
∴△BAD≌△CAE(SAS),
∴∠ABD=∠ACE=45°,
∴∠BCE=∠BCA+∠ACE=90°,
∵点F是DE的中点,
∴CF= DE= AD;
(2)AG= BC,
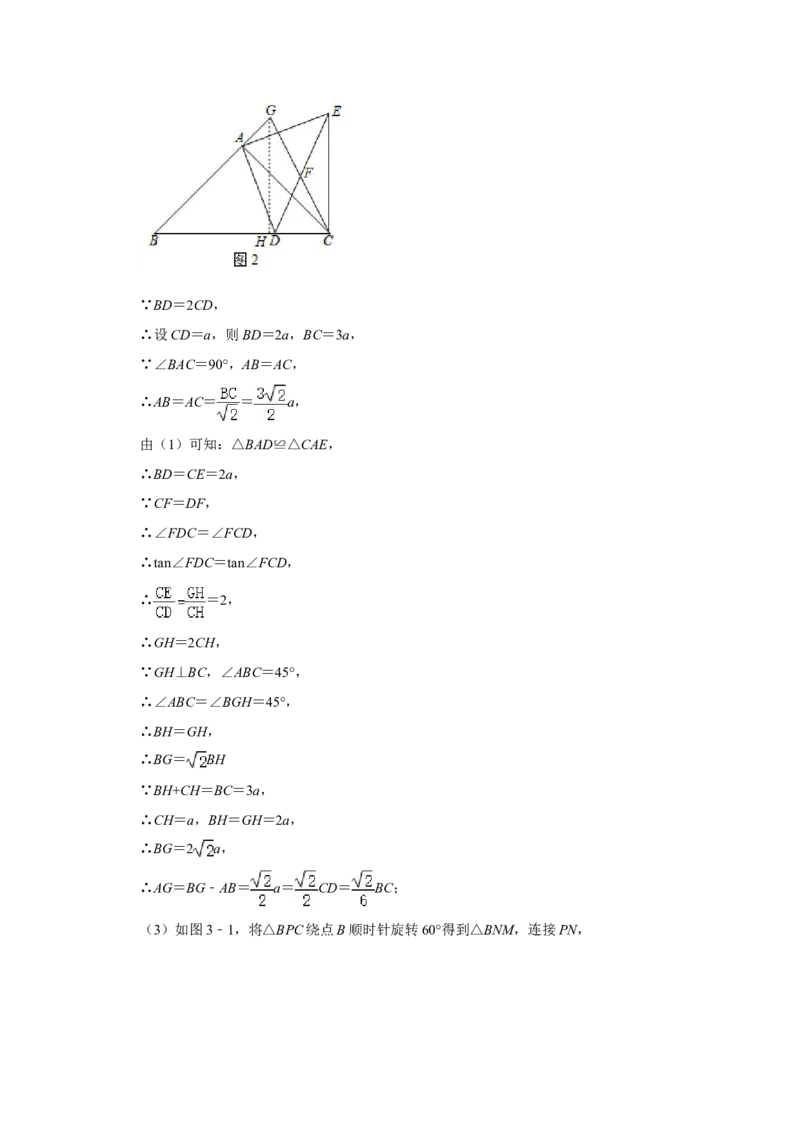
理由如下:如图2,过点G作GH⊥BC于H,∵BD=2CD,
∴设CD=a,则BD=2a,BC=3a,
∵∠BAC=90°,AB=AC,
∴AB=AC= = a,
由(1)可知:△BAD≌△CAE,
∴BD=CE=2a,
∵CF=DF,
∴∠FDC=∠FCD,
∴tan∠FDC=tan∠FCD,
∴ =2,
∴GH=2CH,
∵GH⊥BC,∠ABC=45°,
∴∠ABC=∠BGH=45°,
∴BH=GH,
∴BG= BH
∵BH+CH=BC=3a,
∴CH=a,BH=GH=2a,
∴BG=2 a,
∴AG=BG﹣AB= a= CD= BC;
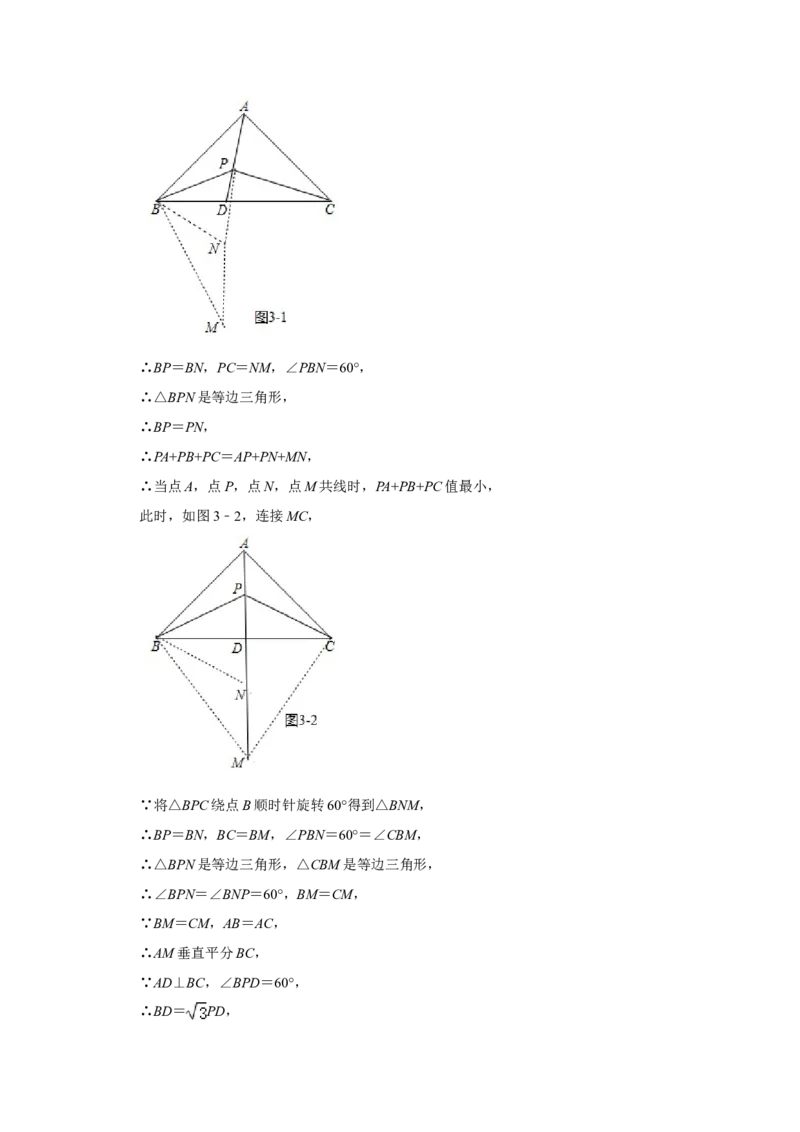
(3)如图3﹣1,将△BPC绕点B顺时针旋转60°得到△BNM,连接PN,∴BP=BN,PC=NM,∠PBN=60°,
∴△BPN是等边三角形,
∴BP=PN,
∴PA+PB+PC=AP+PN+MN,
∴当点A,点P,点N,点M共线时,PA+PB+PC值最小,
此时,如图3﹣2,连接MC,
∵将△BPC绕点B顺时针旋转60°得到△BNM,
∴BP=BN,BC=BM,∠PBN=60°=∠CBM,
∴△BPN是等边三角形,△CBM是等边三角形,
∴∠BPN=∠BNP=60°,BM=CM,
∵BM=CM,AB=AC,
∴AM垂直平分BC,
∵AD⊥BC,∠BPD=60°,
∴BD= PD,∵AB=AC,∠BAC=90°,AD⊥BC,
∴AD=BD,
∴ PD=PD+AP,
∴PD= m,
∴BD= PD= m,
由(1)可知:CE=BD= m.