文档内容
西宁市普通高中2023—2024学年第一学期期末联考测试卷
高三年级数学理科学科参考答案:
1.D 2.D 3.A 4.A 5.C 6.D 7.B 8.C 9.D 10.C 11.C 12.C
13. 14. 15.14或23 16.
17.(1)由题意可得, ,且 ,-------------1分
则 ,所以 ,-------------2分
所以 ,将点 代入,可得 ,
即 ,解得 ,且 ,则 ,----------5分
所以 .-----------6分
(2)由(1)可得 ,
令 , ,------------8分
解得 , ,------------10分
18(1)∵四边形ABCD中 , , , , ,
M为AD的中点,且 ,
∴四边形ABNM为正方形,且边长为1,
答案第1页,共2页
学科网(北京)股份有限公司∴题图2中,四边形EMNF是边长为1的正方形,故
又 , ,∴ ,----------1分
∴ ,又 , , 平面MDCN, 平面MDCN,
∴ 平面MDCN,-----------2分
∵ 平面MDCN,∴ ,
易知 ,∴ ,∴ ,
又 , 平面 , 平面 ,∴ 平面 ;-----------4分
(2)解法一:由(1)知 平面MDCN,又 ,
以N为坐标原点,建立空间直角坐标系,如图所示,-----------5分
则 , , , ,
∴ , , ,------6分
设平面FND的法向量为 ,则 ,
令 ,令 ,则 ,∴ ,--------------8分
答案第2页,共2页设平面PND的法向量为 ,则 ,
令 ,则 , ,∴ ,---------------10分
∴ ,------------11分
∴ ,------------12分
∴二面角 的正弦值为 .
解法二:如图,取NC的中点O,连接PO,则 ,
∴ 平面MDCN,
∵ 平面MDCN,∴ ,
过O作 ,垂足为H,连接PH,则 就是二面角 的平面角,
又 , ,∴ ,∴ ,
∵ 平面MDCN, 平面FND,∴平面 平面MDCN,
∴二面角 的正弦值为 .
19.(1)设等差数列 的公差为 ,
答案第3页,共2页
学科网(北京)股份有限公司由题意,得 ,------------2分
解得 或 ,--------------4分
所以 或 ;-------------6分
(2)当 时, ,-----------7分
此时 ;----------9分
当 时, ,-----------10分
20.此时 .------------12分所
以 的单调增区间为 .-------------12分.解(1)设双曲线方程为
,将 代入可得 ,
所以双曲线方程为 .-------------2分
双曲线的顶点为 ,焦点为 ,--------------------1分
所以椭圆的顶点为 ,焦点为 ,所以 ,---------------1分
答案第4页,共2页所以椭圆B的方程为 .-----------------4分
(3)证明:设 ,--------------5分
由 ,-------------------7分
所以 ,-----------------------9分
同理可得 ,-----------------11分
所以 .------------------12分
21.(1) ,----------1分
当 时, ,
由 得 或 ,------------2分
所以函数 的单调递增区间为 和 .----------------3分
(2) .
当 时,令 ,得 ,
答案第5页,共2页
学科网(北京)股份有限公司则当 时, ,当 时, ,
所以函数 仅有唯一的极小值点 ,
此时 ,显然符合题意.---------------5分
当 时,令 ,得 或 ,
若 ,即 ,则 ,
此时 单调递增,无极值点,不符合题意;----------------------7分
若 ,即 ,
则当 时, ,
当 时, ,
所以函数 的极小值点 ,
由 得 ,所以 ;----------------------9分
若 ,即 ,
则当 时, ,
当 时, ,
所以函数 的极小值点 ,--------------------------11分
答案第6页,共2页由 得 .
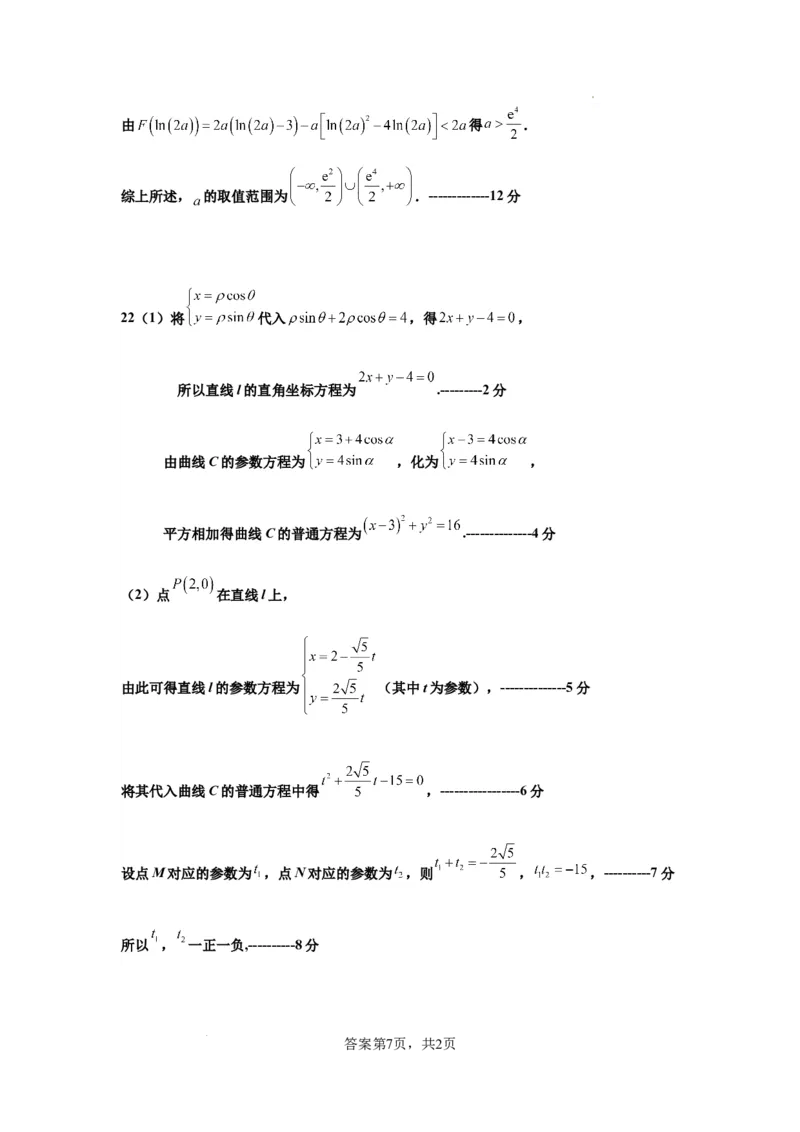
综上所述, 的取值范围为 .-------------12分
22(1)将 代入 ,得 ,
所以直线l的直角坐标方程为 .---------2分
由曲线C的参数方程为 ,化为 ,
平方相加得曲线C的普通方程为 .--------------4分
(2)点 在直线l上,
由此可得直线l的参数方程为 (其中t为参数),--------------5分
将其代入曲线C的普通方程中得 ,-----------------6分
设点M对应的参数为 ,点N对应的参数为 ,则 , ,----------7分
所以 , 一正一负,----------8分
答案第7页,共2页
学科网(北京)股份有限公司所以 .-----------9分
所以 = .-------------10分
23(1)当 时, 即
的解集是下列三个不等式组的解集的并集:
① ② ③ -------------2分
解①得:
解②得:
解③知,适合该不等式组的实数 不存在
不等式 的解集为 ---4分---------
(2)由绝对值的三角形不等式,得:
-----------6分
又 ------------8分
对任意实数 ,不等式 在 上恒成立.-------------10分
答案第8页,共2页