文档内容
绝密★启用前
2024 年高考押题预测卷 01【新九省卷】
数 学
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用
橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共58分)
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要
求的。
1.已知复数 ,则 ( )
A. B. C. D.
【答案】A
【解析】由 得 ,故 ,故选A
2.为了了解学生们的身体状况,某学校决定采用分层抽样的方法,从高一、高二、高三三个年级共抽取100
人进行各项指标测试.已知高三年级有500人,高二年级有700人,高一年级有800人,则高三年级抽
取的人数为( )
A.30 B.25 C.20 D.15
【答案】B
【解析】根据分层抽样的性质可知:
高三年级抽取的人数为 ,故选B
3.已知 , ,若 ,则 ( )
1
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司A.1 B. C. D.
【答案】A
【解析】因为 , , ,
所以 ,解得 ,故选A.
4.若 ,则 ( )
A. B. C. D.
【答案】D
【解析】因为 ,所以 ,所以 ,
所以 .故选:D
5.双曲线 的左、右焦点分别为 ,且 的一条渐近线与直线
平行,则双曲线 的标准方程为( )
A. B. C. D.
【答案】A
【解析】由题意知 ,解得 ,故双曲线 的标准方程为 .故选A.
6.我国元代瓷器元青花团菊花纹小盏如图所示,撇口,深弧壁,圈足微微外撇,底心有一小乳突.器身施
白釉,以青花为装饰,釉质润泽,底足露胎,胎质致密.碗内口沿饰有一周回纹,内底心书有一文字,
碗外壁绘有一周缠枝团菊纹,下笔流畅,纹饰洒脱.该元青花团菊花纹小盏口径8.4厘米,底径2.8厘米,
2
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司高4厘米,它的形状可近似看作圆台,则其侧面积约为(单位:平方厘米)( )(附:
)
A. B. C. D.
【答案】B
【解析】设该圆台的上底面、下底面的半径分别为 ,
由题意可知: ,则圆台的母线长 ,
所以其侧面积为 .
故选:B.
7.已知 为坐标原点,直线 与圆 相交于 , 两点,则 ( )
A.4 B.6 C.8 D.10
【答案】C
【解析】圆 即 ,圆心为 ,半径 ,
又直线 ,令 ,则 ,即直线 恒过点 ,即直线恒过圆心,
又直线 与圆 相交于 , 两点,
所以 ,
所以
.
故选:C
3
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司8.在同一平面上有相距14公里的 两座炮台, 在 的正东方.某次演习时, 向西偏北 方向发射炮
弹, 则向东偏北 方向发射炮弹,其中 为锐角,观测回报两炮弹皆命中18公里外的同一目标,接
着 改向向西偏北 方向发射炮弹,弹着点为18公里外的点 ,则 炮台与弹着点 的距离为
( )
A.7公里 B.8公里 C.9公里 D.10公里
【答案】D
【解析】依题意设炮弹第一次命中点为 ,则 , ,
, ,
在 中 ,
即 ,解得 ,
所以 ,又 为锐角,解得 (负值舍去),
在 中
,
所以 ,即 炮台与弹着点 的距离为 公里.
故选:D
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部
选对的得6分,部分选对的得部分分,有选错的得0分.
9.袋子中有6个相同的球,分别标有数字1,2,3,4,5,6,从中随机取出两个球,设事件 “取出的
球的数字之积为奇数”,事件 “取出的球的数字之积为偶数”,事件 “取出的球的数字之和为
4
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司偶数”,则( )
A.事件 与 是互斥事件 B.事件 与 是对立事件
C.事件 与 是互斥事件 D.事件 与 相互独立
【答案】AB
【解析】对于AB:取出的球的数字之积为奇数和取出的球的数字之积为偶数不可能同时发生,且必有
一个发生,故事件 与 是互斥事件,也是对立事件,AB正确;
对于C:如果取出的数为 ,则事件 与事件 均发生,不互斥,C错误;
对于D: ,
则 ,即事件 与 不相互独立,D错误;
故选:AB.
10.已知函数 的部分图象如图所示,则( )
A.
B. 的图象过点
C.函数 的图象关于直线 对称
D.若函数 在区间 上不单调,则实数 的取值范围是
【答案】BCD
5
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司【解析】A:设该函数的最小正周期为 ,则有 ,
即 ,由函数的图象可知: ,即 ,
由图象可知: ,
所以 ,因此本选项不正确;
B: ,
所以本选项正确;
C:因为 ,
,
所以 ,
所以函数 的图象关于直线 对称,因此本选项正确;
D:
当 时,
,
当 ,
6
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司,
当函数 在区间 上不单调时,
则有 ,
故选:BCD
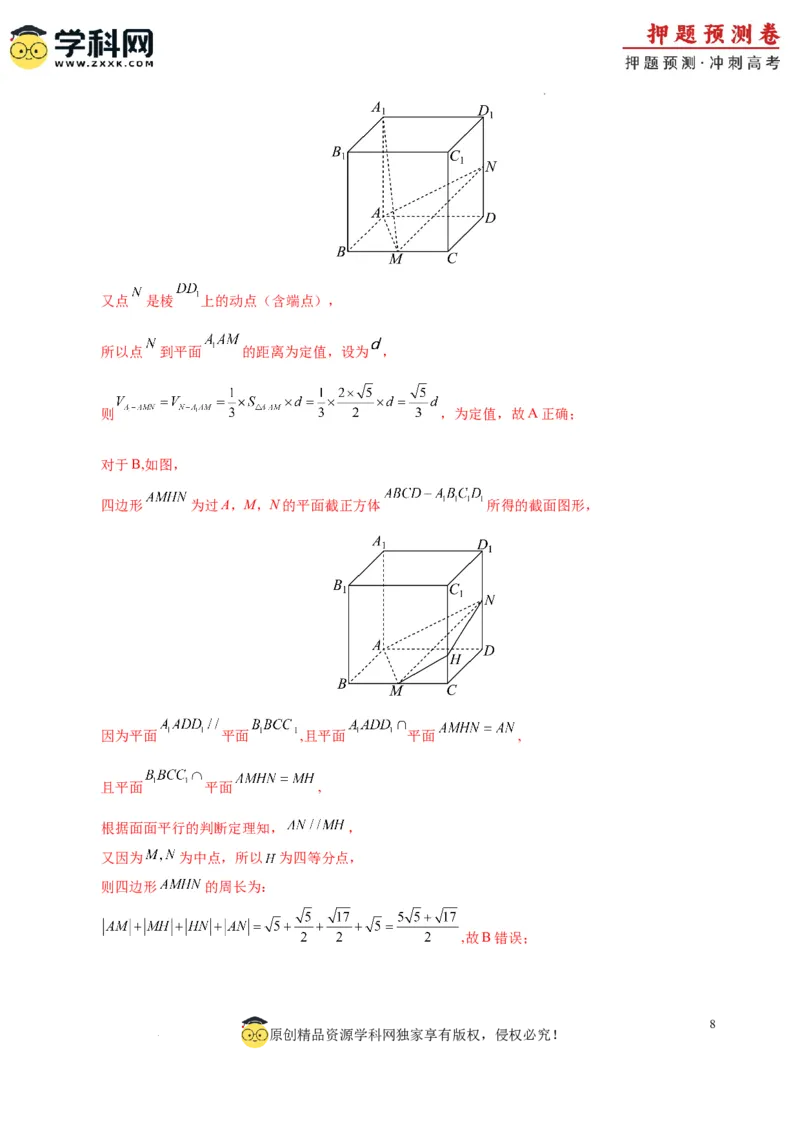
11.如图,在棱长为2的正方体 中, 是棱BC的中点, 是棱 上的动点(含端点),
则下列说法中正确的是( )
A.三棱锥 的体积为定值
B.若 是棱 的中点,则过A,M,N的平面截正方体 所得的截面图形的周长为
C.若 是棱 的中点,则四面体 的外接球的表面积为
D.若CN与平面 所成的角为 ,则
【答案】AD
【解析】对于A,连接 ,因为 ,
平面 , 平面 ,
所以 平面 ,
7
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司又点 是棱 上的动点(含端点),
所以点 到平面 的距离为定值,设为 ,
则 ,为定值,故A正确;
对于B,如图,
四边形 为过A,M,N的平面截正方体 所得的截面图形,
因为平面 平面 ,且平面 平面 ,
且平面 平面 ,
根据面面平行的判断定理知, ,
又因为 为中点,所以 为四等分点,
则四边形 的周长为:
,故B错误;
8
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司对于C,如图所示,连接 ,取 的中点为 ,
连接 ,设 外接圆圆心为 ,外接球球心为 ,
连接 ,则 ,
在 中,设其外接圆半径为 ,
由正弦定理知, ,
所以 ,即 ,
依题易得 ,故 ,
弦 所对的圆周角相等,故 四点共圆,则 ,
设外接球半径为 ,过 作 ,交 于 ,
则在 中, ,
即 ,①
在 中, ,即 ,②
联立①②,解得 ,
9
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司故外接球的表面积为 ,故C错误;
对于D,以 为坐标原点,建立如下图所示空间直角坐标系,
则 ,
则 ,
设平面 的法向量 ,
则 ,
令 ,则 ,故 ,
则 ,
,
当 时, ,
当 时,
,
1
原创精品资源学科网独家享有版权,侵权必究!
0
学科网(北京)股份有限公司当且仅当 时等号成立,
又 ,
综上可知, ,故D正确,
故选:AD.
第二部分(非选择题 共92分)
三、填空题:本题共3小题,每小题5分,共15分。
12.已知集合 ,若 ,则 的取值范围是 .
【答案】
【解析】由 ,得 ,解得 ,
所以 .
因为 ,
所以 或 ,解得 或 ,
所以 的取值范围是 .
13.已知椭圆 的一个焦点的坐标为 ,一条切线的方程为 ,则 的离
心率 .
【答案】
【解析】联立直线与椭圆方程 ,可得 ,
由 为椭圆切线,则有 ,
化简得 ,又 ,故 ,
1
原创精品资源学科网独家享有版权,侵权必究!
1
学科网(北京)股份有限公司又椭圆的一个焦点的坐标为 ,故有 ,
则 ,故 ,则 .
14.关于 的不等式 恒成立,则 的最小值为 .
【答案】
【解析】令 ,则 ,
当 时, ,当 时, ,
所以函数 在 上单调递减,在 上单调递增,
所以 ,所以 ,
由 ,得 ,
而 ,
令 ,
则 ,所以 ,
若 ,
如图作出函数 的图象,
由函数图象可知,方程 有唯一实数根 ,
即 ,
1
原创精品资源学科网独家享有版权,侵权必究!
2
学科网(北京)股份有限公司由 ,得 ,
即 ,
当 时, ,即 ,
又 , ,所以 ,
所以 不成立,
即当 时, 不恒成立,
综上所述, 的最小值为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步棸。
15.(本小题满分13分)为促进全民阅读,建设书香校园,某校在寒假面向全体学生发出“读书好、读好
书、好读书”的号召,并开展阅读活动.开学后,学校统计了高一年级共1000名学生的假期日均阅读
时间(单位:分钟),得到了如下所示的频率分布直方图,若前两个小矩形的高度分别为0.0075,
0.0125,后三个小矩形的高度比为3:2:1.
(1)根据频率分布直方图,估计高一年级1000名学生假期日均阅读时间的平均值(同一组中的数据用
该组区间的中点值为代表);
(2)开学后,学校从高一日均阅读时间不低于60分钟的学生中,按照分层抽样的方式,抽取6名学生
作为代表分两周进行国旗下演讲,假设第一周演讲的3名学生日均阅读时间处于[80,100)的人数记
为 ,求随机变量 的分布列与数学期望.
【解】(1)由题知:各组频率分别为:0.15,0.25,0.3,0.2,0.1,
日均阅读时间的平均数为:
(分钟)
1
原创精品资源学科网独家享有版权,侵权必究!
3
学科网(北京)股份有限公司(2)由题意,在[60,80),[80,100),[100,120]三组分别抽取3,2,1人
的可能取值为:0,1,2
则
所以 的分布列为:
0 1 2
16.(本小题满分15分)如图,在三棱柱 中, 与 的距离为 , ,
.
(1)证明:平面 平面ABC;
(2)若点N在棱 上,求直线AN与平面 所成角的正弦值的最大值.
【解】(1)取棱 中点D,连接 ,因为 ,所以
因为三棱柱 ,所以 ,
1
原创精品资源学科网独家享有版权,侵权必究!
4
学科网(北京)股份有限公司所以 ,所以
因为 ,所以 , ;
因为 , ,所以 ,所以 ,
同理 ,
因为 ,且 , 平面 ,所以 平面 ,
因为 平面 ,
所以平面 平面 ;
(2)取 中点O,连接 ,取 中点P,连接 ,则 ,
由(1)知 平面 ,所以 平面
因为 平面 , 平面 ,
所以 , ,
因为 ,则
以O为坐标原点, , , 所在的直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系
,
则 , , , ,
可设点 , ,
, , ,
设面 的法向量为 ,得 ,
1
原创精品资源学科网独家享有版权,侵权必究!
5
学科网(北京)股份有限公司取 ,则 , ,所以
设直线 与平面 所成角为 ,
则
若 ,则 ,
若 ,则 ,
当且仅当 ,即 时,等号成立,
所以直线 与平面 所成角的正弦值的最大值 .
17.(本小题满分15分)已知函数 .
(1)当 时,求 的单调区间;
(2)讨论 极值点的个数.
【解】(1)当 时, 定义域为 ,
1
原创精品资源学科网独家享有版权,侵权必究!
6
学科网(北京)股份有限公司又 ,
所以 ,
由 ,解得 ,此时 单调递增;
由 ,解得 ,此时 单调递减,
所以 的单调递增区间为 ,单调递减区间为 .
(2)函数 的定义域为 ,
由题意知, ,
当 时, ,所以 在 上单调递增,
即 极值点的个数为 个;
当 时,易知 ,
故解关于 的方程 得, , ,
所以 ,
又 , ,
所以当 时, ,即 在 上单调递增,
当 时, ,即 在 上单调递减,
即 极值点的个数为 个.
综上,当 时, 极值点的个数为 个;当 时, 极值点的个数为 个.
18.(本小题满分17分)设抛物线 ,过焦点 的直线与抛物线 交于点 ,
1
原创精品资源学科网独家享有版权,侵权必究!
7
学科网(北京)股份有限公司.当直线 垂直于 轴时, .
(1)求抛物线 的标准方程.
(2)已知点 ,直线 , 分别与抛物线 交于点 , .
①求证:直线 过定点;
②求 与 面积之和的最小值.
【解】(1)由题意,当直线 垂直于 轴时, ,代入抛物线方程得 ,则 ,
所以 ,即 ,所以抛物线 .
(2)(i)设 , ,直线 ,
与抛物线 联立,得 ,因此 , .
设直线 ,与抛物线 联立,得 ,
因此 , ,则 .同理可得 .
所以 .
因此直线 ,由对称性知,定点在 轴上,
令 得,
1
原创精品资源学科网独家享有版权,侵权必究!
8
学科网(北京)股份有限公司,
所以直线 过定点 .
(ii)因为 ,
,
所以 ,
当且仅当 时取到最小值 .
19.(本小题满分17分)给定整数 ,由 元实数集合 定义其相伴数集 ,如
果 ,则称集合S为一个 元规范数集,并定义S的范数 为其中所有元素绝对值之和.
(1)判断 、 哪个是规范数集,并说明理由;
(2)任取一个 元规范数集S,记 、 分别为其中最小数与最大数,求证: ;
(3)当 遍历所有2023元规范数集时,求范数 的最小值.
注: 、 分别表示数集 中的最小数与最大数.
【解】(1)对于集合A:因为 ,所以集合A不是规范数集;
对于集合B:因为 ,
又 , , , , , ,
所以B相伴数集 ,即 ,故集合B是规范数集.
1
原创精品资源学科网独家享有版权,侵权必究!
9
学科网(北京)股份有限公司(2)不妨设集合S中的元素为 ,即 ,
因为S为规范数集,则 ,则 ,且 ,使得 ,
当 时,
则 ,
当且仅当 且 时,等号成立;
当 时,
则 ,
当且仅当 且 时,等号成立;
当 时,
则 ,
当且仅当 时,等号成立;
综上所述: .
(3)法一:
不妨设 ,
因为S为规范数集,则 ,则 ,且 ,使得 ,
当 时,
则当 时,可得 ,
当且仅当 时,等号成立,
2
原创精品资源学科网独家享有版权,侵权必究!
0
学科网(北京)股份有限公司则范数 ,
当且仅当 时,等号成立,
又 ,
当且仅当 时,等号成立,
故 ,即范数 的最小值 ;
当 时,
则当 时,可得 ,
当且仅当 时,等号成立,则 ,
则范数 ,
当且仅当 时,等号成立,
又
,
当且仅当 时,等号成立,
故 ,即范数 的最小值 ;
当 ,使得 ,且 ,
当 ,即 ,即 时,
则当 时,可得 ,
当且仅当 时,等号成立,
则当 时,可得 ,
2
原创精品资源学科网独家享有版权,侵权必究!
1
学科网(北京)股份有限公司当且仅当 时,等号成立,
则范数
;
对于 ,其开口向上,对称轴为 ,
所以 ,
所以范数 的最小值为 ;
当 ,即 ,即 时,
则当 时,可得 ,
当且仅当 时,等号成立,
则当 时,可得 ,
当且仅当 时,等号成立,
则范数
2
原创精品资源学科网独家享有版权,侵权必究!
2
学科网(北京)股份有限公司;
对于 ,其开口向上,对称轴为 ,
所以 ,
所以范数 ;
综上所述:范数 的最小值 .
法二:不妨设 ,
因为S为规范数集,则 ,则 ,且 ,使得 ,
所以对于 ,同样有 ,则 ,
由(2)的证明过程与结论 可得, ,当且仅当
时,等号成立,
即 , ,…… ,
所以范数
,
当且仅当 时,等号成立,
所以范数 的最小值 .
2
原创精品资源学科网独家享有版权,侵权必究!
3
学科网(北京)股份有限公司