文档内容
2024年高考押题预测卷02【北京卷】
数学·全解全析
第一部分(选择题 共40分)
一、选择题:本题共10小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项是符合题目
要求的。
1 2 3 4 5 6 7 8 9 10
A D C D B A B B D C
1. 【答案】A
【分析】求 ,判断选项.
【详解】根据题意可得, ,
故选:A
2. 【答案】D
【分析】由 ,化简得到 求解.
【详解】解:因为复数 满足 ,
所以 ,
所以 的虚部为-3,
故选:D
3. 【答案】C
【分析】根据题意设出双曲线方程,在根据离心率公式,即可求出。
【详解】由题意知,双曲线的焦点在 轴上,
设双曲线的方程为 ,
因为双曲线C经过点 ,所以 ,
因为 ,所以 ,
所以 ,
所以双曲线的标准方程为 .
1
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司故选:C
4. 【答案】D
【分析】根据基本初等函数的单调性与奇偶性判断即可.
【详解】对于A: 定义域为 ,为非奇非偶函数,故A错误;
对于B: 定义域为 ,为奇函数,但是函数在 上单调递减,故B错误;
对于C: 为奇函数,定义域为 ,但是函数在 上不单调,故C错误;
对于D:令 定义域为 ,且 ,
所以 为奇函数,且当 时 ,函数在 上单调递增,故D正确.
故选:D
5.【答案】B
【分析】利用特殊值法,和对数函数的性质与逻辑关系进行判断选项.
【详解】若 ,由 ,取 ,但是 ,
而 ,则 ,又 ,则 中至少有一个大于1,
若都小于等于1,根据不等式的性质可知,乘积也小于等于1,与乘积大于1矛盾,
则 ,故 ,
所以 是 的必要而不充分条件.
故选:B
6.【答案】A
【分析】先利用余弦定理求出 ,再利用面积公式求解.
【详解】 ,
解得 ,则 ,
2
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司所以 .
故选:A.
7. 【答案】B
【分析】将 两边平方,即可得到 ,再由数量积的运算律计算可得.
【详解】因为 ,所以 ,
即 ,
所以 ,即 ,
所以 .
故选:B
8.【答案】B
【分析】根据给定条件,利用等差数列的性质求出 ,再求出 .
【详解】等差数列 中,由 ,得 ,解得 ,而 ,
所以 .
故选:B
9.【答案】D
【分析】
由直线方程得到其过定点 ,而 可看成单位圆上的一点,故可将求点 到直线之距转化
为求圆心到直线之距,要使距离最大,需使直线 ,此时最大距离即圆心到点 的距离再加上半
径即得.
【详解】由直线 整理得 ,可知直线经过定点 ,
而由 知,点 可看成圆 上的动点,
3
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司于是求点 到直线 的距离最值可通过求圆心到直线的距离得到.
如图知当直线 与圆相交时, 到直线 的距离最小值为 ,
要使点 到直线 距离最大,需使圆心 到直线 距离最大,
又因直线 过定点 ,故当且仅当 时距离最大,(若直线 与 不垂直,则过点 作直线 的垂
线段长必定比 短)
此时 ,故点 到直线 距离的最大值为 ,即 的最大值与最小值之差为
.
故选:D.
10.【答案】C
【分析】由已知可得 面 ,可得 上任意一点到平面 的距离相等,即可判断(1);点P
在直线 上运动时,直线 与平面 所成的角和直线 与平面 所成的角不相等,即可判断
(2);根据线面垂直的判定定理可证得 平面 ,再由线面垂直的性质即可判断(3);由线面
垂直的判定定理可证 平面 ,即可判断(4)
4
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司【详解】
对于(1),因为 , 面 , 面 ,所以 面 ,
所以 上任意一点到平面 的距离相等,又 ,所以三棱锥 的体积不变,故正
确;
对于(2),点P在直线 上运动时,直线AB与平面 所成的角和直线 与平面 所成的角不
相等,故错误;
对于(3),设 ,则 ,又 面 ,所以 ,又 ,所
以 平面 ,
又 平面 ,所以 ,所以点P在直线 上运动时,直线 与直线 所成的角的大
小不变,故正确;
对于(4),因为 为正方体,则 平面 ,且 平面 ,则 ,
又 ,且 , 平面 ,
所以 平面 ,且 平面 ,所以 ,
又 平面 ,且 平面 ,所以 ,又 ,
且 , 平面 ,所以 平面 ,
且 平面 ,所以 ,
5
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司又 , 平面 ,所以 平面 ,
且 平面 ,所以 ,故正确;
故选:C
第二部分(非选择题 共110分)
二、填空题:本题共5小题,每小题5分,共25分。
11.【答案】
【分析】根据题意,由题意可得二项式展开式的通项公式,代入计算,即可得到结果.
【详解】因为 展开式的通项公式为 ,
令 可得 ,则展开式中的常数项为 .
故答案为:
12.【答案】4
【分析】由抛物线的性质得到 到 的准线的距离,然后解出 的横坐标,最后求出 到直线 的
距离即可.
【详解】由点 在 上, 的焦点为 ,准线为 ,知 到直线 的距离等于 .
而 ,故 到直线 的距离为 .
设 的坐标为 ,由 到直线 的距离为 ,知 ,所以 或 .而 ,
故 .
所以 到直线 的距离为 .
故答案为: .
13. 【答案】 1
【分析】利用二倍角公式和辅助角公式,求解
6
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司【详解】 ,
由最大值为 , ,则 ,
所以 ,
所以 ,
故答案为: ;
14.【答案】 4 3或4
【分析】由已知利用等比数列的性质可求 ,又 ,可得 ,解得 或 ,
即可求得 ,分类讨论可求 的值,即可求解数列的各项,即可求解.
【详解】等比数列 中,公比 ;由 ,所以 ,又 ,
所以 解得 或 ;
若 时,可得 ,则 ,
且 的值为 ,可知数列 单调递增,且各项均大于 ,
所以不会存在 使得 的乘积最大(舍去);
若 时,可得 ,则 ,
且 的值为 ,…,
可知数列 单调递减,从第 项起各项小于 且为正数,
7
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司前 项均为正数且大于等于 ,
所以存在 或 ,使得 的乘积最大,
综上,可得 的一个可能值是3或 .
故答案为:4;3或4
15.【答案】②③
【分析】分析函数在 上的取值范围即可判断①,对零点在 、 讨论,即可判断②,③,
使得函数在各段单调性,且在断点左侧的函数值不大于断点右侧函数值,即可判断④.
【详解】因为 ,
当 时 ,则函数在 上单调递增,
又函数 的对称轴为 ,
对于①:当 时 ,
当 时 ,所以 ,即 ,故①错误;
对于②:当零点位于 时,则 ,解得 ,
此时 ,
若 ,即 时 在 上单调递增,
此时只需 ,解得 或 ,所以 ,
若 ,即 时,此时 ,则 在 上至少还有 个零点,故不符合题意,
所以 ;
8
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司当零点位于 ,此时 在 上无零点,则 ,解得 ,
此时 且 ,
要使函数 只有一个零点,则只需 ,解得 ,
又 ,显然 无解,所以此种情况不符合题意;
综上可得当 时 只有一个零点,故②正确;
对于③:使得 有三个不同零点,则必然是在 上有一个零点,在 上有两个零点,
则 ,解得 ,
所以当 时 有三个不同零点,故③正确;
对于④:若 在 上是单调递增函数,则 ,解得 ,
所以当 时 在 上是单调递增函数,故④错误.
故答案为:②③
【点睛】关键点点睛:第②问关键是分零点所在区间讨论,结合二次函数的性质得到不等式组,求出参数
的取值范围,第③问关键是分析得到在 上有一个零点,在 上有两个零点.
三、解答题:本题共6小题,共85分。解答应写出文字说明、证明过程或演算步棸。
16.(14分)【答案】(1)详见解析;(2)详见解析;(3) .
【分析】(1)由等腰三角形和直棱柱的性质,得出 和 ,根据线面垂直的判定定理,即
9
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司可证出 平面 ;
(2)连接 ,交 于点 ,连接 ,结合三角形的中位线得出 ,根据线面平行的判定定理,
即可证出 平面 ;
(3)连 ,交 于点 ,分别取 、 中点 、 ,连接 、 、 ,根据线面垂直的判定
定理,可证出 平面 和 平面 ,从而得出 就是二面角 的平面角,
最后利用几何法求出二面角 的余弦值.
【详解】解:(1)证明: , 是 中点, ,
又 在直三棱柱 中, 平面 , 平面 ,
,
又 , 平面 , 平面 ,
平面 .
(2)证明:连接 ,交 于点 ,连接 ,
、 分别是 、 的中点,
是 的中位线, ,
平面 , 平面 ,
平面
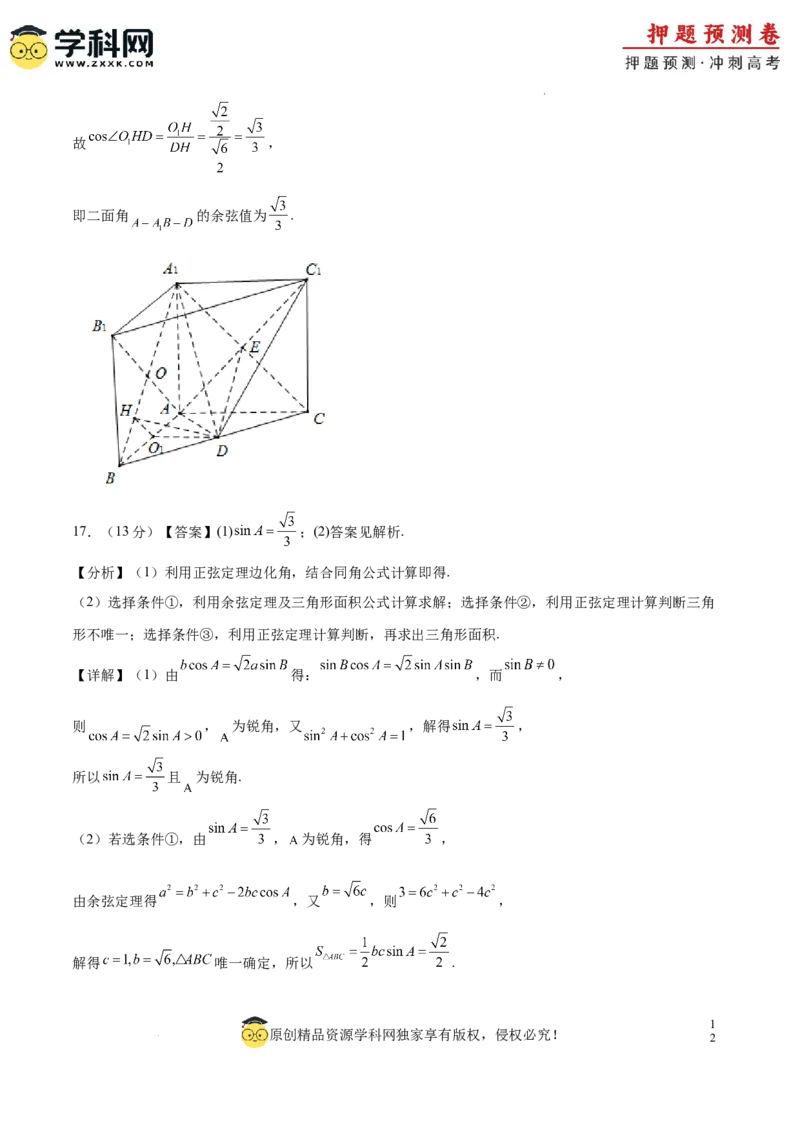
(3)解:连 ,交 于点 ,分别取 、 中点 、 ,连接 、 、 ,
四边形 是正方形且 、 分别是 、 的中点,故 ,
1
原创精品资源学科网独家享有版权,侵权必究!
0
学科网(北京)股份有限公司在 中, , ,
, ,
又 , 分别是 , 中点且 ,
,
又 在直三棱柱 中, 平面ABC, 平面ABC,
,
, 平面 , 平面 ,
平面 ,
平面 , 平面 ,
, ,
又 , , 平面 , 平面 ,
平面 ,
平面 , ,
又 平面 平面
就是二面角 的平面角,
设 ,则在 中, ,
,
故 ,
1
原创精品资源学科网独家享有版权,侵权必究!
1
学科网(北京)股份有限公司故 ,
即二面角 的余弦值为 .
17.(13分)【答案】(1) ;(2)答案见解析.
【分析】(1)利用正弦定理边化角,结合同角公式计算即得.
(2)选择条件①,利用余弦定理及三角形面积公式计算求解;选择条件②,利用正弦定理计算判断三角
形不唯一;选择条件③,利用正弦定理计算判断,再求出三角形面积.
【详解】(1)由 得: ,而 ,
则 , 为锐角,又 ,解得 ,
所以 且 为锐角.
(2)若选条件①,由 , 为锐角,得 ,
由余弦定理得 ,又 ,则 ,
解得 唯一确定,所以 .
1
原创精品资源学科网独家享有版权,侵权必究!
2
学科网(北京)股份有限公司若选条件②,由正弦定理得 ,则 ,
由 ,得 ,因此角 有两解,分别对应两个三角形,不符合题意.
若选条件③,由 , 为锐角,得 ,
又 ,得 , ,则 ,
因此 唯一确定,
由正弦定理得 ,则 ,所以 .
18.(13分)【答案】(1) , ;(2) ;(3)
【分析】(1)由题意得, ,从而求解 ,再结合表格数据与学生总人数求解 ;(2)先求解样
本符合题意的概率,然后由样本估计总体,得全市学生符合题意的概率,从而利用对立事件的概率公式求
解;(3)表示出参赛学生理论竞赛的平均成绩与方差,从而得关于 二次函数,由 的取值范围与二次函
数的性质从而求解得答案.
【详解】(1)由题意,理论或操作至少一项成绩为300分的学生
共有 人,则 ,
得 ,又 ,
得
(2)由(1)知,从20位理论成绩为300分的学生中抽取1人,
操作成绩也为300分的概率为 ,所以从全市理论成绩为300分的学生中,
随机抽取2人,至少有一个人操作的成绩为300分的概率为
(3)由题意, ,
1
原创精品资源学科网独家享有版权,侵权必究!
3
学科网(北京)股份有限公司设理论竞赛的分数为 ,则 取值为 ,
对应的人数分别为 ,所以参赛学生理论竞赛的平均成绩为
,
所以参赛学生理论成绩的方差为
因为 ,所以当 时, 最小.
19.(15分)【答案】(1) (2)
【分析】(1)根据椭圆的顶点坐标,结合斜率的计算公式,可整理椭圆方程,建立方程,可得答案;
(2)由题意,利用三角形中线性质,分割三角形,整理三角形面积表达式,联立直线与椭圆方程,写出
韦达定理,求得面积表达式中的变量,利用基本不等式,可得答案.
【详解】(1)由已知得 , 且 ,即 ,
因此有 ,得 .
因此 ,得 , ,所以椭圆的标准方程为 .
(2)显然直线 经过x轴上的定点 ,设 , ,
则由椭圆的对称性得 ,
联立 ,消去x得 .
恒成立,所以 , .
.
1
原创精品资源学科网独家享有版权,侵权必究!
4
学科网(北京)股份有限公司令 ,显然有 ,于是 ,当 ,即
时取等号.
因此 的面积S的最大值为 .
20.(15分) 【答案】(1) ; (2) .
【分析】(1)对 , 进行求导,已知在交点处有相同的切线,从而解出 的值及该切线的方程;
(2)由条件知 ,对 进行求导,分两种情况进行讨论:① ;② ,从而
求其最小值 的解析式;
【详解】(1)解: ,
由已知得 ,解得 ,
两条直线交点的坐标为 ,切线的斜率为 ,
切线的方程为 ,即切线的方程为 .
(2)解:由条件知
①当 时,令 ,解得 ,
当 时, 在 上递减;当 时, 在 上递增,
是 在 上的唯一极值点,从而也是 的最小值点,
最小值点, .
1
原创精品资源学科网独家享有版权,侵权必究!
5
学科网(北京)股份有限公司②当 时, 在 上递增,无最小值,故 的最小值 的解析式为
.
【点睛】本题主要考查导数的几何意义、利用导数研究函数的单调性从而求最值、分类讨论思想.属于难题.
分类讨论思想解决高中数学问题的一种重要思想方法,是中学数学四种重要的数学思想之一,尤其在解决
含参数问题发挥着奇特功效,大大提高了解题能力与速度.运用这种方法的关键是将题设条件研究透,这样
才能快速找准突破点. 充分利用分类讨论思想方法能够使问题条理清晰,进而顺利解答,希望同学们能够
熟练掌握并应用与解题当中.
21.(15分)【答案】(1) (2) (3)满足条件数列 的通项公式为: 或
,详见解析
【分析】(1)直接利用信息求出数列的项.
(2)利用恒成立问题和函数的单调性,求出λ的取值范围.
(3)直接利用分类讨论思想求出数列的通项公式.
【详解】(1)数列 为“Γ数列”中, ,
所以:当 时, 时, ,
又 ,即: ,
, .
(2)因为数列 是“Γ数列”,且 ,所以:
,
则:数列前4n项中的项bn 是以2为首项,6为公差的等差数列.
4 -3
易知{bn}的项后按原来的顺序构成一个首项为4,公差为2的等差数列.
4
所以:
1
原创精品资源学科网独家享有版权,侵权必究!
6
学科网(北京)股份有限公司,
.
由于不等式 对 恒成立,
所以: ,
设 ,
则: ,
所以:
当 时, ,
当 时, ,
所以:
所以 的最大值为 .
即 .
(3) 为等比数列,设数列 的公比 ,
由等比数列的通项公式: ,
当 时, ,
即: ,
① ,则 ,故: .
②当 时,则: ,
所以 为常数,则 ,k为偶数时,
1
原创精品资源学科网独家享有版权,侵权必究!
7
学科网(北京)股份有限公司经检验,满足条件数列 的通项公式为: 或 .
1
原创精品资源学科网独家享有版权,侵权必究!
8
学科网(北京)股份有限公司