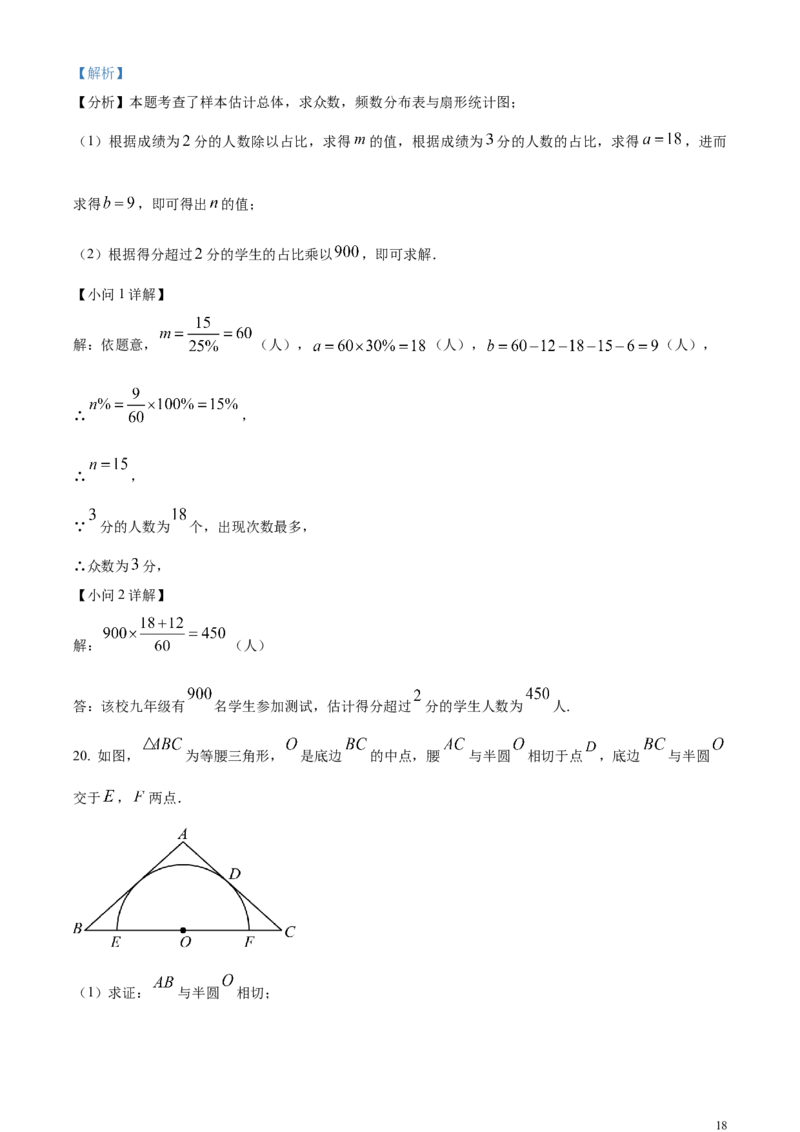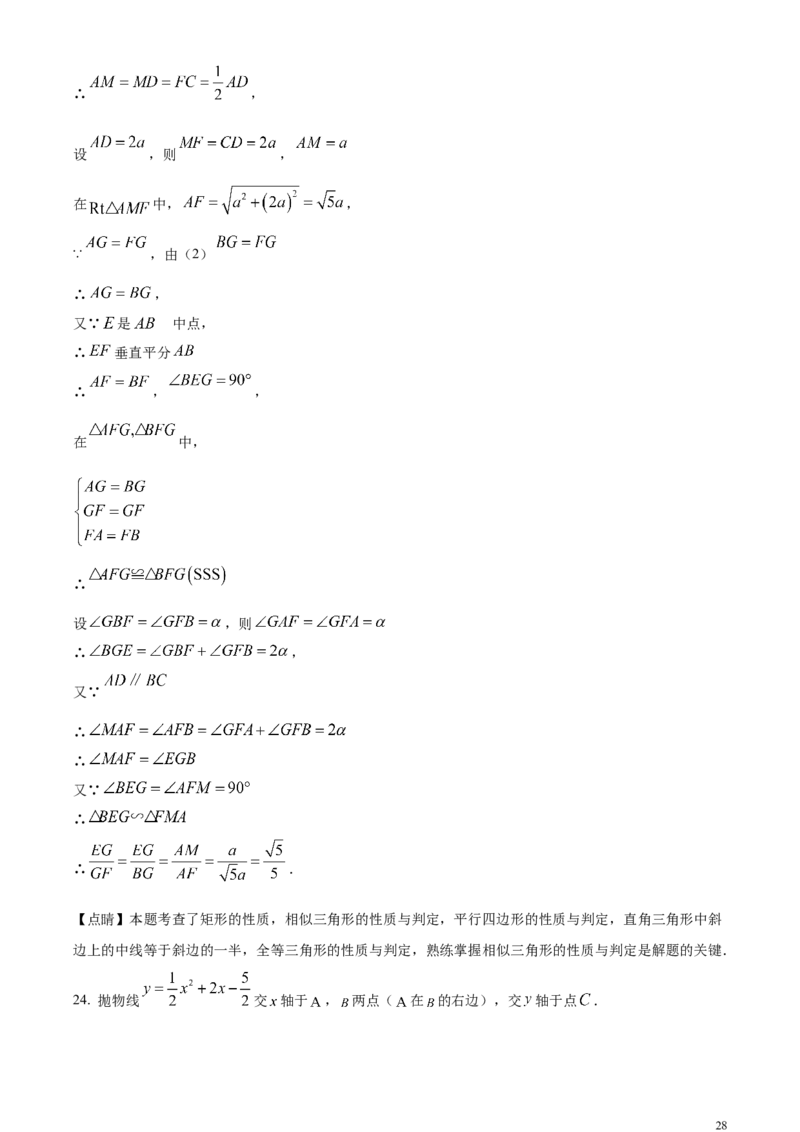文档内容
2024 年武汉市初中毕业生学业考试
数学试卷
亲爱的同学:
在你答题前,请认真阅读下面的注意事项:
1.本试卷全卷共6页,三大题,满分120分.考试用时120分钟.
2.答题前,请将你的姓名、准考证号填写在“答题卡”相应位置,并在“答题卡”背面左上
角填写姓名和座位号.
3.答选择题时,选出每小题答案后,用2B铅笔将“答题卡”上对应题目的答案标号涂黑.
如需改动,用橡皮擦干净后,再选涂其他答案.答在“试卷”上无效.
4.答非选择题时,答案用0.5毫米黑色笔迹签字笔书写在“答题卡”上.答在“试卷”上无
效.
5.认真阅读答题卡上的注意事项.
预祝你取得优异成绩!
一、选择题(共10小题,每小题3分,共30分)
下列各题中有且只有一个正确答案,请在答题卡上将正确答案的标号涂黑.
1. 现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列汉字是轴对称图形的是(
)
A. B. C. D.
【答案】C
【解析】
【分析】本题考查了轴对称图形的识别,根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重
合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
【详解】解:A,B,D选项中的图形不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分
能够互相重合,所以不是轴对称图形,
C选项中的图形能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是
轴对称图形.
故选:C.
2. 小美和小好同学做“石头、剪刀、布”的游戏,两人同时出相同的手势,这个事件是( )
1A. 随机事件 B. 不可能事件 C. 必然事件 D. 确定性事件
【答案】A
【解析】
【分析】本题考查 的是必然事件、不可能事件、随机事件的概念.根据事件发生的可能性大小判断即可.
【详解】解:两人同时出相同的手势,,这个事件是随机事件,
故选:A.
3. 如图是由两个宽度相同的长方体组成的几何体,它的主视图是( )
A. B. C. D.
【答案】B
【解析】
【分析】本题考查了三视图的知识,熟知主视图是从物体的正面看到的视图是解题的关键.按照主视图的
定义逐项判断即可.
【详解】解:从正面看该几何体,下面是一个大长方形,上面叠着一个小长方形,
故选:B.
4. 国家统计局2024年4月16日发布数据,今年第一季度国内生产总值接近 亿元,同比增长 ,
国家高质量发展取得新成效.将数据 用科学记数法表示是( )
A. B. C. D.
【答案】C
【解析】
【分析】本题考查了科学记数法.科学记数法的表示形式为 的形式,其中 , 为整
数.确定 的值时,要看把原数变成 时,小数点移动了多少位, 的绝对值大于 与小数点移动的位数相
同.
【详解】解: ,
2故选:C.
5. 下列计算正确的是( )
A. B. C. D.
【答案】B
【解析】
【分析】本题考查了完全平方公式,积的乘方,幂的乘方,同底数幂的乘法等,根据同底数幂的乘法,积
的乘方,幂的乘方,完全平方公式运算法则分别判断即可.
【详解】解:A. ,故该选项不正确,不符合题意;
B. ,故该选项正确,符合题意;
C. ,故该选项不正确,不符合题意;
D. ,故该选项不正确,不符合题意;
故选:B.
6. 如图,一个圆柱体水槽底部叠放两个底面半径不等的实心圆柱体,向水槽匀速注水.下列图象能大致反
映水槽中水的深度h与注水时间t的函数关系的是( )
A. B. C. D.
【答案】D
【解析】
【分析】本题考查了函数图象;根据题意,分3段分析,即可求解.
【详解】解:下层圆柱底面半径大,水面上升块,上层圆柱底面半径稍小,水面上升稍慢,再往上则水面
上升更慢,
所以对应图象是第一段比较陡,第二段比第一段缓,第三段比第二段缓.
故选:D.
37. 小美同学按如下步骤作四边形 :①画 ;②以点 为圆心, 个单位长为半径画弧,分
别交 , 于点 , ;③分别以点 , 为圆心, 个单位长为半径画弧,两弧交于点 ;④连接
, , .若 ,则 的大小是( )
A. B. C. D.
【答案】C
【解析】
【分析】本题考查了基本作图,菱形的判定和性质,根据作图可得四边形 是菱形,进而根据菱形
的性质,即可求解.
【详解】解:作图可得
∴四边形 是菱形,
∴
∵ ,
∴ ,
∴ ,
故选:C.
8. 经过某十字路口的汽车,可能直行,也可能向左转或向右转,这三种可能性大小相同.若两辆汽车经过
这个十字路口,则至少一辆车向右转的概率是( )
A. B. C. D.
【答案】D
4【解析】
【分析】本题考查的是运用树状图求概率,运用树状图法确定所有情况数和符合题意情况数是解答本题的
关键.
运用树状图法确定所有情况数和符合题意情况数,然后用概率公式解答即可.
【详解】解:列树状图如图所示,
共有9种情况,至少一辆车向右转有5种,
∴至少一辆车向右转的概率是 ,
故选:D.
9. 如图,四边形 内接于 , , , ,则
的半径是( )
A. B. C. D.
【答案】A
【解析】
【分析】延长 至点E,使 ,连接 ,连接 并延长交 于点F,连接 ,即可证得
,进而可求得 ,再利用圆周角定理得到 ,
结合三角函数即可求解.
5【详解】解:延长 至点E,使 ,连接 ,连接 并延长交 于点F,连接 ,
∵四边形 内接于 ,
∴
∴
∵
∴ ,
∴ 是 的直径,
∴
∴ 是等腰直角三角形,
∴
∵
∴
∴ , ,
∵
∴
又∵
∴
∴ 是等腰直角三角形
6∴
∵
∴
∵
∴
∴
故选:A.
【点睛】本题考查了全等三角形的性质与判定,圆周角定理,锐角三角函数、等腰三角形的性质与判定等
知识点,熟练掌握圆周角定理以及全等三角形的性质与判定是解题的关键.
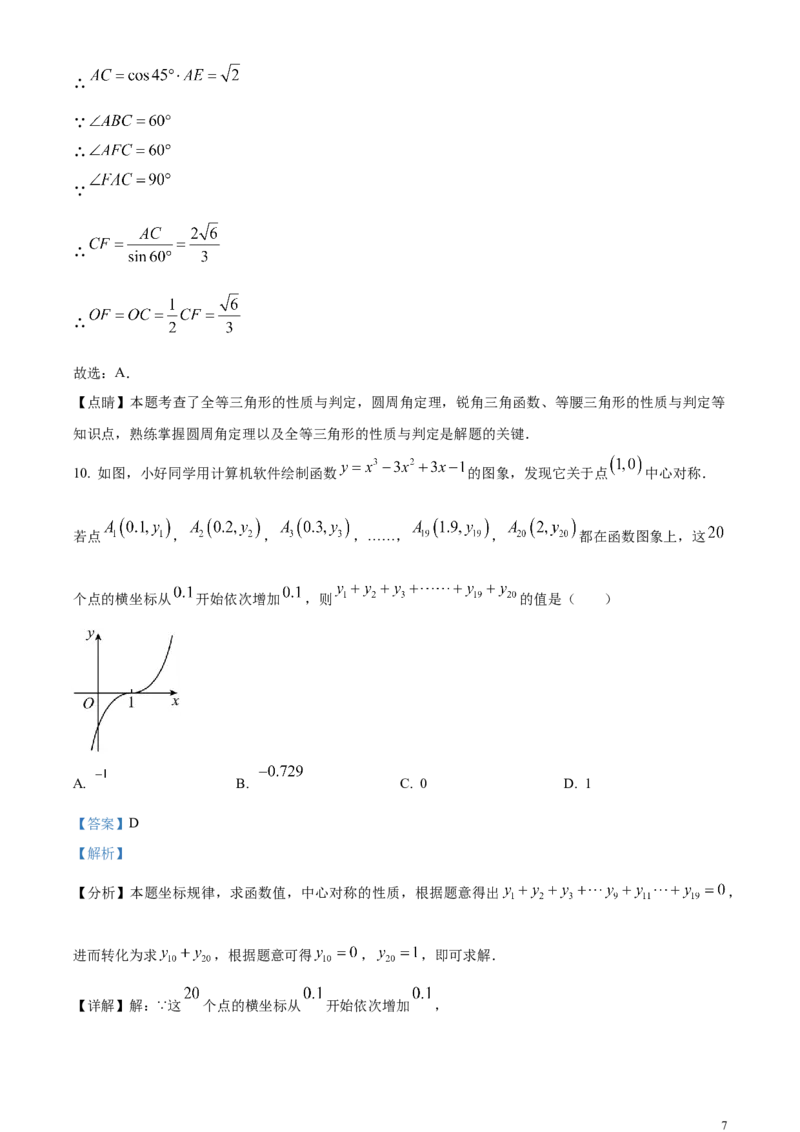
10. 如图,小好同学用计算机软件绘制函数 的图象,发现它关于点 中心对称.
若点 , , ,……, , 都在函数图象上,这
个点的横坐标从 开始依次增加 ,则 的值是( )
A. B. C. 0 D. 1
【答案】D
【解析】
【分析】本题坐标规律,求函数值,中心对称的性质,根据题意得出 ,
进而转化为求 ,根据题意可得 , ,即可求解.
【详解】解:∵这 个点的横坐标从 开始依次增加 ,
7∴ ,
∴ ,
∴ ,而 即 ,
∵ ,
当 时, ,即 ,
∵ 关于点 中心对称的点为 ,
即当 时, ,
∴ ,
故选:D.
二、填空题(共6小题,每小题3分,共18分)
下列各题不需要写出解答过程,请将结果直接填写在答题卡指定的位置.
11. 中国是世界上最早使用负数的国家.负数广泛应用到生产和生活中,例如,若零上 记作 ,则
零下 记作_________ .
【答案】
【解析】
【分析】本题考查了正数和负数的意义,在一对具有相反意义的量中,先规定其中一个为正,则另一个就
用负表示.
【详解】解:零上 记作 ,则零下 记作 .,
故答案为: .
12. 某反比例函数 具有下列性质:当 时,y随x的增大而减小,写出一个满足条件的k的值是
__________.
【答案】1(答案不唯一)
【解析】
【分析】本题考查的是反比例函数的性质,反比例函数的图象是双曲线,当 ,双曲线的两支分别位
8于第一、第三象限,在每一象限内y随x的增大而减小,当 ,双曲线的两支分别位于第二、第四象限,
在每一象限内y随x的增大而增大.直接根据反比例函数的性质写出符合条件的的值即可.
【详解】解:∵当 时,y随x的增大而减小,
∴
故答案为:1(答案不唯一).
13. 分式方程 的解是______.
【答案】
【解析】
【分析】本题主要考查了解分式方程,熟练掌握解分式方程的方法和步骤是解题关键.首先等号两边同时
乘以 完成去分母,再按照去括号,移项、合并同类项的步骤求解,检验即可获得答案.
【详解】解: ,
等号两边同时乘以 ,得 ,
去括号,得 ,
移项、合并同类项,得 ,
经检验, 是该分式方程的解,
所以,该分式方程的解为 .
故答案为: .
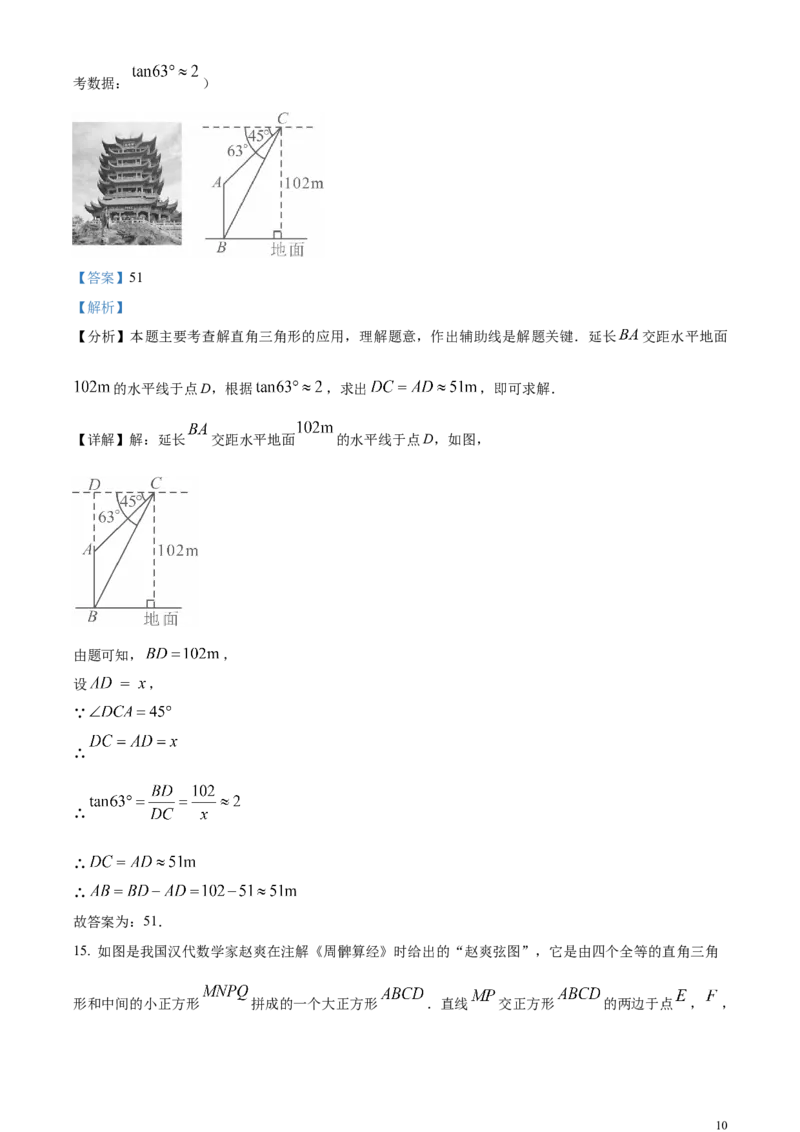
14. 黄鹤楼是武汉市著名的旅游景点,享有“天下江山第一楼”的美誉.在一次综合实践活动中,某数学
小组用无人机测量黄鹤楼 的高度,具体过程如下:如图,将无人机垂直上升至距水平地面 的C
处,测得黄鹤楼顶端A的俯角为 ,底端B的俯角为 ,则测得黄鹤楼的高度是__________m.(参
9考数据: )
【答案】51
【解析】
【分析】本题主要考查解直角三角形的应用,理解题意,作出辅助线是解题关键.延长 交距水平地面
的水平线于点D,根据 ,求出 ,即可求解.
【详解】解:延长 交距水平地面 的水平线于点D,如图,
由题可知, ,
设 ,
∵
∴
∴
∴
∴
故答案为:51.
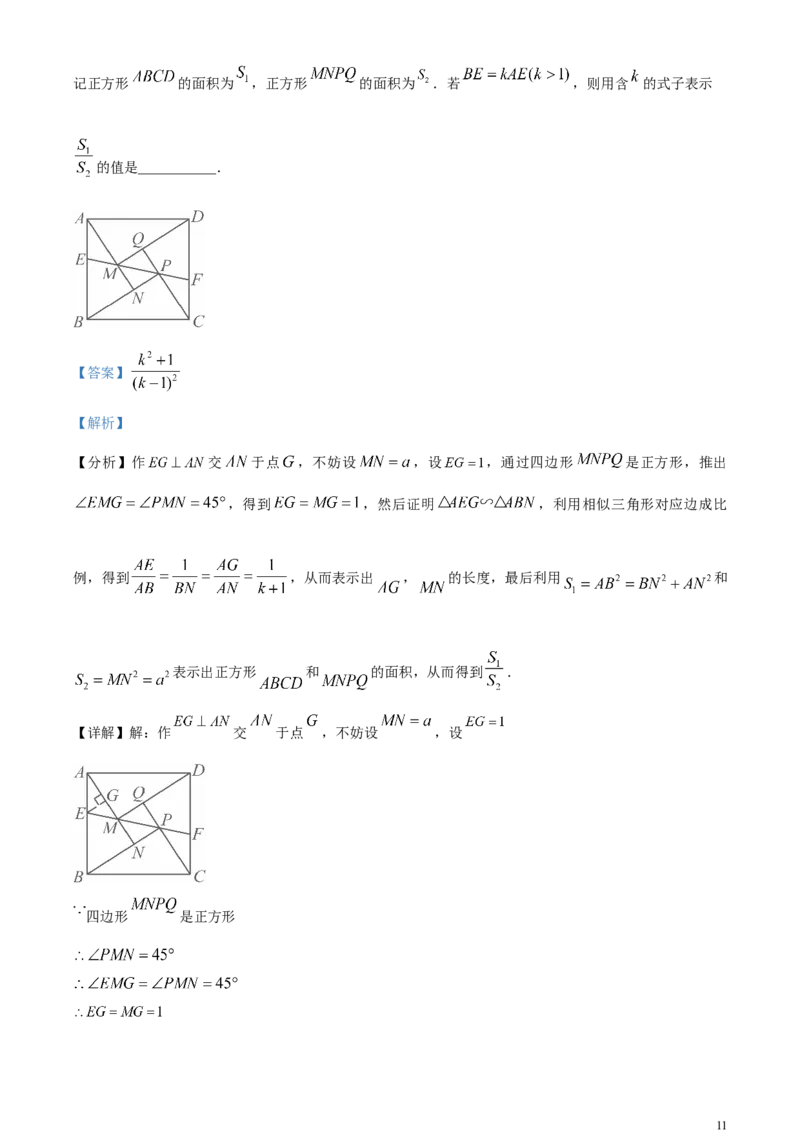
15. 如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,它是由四个全等的直角三角
形和中间的小正方形 拼成的一个大正方形 .直线 交正方形 的两边于点 , ,
10记正方形 的面积为 ,正方形 的面积为 .若 ,则用含 的式子表示
的值是___________.
【答案】
【解析】
【分析】作 交 于点 ,不妨设 ,设 ,通过四边形 是正方形,推出
,得到 ,然后证明 ,利用相似三角形对应边成比
例,得到 ,从而表示出 , 的长度,最后利用 和
表示出正方形 和 的面积,从而得到 .
【详解】解:作 交 于点 ,不妨设 ,设
四边形 是正方形
11在 和 中, ,
由题意可知,
正方形 的面积 ,
正方形 的面积
【点睛】本题考查了弦图,正方形的性质,等角三角形的性质,相似三角形的判定与性质,正方形的面积,
勾股定理,熟练掌握以上知识点并能画出合适的辅助线构造相似三角形是解题的关键.
1216. 抛物线 (a,b,c是常数, )经过 , 两点,且 .下列四个
结论:
① ;
②若 ,则 ;
③若 ,则关于x的一元二次方程 无实数解;
④点 , 在抛物线上,若 , ,总有 ,则 .
其中正确的是__________(填写序号).
【答案】②③④
【解析】
【分析】本题考查了二次函数的性质,根据题意可得抛物线对称轴 ,即可判断①,根据
, 两点之间的距离大于 ,即可判断②,根据抛物线经过 得出 ,代入顶点纵
坐标,求得纵坐标的最大值即可判断③,根据④可得抛物线的对称轴 ,解不等式,即
可求解.
【详解】解:∵ (a,b,c是常数, )经过 , 两点,且 .
∴对称轴为直线 , ,
∵ ,
∴ ,故①错误,
∵
∴ ,即 , 两点之间 的距离大于
13又∵
∴ 时,
∴若 ,则 ,故②正确;
③由①可得 ,
∴ ,即 ,
当 时,抛物线解析式为
设顶点纵坐标为
∵抛物线 (a,b,c是常数, )经过 ,
∴
∴
∴
∵ , ,对称轴为直线 ,
∴当 时, 取得最大值为 ,而 ,
∴关于x的一元二次方程 无解,故③正确;
④∵ ,抛物线开口向下,点 , 在抛物线上, , ,总有
,
14又 ,
∴点 离 较远,
∴对称轴
解得: ,故④正确.
故答案为:②③④.
三、解答题(共8小题,共72分)
下列各题需要在答题卡指定的位置写出文字说明、证明过程、演算步骤或画出图形.
17. 求不等式组 的整数解.
【答案】整数解为:
【解析】
【分析】本题考查了解一元一次不等式组,分别求出每一个不等式的解集,根据口诀:同大取大、同小取
小、大小小大中间找、大大小小找不到确定不等式组的解集,进而求得整数解.
【详解】解:
解不等式①得:
解不等式②得:
的
∴不等式组 解集为: ,
为
∴整数解 :
18. 如图,在 中,点 , 分别在边 , 上, .
15(1)求证: ;
(2)连接 .请添加一个与线段相关的条件,使四边形 是平行四边形.(不需要说明理由)
【答案】(1)见解析 (2)添加 (答案不唯一)
【解析】
【分析】本题考查了平行四边形的性质与判定,全等三角形的判定;
(1)根据平行四边形的性质得出 , ,结合已知条件可得 ,即可证明
;
(2)添加 ,依据一组对边平行且相等的四边形是平行四边形,即可求解.
【小问1详解】
证明:∵四边形 是平行四边形,
∴ , , ,
∵ ,
∴ 即 ,
在 与 中,
,
∴ ;
【小问2详解】
添加 (答案不唯一)
如图所示,连接 .
16∵四边形 是平行四边形,
∴ ,即 ,
当 时,四边形 是平行四边形.
19. 为加强体育锻炼,增强学生体质,某校在“阳光体育一小时”活动中组织九年级学生定点投篮技能测
试,每人投篮 次,投中一次计 分.随机抽取 名学生的成绩作为样本,将收集的数据整理并绘制成如
下的统计图表.
测试成绩频数分布表
成 频
绩/分 数
根据以上信息,解答下列问题:
(1)直接写出 , 的值和样本的众数;
(2)若该校九年级有 名学生参加测试,估计得分超过 分的学生人数.
【答案】(1) , ,众数为 分
(2)该校九年级有 名学生参加测试,估计得分超过 分的学生人数为 人
17【解析】
【分析】本题考查了样本估计总体,求众数,频数分布表与扇形统计图;
(1)根据成绩为 分的人数除以占比,求得 的值,根据成绩为 分的人数的占比,求得 ,进而
求得 ,即可得出 的值;
(2)根据得分超过 分的学生的占比乘以 ,即可求解.
【小问1详解】
解:依题意, (人), (人), (人),
∴ ,
∴ ,
∵ 分的人数为 个,出现次数最多,
∴众数为 分,
【小问2详解】
解: (人)
答:该校九年级有 名学生参加测试,估计得分超过 分的学生人数为 人.
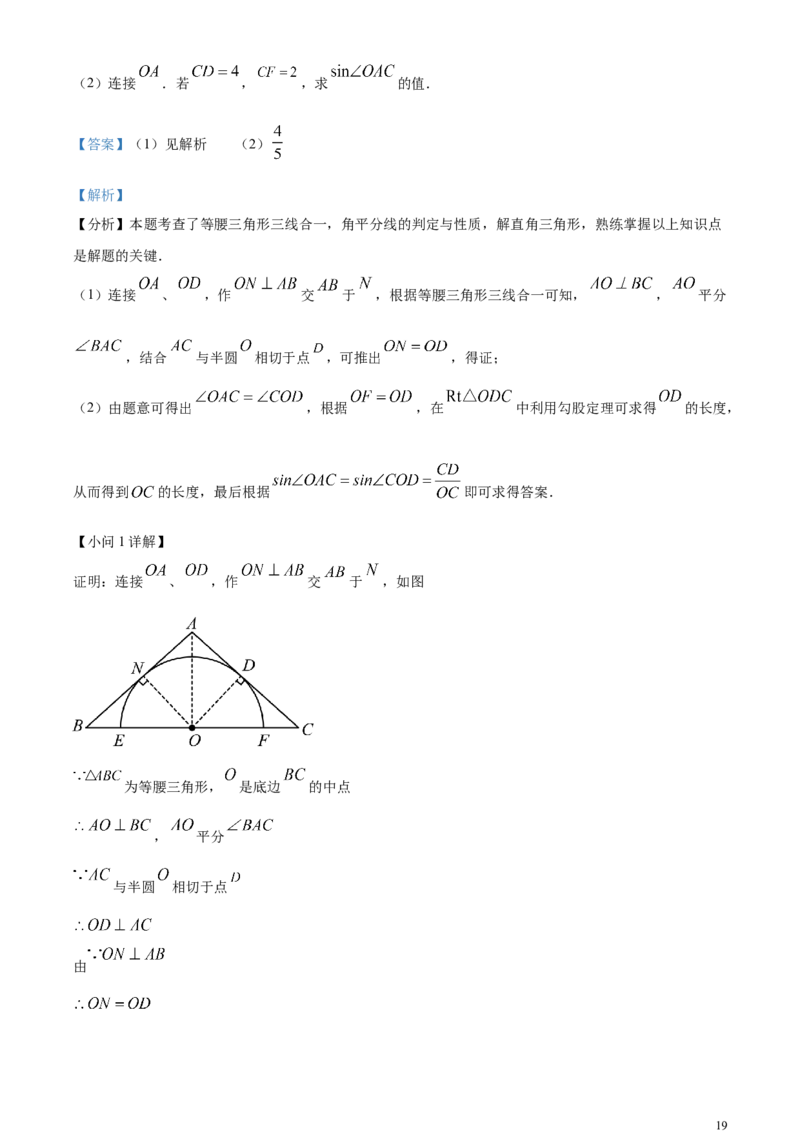
20. 如图, 为等腰三角形, 是底边 的中点,腰 与半圆 相切于点 ,底边 与半圆
交于 , 两点.
(1)求证: 与半圆 相切;
18(2)连接 .若 , ,求 的值.
【答案】(1)见解析 (2)
【解析】
【分析】本题考查了等腰三角形三线合一,角平分线的判定与性质,解直角三角形,熟练掌握以上知识点
是解题的关键.
(1)连接 、 ,作 交 于 ,根据等腰三角形三线合一可知, , 平分
,结合 与半圆 相切于点 ,可推出 ,得证;
(2)由题意可得出 ,根据 ,在 中利用勾股定理可求得 的长度,
从而得到 的长度,最后根据 即可求得答案.
【小问1详解】
证明:连接 、 ,作 交 于 ,如图
为等腰三角形, 是底边 的中点
, 平分
与半圆 相切于点
由
19是半圆 的切线
【小问2详解】
解:由(1)可知 ,
,
,
又 ,
在 中, ,
,
解得:
21. 如图是由小正方形组成的 网格,每个小正方形的顶点叫做格点. 三个顶点都是格点.仅用
无刻度的直尺在给定网格中完成四个画图任务,每个任务的画线不得超过三条.
(1)在图(1)中,画射线 交 于点D,使 平分 的面积;
(2)在(1)的基础上,在射线 上画点E,使 ;
(3)在图(2)中,先画点F,使点A绕点F顺时针旋转 到点C,再画射线 交 于点G;
20(4)在(3)的基础上,将线段 绕点G旋转 ,画对应线段 (点A与点M对应,点B与点N
对应).
【答案】(1)作图见解析
(2)作图见解析 (3)作图见解析
(4)作图见解析
【解析】
【分析】本题考查了网格作图.熟练掌握全等三角形性质,平行四边形性质,等腰三角形性质,等腰直角
三角形性质,是解题的关键.
(1)作矩形 ,对角线 交 于点D,做射线 ,即可;
(2)作 ,射线 于点Q,连接 交 于点E,即可;
(3)在 下方取点F,使 , 是等腰直角三角形,连接 , , 交
于点G,即可;
(4)作 ,交 于点M,作 ,交 于点N,连接 ,即可.
【小问1详解】
如图,作线段 ,使四边形 是矩形, 交 于点D,做射线 ,点D即为所求作;
【小问2详解】
如图,作 ,作 于点Q,连接 交 于点E,点E即为作求作;
21【小问3详解】
如图,在 下方取点F,使 ,连接 ,连接并延长 , 交 于点G,点F,
G即为所求作;
【小问4详解】
如图,作 ,交射线 于点M,作 ,交 于点N,连接 ,线段 即为所求作.
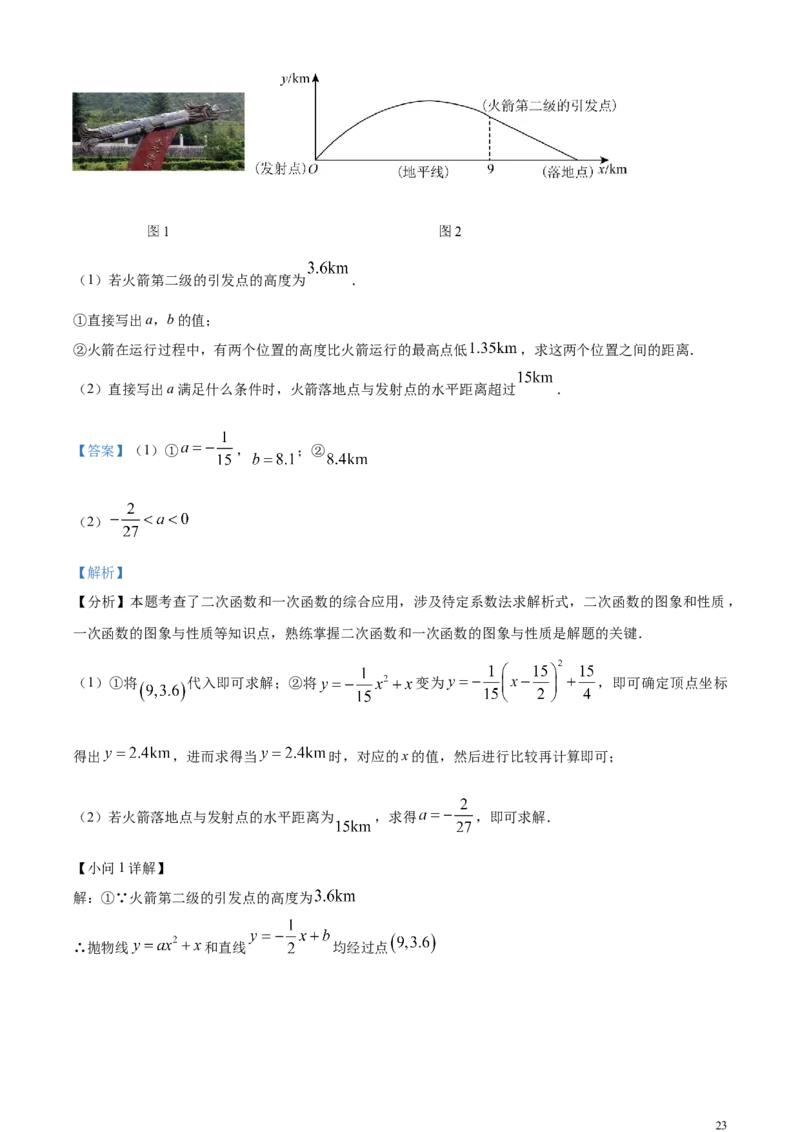
22. 16世纪中叶,我国发明了一种新式火箭“火龙出水”,它是二级火箭的始祖.火箭第一级运行路径形
如抛物线,当火箭运行一定水平距离时,自动引发火箭第二级,火箭第二级沿直线运行.某科技小组运用
信息技术模拟火箭运行过程.如图,以发射点为原点,地平线为x轴,垂直于地面的直线为y轴,建立平
面直角坐标系,分别得到抛物线 和直线 .其中,当火箭运行的水平距离为
时,自动引发火箭的第二级.
22(1)若火箭第二级的引发点的高度为 .
①直接写出a,b的值;
②火箭在运行过程中,有两个位置的高度比火箭运行的最高点低 ,求这两个位置之间的距离.
(2)直接写出a满足什么条件时,火箭落地点与发射点的水平距离超过 .
【答案】(1)① , ;②
(2)
【解析】
【分析】本题考查了二次函数和一次函数的综合应用,涉及待定系数法求解析式,二次函数的图象和性质,
一次函数的图象与性质等知识点,熟练掌握二次函数和一次函数的图象与性质是解题的关键.
(1)①将 代入即可求解;②将 变为 ,即可确定顶点坐标
得出 ,进而求得当 时,对应的x的值,然后进行比较再计算即可;
(2)若火箭落地点与发射点的水平距离为 ,求得 ,即可求解.
【小问1详解】
解:①∵火箭第二级的引发点的高度为
∴抛物线 和直线 均经过点
23∴ ,
解得 , .
②由①知, ,
∴
∴最大值
当 时,
则
解得 ,
又∵ 时,
∴当 时,
则
解得
∴这两个位置之间的距离 .
【小问2详解】
解:当水平距离超过 时,
24火箭第二级的引发点为 ,
将 , 代入 ,得
,
解得 ,
∴ .
23. 问题背景:如图(1),在矩形 中,点 , 分别是 , 的中点,连接 , ,求
证: .
问题探究:如图(2),在四边形 中, , ,点 是 的中点,点 在边
上, , 与 交于点 ,求证: .
问题拓展:如图(3),在“问题探究”的条件下,连接 , , ,直接写出 的
值.
【答案】问题背景:见解析;问题探究:见解析;问题拓展:
【解析】
【分析】问题背景:根据矩形的性质可得 ,根据点 , 分别是 ,
25的中点,可得 ,即可得证;
问题探究:取 的中点 ,连接 ,得 是 的中位线,根据已知条件可得 平行且
等于 ,进而可得 是平行四边形,得 ,则 ,根据直角三角形中斜边
上的中线等于斜边的一半得出 ,进而可得 ,等量代换可得 ,
等角对等边,即可得证;
问题拓展:过点 作 ,则四边形 是矩形,连接 ,根据已知以及勾股定理得出
;根据(2)的结论结合已知可得 ,证明 垂直平分 ,进而得出
,证明 ,进而证明 , 进而根据相似三角形的性质,即可求解.
【详解】问题背景:∵四边形 是矩形,
∴ ,
∵ , 分别是 , 的中点
∴ ,
即 ,
∴ ;
问题探究:如图所示,取 的中点 ,连接 ,
26∵ 是 的中点, 是 的中点,
∴ ,
又∵ ,
∴ ,
∵ ,
∴
∴四边形 是平行四边形,
∴
∴
又∵ , 是 的中点,
∴
∴
∴ ,
∴ ;
问题拓展:如图所示,过点 作 ,则四边形 是矩形,连接 ,
∵ ,
27∴ ,
设 ,则 ,
在 中, ,
∵ ,由(2)
∴ ,
又∵ 是 中的点,
∴ 垂直平分
∴ , ,
在 中,
∴
设 ,则
∴ ,
又∵
∴
∴
又∵
∴
∴ .
【点睛】本题考查了矩形的性质,相似三角形的性质与判定,平行四边形的性质与判定,直角三角形中斜
边上的中线等于斜边的一半,全等三角形的性质与判定,熟练掌握相似三角形的性质与判定是解题的关键.
24. 抛物线 交 轴于 , 两点( 在 的右边),交 轴于点 .
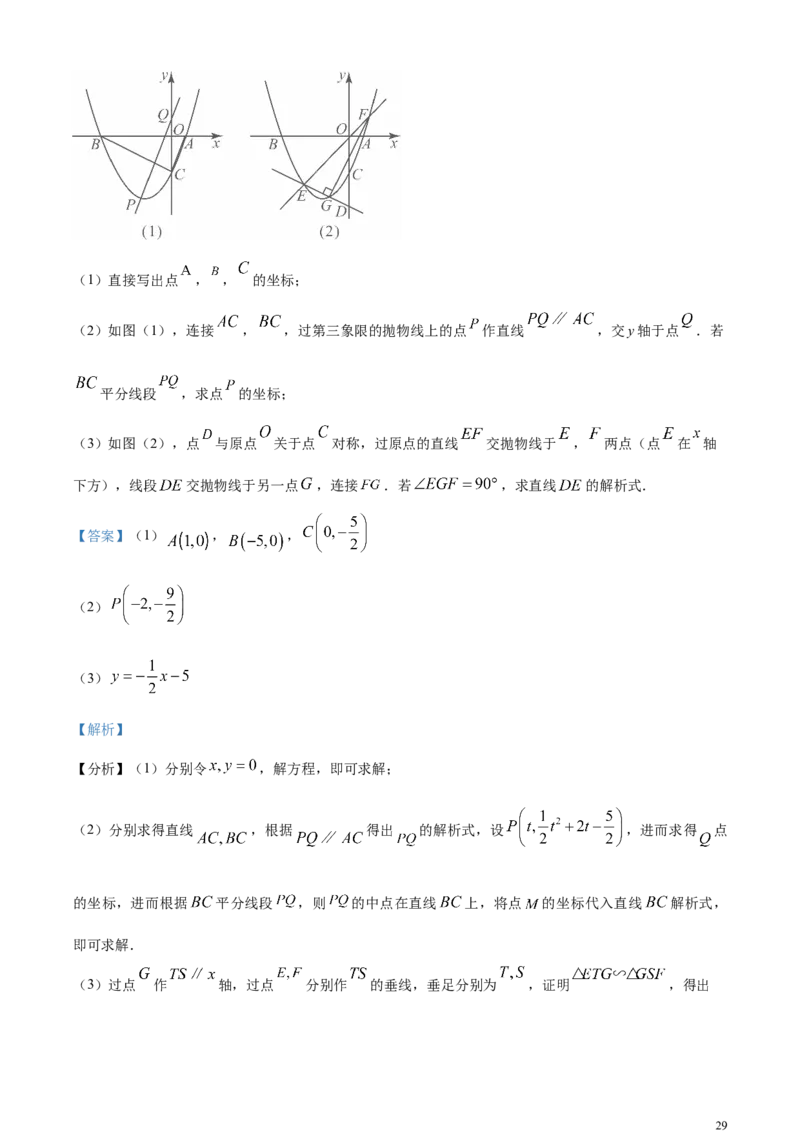
28(1)直接写出点 , , 的坐标;
(2)如图(1),连接 , ,过第三象限的抛物线上的点 作直线 ,交y轴于点 .若
平分线段 ,求点 的坐标;
(3)如图(2),点 与原点 关于点 对称,过原点的直线 交抛物线于 , 两点(点 在 轴
下方),线段 交抛物线于另一点 ,连接 .若 ,求直线 的解析式.
【答案】(1) , ,
(2)
(3)
【解析】
【分析】(1)分别令 ,解方程,即可求解;
(2)分别求得直线 ,根据 得出 的解析式,设 ,进而求得 点
的坐标,进而根据 平分线段 ,则 的中点在直线 上,将点 的坐标代入直线 解析式,
即可求解.
(3)过点 作 轴,过点 分别作 的垂线,垂足分别为 ,证明 ,得出
29,先求得点 的坐标,设直线 的解析式为 ,直线 的解析式为
,联立抛物线解析式,设 , , 根据一元二次方程根与系数的关系,得
出 , , ,进而求得 ,代入 ,化简后得出
,即 ,进而即可求解.
【小问1详解】
解:由 ,
当 时, ,则
当 ,
解得:
∵ 在 的右边
∴ , ,
【小问2详解】
解:设直线 的解析式为
将 , 代入得,
解得:
30∴直线 的解析式为
∵
设直线 的解析式为
∵ 在第三象限的抛物线上
设 ,
∴
∴
∴
设 的中点为 ,则
由 , ,设直线 的解析式为 ,
将 代入得,
,
解得:
∴直线 的解析式为 ,
∵ 平分线段 ,
31∴ 在直线 上,
∴
解得: (舍去)
当 时,
∴ ;
【小问3详解】
解:如图所示,过点 作 轴,过点 分别作 的垂线,垂足分别为 ,
∴
∴
∴
∴
即
∵点 与原点 关于点 对称,
∴ ,
设直线 的解析式为 ,直线 的解析式为
32联立直线 与抛物线解析式 可得, ,
即
联立直线 与抛物线解析式 可得,
即
设 , ,
∴ , , ,
∴
,
∵
∴ ,
将 代入得:
∴ ,
∴ ,
∴直线 解析式为 .
33【点睛】本题考查了二次函数综合问题,一次函数与二次函数综合,中点坐标公式,相似三角形的性质与
判定,一元二次方程根与系数的关系,熟练掌握以上知识是解题的关键.
34