文档内容
2013年普通高等学校招生全国统一考试(江苏卷)
参考公式:
1 n 1 n
样本数据x ,x , ,x 的方差s2 = å(x -x)2 ,其中x = åx 。
1 2 L n n i n i
i=1 i=1
1
棱锥的体积公式:V = Sh,其中S是锥体的底面积,h为高。
3
棱柱的体积公式:V =Sh,其中S是柱体的底面积,h为高。
一、填空题:本大题共14小题,每小题5分,共计70分,请把答案填写在答题卡的相应位
置上。
p
1、函数y =3sin(2x+ )的最小正周期为 ▲ 。
4
2、设z =(2-i)2 (i为虚数单位),则复数z的模为 ▲ 。
x2 y2
3、双曲线 - =1的两条渐近线的方程为 ▲ 。
16 9
4、集合{-1,0,1}共有 ▲ 个子集。
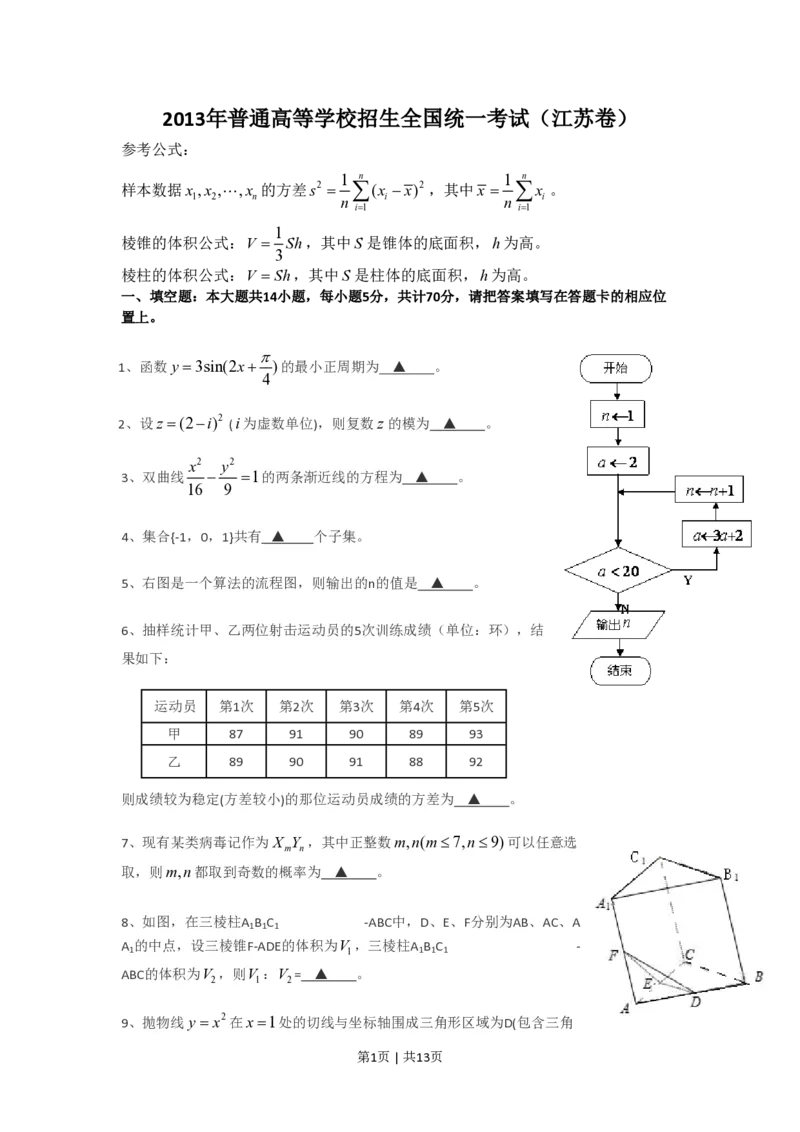
5、右图是一个算法的流程图,则输出的n的值是 ▲ 。
6、抽样统计甲、乙两位射击运动员的5次训练成绩(单位:环),结
果如下:
运动员 第1次 第2次 第3次 第4次 第5次
甲 87 91 90 89 93
乙 89 90 91 88 92
则成绩较为稳定(方差较小)的那位运动员成绩的方差为 ▲ 。
7、现有某类病毒记作为X Y ,其中正整数m,n(m£7,n£9)可以任意选
m n
取,则m,n都取到奇数的概率为 ▲ 。
8、如图,在三棱柱A B C -ABC中,D、E、F分别为AB、AC、A
1 1 1
A 的中点,设三棱锥F-ADE的体积为V ,三棱柱A B C -
1 1 1 1 1
ABC的体积为V ,则V :V = ▲ 。
2 1 2
9、抛物线y = x2在x=1处的切线与坐标轴围成三角形区域为D(包含三角
第1页 | 共13页形内部与边界)。若点P(x,y)是区域D内的任意一点,则x+2y的取值范围是 ▲ 。
1 2
10、设D、E分别是△ABC的边AB、BC上的点,且AD= AB,BE = BC。若
2 3
uuur uuur uuur
DE =lAB+lAC (l、l均为实数),则l+l的值为 ▲ 。
1 2 1 2 1 2
11、已知 f(x)是定义在R上的奇函数。当x>0时, f(x)= x2 -4x,则不等式 f(x)> x
的解集用区间表示为 ▲ 。
x2 y2
12、在平面直角坐标系xoy中,椭圆C的方程为 + =1(a>b>0),右焦点为F,右准
a2 b2
线为l,短轴的一个端点为B。设原点到直线BF的距离为d ,F到l的距离为d 。若
1 2
d = 6d ,则椭圆C的离心率为 ▲ 。
2 1
1
13、在平面直角坐标系xoy中,设定点A(a,a),P是函数y = (x>0)图象上的一动点。若点
x
P、A之间的最短距离为2 2,则满足条件的实数a的所有值为= ▲ 。
14、在正项等比数列a 中,
n
1
a
5
=
2
,a
6
+a
7
=3,则满足a
1
+a
2
+
L
+a
n
>a
1
a
2L
a
n
的最大正整数n的值为 ▲
。
二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说
明、证明或演算步骤.
15、(本小题满分14分)
r r
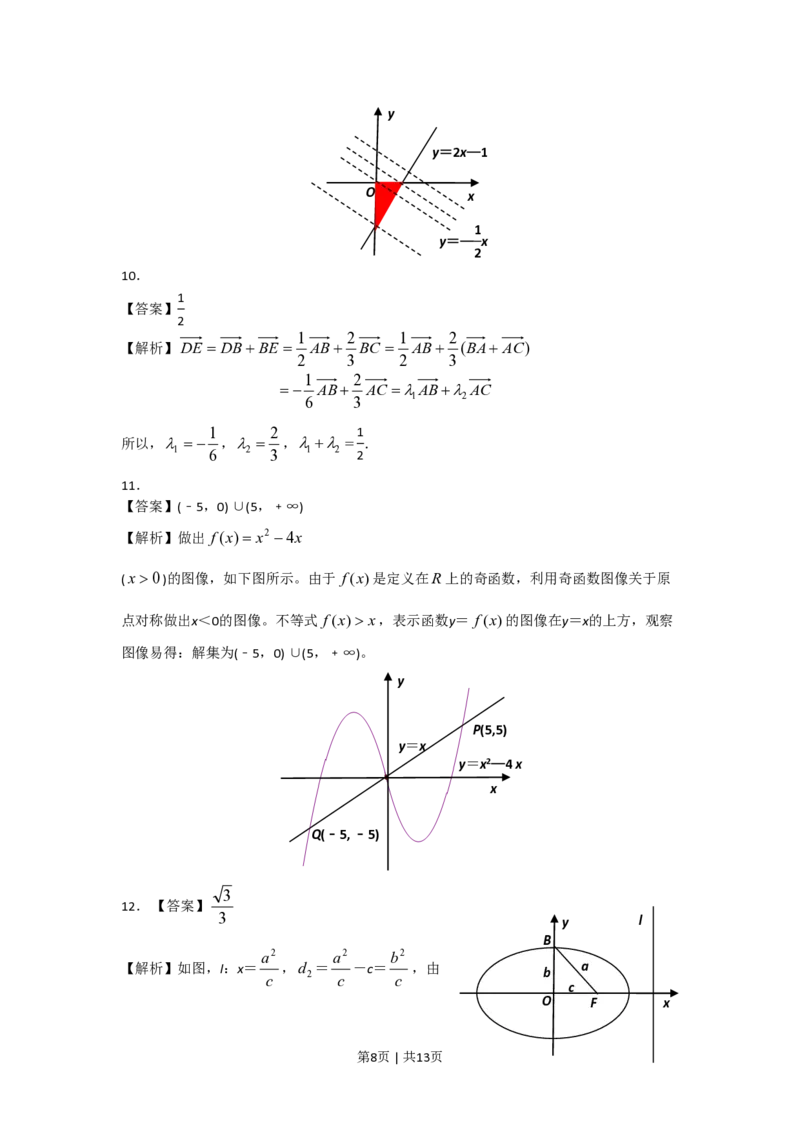
已知向量a=(cosa,sina),b=(cosb,sinb),00)的图像,如下图所示。由于 f(x)是定义在R上的奇函数,利用奇函数图像关于原
点对称做出x<0的图像。不等式 f(x)> x,表示函数y= f(x)的图像在y=x的上方,观察
图像易得:解集为(﹣5,0) ∪(5,﹢∞)。
y
P(5,5)
y=x
y=x2—4 x
x
Q(﹣5, ﹣5)
3
12. 【答案】
3 y l
B
a2 a2 b2
【解析】如图,l:x=
c
,d
2
=
c
-c=
c
,由
b
a
c
O F x
第8页 | 共13页bc b2 bc
等面积得:d = 。若d = 6d ,则 = 6 ,整理得: 6a2 -ab- 6b2 =0
1 a 2 1 c a
2
b b b 6
,两边同除以:a2,得: 6 - + 6 =0,解之得: = ,所以,离心率
a a a 3
2
b 3
为:e = 1- = .
a 3
13.
【答案】1或 10
【解析】
14.
【答案】12
ì 1
a q = 1
【解析】设正项等比数列{a n }首项为a 1 ,公比为q,则:í 1 4 2 ,得:a 1 =
32
a q (1+q) =3
î
1 5
2n -1 (n-1)n
,q=2,a
n
=26-n.记T
n
= a
1
+a
2
+
L
+a
n
=
25
,
n
= a
1
a
2L
a
n
= 2 2 .
2n -1 (n-1)n 1 n2- 11 n+5 1 11
T > ,则 > 2 2 ,化简得:2n -1> 22 2 ,当n > n2 - n+5时,
n n 25 2 2
13+ 121
n = 12.当n=12时,T > ,当n=13时,T < ,故n =12.
2 12 12 13 13 max
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文
字说明、证明过程或演算步骤.
15.
解:(1)a-b=(cosα-cosβ,sinα-sinβ),
|a-b|2=(cosα-cosβ)2+(sinα-sinβ)2=2-2(cosα·cosβ+sinα·sinβ)=2,
所以,cosα·cosβ+sinα·sinβ=0,
所以,a ^b.
ìcosa+cosb=0 ① 1
(2)í ,①2+②2得:cos(α-β)=- .
îsina+sinb=1 ② 2
2 2
所以,α-β= p,α= p+β,
3 3
第9页 | 共13页2 3 1 p
带入②得:sin( p+β)+sinβ= cosβ+ sinβ=sin( +β)=1,
3 2 2 3
p p
所以, +β= .
3 2
5p p
所以,α= ,β= .
6 6
16.
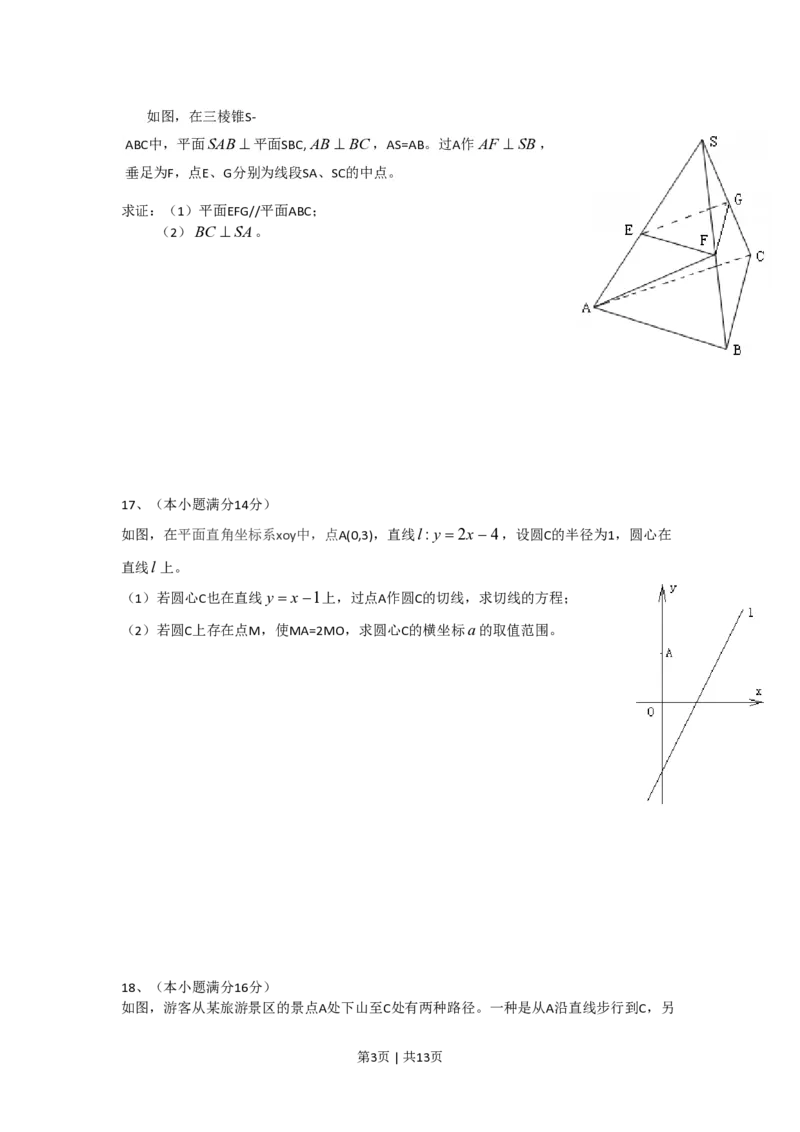
证:(1)因为SA=AB且AF⊥SB, S
所以F为SB的中点.
E G
又E,G分别为SA,SC的中点,
F
所以,EF∥AB,EG∥AC.
C
又AB∩AC=A,AB面SBC,AC面ABC, A
所以,平面EFG//平面ABC.
(2)因为平面SAB⊥平面SBC,平面SAB∩平面SBC=BC,
B
AF平面ASB,AF⊥SB.
所以,AF⊥平面SBC.
又BC平面SBC,
所以,AF⊥BC.
又AB⊥BC,AF∩AB=A,
所以,BC⊥平面SAB.
又SA平面SAB,
所以,BC ^ SA.
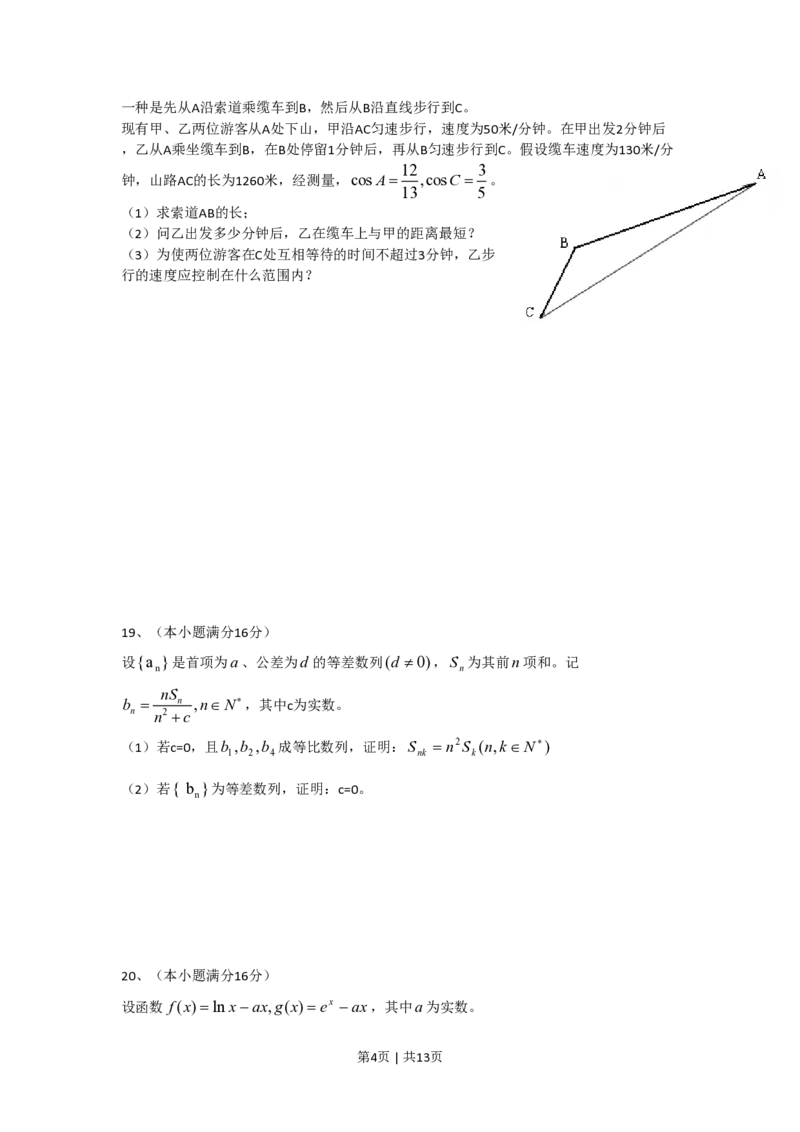
ì y = x-1
17. 解:(1)联立:í ,得圆心为:C(3,2).
îy = 2x-4
y
设切线为:y = kx+3,
l
A
|3k +3-2| 3
d= = r =1,得:k =0 or k = - .
1+k2 4 O x
3
故所求切线为:y =0 or y = - x+3.
4
(2)设点M(x,y),由MA=2MO,知: x2 +(y-3)2 = 2 x2 + y2 ,
化简得:x2 +(y+1)2 = 4,
即:点M的轨迹为以(0,1)为圆心,2为半径的圆,可记为圆D.
又因为点M 在圆C上,故圆C圆D的关系为相交或相切.
故:1≤|CD|≤3,其中 CD = a2 +(2a-3)2 .
12
解之得:0≤a≤ .
5
A
18.
M
B
N
第10页 | 共13页
D
C解:(1)如图作BD⊥CA于点D,
设BD=20k,则DC=25k,AD=48k,
AB=52k,由AC=63k=1260m,
知:AB=52k=1040m.
(2)设乙出发x分钟后到达点M,
此时甲到达N点,如图所示.
则:AM=130x,AN=50(x+2),
由余弦定理得:MN2=AM2+AN2-2 AM·ANcosA=7400 x2-14000 x+10000,
35
其中0≤x≤8,当x= (min)时,MN最小,此时乙在缆车上与甲的距离最短.
37
1260 126
(3)由(1)知:BC=500m,甲到C用时: = (min).
50 5
126 141 86
若甲等乙3分钟,则乙到C用时: +3= (min),在BC上用时: (min) .
5 5 5
86 1250
此时乙的速度最小,且为:500÷ = m/min.
5 43
126 111 56
若乙等甲3分钟,则乙到C用时: -3= (min),在BC上用时: (min) .
5 5 5
56 625
此时乙的速度最大,且为:500÷ = m/min.
5 14
1250 625
故乙步行的速度应控制在[ , ]范围内.
43 14
19.
n[(n-1)d +2a] (n-1)d +2a
证:(1)若c =0,则a = a+(n-1)d ,S = ,b = .
n n 2 n 2
当b,b,b 成等比数列,b2 =bb ,
1 2 4 2 1 4
2
d 3d
即:a+ = aa+ ,得:d2 = 2ad,又d 0,故d =2a.
2 2
由此:S = n2a,S =(nk)2a = n2k2a,n2S = n2k2a.
n nk k
故:S =n2S (k,nÎN*).
nk k
(n-1)d +2a
n2
nS
2
(2)b = n = ,
n n2 +c n2 +c
(n-1)d +2a (n-1)d +2a (n-1)d +2a
n2 +c -c
2 2 2
=
n2 +c
(n-1)d +2a
c
(n-1)d +2a 2
= - . (※)
2 n2 +c
若{b }是等差数列,则b = An+Bn型.
n n
第11页 | 共13页观察(※)式后一项,分子幂低于分母幂,
(n-1)d +2a
c
2 (n-1)d +2a (n-1)d +2a
故有: =0,即c =0,而 ≠0,
n2 +c 2 2
故c =0.
经检验,当c =0时{b }是等差数列.
n
20.
1 1
解:(1) f (x) = -a≤0在(1,+)上恒成立,则a≥ , x Î (1,+).
x x
故:a≥1.
g(x) =ex -a,
若1≤a≤e,则g(x) =ex -a≥0在(1,+)上恒成立,
此时,g(x)=ex -ax在(1,+)上是单调增函数,无最小值,不合;
若a>e,则g(x)=ex -ax在(1,lna)上是单调减函数,在(lna,+)上是单
调增函数,g (x) = g(lna),满足.
min
故a的取值范围为:a>e.
(2)g(x) =ex -a≥0在(-1,+)上恒成立,则a≤ex,
1
故:a≤ .
e
1 1-ax
f (x) = -a = (x >0).
x x
1 1
(ⅰ)若0<a≤ ,令 f (x)>0得增区间为(0, );
e a
1
令 f (x)<0得减区间为( ,﹢∞).
a
当x→0时,f(x)→﹣∞;当x→﹢∞时,f(x)→﹣∞;
1 1 1
当x= 时,f( )=﹣lna-1≥0,当且仅当a= 时取等号.
a a e
1 1
故:当a= 时,f(x)有1个零点;当0<a< 时,f(x)有2个零点.
e e
(ⅱ)若a=0,则f(x)=﹣lnx,易得f(x)有1个零点.
1
(ⅲ)若a<0,则 f (x) = -a > 0在(0,+)上恒成立,
x
即: f(x)=lnx-ax在(0,+)上是单调增函数,
当x→0时,f(x)→﹣∞;当x→﹢∞时,f(x)→﹢∞.
此时,f(x)有1个零点.
第12页 | 共13页1 1
综上所述:当a= 或a<0时,f(x)有1个零点;当0<a< 时,f(x)有2个零点.
e e
第13页 | 共13页