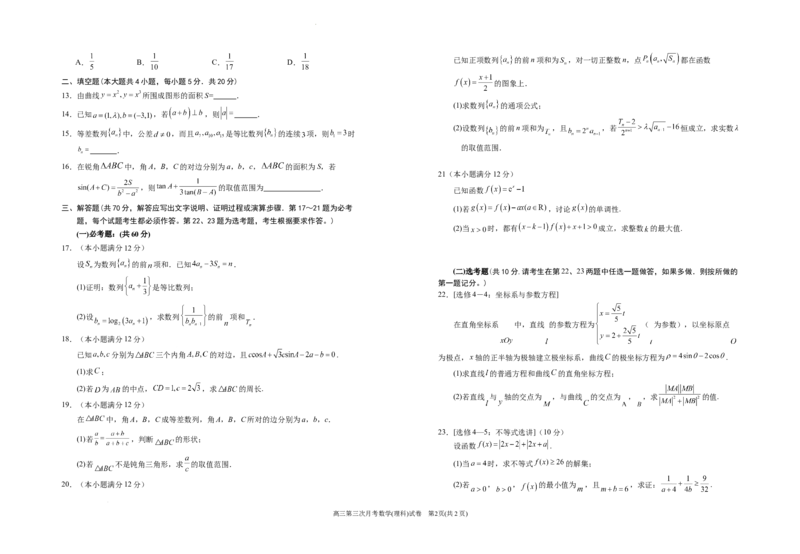文档内容
银川一中2024届高三年级第三次月考
C. D.
理 科 数 学
7.函数 是定义在 上的偶函数,且 在区间 上单调递增,若关于实数
命题教师:张金荣
t
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。 的不等式 恒成立,则 的取值范围是
2.作答时,务必将答案写在答题卡上。写在本试卷及草稿纸上无效。
3.考试结束后,将本试卷和答题卡一并交回。
A. B. C. D.
一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只
有一项是符合题目要求的)
8.函数 的图象大致为
1.已知集合 , ,则
A. B. C. D.
2.使不等式 成立的一个充分不必要条件是 A. B. C. D.
A. B. C. D.
3.已知复数z满足 ,则
A. B. C. D.
4.已知 , , ,则
9.化简 的值为
A. B. C. D.
A.1 B. C. D.2
5.为了保障交通安全,某地根据《道路交通安全法》规定:汽车驾驶员血液中的酒精含量
不得超过0.09mg/mL.据仪器监测,某驾驶员喝了二两白酒后,血液中的酒精含量迅速 10.已知数列 , 中满足 , , ,若 前 项之
上
和为 ,则满足不等式 的最小整数 是
升到0.3mg/mL,在停止喝酒后,血液中每小时末的酒精含量都比上一个小时末减少
25%, A.8 B.9 C.11 D.10
那么此人在开车前至少要休息(参考数据: , )
11.已知在 中,角 的对边分别为 , ,点Q在边BC上,且满足
A.4.1小时 B.4.2小时 C.4.3小时 D.4.4小时
( ), ,则 的最小值是
6.已知函数 的部分图像
A.32 B.64 C.100 D.120
如图所示,则 解析式为
12.设函数 ,若关于 的不等式 有解,则实数
A. B.
的值为
高三第三次月考数学(理科)试卷 第1页(共2页)
学科网(北京)股份有限公司已知正项数列 的前n项和为 ,对一切正整数n,点 都在函数
A. B. C. D.
二、填空题(本大题共4小题,每小题5分.共20分) 的图象上.
13.由曲线 所围成图形的面积S= .
(1)求数列 的通项公式;
14.已知 ,若 ,则 .
(2)设数列 的前n项和为 ,且 ,若 恒成立,求实数λ
15.等差数列 中,公差 ,而且 是等比数列 的连续 项,则 时
的取值范围.
.
16.在锐角 中,角A,B,C的对边分别为a,b,c, 的面积为S,若
21(本小题满分12分)
,则 的取值范围为 .
已知函数
三、解答题(共70分,解答应写出文字说明、证明过程或演算步骤.第17~21题为必考 (1)若 ,讨论 的单调性.
题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。)
(2)当 时,都有 成立,求整数 的最大值.
(一)必考题:(共60分)
17.(本小题满分12分)
设 为数列 的前 项和.已知 .
(二)选考题(共10分.请考生在第22、23两题中任选一题做答,如果多做.则按所做的
第一题记分。)
(1)证明:数列 是等比数列;
22.[选修4-4:坐标系与参数方程]
(2)设 ,求数列 的前 项和 .
在直角坐标系 中,直线 的参数方程为 ( 为参数),以坐标原点
18.(本小题满分12分)
已知 分别为 三个内角 的对边,且 .
为极点, 轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为 .
(1)求 ; (1)求直线 的普通方程和曲线 的直角坐标方程;
(2)若 为 的中点, ,求 的周长.
(2)若直线 与 轴的交点为 ,与曲线 的交点为 , ,求 的值.
19.(本小题满分12分)
在 中,角A,B,C成等差数列,角A,B,C所对的边分别为a,b,c.
23.[选修4—5:不等式选讲](10分)
(1)若 ,判断 的形状;
设函数 .
(2)若 不是钝角三角形,求 的取值范围. (1)当 时,求不等式 的解集;
20.(本小题满分12分) (2)若 , , 的最小值为 ,且 ,求证: .
高三第三次月考数学(理科)试卷 第2页(共2页)
学科网(北京)股份有限公司高三第三次月考数学(理科)试卷 第3页(共2页)
学科网(北京)股份有限公司