文档内容
银川一中2024 届高三年级第二次月考
8.等比数列 的前 项和为 ,已知 ,且 与 的等差中项为 ,则
文 科 数 学 A.29 B.31 C.33 D.36
9.意大利画家列奥纳多·达·芬奇的画作《抱银鼠的女子》(如图所示)中,
命题教师:李伟 女士颈部的黑色珍珠项链与她怀中的白貂形成对比.光线和阴影衬托出
人物的优雅和柔美.达·芬奇提出:固定项链的两端,使其在重力的作用
注意事项:
下自然下垂,形成的曲线是什么?这就是著名的“悬链线问题”.后人研
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.作答时,务必将答案写在答题卡上。写在本试卷及草稿纸上无效。 究得出,悬链线并不是抛物线,而是与解析式为 的“双曲余
3.考试结束后,将本试卷和答题卡一并交回。
弦函数”相关.下列选项为“双曲余弦函数”图象的是
一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只
有一项是符合题目要求的)
1.已知集合 , ,则 的子集个数为 A. B. C. D.
A.2 B.4 C.3 D.8
2.已知 ,则在复平面内,复数 对应的点位于
A.第三象限 B.第四象限 C.第一象限 D.第二象限 10.设 为等差数列 的前 项和,且 ,都有 .若 ,则
3.下列命题正确的是
A. 的最小值是 B. 的最小值是
A.命题“若 ,则 ”的否命题为“若 ,则 ”
C. 的最大值是 D. 的最大值是
B.若给定命题 , ,则 ,
C.已知 , ,则 是 的充分必要条件 11.已知函数 的图象如图
D.若 为假命题,则 ,q都为假命题
所示,图象与 轴的交点为 ,与 轴的交点为 ,最高
4.若函数 在点 处的切线方程为 ,则实数 的值为
A. B. C. D. 点 ,且满足 .若将 的图象向左平移1个
5.已知 , 为钝角, ,则 单位得到的图象对应的函数为 ,则
α
A.1 B. C.2 D.
A. B.0 C. D.
6.已知 , , ,则 , , 的大小关系为 12.高斯是德国著名的数学家,近代数学的奠基者之一,享有“数学王子”的称号,用其名
字命名的“高斯函数”为:设 ,用 表示不超过x的最大整数,则 称为
A. B. C. D.
“高斯函数”,例如: , .已知数列 满足 , ,
7.已知向量 , ,且 ,则 与 夹角为
,若 , 为数列 的前n项和,则
A. B. C. D.
学科网(北京)股份有限公司 高三第二次月考数学(文科)试卷 第1页(共2页)
学科网(北京)股份有限公司 司(1)求 的通项公式;
A. B. C. D.
(2)若 ,求数列 的前 项和 .
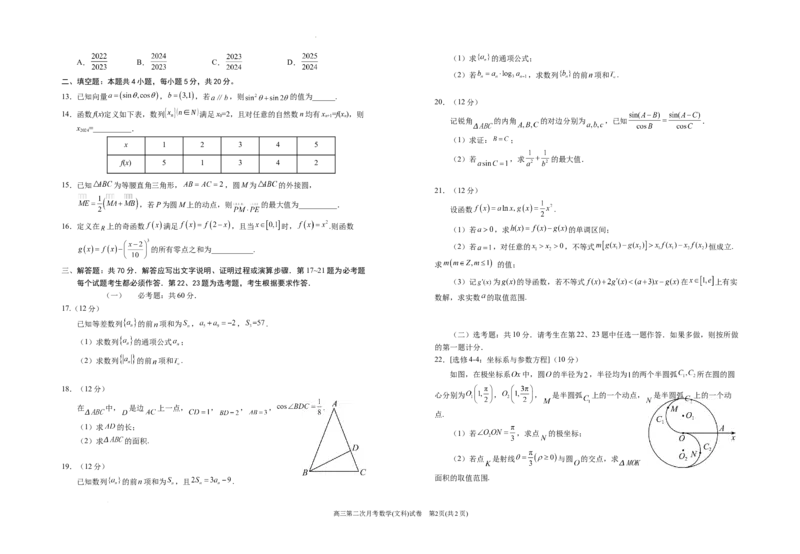
二、填空题:本题共4小题,每小题5分,共20分。
13.已知向量 , ,若 ,则 的值为______.
20.(12分)
14.函数f(x)定义如下表,数列{x }(n∈N)满足x=2,且对任意的自然数n均有x =f(x),则
n 0 n+1 n
记锐角 的内角 的对边分别为 ,已知 .
ΔABC
x =__________.
2024
(1)求证: ;
x 1 2 3 4 5
(2)若 ,求 的最大值.
f(x) 5 1 3 4 2
15.已知 为等腰直角三角形, ,圆M为 的外接圆,
21.(12分)
,若P为圆M上的动点,则 的最大值为__________.
设函数 .
16.定义在 上的奇函数 满足 ,且当 时, .则函数
(1)若 ,求 的单调区间;
(2)若 ,对任意的 ,不等式 恒成立.
的所有零点之和为___________.
求 的值;
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题
每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (3)记 为 的导函数,若不等式 在 上有实
(一) 必考题:共60分. 数解,求实数 的取值范围.
17.(12分)
已知等差数列 的前 项和为 , , .
(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做
(1)求数列 的通项公式 ;
的第一题计分.
(2)求数列 的前 项和 . 22.[选修4-4:坐标系与参数方程](10分)
如图,在极坐标系 中,圆 的半径为 ,半径均为 的两个半圆弧 所在圆的圆
18.(12分)
心分别为 , , 是半圆弧 上的一个动点, 是半圆弧 上的一个动
在 中, 是边 上一点, , , , .
ΔABC
点.
(1)求 的长;
(1)若 ,求点 的极坐标;
(2)求ΔABC的面积.
(2)若点 是射线 与圆 的交点,求
ΔMOK
19.(12分)
面积的取值范围.
已知数列 的前 项和为 ,且 .
学科网(北京)股份有限公司 高三第二次月考数学(文科)试卷 第2页(共2页)
学科网(北京)股份有限公司 司23.[选修4-5:不等式选讲](10分)
已知 ,求证:
(1) ;
(2) .
学科网(北京)股份有限公司 高三第二次月考数学(文科)试卷 第3页(共2页)
学科网(北京)股份有限公司 司