文档内容
2024届新高三开学摸底考试卷(新高考专用)01
数学•全解全析
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一
项是符合题目要求的。
1.设集合 ,B= ,则 ( )
A. {-2,-1,1} B. {-2, 0, 1}
C. {-2,-1} D. {-1, 1}
【答案】A
【详解】 ,则 或 ,
所以 .
故选:A.
2.已知复数 , 为z的共轭复数,则 ( )
A. B. 2 C. D.
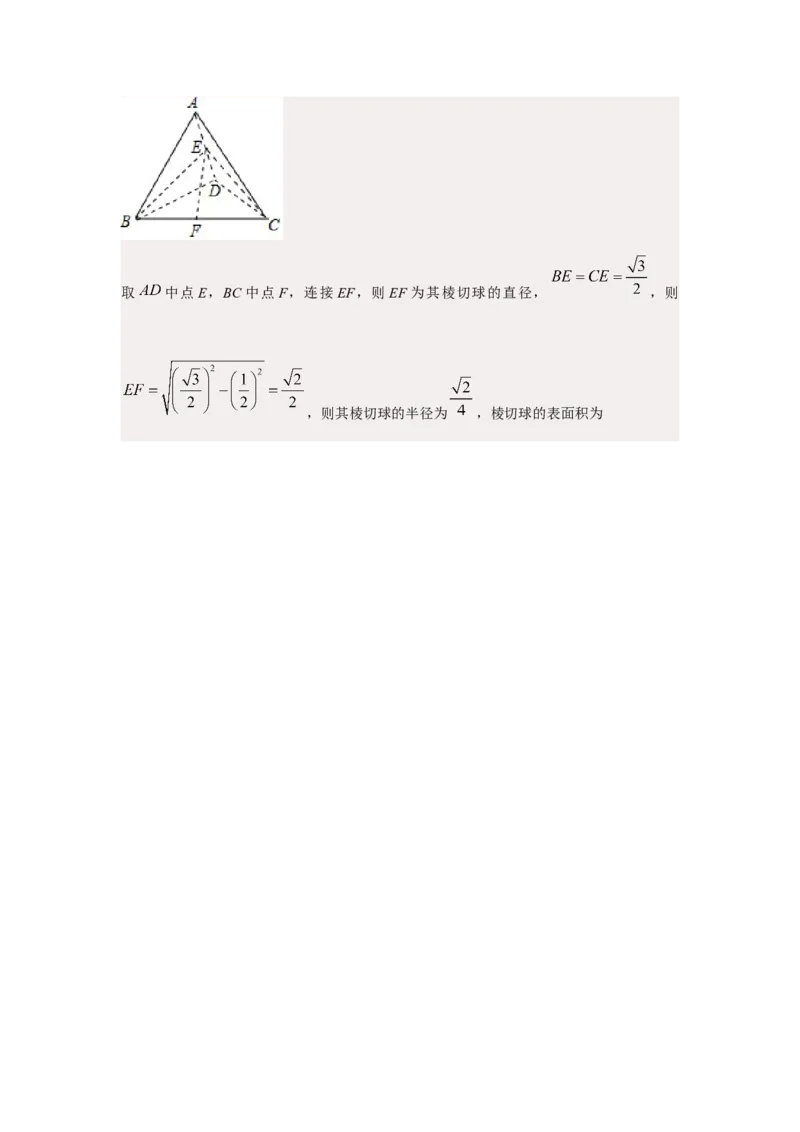
【答案】C
【详解】由题: , , ,所以
.
3.已知向量 ,且 ,则 ( )
A. B. C. 2 D. -2
【答案】D【详解】因为 , ,所以 ,又因为
,所以 ,化简得 .
故选:D.
4.已知函数f(x)=log (6-ax)(a>0,且a≠1)在(0,2)上单调递减,则实数a的取值范围是(
a
)
A.(1,3] B.(1,3)C.(0,1) D.(1,+∞)
【答案】 A
【详解】 令t(x)=6-ax,因为a>0,所以t(x)=6-ax为减函数.
又由函数f(x)=log (6-ax)在(0,2)上单调递减,
a
可得函数t(x)=6-ax>0在(0,2)上恒成立,且a>1,
故有解得10,故由x∈(0,π),得ωx+∈ .
根据函数f(x)在区间(0,π)上恰有三个极值点,知<πω+≤,得<ω≤.
根据函数f(x)在区间(0,π)上恰有两个零点,知2π<πω+≤3π,得<ω≤.
综上,ω的取值范围为
x2 y2
C: − =1(a>0,b>0)
a2 b2
16.已知F为双曲线 的右焦点,A、B是双曲线C的一条渐近
线上关于原点对称的两点,
⃗AF⋅ ⃗BF=0
且线段AF的中点在双曲线C上,则双曲线C的
离心率e= .
【答案】
【详解】因为 为双曲线 的右焦点,所以 .由题知双曲
线的一条渐过线的方程为 ,不妨设 ,则 ,所
以 ,则
,由此得 因此点 的坐标
为 ,线段 的中点坐标为 ,因为它在双曲线上,所以
,化简得 ,解得
四、解答题:共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。c sinA2sinBcosA
17.记△ABC的内角A、B、C的对边分别为a、b、c,且a 2sin A .
(1)求B的大小;b2 2 2 3
(2)若 ,△ABC的面积为 ,求△ABC的周长.
sinC sin A2sinBcosA
【详解】(1)由正弦定理得sinA 2sin A ,所以
sin A2sinBcosA2sinC 2sin(AB)2sin AcosB2cosAsinB
,
sin A2sin AcosB 0 Aπ sinA0
得 ,因为 ,所以 ,
1
cosB
得 2,又0 Bπ,
π
B
所以 3.
1
S acsinB2 3
(2)由 △ABC 2 ,得ac8,
a2 c2 b2 1
cosB
由余弦定理 2ac 2,得a2 c2 8ac,
ac2
3ac832
得 ,
ac4 2
得 ,
ABC 6 2
所以 的周长为 .
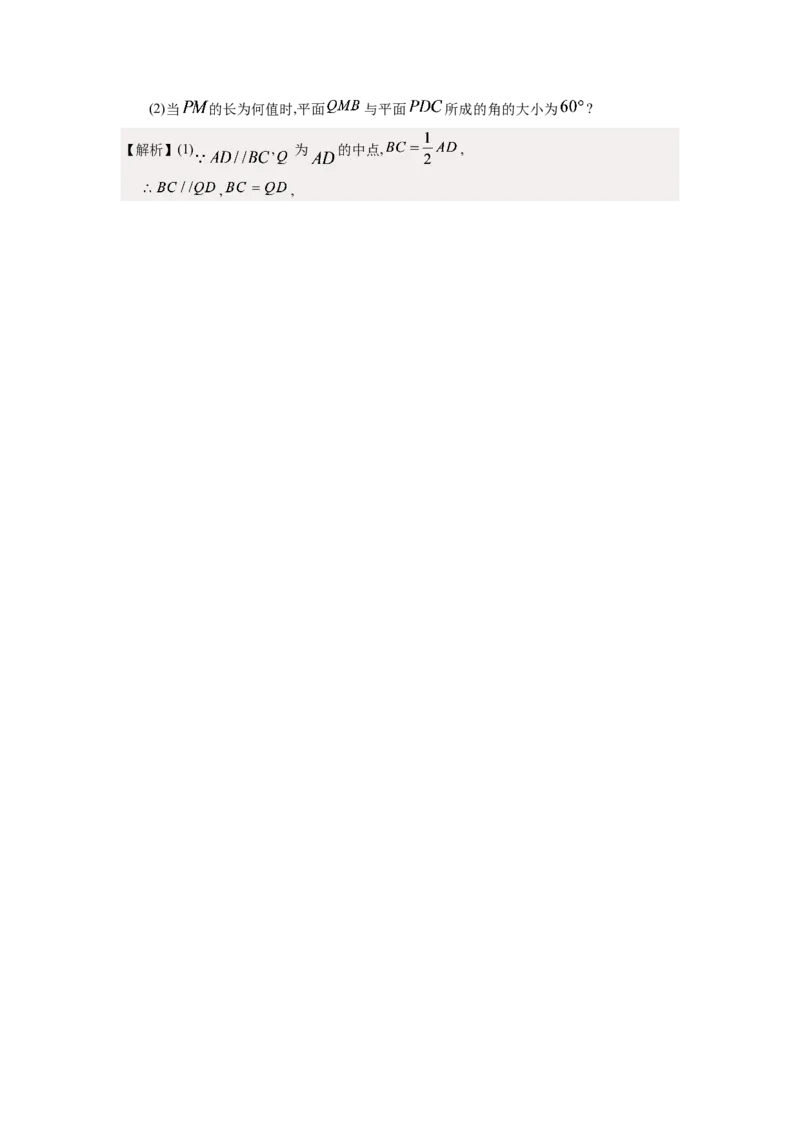
18.如图,在四棱锥 中,底面 为直角梯形, , ,平面
底面 , 为 的中点, 是棱 (不与端点重合)上的点, ,
, .
(1)求证:平面 平面 ;(2)当 的长为何值时,平面 与平面 所成的角的大小为 ?
【解析】(1) , 为 的中点, ,
, ,四边形 为平行四边形, .
, .
, , .
又 平面 平面 ,平面 平面 ,
平面 , .又 , 平面 .
平面 , 平面 平面 .
(2)由(1)可知 平面 .如图,以 为原点,分别以 , , 所在直线为
轴, 轴, 轴,建立空间直角坐标系,
则 , , , , ,
, , , ,
.
设 ,则 ,且 ,得
,
.
设平面 的法向量为 ,
则 ,即 ,
令 ,则 , ,
平面 的一个法向量为 .
设平面 的法向量为 ,则 ,即
令 ,则 , ,平面 的一个法向量为 .
平面 与平面 所成的锐二面角的大小为 ,
,
.
.
即当 时,平面 与平面 所成的角大小为
19.已知函数f(x)=ex-ax-a,a∈R.
(1)讨论f(x)的单调性;
(2)当a=1时,令g(x)=.证明:当x>0时,g(x)>1.
【详解】(1)解 函数f(x)=ex-ax-a的定义域为R,求导得f′(x)=ex-a,
当a≤0时,f′(x)>0恒成立,即f(x)在(-∞,+∞)上单调递增,
当a>0时,令f′(x)=ex-a>0,解得x>ln a,令f′(x)<0,解得x0时,f(x)在(-∞,ln a)上单调递减,在(ln a,+∞)上单调递增.
(2)证明 当a=1时,g(x)=,
当x>0时,>1⇔ex>1+x+⇔<1,
令F(x)=-1,x>0,F′(x)=<0恒成立,则F(x)在(0,+∞)上单调递减,
F(x)0时,g(x)>1,即原不等式得证.
20.已知数列 是以d为公差的等差数列, 为 的前n项和.(1)若 ,求数列 的通项公式;
(2)若 中的部分项组成的数列 是以 为首项,4为公比的等比数列,且 ,
求数列 的前n项和 .
【答案】(1)
(2)
【分析】(1)由 ,可得 ,后由等差数列性质可得公差,即可得通项公式;
(2)由题可得 , .后由 是以d为公差的等差数列, 可得数列
是以 为首项.4为公比的等比数列,可求得数列 的通项公式,后由分组求
和法可得 的前n项和 .
【详解】(1))因为 ,所以 ,
所以 .
所以 .
则数列 的通项公式为 .
(2)因为数列 是以首项为 ,公比为4等比数列.
所以 .因为数列 是等差数列,所以 .
化简得 .
因为 ,所以 ,即 .
所以 .
因为 ,所以数列 是以 为首项.4为公比的等比数列所以 .
所以 .
则数列 的前n项和 为: .
21.甲、乙两选手进行一场体育竞技比赛,采用 局 胜制 的比赛规则,即先
赢下 局比赛者最终获胜. 已知每局比赛甲获胜的概率为 ,乙获胜的概率为 ,比赛
结束时,甲最终获胜的概率为 .
(1)若 ,结束比赛时,比赛的局数为 ,求 的分布列与数学期望;
(2)若采用5局3胜制比采用3局2胜制对甲更有利,即 .
(i)求 的取值范围;
(ii)证明数列 单调递增,并根据你的理解说明该结论的实际含义.
【答案】(1)分布列见解析,
(2)(i) ;(ii)证明见解析,比赛局数越多,对实力较强者越有利
【详解】(1) ,即采用3局2胜制, 所有可能取值为 ,
,
的分布列如下表:
2 3
所以 的数学期望为 .
(2)采用3局2胜制:不妨设赛满3局,用 表示3局比赛中甲胜的局数,则
,甲最终获胜的概率为:
,
采用5局3胜制:不妨设赛满5局,用 表示5局比赛中甲胜的局数,则 ,甲最终获胜的概率为:
,,
得 .
(ii)由(i)知 .
局比赛中恰好甲赢了 局的概率为 ,
局比赛中恰好甲赢了 局的概率为 ,
则 局比赛中甲至少赢 局的概率为 .
考虑 局比赛的前 局:
如果这 局比赛甲至少赢 局,则无论后面结果如何都胜利,其概率为 ,
如果这 局比赛甲赢了 局,则需要后两场至少赢一局,其概率为 ,
如果这 局比赛甲赢了 局,则需要后两场都赢,其概率为 ,
因此 局里甲最终获胜的概率为: ,
因此 ,即数列 单调递增.
该结论的实际意义是:比赛局数越多,对实力较强者越有利.
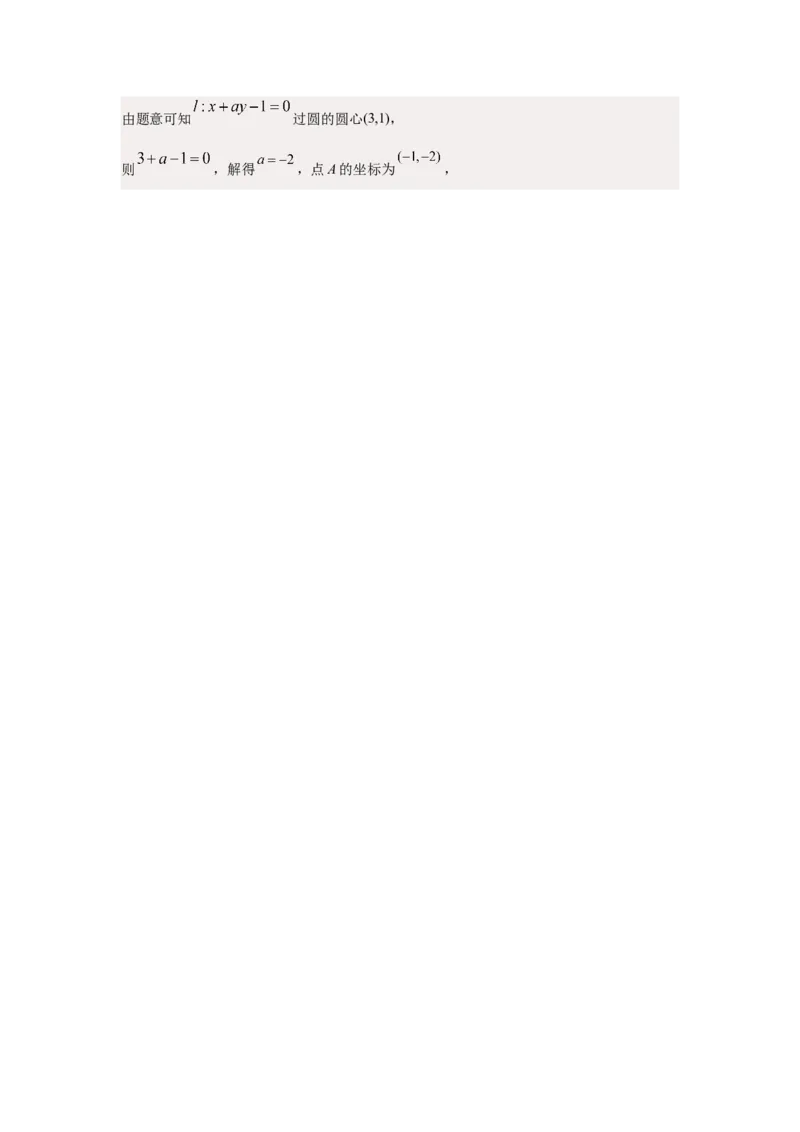
22.已知圆 ,定点 是圆 上的一动点,线段 的垂直平分
线交半径 于点 .
(1)求 的轨迹 的方程;
(2)若过 的直线 分别交轨迹 与 和 ,且直线 的斜率之积为 ,求四
边形 面积的取值范围.
【答案】(1)
(2)【详解】(1)
因为线段 的垂直平分线交半径 与点 ,
所以 ,
所以 是定值, ,
所以 点轨迹为椭圆,其长轴为4,焦距为2,
所以 的轨迹 的方程 .
(2)解法一
设 .由已知得:直线 的方程为 ;
设 , .由已知得:直线 的方程为
又因为AC、BD斜率之积为 ,所以 ,
由 得 ,即 ,
所以 ,
.
故
同理联立BD与椭圆方程,可得 ,
所以 ,
故
设 分别为点 到直线 的距离,则 .又 在直线 在异侧,则
所以 ,
令
易知 ,所以 ,
所以
解法二
设 ,所以 ,设圆心为 ,
因为直线 的斜率之积为 ,
所以 ,
设直线 方程 ,
点 到 的距离为 ,
所以 ,
同理 ,
设四边形 面积为 ,
则 ,
令 ,则 ,所以 ,
所以 ,
设四边形 面积为S,因为 ,
所以 .公众号:高中试卷君