文档内容
专题 14 指数、对数、幂函数、
函数图象、函数零点及函数模型的应用
考点 十年考情(2015-2024) 命题趋势
考点1 指数函数 2023·全国乙卷、2023·全国新Ⅰ卷、2022·北京卷
及其应用 2017·全国、2016·北京、2015·江苏、
(10年5考) 2015·山东卷、2015·福建卷
2024·全国甲卷、2023·北京卷、2022·天津卷
考点2 对数运算 2022·浙江卷、2022·全国乙卷、2021·天津卷
及指对互化 2020·全国卷、2018·全国卷、2016·浙江卷
(10年8考) 2015·浙江卷、2015·浙江卷、2015·四川卷
2015·上海卷、2015·上海卷、2015·安徽卷
1. 掌握指数对数幂函数的图象
考点3 对数函数 2024·北京卷、2024·全国新Ⅰ卷、2020·全国新Ⅱ
与性质,会指数对数的相关运
及其应用 卷2020·全国卷、2020·北京卷、2015·重庆卷
算,会指对幂函数值的大小比
(10年3考) 2015·四川卷、2015·湖北卷、2015·北京卷
较,都是高考命题的方向
考点4 幂函数
2024·天津卷、2023·北京卷、2020·江苏卷 2. 掌握函数图象的判断方法
(10年3考)
3. 掌握函数零点的定义,会用
2024·天津卷、2023·全国甲卷、2023·天津卷
零点存在定理判断零点所在区
2022·天津卷、2022·全国甲卷、2022·全国新Ⅰ卷
间,会求解零点相关问题,也
考点5 指对幂函 2021·天津卷、2021·全国新Ⅱ卷、2020·天津卷
是高考命题的高频考点
数值大小比较 2020·全国卷、2020·全国卷、2020·全国卷
4. 掌握函数模型及其应用
(10年10考) 2019·天津卷、2019·天津卷、2018·天津卷
2017·全国卷、2016·全国卷、2016·全国卷
2015·重庆卷、2015·陕西卷、2015·山东卷
2024·全国甲卷、2023·天津卷、2022·全国乙卷
2022·全国甲卷、2022·天津卷、2021·浙江卷
考点6 函数图象
2020·天津卷、2020·浙江卷、2019·浙江卷
(10年8考)
2018·全国卷、2018·浙江卷、2018·全国卷
2017·全国卷、2017·全国卷、2015·安徽卷2015·浙江卷
2024·全国新Ⅰ卷、2024·全国新Ⅱ卷、2024·全国
新Ⅱ卷、2024·全国甲卷、2024·天津卷、2023·天
津卷、2023·全国新Ⅰ卷、2022·天津卷、2022·北
京卷
2021·北京卷、2021·天津卷、2020·天津卷
考点7 函数零点 2019·全国卷、2019·浙江卷、2019·江苏卷
及其应用 2018·全国卷、2018·浙江卷、2018·天津卷
(10年10考) 2018·全国卷、2017·山东卷、2017·江苏卷
2016·江苏卷、2016·天津卷、2016·天津卷
2016·天津卷、2016·天津卷、2015·天津卷
2015·天津卷、2015·安徽卷、2015·江苏卷
2015·湖北卷、2015·湖北卷、2015·安徽卷
2015·湖南卷、2015·湖南卷
考点8 函数模型 2024·北京卷、2022·北京卷、2021·全国甲卷
(10年5考) 2019·北京卷、2017·北京卷
考点01 指数函数及其应用
1.(2023·全国乙卷·高考真题)已知 是偶函数,则 ( )
A. B. C.1 D.2
2.(2023·全国新Ⅰ卷·高考真题)设函数 在区间 上单调递减,则 的取值范围是( )
A. B.
C. D.
3.(2022·北京·高考真题)已知函数 ,则对任意实数x,有( )
A. B.
C. D.
4.(2017·全国·高考真题)设函数 则满足 的x的取值范围是
.5.(2016·北京·高考真题)下列函数中,在区间 上为减函数的是
A. B. C. D.
6.(2015·江苏·高考真题)不等式 的解集为 .
7.(2015·山东·高考真题)已知函数 的定义域和值域都是 ,则
.
8.(2015·福建·高考真题)若函数 满足 ,且 在 单调递增,
则实数 的最小值等于 .
考点02 对数运算及指对互化
1.(2024·全国甲卷·高考真题)已知 且 ,则 .
2.(2023·北京·高考真题)已知函数 ,则 .
3.(2022·天津·高考真题)化简 的值为( )
A.1 B.2 C.4 D.6
4.(2022·浙江·高考真题)已知 ,则 ( )
A.25 B.5 C. D.
5.(2022·全国乙卷·高考真题)若 是奇函数,则 , .
6.(2021·天津·高考真题)若 ,则 ( )
A. B. C.1 D.
7.(2020·全国·高考真题)设 ,则 ( )
A. B. C. D.
8.(2018·全国·高考真题)已知函数 ,若 ,则 .
9.(2016·浙江·高考真题)已知a>b>1.若logb+log a= ,ab=ba,则a= ,b= .
a b
10.(2015·浙江·高考真题)计算: , .
11.(2015·浙江·高考真题)若 ,则 .12.(2015·四川·高考真题)lg0.01+log 16= .
2
13.(2015·上海·高考真题)方程 的解为 .
14.(2015·上海·高考真题)方程 的解为 .
15.(2015·安徽·高考真题) .
考点03 对数函数及其应用
1.(2024·北京·高考真题)已知 , 是函数 的图象上两个不同的点,则( )
A. B.
C. D.
2.(2024·全国新Ⅰ卷·高考真题)已知函数 在R上单调递增,则a的取值范围是
( )
A. B. C. D.
3.(2020·全国新Ⅱ卷·高考真题)已知函数 在 上单调递增,则 的取值范围是
( )
A. B. C. D.
4.(2020·全国·高考真题)设函数 ,则f(x)( )
A.是偶函数,且在 单调递增 B.是奇函数,且在 单调递减
C.是偶函数,且在 单调递增 D.是奇函数,且在 单调递减
5.(2020·北京·高考真题)函数 的定义域是 .
6.(2015·重庆·高考真题)函数 的定义域是
A.
B.
C.
D.
7.(2015·四川·高考真题)设 , 都是不等于 的正数,则“ ”是“ ”的
A.充要条件 B.充分不必要条件C.必要不充分条件 D.既不充分也不必要条件
8.(2015·湖北·高考真题)函数 的定义域为( )
A. B.
C. D.
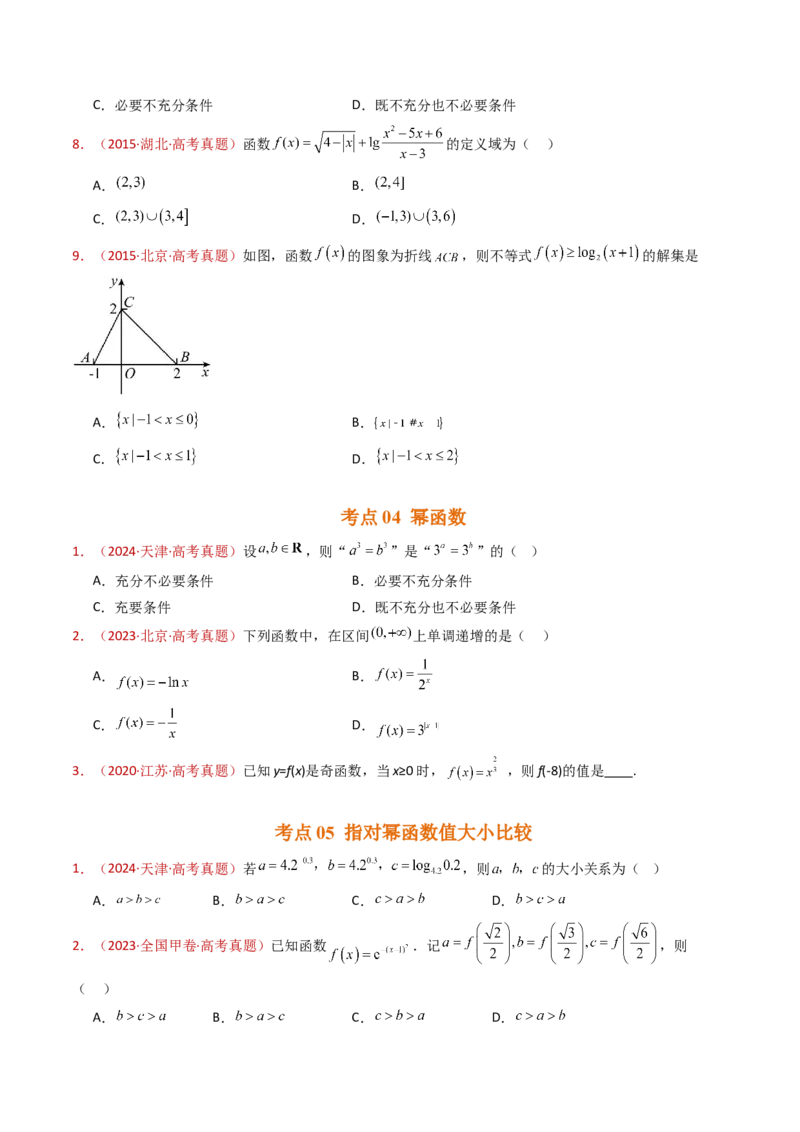
9.(2015·北京·高考真题)如图,函数 的图象为折线 ,则不等式 的解集是
A. B.
C. D.
考点04 幂函数
1.(2024·天津·高考真题)设 ,则“ ”是“ ”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.(2023·北京·高考真题)下列函数中,在区间 上单调递增的是( )
A. B.
C. D.
3.(2020·江苏·高考真题)已知y=f(x)是奇函数,当x≥0时, ,则f(-8)的值是 .
考点05 指对幂函数值大小比较
1.(2024·天津·高考真题)若 ,则 的大小关系为( )
A. B. C. D.
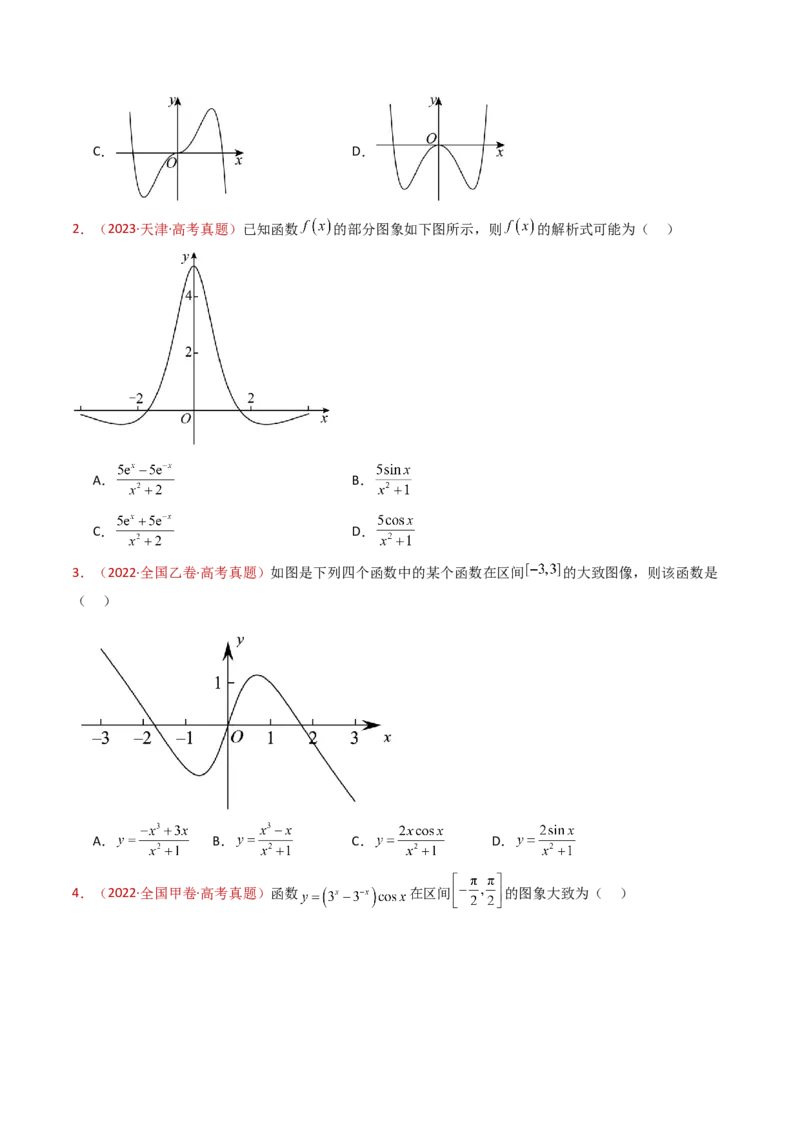
2.(2023·全国甲卷·高考真题)已知函数 .记 ,则
( )
A. B. C. D.3.(2023·天津·高考真题)设 ,则 的大小关系为( )
A. B.
C. D.
4.(2022·天津·高考真题)已知 , , ,则( )
A. B. C. D.
5.(2022·全国甲卷·高考真题)已知 ,则( )
A. B. C. D.
6.(2022·全国新Ⅰ卷·高考真题)设 ,则( )
A. B. C. D.
7.(2021·天津·高考真题)设 ,则a,b,c的大小关系为( )
A. B. C. D.
8.(2021·全国新Ⅱ卷·高考真题)已知 , , ,则下列判断正确的是( )
A. B. C. D.
9.(2020·天津·高考真题)设 ,则 的大小关系为( )
A. B. C. D.
10.(2020·全国·高考真题)已知55<84,134<85.设a=log 3,b=log 5,c=log 8,则( )
5 8 13
A.a