文档内容
焦作市博爱一中 2023—2024 学年高三年级(上)定位考试
数 学
考生注意:
1.开考前,考生务必将自己的姓名、准考证号、座位号填写在试卷和
答题卡上,并将考生号条形码粘贴在答题卡上的指定位置。
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目
的答案标号涂黑。如需要改动,用橡皮檫干净后,再涂选其他答案标号。
回答非选择题时,将答案写在答题卡上。写在试卷上无效。
3.考试结束后,请将本试卷和答题卡一并交回。
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,
只有一项是符合题目要求的.
1. 已知集合 , ,则能使 成立的实数a的
取值的集合是( ).
A. B. C. D.
2. 已知 , , ,若不等式 恒成立,则m的最大值为
( )
A.1 B.2 C.3 D.7
3. 对于问题“求证方程 只有一个解”,可采用如下方法进行证明“将方程
化为 ,设 ,因为 在R上单调递减,
且 ,所以原方程只有一个解 ”.类比上述解题思路,则不等式
的解集是( )
A. B.
C. D.
4. 若复数z所对应的点在第四象限,且满足z2 2z20,则z2 ( )
A.1i B.1i C. D.
5. 埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四
棱锥的高为边长的正方形面积等于该四棱锥侧面积的一半,那么其侧面三角形底边上
学科网(北京)股份有限公司的高与底面正方形的边长的比值为( )
A. B. C. D.
6. 已知四面体 的所有棱长都等于2,E是棱AB的中点,F是棱CD上靠近点C
的四等分点,则 等于( )
A. B. C. D.
7. 已知O为坐标原点,设 , 分别是双曲线 的左、右焦点,P为双曲线
上任一点,过点 作 的平分线的垂线,垂足为H,则 ( )
A.1 B.2 C.4 D.
8. 若对任意正实数x,y都有 ,则实数m的取值范围为(
)
A. B. C.
(,0)[1,)
D.
(,0)[e,)
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有
多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9. 已知集合 有且仅有两个子集,则下列结论正确的是( )
A.
B.
C.若不等式 的解集为 ,则
D.若不等式 的解集为 ,且 ,则
10. 已知 , ,若圆 上存在点M满足
,则实数a可以是( )
A.-1 B. C.0 D.1
11. 已知直线 , , 不能围成三角形,则
实数a的取值可能为( )
学科网(北京)股份有限公司A.1 B. C.-2 D.-1
12. 若定义在R上的函数 ,对任意两个不相等的实数 , ,都有
,则称函数 为“H函数”,下列函数是“H函数”的有(
).
A. B.
C. D.
三、填空题:本大题共4个小题,每小题5分,共20分.
13. 已知 , 则 ________.
14. 正四棱柱 中, 与平面 所成角的正弦值为 ,则异面
直线 与 所成角的余弦值为___________.
15. 已知函数 , ,如果对任意的 , ,都有
成立,则实数a的取值范围是______.
16. 某市教育局人事部门打算将甲、乙、丙、丁、戊这5名应届大学毕业生安排到该市4
所不同的学校任教,每所学校至少安排一名,每名学生只去一所学校,则不同的安排
方法种数是__________.
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)已知函数 ,且 , .
(1)求 的解析式;
(2)判断 在 上的单调性,并用定义证明.
学科网(北京)股份有限公司18. (12分)已知 , , 是同一平面内的三个向量,其中 .
(1)若 ,且 ,求 的坐标;
(2)若 , 与 的夹角为锐角,求实数 的取值范围.
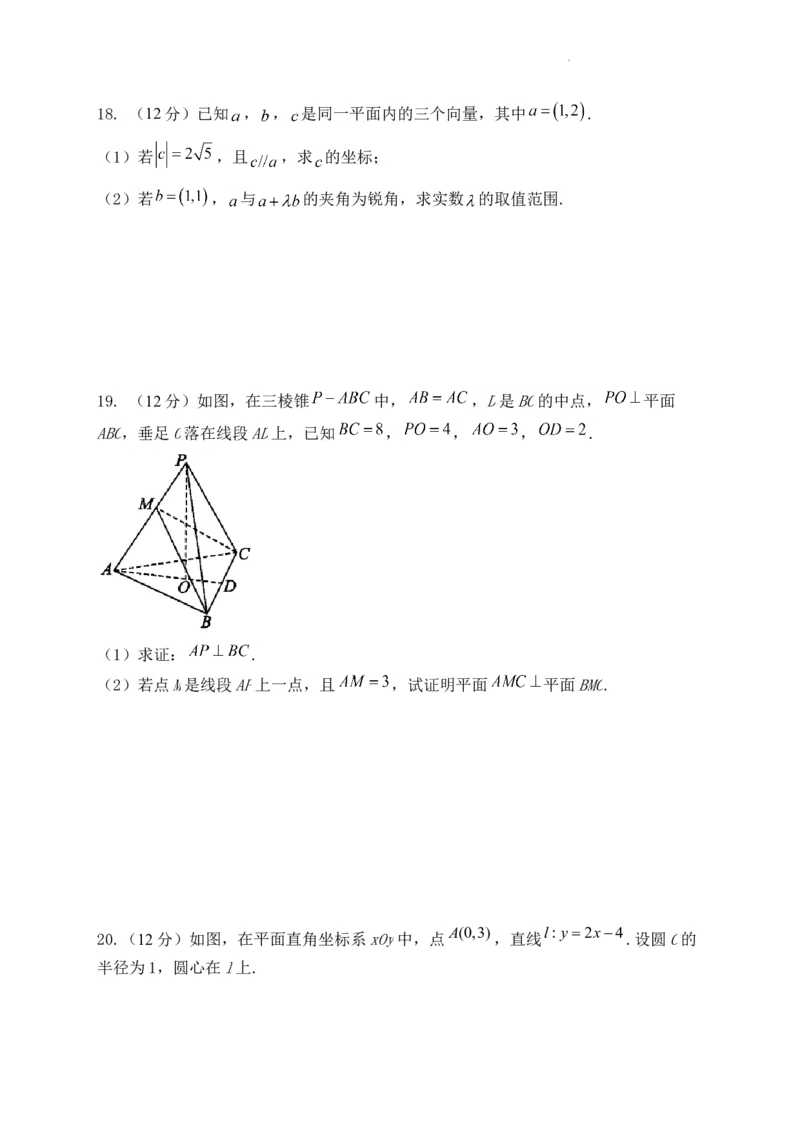
19. (12分)如图,在三棱锥 中, ,D是BC的中点, 平面
ABC,垂足O落在线段AD上,已知 , , , .
(1)求证: .
(2)若点M是线段AP上一点,且 ,试证明平面 平面BMC.
A(0,3) l: y 2x4
20.(12分)如图,在平面直角坐标系xOy中,点 ,直线 .设圆C的
半径为1,圆心在l上.
学科网(北京)股份有限公司(1)若圆心C也在直线 上,过点A作圆C的切线,求切线的方程;
|MA|2|MO|
(2)若圆C上存在点M,使 ,求圆心C的横坐标a的取值范围.
21.(12分)某新建小区规划利用一块空地进行配套绿化.如图,已知空地的一边是直
路AB,余下的外围是抛物线的一段,AB的中垂线恰是该抛物线的对称轴,O是AB的中
点.拟在这块地上划出一个等腰梯形ABCD区域种植草坪,其中A,B,C,D均在该抛物
线上.经测量,直路AB段长为60米,抛物线的顶点P到直路AB的距离为40米.以O为
坐标原点,AB所在直线为x轴建立平面直角坐标系 .
(1)求该段抛物线的方程;
(2)当CD长为多少米时,等腰梯形草坪ABCD的面积最大?
学科网(北京)股份有限公司22.(12分)已知椭圆C的中心为坐标原点,对称轴为x轴,y轴,且过 ,
两点.
(1)求椭圆C的方程;
(2)是否存在直线l,使得直线l与圆 相切,与椭圆C交于A,B两点,且
满足 (O为坐标原点)?若存在,请求出直线l的方程,若不存在,请说明理
由.
学科网(北京)股份有限公司学科网(北京)股份有限公司