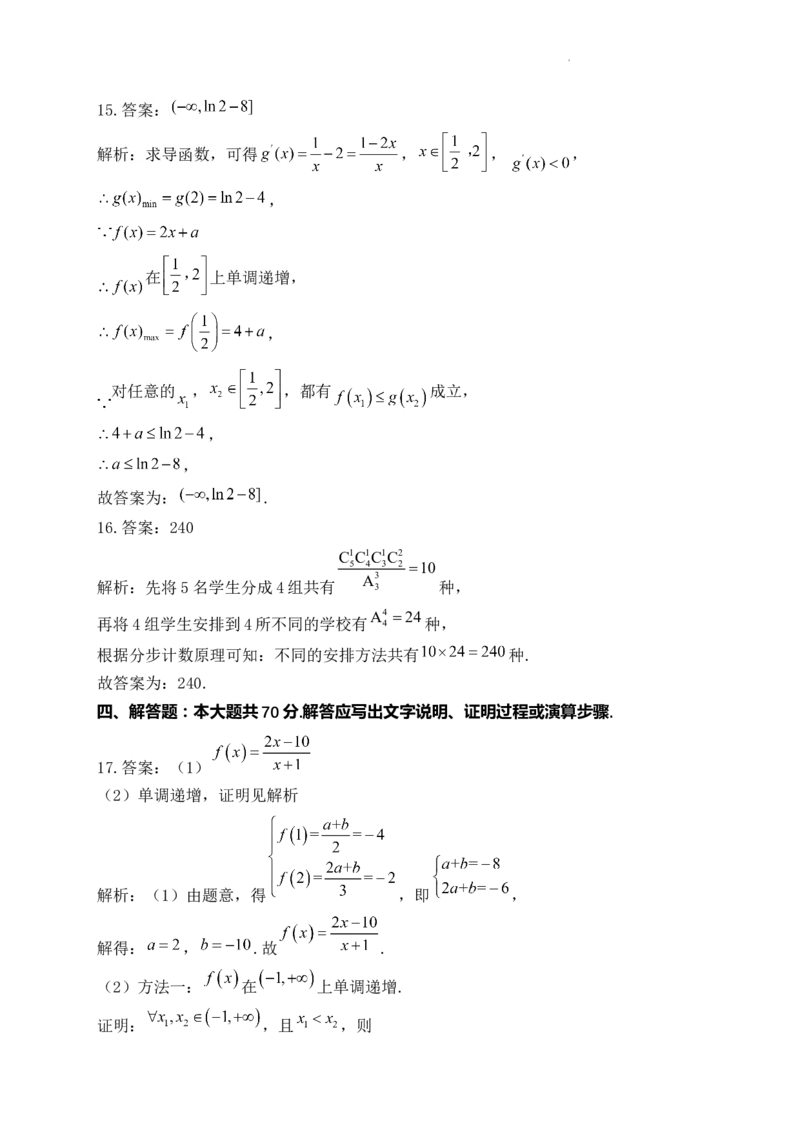焦作市博爱一中2023—2024学年高三年级（上）定位考试数学答案(1)_2023年8月_028月合集_2024届河南省焦作市博爱一中高三年级（上）定位考试

参 考 答 案 一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中， 只有一项是符合题目要求的. 1. 答案：C 解析：解：由 知， 且 ，解得 . 2.答案：C 解析：因为 ，所以 .又因为 ， ，所以 ，当且仅当 时取等号.由 题意可得 ，即 ，则m的最大值为3.故选C. 3.答案：A 解析：由不等式 ， 得 . 设函数 ，则 ， 所以 在R上单调递增. 因为 ， 所以 .解得 或 . 故选：A. 4.答案：C 解析：根据已知有：因为复数z满足： ，即 ，故 或 ，因为复数z所对应的点在第四象限，故复数 ，所以 .故选C. 5.答案：D 解析：设正四棱锥的高为h，底面边长为a，侧面三角形底边上的高为 ，则 由题意可知， ， 学科网（北京）股份有限公司因此有 ， 即 ， 解得 ， 因为 ， 所以 . 所以侧面三角形底边上的高与底面正方形的边长的比值为 . 故选：D. 6.答案：D 解析：因为E是棱AB的中点，F是棱CD上靠近点C的四等分点，所以 ，所以 .因为 ， ， ，所以 .故选D. 7.答案：A 解析：根据双曲线的对称性，不妨在双曲线右支上取点P，延长 ， 交于点Q， 图略.由角平分线性质及 可知 .根据双曲线的定义得， ，从而 ，在 中，OH为其中位线，故 .故选A. 8.答案：A 解析：因为 ， 学科网（北京）股份有限公司所以 ，设 ， ， 则 ， ， 令 恒成立，故 单调递减， 当 时， ，函数 单调递增； 当 时， ，函数 单调递减； 故 所以 ，得到 . 二、多项选择题：本题共 4小题，每小题5分，共20分.在每小题给出的选项中，有 多项符合题目要求.全部选对的得5分，有选错的得0分，部分选对的得2分. 9.答案：ABD 解析：由于集合 有且仅有两个子集，所以 ， .因为 ，所以 . ，当且仅当 ， 时等号成立，故A正确. ，当且仅当 ，即 ， 时等号成立，故B正确.不等式 的解集为 ， 则 ，故C错误.不等式 的解集为 ，即不等式 的解集为 ，且 ，又因为 ， ，所以 ，所以 ，故D 正确.选ABD. 10.答案：ABC 解析： 点M在以AB为直径的圆 上，故问题等价于圆O与圆 C有公共点，所以 ，解得 ，故选ABC. 11.答案：BCD 学科网（北京）股份有限公司解析：因为直线 的斜率为3，直线 的斜率为 ，所以直线 ， 一定相交，交点坐 标是方程组 的解，解得 所以交点坐标为 .当 时，直线 与x 轴垂直，方程为 ，不经过点 ，所以三条直线能围成三角形.当 时，直线 的斜率为 .若直线 与直线 的斜率相等，则 ，即 ，此时这两条直线平 行，因此这三条直线不能围成三角形；若直线 与直线 的斜率相等，则 ，即 ，此时这两条直线平行，因此这三条直线不能围成三角形；若直线 过直线 ， 的交点 ，则 ，即 ，此时三条直线不能围成三角形.故选BCD. 12.答案：BC 解析：由题意可知 是R上的增函数. 对于A，由 f(x)3x2 10 ，得 ，所以 f(x)在区间 上为增函数， 故A中函数不是“H函数”；  π f(x)32(cosxsinx)32 2sinx  对于B，  4，又 ，所以  π f(x)32 2sinx 0  4 恒成立，故B中函数是“H函数”； 对于C， 恒成立，故C中函数是“H函数”； 对于D，易知 f(x)为偶函数，所以它不可能为R上的增函数，故D中函数不是“H函 数”. 三、填空题：每小题5分，共4小题，共20分. 13.答案： 解析：因为 ， ， 所以 ， 所以 学科网（北京）股份有限公司，所以 ， ，所以 ， 则 . 故答案为： . 14.答案： 解析：以A为原点，AB， ， 所在直线分别为x轴、y轴、z轴，建立空间直角 坐标系，如图. 设 ， ，则 ， ， ， ， ，所以 ，平面 的一个法向量 .设 与平面 所成的角为 ，则 ，解得 .所以 ， .设异面直线 与 所成的角为 ，则 . 学科网（北京）股份有限公司15.答案： 解析：求导函数，可得 ， ， ， ， 在 上单调递增， ， 对任意的 ， ，都有 成立， ， ， 故答案为： . 16.答案：240 C1C1C1C2 5 4 3 2 10 A3 解析：先将5名学生分成4组共有 3 种， A4 24 再将4组学生安排到4所不同的学校有 4 种， 根据分步计数原理可知：不同的安排方法共有 种. 故答案为：240. 四、解答题：本大题共70分.解答应写出文字说明、证明过程或演算步骤. 17.答案：（1） （2）单调递增，证明见解析 解析：（1）由题意，得 ，即 ， 解得： ， .故 . （2）方法一： 在 上单调递增. 证明： ，且 ，则 学科网（北京）股份有限公司. 由 ，得 ， ， ， 所以 ，即 .故 在 上单调递增. 方法二： 在 上单调递增. 证明： ，且 ，则 . 由 ，得 ， ，所以 .故 在 上单调递增. 18.答案：（1） 或 （2） 解析：（1）因为 ，且 ， 则 ， 又 ，所以 ，即 ， 故 或 ； （2）由 ，则 ， 由 ，解得 ， 又 与 不共线，则 ，解得 ， 故 与 的夹角为锐角时，实数 的取值范围为： . 19.答案： （1）证明见解析 学科网（北京）股份有限公司（2）证明见解析 解析：（1）因为 ，D是BC的中点，所以 . 如图，以O为原点，过点O作CB的平行线为x轴，以射线AD方向为y轴正方向，以射 线OP的方向为z轴正方向，建立空间直角坐标系， 则 ， ， ， ， ， 所以 ， ， 所以 ， 所以 ，即 . （2）因为 平面 ， 平面ABC，所以 . 因为 ， ，所以 . 因为M为AP上一点，且 ，所以 . 由（1）得 ，所以 . 又 ，所以 . 所以 ， . 设平面BMC的法向量为 ， 则 即 令 ，则 ， ，所以 . 学科网（北京）股份有限公司设平面AMC的法向量为 ， 则 即 令 ，则 ， ，所以 . 所以 ， 所以 ，所以平面 平面BMC. 20.答案： （1） 或 ，即 或  12 0,   （2） 5  C(3,2) 解析：（1）由 得 则圆心 . 又圆C的半径为1，圆C的方程为 . y kx3 kx y30 显然切线的斜率一定存在，设所求圆C的切线方程为 ，即 . ， ， ， 或 . 所求圆C的切线方程为 或 ，即 或 . M(x,y) |MA|2|MO| x2 (y3)2 2 x2  y2 （2）设 ，则由 ，得 ，即 x2 (y1)2 4 x2 (y1)2 4 ，故点M的轨迹方程为 ，记为圆D. 根据题意只要保证圆D与圆C有公共点即可. 12 0a 设 C(a,2a4) ，则 1|DC|3 ，即 1 a2 (2a3)2 3 ，解得 5 .  12 0,   圆心C的横坐标a的取值范围为 5 . 学科网（北京）股份有限公司21.答案：（1） ， （2）20米时，等腰梯形草坪ABCD的面积最大 解析：（1）设该抛物线的方程为y ax2 c，由条件知，B30,0 ，P0,40 ， 所以 ，解得 ，故该段抛物线的方程为 ， . （2）由（1）可设 ，所以梯形ABCD的面积 ， ，设 ， ，则 ，令 ，解得 ，当 时， 在 上是增函数；当 时， 在 上是减函数.所以当 时， 取得极大值，也是最大值.故当CD长为20米时， 等腰梯形草坪ABCD的面积最大. 22.答案：（1） （2）不存在直线l满足题意，理由见解析 解析：（1）设椭圆C的方程为 .因为过 ， 两点，故 解得 ， 所以椭圆C的方程为 . （2）假设存在直线l满足题意. (i)当直线l的斜率不存在时，此时l的方程为 . 当 时， ， ， ， 同理可得，当 时， . 学科网（北京）股份有限公司(ii)当直线l的斜率存在时，设l的方程为 ，设 ， ， 因为直线l与圆O相切，所以 ，即 ①， 联立方程组 整理得 ， ， 由根与系数的关系得 因为 ，所以x x  y y 0. 1 2 1 2 所以 ， 4m2 12 8km 所以  1k2 km m2 0， 34k2 34k2 整理得 ②， 联立①②，得k2 1，此时方程无解. 由(i)(ii)可知，不存在直线l满足题意. 学科网（北京）股份有限公司