文档内容
2022-2023学年小学五年级思维拓展举一反三精编讲义
专题05 周期问题
知识精讲
专题简析:
周期问题是指事物在运动变化的发展过程中,某些特征循环往复出现,其连续两
次出现所经过的时间叫做周期。在数学上,不仅有专门研究周期现象的分支,而且平
时解题时也常常碰到与周期现象有关的问题。这些数学问题只要我们发展某种周期现
象,并充分加以利用,把要求的问题和某一周期的等式相对应,就能找到解题关键。
典例分析
【典例分析01】流水线上生产小木球涂色的次序是:先5个红,再4个黄,再3个绿,再
2个黑,再1个白,然后又依次5红、4黄、3绿、2黑、1白……如此涂下去,到2001个
小球该涂什么颜色?
【思路点拨】根据题意可知,小木球涂色的次序是5红、4黄、3绿、2黑、1白,即
5+4+3+2+1=15个球为一个周期,不断循环。因为 2001÷15=133……6,也就是经过
133个周期还余6个,每个周期中第6个是黄的,所以第2001个球涂黄色。
【典例分析02】有47盏灯,按二盏红灯、四盏蓝灯、三盏黄灯的顺序排列着。最后一盏
灯是什么颜色的?三种颜色的灯各占总数的几分之几?
【思路点拨】(1)我们把二盏红灯、四盏蓝灯、三盏黄灯这 9盏灯看作一组,
47÷9=5(组)……2(盏),余下的两盏是第6组的前两盏灯,是红灯,所以最后一盏灯
是红灯;
(2)由于47÷9=5(组)……2(盏),所以红灯共有2×5+2=12(盏),占总数
的 ;蓝灯共有4×5=20(盏),占总数的 ;黄灯共有3×5=15(盏),占总数的 。
【典例分析03】2001年10月1日是星期一,那么,2002年1月1日是星期几?
【思路点拨】一个星期是7天,因此7天为一个周期。10月1日是星期一,是第一个周期的第一天,再过7天即10月8日也是星期一。计算天数时为了方便,我们采用“算
尾不算头”的方法,例如10月8日就用(8-1)÷7=1,没有余数说明8号仍是星期一。
题中说从2001年10月1日到2002年1月1日,要经过92天,92÷7=13……1,余1天就
是从星期一往后数一天,即星期二。【典例分析04】将奇数如下图排列,各列分别用A、B、C、D、E为代表,问:2001所在
的列以哪个字母为代表?
A B C D E
1 3 5 7
15 13 11 9
17 19 21 23
31 29 27 25
… … … …
… … … …
【思路点拨】这列数按每8个数一组有规律排列着。2001是这一列数中的第1001个
数,1001÷8=125……1,即2001是这列数中第126组的第一个数,所以它所在的那一列是
以字母B为代表的。
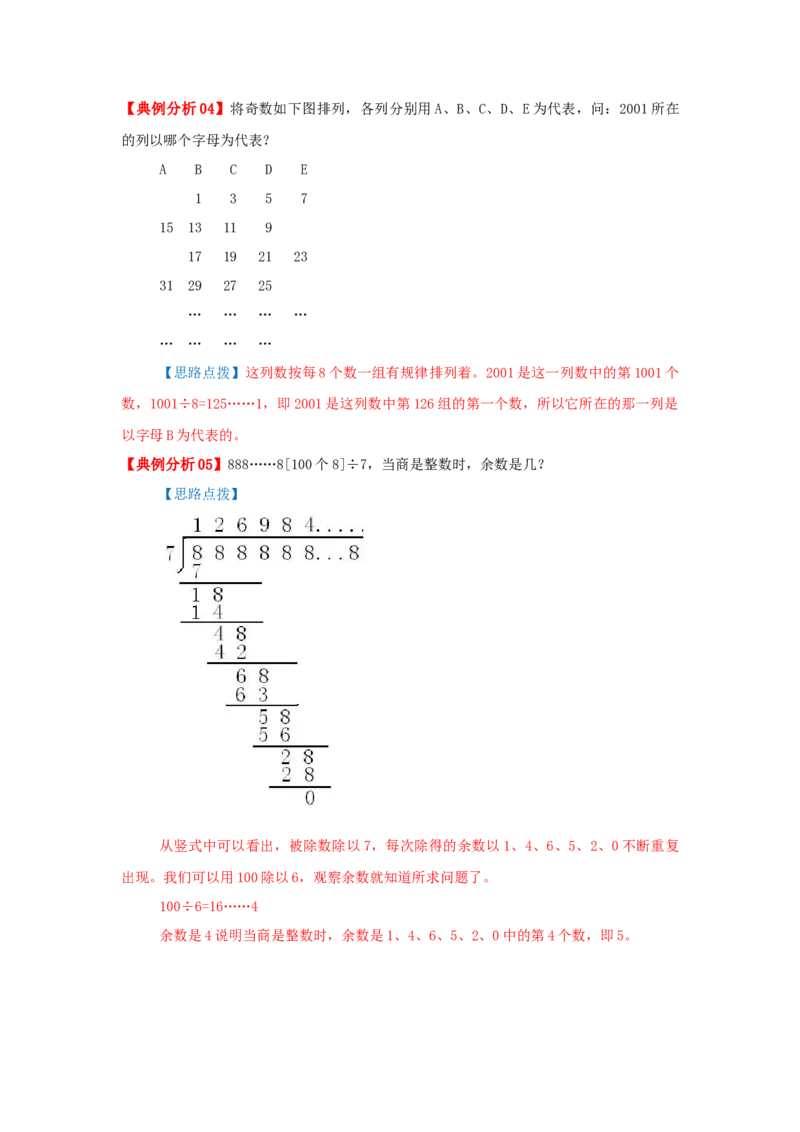
【典例分析05】888……8[100个8]÷7,当商是整数时,余数是几?
【思路点拨】
从竖式中可以看出,被除数除以7,每次除得的余数以1、4、6、5、2、0不断重复
出现。我们可以用100除以6,观察余数就知道所求问题了。
100÷6=16……4
余数是4说明当商是整数时,余数是1、4、6、5、2、0中的第4个数,即5。真题演练
一.选择题(共5小题,满分10分,每小题2分)
1.(2分)三天打鱼,两天晒网(即前三天打鱼,后两天晒网),按照这种方式,在 104
天内,打鱼的天数是( )
A.60 B.61 C.62 D.63
2.(2分)张老师每周的周一、周六和周日都跑步锻炼20分钟,而其余日期每日都跳绳
20分钟.某月他总跑步5小时,那么这个月的第10天是( )
A.周日 B.周六 C.周二 D.周一
3.(2分)在2012年,1月1日是星期日,并且( )
A.1月份有5个星期三,2月份只有4个星期三
B.1月份有5个星期三,2月份也有5个星期三
C.1月份有4个星期三,2月份也有4个星期三
D.1月份有4个星期三,2月份有5个星期三
4.(2分)为了减少城市交通拥堵的情况,某城市拟定从2014年1月1日起开始试行新的
限行规则,规定尾号为1、6的车辆周一、周二限行,尾号2、7的车辆周二、周三限行,
尾号3、8的车辆周三、周四限行,尾号4、9的车辆周四、周五限行,尾号5、0的车辆
周五、周一限行,周六、周日不限行.由于1月31日是春节,因此,1月30日和1月
31日两天不限行.已知2014年1月1日是周三并且限行,那么2014年1月份( )
组尾号可出行的天数最少.
A.1、6 B.2、7 C.4、9 D.5、0
5.(2分)2022年2月22日被广大网民称为“世界最爱日”,因为这个日期里面包含六
个2与它包含相同多2的日期是2022年12月22日,比它包含更多2的日期则是200年
后的2222年2月22日。
今年2月22日又恰好是星期二,200年后的2222年2月22日是星期( )
A.五 B.六 C.一 D.二
E.三
二.填空题(共8小题,满分16分,每小题2分)6.(2分)新年快要到了,乐乐想要通过自己的努力攒钱给妈妈买礼物。于是打算每天存
2元钱,每攒10天就要休息1天不存钱,并且在休息的这一天花4元钱给自己买一只棒
棒糖作为奖励,那么乐乐攒够80元最少需要 天。
7.(2分)某班40名学生全都面向前方,从前向后站成一列,按照 1、2、3、4、1、2、
3、4、…的顺序循环报数,每人报一次数,报到 3的同学向后转.之后,如果相邻两个
学生面对面,他们就会握一次手,然后同时向后转,一直到不再有学生面对面.那么,
整个过程中,全班同学一共握手了 次.
8.(2分)在中国古代的历法中,甲、乙、丙、丁、戊、己、庚、辛、壬、癸被称为“十
天干”,子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥叫作“十二地支”;十天
干和十二地支进行循环组合:甲子、乙丑、丙寅.一直到癸亥,共得到60个组合,称
为六十甲子.如此周而复始用来纪年的方法,称为甲子纪年法在甲子纪年中,以“丑”
结尾的年份除了“乙丑”外,还有 .
9.(2分)四年一班的22名男生、33名女生在操场上站队,老师先让所有同学按照2名
男生、3名女生、2名男生、3名女生……的顺序从左至右站成一排。第一次从左向右依
次报数,第二次从右向左依次报数,每次都是从1报到
55。那么从右向左数的第20名女生两次所报的数之差为 。
10.(2分)一个月最多有5个星期日,在一年的12个月中,有5个星期日的月份最多有
个月.
11.(2分)2021年10月25日星期一,中央广播电视总台央视奥林匹克频道及其数字平
台开播上线,2022年2月4日北京冬奥会开幕,那么北京冬奥会开幕这一天是星期
。
12.(2分)数列:1、3、3、4、11、13、13、……,是从1开始,依次加2、加0、加
1、加7并循环往复所形成.那么,当这个数列中第一次出现恰好由2、0、1、7这四个
数字(不一定按顺序)所组成的四位数时,这个数列已经写了 个数.
13.(2分)2018年11月份的日历上,有一列5个日期的数字和为75,已知这一列的第一
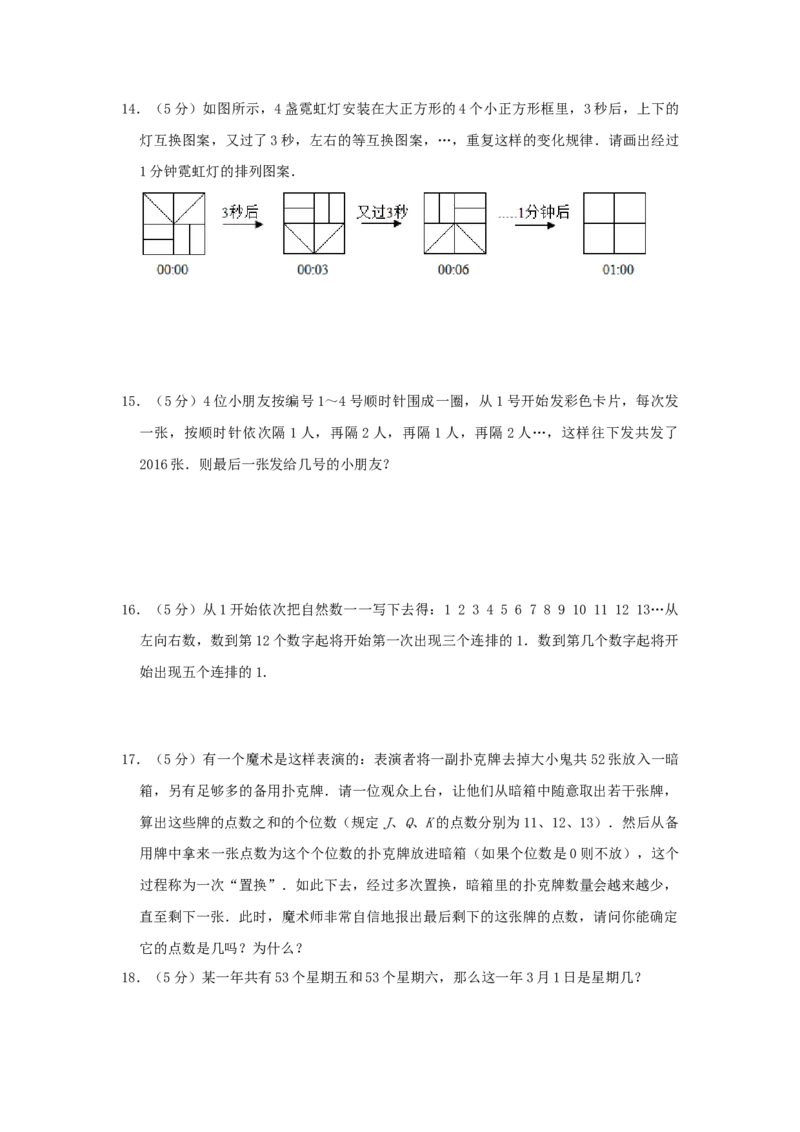
个日期那天是星期四,那么这个月的10号是星期 。三.解答题(共15小题,满分75分,每小题5分)14.(5分)如图所示,4盏霓虹灯安装在大正方形的4个小正方形框里,3秒后,上下的
灯互换图案,又过了3秒,左右的等互换图案,…,重复这样的变化规律.请画出经过
1分钟霓虹灯的排列图案.
15.(5分)4位小朋友按编号1~4号顺时针围成一圈,从1号开始发彩色卡片,每次发
一张,按顺时针依次隔1人,再隔2人,再隔1人,再隔2人…,这样往下发共发了
2016张.则最后一张发给几号的小朋友?
16.(5分)从1开始依次把自然数一一写下去得:1 2 3 4 5 6 7 8 9 10 11 12 13…从
左向右数,数到第12个数字起将开始第一次出现三个连排的1.数到第几个数字起将开
始出现五个连排的1.
17.(5分)有一个魔术是这样表演的:表演者将一副扑克牌去掉大小鬼共52张放入一暗
箱,另有足够多的备用扑克牌.请一位观众上台,让他们从暗箱中随意取出若干张牌,
算出这些牌的点数之和的个位数(规定J、Q、K的点数分别为11、12、13).然后从备
用牌中拿来一张点数为这个个位数的扑克牌放进暗箱(如果个位数是0则不放),这个
过程称为一次“置换”.如此下去,经过多次置换,暗箱里的扑克牌数量会越来越少,
直至剩下一张.此时,魔术师非常自信地报出最后剩下的这张牌的点数,请问你能确定
它的点数是几吗?为什么?
18.(5分)某一年共有53个星期五和53个星期六,那么这一年3月1日是星期几?19.(5分)如图一个3×3的网格中填好了数,定义一次操作:讲这个表中的一行或一列
或一条对角线上的数减去或加上同一个自然数.请你判断能否经过有限次操作,使得这
9个数相等?如果能,请指出最少操作的次数;如果不能,请答0.你的结论是 .
20.(5分)将乘积 化为小数,小数点后第2013位的数字是 .
21.(5分)2012年的6月9日是星期六,问:2011年的6月9日是星期几?
22.(5分)某年的2月有5个星期五,那么这年的1月31日是星期 .23.(5分)2009年的元旦是星期四,问:在2009年中,哪几个月的第一天也是星期四?
哪几个月有5个星期日?
24.(5分)将分数 化成纯小数后,小数点后至少多少个数字之和是2017?这时a是几?
25.(5分)一本历史书共有2640页,张强每小时阅读16页.第一日到第十日,每日读5
小时;第十一日到第二十日,每日读6小时;第二十一日到最后一日的前一日,每日读
7小时.经过若干日全部读完.问:最后一日是第几日?最后一日读了几小时?
26.(5分)有158个小朋友排成一排,从左边第一个人起(第一个人发一个苹果),每
隔1人发一个苹果,又从右边第一个人起(第一个人发一个香蕉),每隔 2人发一个香
蕉,求没有得到水果的小朋友的人数.
27.(5分)一只用黑、白两种颜色的皮子缝制成的足球如图所示.已知这只足球上有黑
色皮子l2块.问:这只足球上缝了多少块白色皮子?请简述理由.28.(5分)2012位同学排成一列依次报数.若某位同学报的是一位数,后面的同学就报
这个数的2倍;若某位同学报的是两位数,后面的同学就报其个位数字与5的和.已知
第一位同学报1.
(1)那么第2012位同学所报的数是多少?
(2)到了第100位同学,他却把前面那位同学报的数加上了另一个一位自然数,其他
人都没有注意到,仍然按以前的规则继续报数,直到最后一位同学报的数是5.那么第
100位同学所报的数是把前一位同学报的数加上了多少?