文档内容
五年(2019-2023)年高考真题分项汇编
专题 05 立体几何(理科)(选填题)
立体几何在文科数高考中属于重点知识点,难度中等。包含题型主要是
1 空间几何体基本性质及表面积体积
2 空间几何题三视图
3 空间几何体内切球外接球的应用
4 空间几何体情景化应用
考点 01 空间几何体基本性质及表面积体积
一、单选题
1.(2023·全国·统考乙卷)已知圆锥PO的底面半径为 ,O为底面圆心,PA,PB为圆锥的母线,
,若 的面积等于 ,则该圆锥的体积为( )
A. B. C. D.
【答案】B
【分析】根据给定条件,利用三角形面积公式求出圆锥的母线长,进而求出圆锥的高,求出体积作答.
【详解】在 中, ,而 ,取 中点 ,连接 ,有
,如图,
, ,由 的面积为 ,得 ,
1解得 ,于是 ,
所以圆锥的体积 .
故选:B
2.(2023·全国·统考甲卷)已知四棱锥 的底面是边长为4的正方形, ,
则 的面积为( )
A. B. C. D.
【答案】C
【分析】法一:利用全等三角形的证明方法依次证得 , ,从而得到 ,
再在 中利用余弦定理求得 ,从而求得 ,由此在 中利用余弦定理与三角形面
积公式即可得解;
法二:先在 中利用余弦定理求得 , ,从而求得 ,再利用空间向
量的数量积运算与余弦定理得到关于 的方程组,从而求得 ,由此在 中利用余弦定
理与三角形面积公式即可得解.
【详解】法一:
连结 交于 ,连结 ,则 为 的中点,如图,
因为底面 为正方形, ,所以 ,则 ,
又 , ,所以 ,则 ,
又 , ,所以 ,则 ,
在 中, ,
则由余弦定理可得 ,
故 ,则 ,
故在 中, ,
2所以 ,
又 ,所以 ,
所以 的面积为 .
法二:
连结 交于 ,连结 ,则 为 的中点,如图,
因为底面 为正方形, ,所以 ,
在 中, ,
则由余弦定理可得 ,故 ,
所以 ,则
,
不妨记 ,
因为 ,所以 ,
即 ,
则 ,整理得 ①,
又在 中, ,即 ,则
②,
两式相加得 ,故 ,
故在 中, ,
所以 ,
又 ,所以 ,
3所以 的面积为 .
故选:C.
3.(2023·天津·统考高考真题)在三棱锥 中,线段 上的点 满足 ,线段 上的
点 满足 ,则三棱锥 和三棱锥 的体积之比为( )
A. B. C. D.
【答案】B
【分析】分别过 作 ,垂足分别为 .过 作 平面 ,垂足为 ,连接
,过 作 ,垂足为 .先证 平面 ,则可得到 ,再证 .由三角形相
似得到 , ,再由 即可求出体积比.
【详解】如图,分别过 作 ,垂足分别为 .过 作 平面 ,垂足为 ,
连接 ,过 作 ,垂足为 .
因为 平面 , 平面 ,所以平面 平面 .
又因为平面 平面 , , 平面 ,所以 平面 ,且 .
在 中,因为 ,所以 ,所以 ,
在 中,因为 ,所以 ,
所以 .
故选:B
44.(2022·全国·统考高考乙卷)在正方体 中,E,F分别为 的中点,则( )
A.平面 平面 B.平面 平面
C.平面 平面 D.平面 平面
【答案】A
【分析】证明 平面 ,即可判断A;如图,以点 为原点,建立空间直角坐标系,设 ,分
别求出平面 , , 的法向量,根据法向量的位置关系,即可判断BCD.
【详解】解:在正方体 中,
且 平面 ,
又 平面 ,所以 ,
因为 分别为 的中点,
所以 ,所以 ,
又 ,
所以 平面 ,
又 平面 ,
所以平面 平面 ,故A正确;
选项BCD解法一:
如图,以点 为原点,建立空间直角坐标系,设 ,
则 ,
,
则 , ,
设平面 的法向量为 ,
则有 ,可取 ,
同理可得平面 的法向量为 ,
平面 的法向量为 ,
平面 的法向量为 ,
则 ,
所以平面 与平面 不垂直,故B错误;
5因为 与 不平行,
所以平面 与平面 不平行,故C错误;
因为 与 不平行,
所以平面 与平面 不平行,故D错误,
故选:A.
选项BCD解法二:
解:对于选项B,如图所示,设 , ,则 为平面 与平面 的交线,
在 内,作 于点 ,在 内,作 ,交 于点 ,连结 ,
则 或其补角为平面 与平面 所成二面角的平面角,
由勾股定理可知: , ,
底面正方形 中, 为中点,则 ,
由勾股定理可得 ,
从而有: ,
据此可得 ,即 ,
据此可得平面 平面 不成立,选项B错误;
对于选项C,取 的中点 ,则 ,
6由于 与平面 相交,故平面 平面 不成立,选项C错误;
对于选项D,取 的中点 ,很明显四边形 为平行四边形,则 ,
由于 与平面 相交,故平面 平面 不成立,选项D错误;
故选:A.
5.(2022·全国·统考高考甲卷)甲、乙两个圆锥的母线长相等,侧面展开图的圆心角之和为 ,侧面积分
别为 和 ,体积分别为 和 .若 ,则 ( )
A. B. C. D.
【答案】C
【分析】设母线长为 ,甲圆锥底面半径为 ,乙圆锥底面圆半径为 ,根据圆锥的侧面积公式可得 ,
再结合圆心角之和可将 分别用 表示,再利用勾股定理分别求出两圆锥的高,再根据圆锥的体积公式即
可得解.
【详解】解:设母线长为 ,甲圆锥底面半径为 ,乙圆锥底面圆半径为 ,
则 ,
所以 ,
7又 ,
则 ,
所以 ,
所以甲圆锥的高 ,
乙圆锥的高 ,
所以 .
故选:C.
6.(2022·北京·统考高考真题)已知正三棱锥 的六条棱长均为6,S是 及其内部的点构成的
集合.设集合 ,则T表示的区域的面积为( )
A. B. C. D.
【答案】B
【分析】求出以 为球心,5为半径的球与底面 的截面圆的半径后可求区域的面积.
【详解】
设顶点 在底面上的投影为 ,连接 ,则 为三角形 的中心,
且 ,故 .
因为 ,故 ,
故 的轨迹为以 为圆心,1为半径的圆,
而三角形 内切圆的圆心为 ,半径为 ,
8故 的轨迹圆在三角形 内部,故其面积为
故选:B
7.(2021·全国·统考高考Ⅰ卷)已知圆锥的底面半径为 ,其侧面展开图为一个半圆,则该圆锥的母线
长为( )
A. B. C. D.
【答案】B
【分析】设圆锥的母线长为 ,根据圆锥底面圆的周长等于扇形的弧长可求得 的值,即为所求.
【详解】设圆锥的母线长为 ,由于圆锥底面圆的周长等于扇形的弧长,则 ,解得 .
故选:B.
8.(2019·全国·统考高考Ⅲ卷)如图,点 为正方形 的中心, 为正三角形,平面 平面
是线段 的中点,则
A. ,且直线 是相交直线
B. ,且直线 是相交直线
C. ,且直线 是异面直线
D. ,且直线 是异面直线
【答案】B
【解析】利用垂直关系,再结合勾股定理进而解决问题.
【详解】如图所示, 作 于 ,连接 ,过 作 于 .
连 , 平面 平面 .
平面 , 平面 , 平面 ,
与 均为直角三角形.设正方形边长为2,易知 ,
. ,故选B.
9【点睛】本题考查空间想象能力和计算能力, 解答本题的关键是构造直角三角形.
二、填空题
9.(2023·全国新高考·Ⅱ卷)底面边长为4的正四棱锥被平行于其底面的平面所截,截去一个底面边长为
2,高为3的正四棱锥,所得棱台的体积为 .
【答案】
【分析】方法一:割补法,根据正四棱锥的几何性质以及棱锥体积公式求得正确答案;方法二:根据台体
的体积公式直接运算求解.
【详解】方法一:由于 ,而截去的正四棱锥的高为 ,所以原正四棱锥的高为 ,
所以正四棱锥的体积为 ,
截去的正四棱锥的体积为 ,
所以棱台的体积为 .
方法二:棱台的体积为 .
故答案为: .
10.(2020·全国·新高考Ⅱ卷)已知正方体ABCD-A B C D 的棱长为2,M、N分别为BB 、AB的中点,则三
1 1 1 1 1
棱锥A-NMD 的体积为
1
【答案】
10【分析】利用 计算即可.
【详解】
因为正方体ABCD-A B C D 的棱长为2,M、N分别为BB 、AB的中点
1 1 1 1 1
所以
故答案为:
【点睛】在求解三棱锥的体积时,要注意观察图形的特点,看把哪个当成顶点好计算一些.
11.(2020·全国·统考高考Ⅱ卷)设有下列四个命题:
p :两两相交且不过同一点的三条直线必在同一平面内.
1
p :过空间中任意三点有且仅有一个平面.
2
p :若空间两条直线不相交,则这两条直线平行.
3
p :若直线l 平面α,直线m⊥平面α,则m⊥l.
4
则下述命题中所有真命题的序号是 .
① ② ③ ④
【答案】①③④
【分析】利用两交线直线确定一个平面可判断命题 的真假;利用三点共线可判断命题 的真假;利用异
面直线可判断命题 的真假,利用线面垂直的定义可判断命题 的真假.再利用复合命题的真假可得出结
论.
【详解】对于命题 ,可设 与 相交,这两条直线确定的平面为 ;
若 与 相交,则交点 在平面 内,
同理, 与 的交点 也在平面 内,
所以, ,即 ,命题 为真命题;
11对于命题 ,若三点共线,则过这三个点的平面有无数个,
命题 为假命题;
对于命题 ,空间中两条直线相交、平行或异面,
命题 为假命题;
对于命题 ,若直线 平面 ,
则 垂直于平面 内所有直线,
直线 平面 , 直线 直线 ,
命题 为真命题.
综上可知, , 为真命题, , 为假命题,
为真命题, 为假命题,
为真命题, 为真命题.
故答案为:①③④.
【点睛】本题考查复合命题的真假,同时也考查了空间中线面关系有关命题真假的判断,考查推理能力,
属于中等题.
考点 02 空间几何体三视图
一、单选题
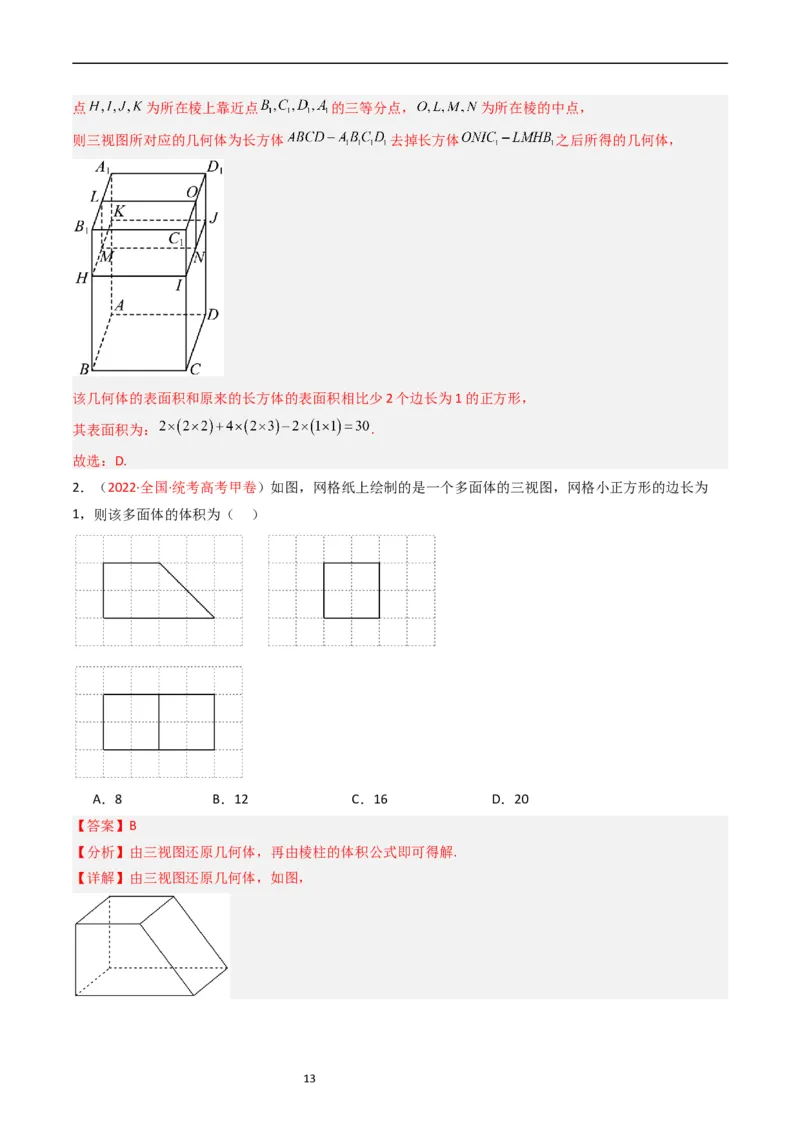
1.(2023·全国·统考高考乙卷)如图,网格纸上绘制的一个零件的三视图,网格小正方形的边长为1,则
该零件的表面积为( )
A.24 B.26 C.28 D.30
【答案】D
【分析】由题意首先由三视图还原空间几何体,然后由所得的空间几何体的结构特征求解其表面积即可.
【详解】如图所示,在长方体 中, , ,
12点 为所在棱上靠近点 的三等分点, 为所在棱的中点,
则三视图所对应的几何体为长方体 去掉长方体 之后所得的几何体,
该几何体的表面积和原来的长方体的表面积相比少2个边长为1的正方形,
其表面积为: .
故选:D.
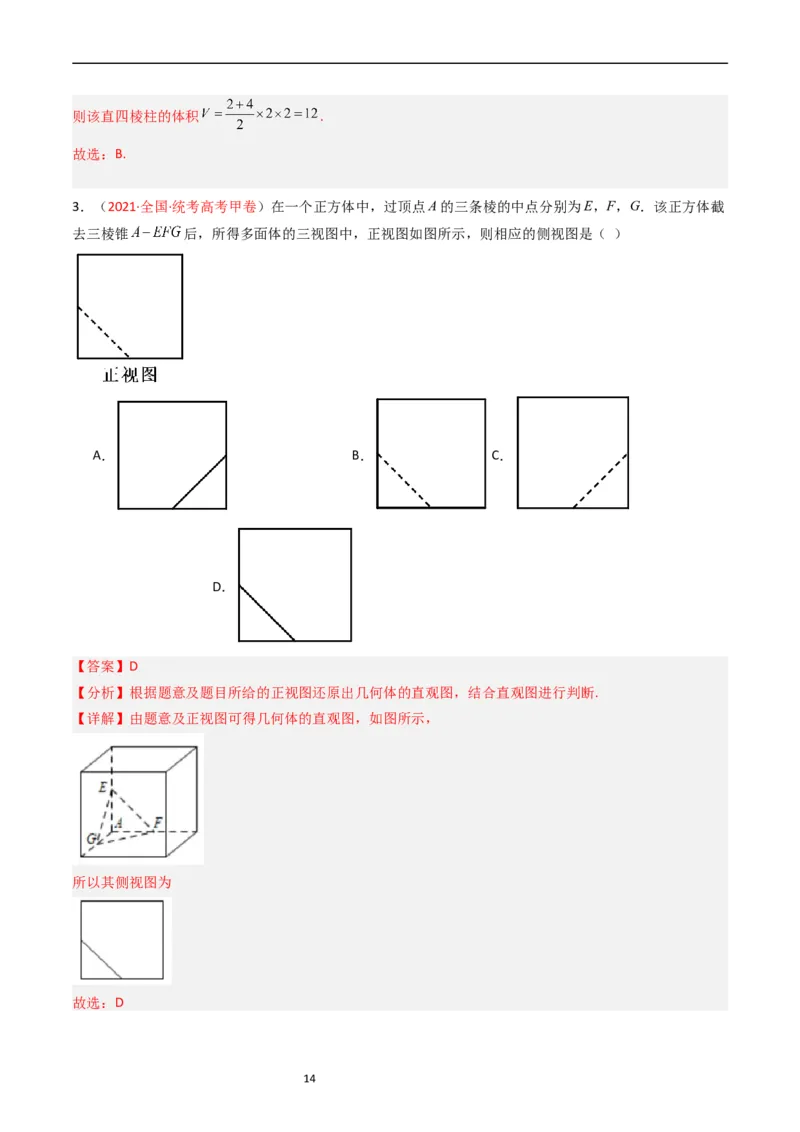
2.(2022·全国·统考高考甲卷)如图,网格纸上绘制的是一个多面体的三视图,网格小正方形的边长为
1,则该多面体的体积为( )
A.8 B.12 C.16 D.20
【答案】B
【分析】由三视图还原几何体,再由棱柱的体积公式即可得解.
【详解】由三视图还原几何体,如图,
13则该直四棱柱的体积 .
故选:B.
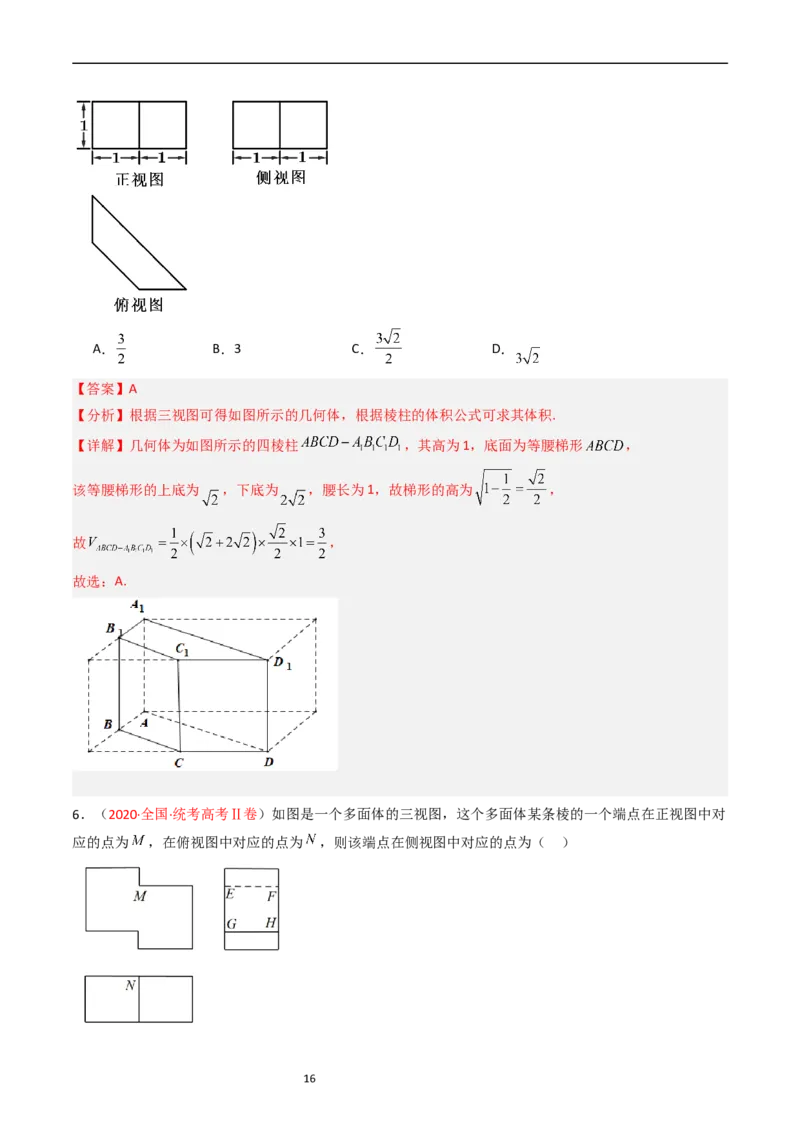
3.(2021·全国·统考高考甲卷)在一个正方体中,过顶点A的三条棱的中点分别为E,F,G.该正方体截
去三棱锥 后,所得多面体的三视图中,正视图如图所示,则相应的侧视图是( )
A. B. C.
D.
【答案】D
【分析】根据题意及题目所给的正视图还原出几何体的直观图,结合直观图进行判断.
【详解】由题意及正视图可得几何体的直观图,如图所示,
所以其侧视图为
故选:D
144.(2021·北京·统考高考真题)某四面体的三视图如图所示,该四面体的表面积为( )
A. B. C. D.
【答案】A
【分析】根据三视图可得如图所示的几何体(三棱锥),根据三视图中的数据可计算该几何体的表面积.
【详解】根据三视图可得如图所示的几何体-正三棱锥 ,
其侧面为等腰直角三角形,底面等边三角形,
由三视图可得该正三棱锥的侧棱长为1,
故其表面积为 ,
故选:A.
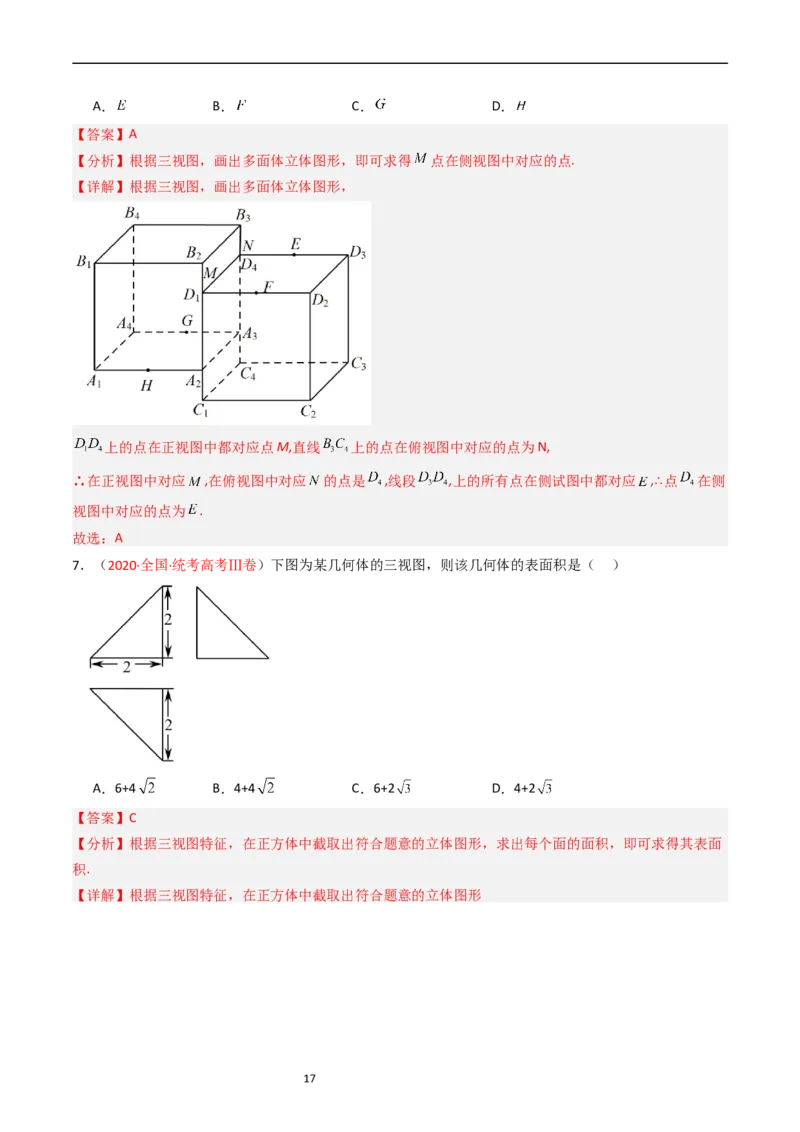
5.(2021·浙江·统考高考真题)某几何体的三视图如图所示,则该几何体的体积是( )
15A. B.3 C. D.
【答案】A
【分析】根据三视图可得如图所示的几何体,根据棱柱的体积公式可求其体积.
【详解】几何体为如图所示的四棱柱 ,其高为1,底面为等腰梯形 ,
该等腰梯形的上底为 ,下底为 ,腰长为1,故梯形的高为 ,
故 ,
故选:A.
6.(2020·全国·统考高考Ⅱ卷)如图是一个多面体的三视图,这个多面体某条棱的一个端点在正视图中对
应的点为 ,在俯视图中对应的点为 ,则该端点在侧视图中对应的点为( )
16A. B. C. D.
【答案】A
【分析】根据三视图,画出多面体立体图形,即可求得 点在侧视图中对应的点.
【详解】根据三视图,画出多面体立体图形,
上的点在正视图中都对应点M,直线 上的点在俯视图中对应的点为N,
∴在正视图中对应 ,在俯视图中对应 的点是 ,线段 ,上的所有点在侧试图中都对应 ,∴点 在侧
视图中对应的点为 .
故选:A
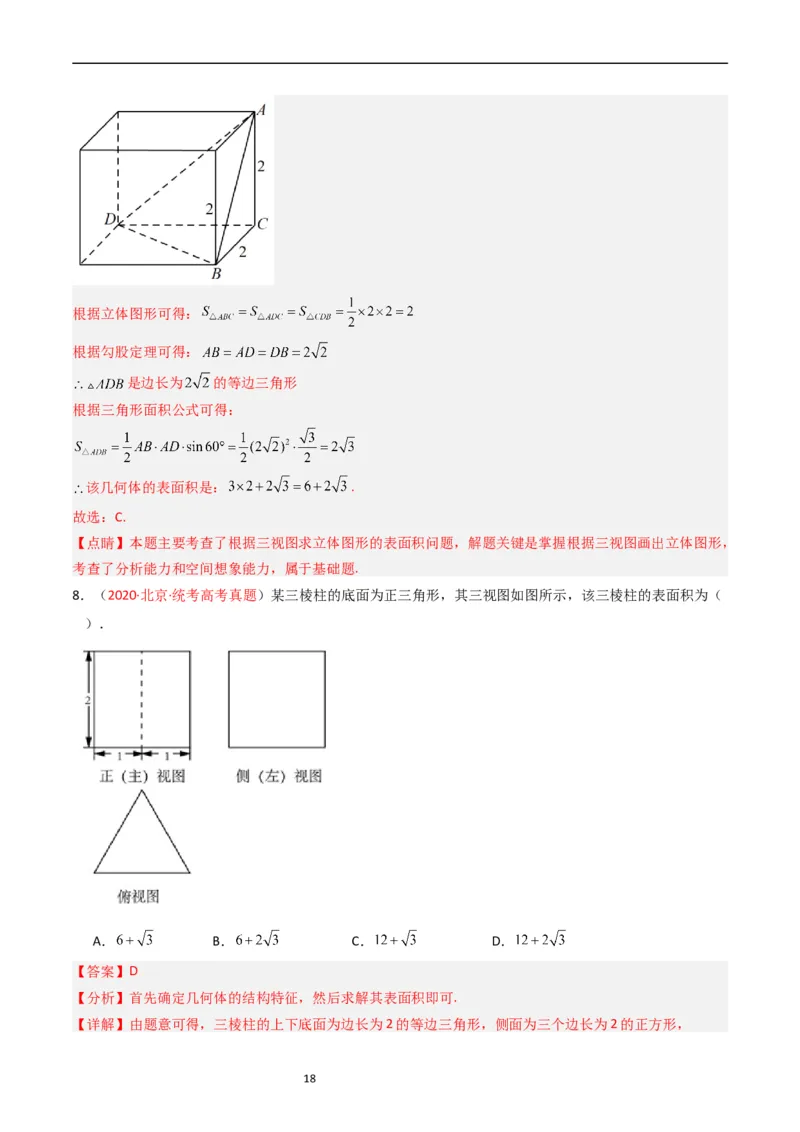
7.(2020·全国·统考高考Ⅲ卷)下图为某几何体的三视图,则该几何体的表面积是( )
A.6+4 B.4+4 C.6+2 D.4+2
【答案】C
【分析】根据三视图特征,在正方体中截取出符合题意的立体图形,求出每个面的面积,即可求得其表面
积.
【详解】根据三视图特征,在正方体中截取出符合题意的立体图形
17根据立体图形可得:
根据勾股定理可得:
是边长为 的等边三角形
根据三角形面积公式可得:
该几何体的表面积是: .
故选:C.
【点睛】本题主要考查了根据三视图求立体图形的表面积问题,解题关键是掌握根据三视图画出立体图形,
考查了分析能力和空间想象能力,属于基础题.
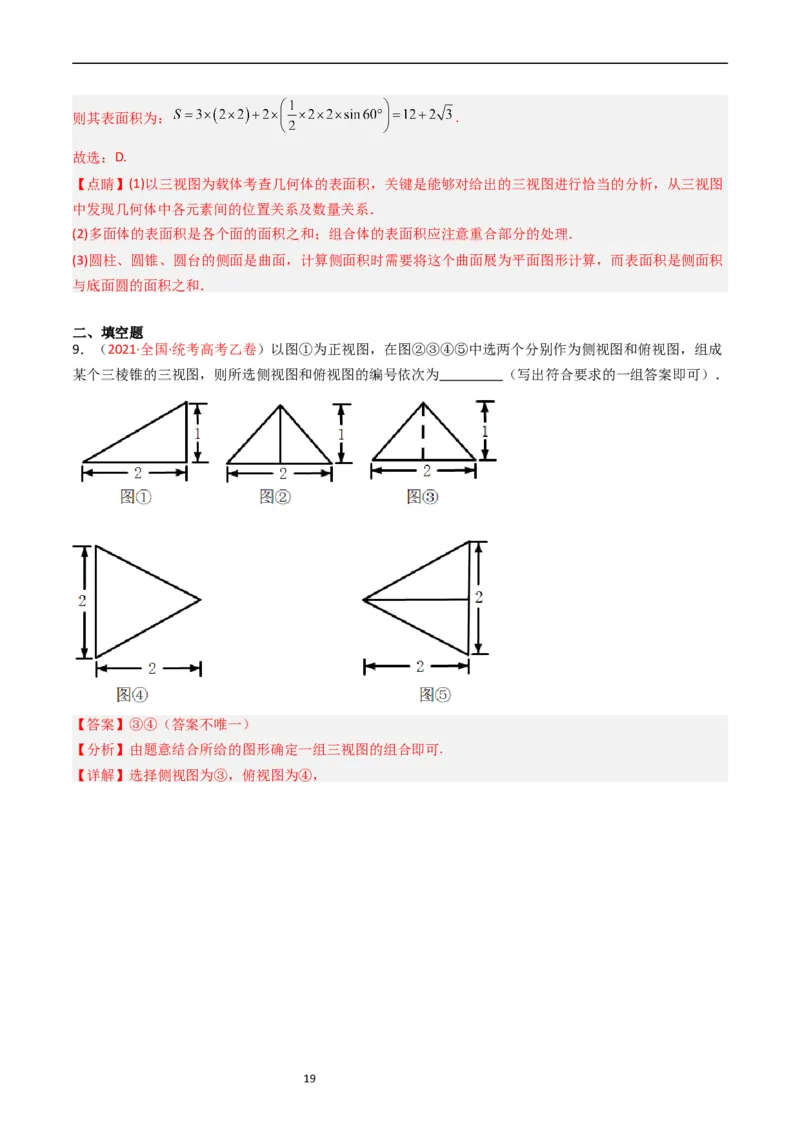
8.(2020·北京·统考高考真题)某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱的表面积为(
).
A. B. C. D.
【答案】D
【分析】首先确定几何体的结构特征,然后求解其表面积即可.
【详解】由题意可得,三棱柱的上下底面为边长为2的等边三角形,侧面为三个边长为2的正方形,
18则其表面积为: .
故选:D.
【点睛】(1)以三视图为载体考查几何体的表面积,关键是能够对给出的三视图进行恰当的分析,从三视图
中发现几何体中各元素间的位置关系及数量关系.
(2)多面体的表面积是各个面的面积之和;组合体的表面积应注意重合部分的处理.
(3)圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展为平面图形计算,而表面积是侧面积
与底面圆的面积之和.
二、填空题
9.(2021·全国·统考高考乙卷)以图①为正视图,在图②③④⑤中选两个分别作为侧视图和俯视图,组成
某个三棱锥的三视图,则所选侧视图和俯视图的编号依次为 (写出符合要求的一组答案即可).
【答案】③④(答案不唯一)
【分析】由题意结合所给的图形确定一组三视图的组合即可.
【详解】选择侧视图为③,俯视图为④,
19如图所示,长方体 中, ,
分别为棱 的中点,
则正视图①,侧视图③,俯视图④对应的几何体为三棱锥 .
故答案为:③④.
【点睛】三视图问题解决的关键之处是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关
系.
10.(2019·北京·高考真题)某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网
格纸上小正方形的边长为1,那么该几何体的体积为 .
【答案】40.
20【分析】本题首先根据三视图,还原得到几何体,根据题目给定的数据,计算几何体的体积.属于中等题.
【详解】如图所示,在棱长为4的正方体中,三视图对应的几何体为正方体去掉棱柱 之后余
下的几何体,
几何体的体积 .
考点 03 空间几何体内接球外切球问题
1.(2022·全国·统考高考乙卷)已知球O的半径为1,四棱锥的顶点为O,底面的四个顶点均在球O的球
面上,则当该四棱锥的体积最大时,其高为( )
A. B. C. D.
【答案】C
【分析】方法一:先证明当四棱锥的顶点O到底面ABCD所在小圆距离一定时,底面ABCD面积最大值为
,进而得到四棱锥体积表达式,再利用均值定理去求四棱锥体积的最大值,从而得到当该四棱锥的体积
最大时其高的值.
【详解】[方法一]:【最优解】基本不等式
设该四棱锥底面为四边形ABCD,四边形ABCD所在小圆半径为r,
设四边形ABCD对角线夹角为 ,
则
(当且仅当四边形ABCD为正方形时等号成立)
即当四棱锥的顶点O到底面ABCD所在小圆距离一定时,底面ABCD面积最大值为
21又设四棱锥的高为 ,则 ,
当且仅当 即 时等号成立.
故选:C
[方法二]:统一变量+基本不等式
由题意可知,当四棱锥为正四棱锥时,其体积最大,设底面边长为 ,底面所在圆的半径为 ,则 ,
所以该四棱锥的高 ,
(当且仅当 ,即 时,等号成立)
所以该四棱锥的体积最大时,其高 .
故选:C.
[方法三]:利用导数求最值
由题意可知,当四棱锥为正四棱锥时,其体积最大,设底面边长为 ,底面所在圆的半径为 ,则 ,
所以该四棱锥的高 , ,令 , ,设 ,则
,
, ,单调递增, , ,单调递减,
所以当 时, 最大,此时 .
故选:C.
【点评】方法一:思维严谨,利用基本不等式求最值,模型熟悉,是该题的最优解;
方法二:消元,实现变量统一,再利用基本不等式求最值;
方法三:消元,实现变量统一,利用导数求最值,是最值问题的常用解法,操作简便,是通性通法.
2.(2022·全国·统考新高考Ⅰ卷)已知正四棱锥的侧棱长为l,其各顶点都在同一球面上.若该球的体积为
22,且 ,则该正四棱锥体积的取值范围是( )
A. B. C. D.
【答案】C
【分析】设正四棱锥的高为 ,由球的截面性质列方程求出正四棱锥的底面边长与高的关系,由此确定正
四棱锥体积的取值范围.
【详解】∵球的体积为 ,所以球的半径 ,
[方法一]:导数法
设正四棱锥的底面边长为 ,高为 ,
则 , ,
所以 ,
所以正四棱锥的体积 ,
所以 ,
当 时, ,当 时, ,
所以当 时,正四棱锥的体积 取最大值,最大值为 ,
又 时, , 时, ,
所以正四棱锥的体积 的最小值为 ,
所以该正四棱锥体积的取值范围是 .
故选:C.
[方法二]:基本不等式法
由方法一故所以 当且仅当 取到 ,
23当 时,得 ,则
当 时,球心在正四棱锥高线上,此时 ,
,正四棱锥体积 ,故该正四棱锥体积的取值范围是
3.(2022·全国·统考新高考Ⅱ卷)已知正三棱台的高为1,上、下底面边长分别为 和 ,其顶点都
在同一球面上,则该球的表面积为( )
A. B. C. D.
【答案】A
【分析】根据题意可求出正三棱台上下底面所在圆面的半径 ,再根据球心距,圆面半径,以及球的半
径之间的关系,即可解出球的半径,从而得出球的表面积.
【详解】设正三棱台上下底面所在圆面的半径 ,所以 ,即 ,设球
心到上下底面的距离分别为 ,球的半径为 ,所以 , ,故 或
,即 或 ,解得 符合题意,所以球的表面积为
.
故选:A.
4.(2021·全国·统考高考甲卷)已知A,B,C是半径为1的球O的球面上的三个点,且
,则三棱锥 的体积为( )
A. B. C. D.
24【答案】A
【分析】由题可得 为等腰直角三角形,得出 外接圆的半径,则可求得 到平面 的距离,
进而求得体积.
【详解】 , 为等腰直角三角形, ,
则 外接圆的半径为 ,又球的半径为1,
设 到平面 的距离为 ,
则 ,
所以 .
故选:A.
【点睛】关键点睛:本题考查球内几何体问题,解题的关键是正确利用截面圆半径、球半径、球心到截面
距离的勾股关系求解.
5.(2020·全国·统考高考Ⅰ卷)已知 为球 的球面上的三个点,⊙ 为 的外接圆,若⊙
的面积为 , ,则球 的表面积为( )
A. B. C. D.
【答案】A
【分析】由已知可得等边 的外接圆半径,进而求出其边长,得出 的值,根据球的截面性质,求
出球的半径,即可得出结论.
【详解】设圆 半径为 ,球的半径为 ,依题意,
得 , 为等边三角形,
由正弦定理可得 ,
,根据球的截面性质 平面 ,
,
球 的表面积 .
故选:A
25【点睛】本题考查球的表面积,应用球的截面性质是解题的关键,考查计算求解能力,属于基础题.
6.(2019·全国·高考Ⅰ卷)已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为
2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为
A. B. C. D.
【答案】D
【分析】先证得 平面 ,再求得 ,从而得 为正方体一部分,进而知正
方体的体对角线即为球直径,从而得解.
【详解】解法一: 为边长为2的等边三角形, 为正三棱锥,
,又 , 分别为 、 中点,
, ,又 , 平面 , 平面 ,
, 为正方体一部分, ,即
,故选D.
解法二:
设 , 分别为 中点,
,且 , 为边长为2的等边三角形,
又
中余弦定理 ,作 于 , ,
为 中点, , ,
26, ,又 , 两两垂直,
, , ,故选D.
【点睛】本题考查学生空间想象能力,补体法解决外接球问题.可通过线面垂直定理,得到三棱两两互相
垂直关系,快速得到侧棱长,进而补体成正方体解决.
二、填空题
7.(2023·全国·统考高考甲卷)在正方体 中,E,F分别为AB, 的中点,以EF为直
径的球的球面与该正方体的棱共有 个公共点.
【答案】12
【分析】根据正方体的对称性,可知球心到各棱距离相等,故可得解.
【详解】不妨设正方体棱长为2, 中点为 ,取 , 中点 ,侧面 的中心为 ,连接
,如图,
由题意可知, 为球心,在正方体中, ,
即 ,
则球心 到 的距离为 ,
所以球 与棱 相切,球面与棱 只有1个交点,
同理,根据正方体的对称性知,其余各棱和球面也只有1个交点,
所以以EF为直径的球面与正方体每条棱的交点总数为12.
故答案为:12
8.(2019·全国·高考Ⅱ卷)中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、
正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种
或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面
体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有 个
面,其棱长为 .
27【答案】 共26个面. 棱长为 .
【分析】第一问可按题目数出来,第二问需在正方体中简单还原出物体位置,利用对称性,平面几何解决.
【详解】由图可知第一层与第三层各有9个面,计18个面,第二层共有8个面,所以该半正多面体共有
个面.
如图,设该半正多面体的棱长为 ,则 ,延长 与 交于点 ,延长 交正方体棱于 ,
由半正多面体对称性可知, 为等腰直角三角形,
,
,即该半正多面体棱长为 .
【点睛】本题立意新颖,空间想象能力要求高,物体位置还原是关键,遇到新题别慌乱,题目其实很简单,
稳中求胜是关键.立体几何平面化,无论多难都不怕,强大空间想象能力,快速还原图形.
考点 04 空间几何题的情景化应用
1.(2023·北京·统考高考真题)坡屋顶是我国传统建筑造型之一,蕴含着丰富的数学元素.安装灯带可以
勾勒出建筑轮廓,展现造型之美.如图,某坡屋顶可视为一个五面体,其中两个面是全等的等腰梯形,两
个面是全等的等腰三角形.若 ,且等腰梯形所在的平面、等腰三角形所在的平面
与平面 的夹角的正切值均为 ,则该五面体的所有棱长之和为( )
28A. B.
C. D.
【答案】C
【分析】先根据线面角的定义求得 ,从而依次求 , , , ,再把所
有棱长相加即可得解.
【详解】如图,过 做 平面 ,垂足为 ,过 分别做 , ,垂足分别为 ,
,连接 ,
由题意得等腰梯形所在的面、等腰三角形所在的面与底面夹角分别为 和 ,
所以 .
因为 平面 , 平面 ,所以 ,
因为 , 平面 , ,
所以 平面 ,因为 平面 ,所以 ,.
同理: ,又 ,故四边形 是矩形,
所以由 得 ,所以 ,所以 ,
所以在直角三角形 中,
在直角三角形 中, , ,
又因为 ,
所有棱长之和为 .
故选:C
2.(2022·全国·统考新高考Ⅱ卷)图1是中国古代建筑中的举架结构, 是桁,相邻桁的
水平距离称为步,垂直距离称为举,图2是某古代建筑屋顶截面的示意图.其中 是举,
29是相等的步,相邻桁的举步之比分别为 .已知
成公差为0.1的等差数列,且直线 的斜率为0.725,则 ( )
A.0.75 B.0.8 C.0.85 D.0.9
【答案】D
【分析】设 ,则可得关于 的方程,求出其解后可得正确的选项.
【详解】设 ,则 ,
依题意,有 ,且 ,
所以 ,故 ,
故选:D
3.(2022·天津·统考高考真题)如图,“十字歇山”是由两个直三棱柱重叠后的景象,重叠后的底面为正
方形,直三棱柱的底面是顶角为 ,腰为3的等腰三角形,则该几何体的体积为( )
A.23 B.24 C.26 D.27
【答案】D
【分析】作出几何体直观图,由题意结合几何体体积公式即可得组合体的体积.
30【详解】该几何体由直三棱柱 及直三棱柱 组成,作 于M,如图,
因为 ,所以 ,
因为重叠后的底面为正方形,所以 ,
在直棱柱 中, 平面BHC,则 ,
由 可得 平面 ,
设重叠后的EG与 交点为
则
则该几何体的体积为 .
故选:D.
4.(2021·全国·统考新高考Ⅱ卷)2020年12月8日,中国和尼泊尔联合公布珠穆朗玛峰最新高程为
8848.86(单位:m),三角高程测量法是珠峰高程测量方法之一.如图是三角高程测量法的一个示意图,
现有A,B,C三点,且A,B,C在同一水平面上的投影 满足 , .由C
点测得B点的仰角为 , 与 的差为100;由B点测得A点的仰角为 ,则A,C两点到水平面
的高度差 约为( )( )
A.346 B.373 C.446 D.473
【答案】B
31【分析】通过做辅助线,将已知所求量转化到一个三角形中,借助正弦定理,求得 ,进而得到答案.
【详解】
过 作 ,过 作 ,
故 ,
由题,易知 为等腰直角三角形,所以 .
所以 .
因为 ,所以
在 中,由正弦定理得:
,
而 ,
所以
所以 .
故选:B.
5.(2021·全国·统考高考真题)北斗三号全球卫星导航系统是我国航天事业的重要成果.在卫星导航系统
中,地球静止同步卫星的轨道位于地球赤道所在平面,轨道高度为 (轨道高度是指卫星到地球表
面的距离).将地球看作是一个球心为O,半径r为 的球,其上点A的纬度是指 与赤道平面所
成角的度数.地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为 ,记卫星信号覆盖
地球表面的表面积为 (单位: ),则S占地球表面积的百分比约为( )
A.26% B.34% C.42% D.50%
【答案】C
【分析】由题意结合所给的表面积公式和球的表面积公式整理计算即可求得最终结果.
【详解】由题意可得,S占地球表面积的百分比约为:
32.
故选:C.
6.(2020·全国·统考高考Ⅰ卷)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,
以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与
底面正方形的边长的比值为( )
A. B. C. D.
【答案】C
【分析】设 ,利用 得到关于 的方程,解方程即可得到答案.
【详解】如图,设 ,则 ,
由题意 ,即 ,化简得 ,
解得 (负值舍去).
故选:C.
【点晴】本题主要考查正四棱锥的概念及其有关计算,考查学生的数学计算能力,是一道容易题.
7.(2020·山东·统考高考真题)日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面
的影子来测定时间.把地球看成一个球(球心记为O),地球上一点A的纬度是指OA与地球赤道所在平面所
成角,点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷,若晷面与赤道所在平面平
行,点A处的纬度为北纬40°,则晷针与点A处的水平面所成角为( )
33A.20° B.40°
C.50° D.90°
【答案】B
【分析】画出过球心和晷针所确定的平面截地球和晷面的截面图,根据面面平行的性质定理和线面垂直的
定义判定有关截线的关系,根据点 处的纬度,计算出晷针与点 处的水平面所成角.
【详解】画出截面图如下图所示,其中 是赤道所在平面的截线; 是点 处的水平面的截线,依题意可
知 ; 是晷针所在直线. 是晷面的截线,依题意依题意,晷面和赤道平面平行,晷针与晷面垂直,
根据平面平行的性质定理可得可知 、根据线面垂直的定义可得 ..
由于 ,所以 ,
由于 ,
所以 ,也即晷针与点 处的水平面所成角为 .
故选:B
【点睛】本小题主要考查中国古代数学文化,考查球体有关计算,涉及平面平行,线面垂直的性质,属于
中档题.
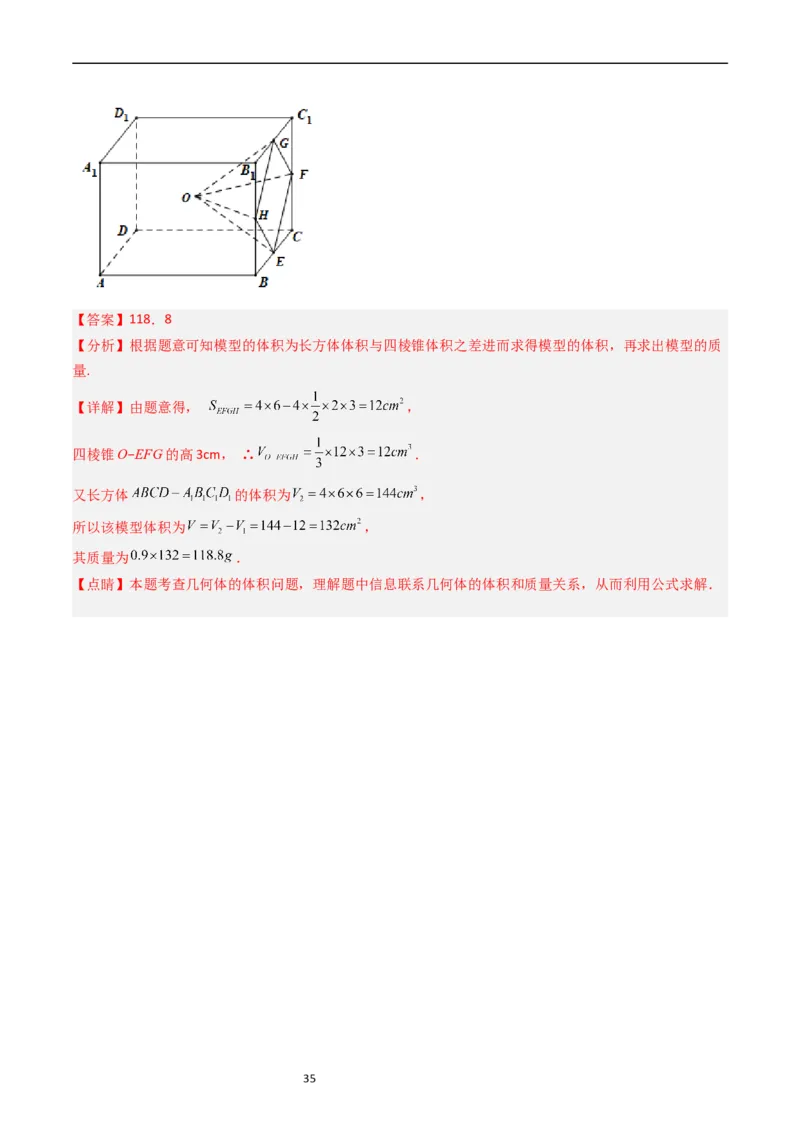
8.(2019·全国·统考高考Ⅲ卷)学生到工厂劳动实践,利用 打印技术制作模型.如图,该模型为长方体
挖去四棱锥 后所得的几何体,其中 为长方体的中心, 分别为所在
棱的中点, , 打印所用原料密度为 ,不考虑打印损耗,制作该模型
所需原料的质量为 .
34【答案】118.8
【分析】根据题意可知模型的体积为长方体体积与四棱锥体积之差进而求得模型的体积,再求出模型的质
量.
【详解】由题意得, ,
四棱锥O−EFG的高3cm, ∴ .
又长方体 的体积为 ,
所以该模型体积为 ,
其质量为 .
【点睛】本题考查几何体的体积问题,理解题中信息联系几何体的体积和质量关系,从而利用公式求解.
35