黑龙江省佳木斯高中教学联合体2023-2024学年高三上学期10月月考试题数学(1)_2023年10月_01每日更新_18号_2024届黑龙江省佳木斯高中教学联合体高三上学期10月月考

四校联考第一次调研考试高三数学试题 试卷满分：150分，考试时间：120分 注意事项： 1．答题前请粘贴好条形码，填写好自己的姓名、班级、考号等信息． 2．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分 150分． 第Ⅰ卷（选择题） 一、单选题（每小题 5分．） x3 |x1|2 1. “ ”是“ ”的（ ） A. 充分不必要条件 B. 必要不充分条件 C 充要条件 D. 既不充分又不必要条件 . 2 2. 使 1成立的一个必要不充分条件是（ ） x A. 0 x2 B. 0 x2 C. x  2 D. 0 x2 x2 1 3. 函数 f x 的大致图象为（ ） x A. B. C D. . 4. 设命题 p:x0,ex  x1，则p为（ ） A. x0,ex  x1 B. x0,ex  x1 C. x0,ex  x1 D. x0,ex  x1 5. 设集合Ax|(x2)(x4)0 ，B2,3,4,5 ，则A  B（ ） A. 2 B. 2,3 C. 3,4 D. 2,3,46. 已知函数 f(x)对任意xR都有 f(x2)f(x)，且 f(x)f(x)，当x(1,1]时， f(x) x3．则 下列结论正确的是（ ） A. 当x[2,3]时， f(x)(x2)3 B. 函数y | f(x)|的最小正周期为2 C. 函数y f(x)图像关于点(k,0)(kZ)对称 D. 函数y f(x)图像关于直线x2k(kZ)对称 f x1 7. 若函数 f 2x1 的定义域为 1,1 ，则函数y  的定义域为（ ） x1 A. 1,2 B. 0,2 C. 1,2 D. 1,2 8. 下列选项中表示同一函数的是（ ） A. f x x0与gx1 x2 B f x x与gx . x C. f x x20232 与gx x2023  x 1,x0  ,x0 D f x 与gx x . 1,x0  1,x0 二、多选题（每小题 5分，漏选每题得 2分，错选不得分．） 9. 下列说法正确的是（ ） A. 2  2,2 B. “xR ，x2 x10”的否定是“xR，x2 x10” C. “ 2x1 2”是“x1”的充分不必要条件 D. “ab”是“ac2 bc2”的必要不充分条件 10. 下列式子中正确的是（ ） 1 A. 若10lgx，则x10 B. 若log x ，则x5 25 2 C. lg(lg10)0 D. 24log 2 5 80 11. 关于函数 f(x) x x x，下列结论正确的是（ ） A. 图像关于y轴对称 B. 图像关于原点对称 C. 在 ,+ 上单调递增 D. f x 恒大于012. 若a0，b0，且ab4，则下列不等式恒成立的是（ ） 1 1 A. a2b2 8 B.  ab 4 1 1 C. ab 2 D.  1 a b 第Ⅱ卷（非选择题） 三、填空题（每小题 5分．） 13. 2log 10log 4________． 5 5 14. 在对数式blog 102a 中，实数a的取值范围是______． a3  ax,x1  15. 已知函数 f x a 是R 上的增函数，则实数a的取值范围是_____________. 4 x2,x1    2 16. 已知 f x 是定义域为R的奇函数，且 x 0时， f x x2 2x，当 x 0时， f x 的解析式为 __________. 四、解答题（17题 10分，18、19、20、21、22题各 12分．） 17. 写出计算过程． （1）log 3log 4； 2 3 1 2  1  2  2 2 （2）83  2 0   ．      4  3   18 设全集U R，A x x2 4x30 ，B{x|x2 6x80}，C {x|t  x2t1}． . （1）求AB，Að B ； U （2）若BC  B，求实数t的取值范围． 3x5,x0  19. 已知函数 f x 的解析式 f xx5,0 x1．  2x8,x1 （1）若 f a2，求a的值； （2）画出 f x 的图象，并写出函数的值域（直接写出结果即可）． 20. 已知集合A  x|4xx2 30  ，集合Bx|2m x1m ． （1）若AB，求实数m的取值范围； （2）命题 p:xA，命题q:xB，若p是q成立的充分不必要条件，求实数m的取值范围． 21. 已知函数 f(x)ax(a0且a 1)在区间 2,4 上的最大值是16． （1）求实数a的值； （2）假设函数gxlog  x2 3x2a  的值域是R，求不等式log 12t1的实数t的取值范围． 2 a b 22. 已知函数 f(x) x 过点(1,2)． x （1）判断 f(x)在区间(1,)上的单调性，并用定义证明； （2）求函数 f(x)在 2,7 上的最大值和最小值．四校联考第一次调研考试高三数学试题 试卷满分：150分，考试时间：120分 注意事项： 1．答题前请粘贴好条形码，填写好自己的姓名、班级、考号等信息． 2．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分 150分． 第Ⅰ卷（选择题） 一、单选题（每小题 5分．） x3 |x1|2 1. “ ”是“ ”的（ ） A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分又不必要条件 【答案】B 【解析】 【分析】化简绝对值不等式，即可得出结论. 【详解】由题意， 在|x1|2中，解得：1 x3 (1,3)是(,3)的真子集，充分性不成立，必要性成立， ∴“x3”是“|x1|2”的必要不充分条件 故选：B. 2 2. 使 1成立的一个必要不充分条件是（ ） x A. 0 x2 B. 0 x2 C. x  2 D. 0 x2 【答案】A 【解析】 【分析】解分式不等式，得到不等式解集为 0,2 ，结合真子集关系得到A正确. 2 2 x 2xx0 【详解】由 1得  0，等价于 ，解得0 x2，故不等式解集为 0,2 ， x x x0 2 由于 0,2 0,2 ，故0 x2是 1成立的一个必要不充分条件，满足要求， ￿ x 其他选项均不合要求，只有A选项符合， 故选：A．x2 1 3. 函数 f x 的大致图象为（ ） x A. B. C. D. 【答案】D 【解析】 【分析】利用函数的奇偶性和单调性进行判断，可得到答案. x2 1 【详解】因为 f x ， x x2 1 x2 1 所以 f x  f(x) ， x x 又因为函数 f x 定义域为  x x0  ， 所以函数 f x 为奇函数，故A选项错误， x2 1 1 又因为当x1时， f x  x ，函数单调递增，故B和C选项错误. x x 故选：D 4. 设命题 p:x0,ex  x1，则p为（ ） A. x0,ex  x1 B. x0,ex  x1 C. x0,ex  x1 D. x0,ex  x1 【答案】C 【解析】 【分析】由全称命题的否定形式判定即可. 【详解】因为命题为全称命题，则命题的否定为x0,ex  x1． 故选：C．5. 设集合Ax|(x2)(x4)0 ，B2,3,4,5 ，则A  B（ ） A. 2 B. 2,3 C. 3,4 D. 2,3,4 【答案】B 【解析】 【分析】解一元二次不等式可得A，结合交集的概念计算即可. 【详解】由题意可得(x2)(x4)02 x4，即Ax|2 x4 ， 所以A  B 2,3 . 故选：B 6. 已知函数 f(x)对任意xR都有 f(x2)f(x)，且 f(x)f(x)，当x(1,1]时， f(x) x3．则 下列结论正确的是（ ） A. 当x[2,3]时， f(x)(x2)3 B. 函数y | f(x)|的最小正周期为2 C. 函数y f(x)图像关于点(k,0)(kZ)对称 D. 函数y f(x)图像关于直线x2k(kZ)对称 【答案】B 【解析】 【分析】根据题意，由条件可得函数 f x 的周期，画出函数 f x 的图像，结合函数图像，对选项逐一判 断，即可得到结果. 【详解】因为 f x2f x ，所以 f xf x2 ，故 f x2 f x2 ， 所以 f x 的周期为4， 又 f xf x ，所以 f x f x2 ，故 f x 关于x=1对称， 又x1,1 时， f x x3，故画出 f x 的图像如下：A选项，当x2,3 时，x20,1 ，则 f xf x2x23 ，A错误； B选项，由图像可知y  f x 的最小正周期为4， 又 f x2  f x  f x ，故y  f x 的最小正周期为2，B正确． C选项，函数y  f x 的图像关于点 1,0 不中心对称，故C错误； D选项，函数y  f x 的图像不关于直线x2对称，D错误； 故选：B f x1 7. 若函数 f 2x1 的定义域为 1,1 ，则函数y  的定义域为（ ） x1 A. 1,2 B. 0,2 C. 1,2 D. 1,2 【答案】D 【解析】 【分析】根据给定条件，利用函数有意义并结合抽象函数的定义域求解作答. 【详解】由函数 f 2x1 的定义域为 1,1 ，即1 x1，得32x11， f x1 3 x11 因此由函数y  有意义，得 ，解得1 x2， x1 x10 f x1 所以函数y  的定义域为 1,2 . x1 故选：D 8. 下列选项中表示同一函数的是（ ） A. f x x0与gx1 x2 B. f x x与gx x C. f x x20232 与gx x2023  x 1,x0  ,x0 D. f x 与gx x 1,x0  1,x0 【答案】D 【解析】【分析】根据函数三要素，即定义域、对应关系、值域，三者只要有一个不相同，函数即不是同一函数， 由此一一判断各选项，即得答案. 【详解】对于A， f x x0的定义域为{x|x0)，而gx1定义域为R， 故二者不是同一函数； x2 对于B， f x x的定义域为R，与gx 的定义域为{x|x0)， x 故二者不是同一函数； 对于C， f x x20232 |x2023|与gx x2023对应关系不同， 故二者不是同一函数；  x 1,x0  ,x0  1,x0 1,x0 对于D，gx x 1,x0  与 f x 的定义域以及对应关系、值域   1,x0 1,x0 1,x0  1,x0 都相同， 故二者为同一函数， 故选：D 二、多选题（每小题 5分，漏选每题得 2分，错选不得分．） 9. 下列说法正确的是（ ） A. 2  2,2 B. “xR ，x2 x10”的否定是“xR，x2 x10” C. “ 2x1 2”是“x1”的充分不必要条件 D. “ab”是“ac2 bc2”的必要不充分条件 【答案】ACD 【解析】 【分析】根据元素和集合的关系判断A；根据全称量词命题的否定可判断B；根据充分条件以及必要条件的 判断可判断C，D. 【详解】对于A，  2,2 的元素是2,2 ，故 2  2,2 ，正确； 对于B，“xR ，x2 x10”为全称量词命题，它的否定是“xR，x2 x10”，B错误； 3 1 对于C，由 2x1 2，可得22x12,  x ，则x1成立， 2 2当x1时，比如取x2，推不出 2x1 2成立， 故“ 2x1 2”是“x1”的充分不必要条件，C正确； 对于D，当ab时，若c=0，则ac2 bc2不成立， 当ac2 bc2成立时，则c0，则c2 0，故ab， 故“ab”是“ac2 bc2”的必要不充分条件，D正确， 故选：ACD 10. 下列式子中正确的是（ ） 1 A. 若10lgx，则x10 B. 若log x ，则x5 25 2 C. lg(lg10)0 D. 24log 2 5 80 【答案】CD 【解析】 【分析】根据题意，由对数的运算性质，代入计算，即可得到结果. 【详解】若10lgx，则x1010，故A错误； 1 1 若log x ，则 ，故B错误； 25 2 x252 5 因为lg101，则lg(lg10)lg10，故C正确； 24log 2 5 242log 2 5 16580，故D正确； 故选：CD 11. 关于函数 f(x) x x x，下列结论正确的是（ ） A. 图像关于y轴对称 B. 图像关于原点对称 C. 在 ,+ 上单调递增 D. f x 恒大于0 【答案】BC 【解析】 【分析】利用函数的奇偶性，单调性，值域直接判断可得选项. 【详解】解: 函数 f(x) x x x定义域为R, f(x)x x x  x x x  f x ，函数 f x 为 奇函数，故B正确，A不正确； 当x0时， f(x) x2 x,在0,单调递增，又函数 f x 为奇函数，所以 f x 在,0上单调递增，所以函数 f x 在 ,+ 上单调递增，故C正确； 2  1 1 1 当x0时, f(x) x2 x  x+    ，故D不正确，  2 4 4 故选：BC. 12. 若a0，b0，且ab4，则下列不等式恒成立的是（ ） 1 1 A a2b2 8 B.  . ab 4 1 1 C. ab 2 D.  1 a b 【答案】AB 【解析】 【分析】根据已知条件，利用基本不等式结合不等式的性质，判断选项中的不等式是否恒成立. 【详解】16ab2 a2 2abb2 2  a2 b2 ，则a2b2 8，当且仅当ab2时取等号，A正 确； 1 1 ab42 ab ，即 ab 2，ab4，则  ，当且仅当ab2时取等号，B正确，C错误； ab 4 1 1 ab 4    1，D错误． a b ab ab 故选：AB 第Ⅱ卷（非选择题） 三、填空题（每小题 5分．） 13. 2log 10log 4________． 5 5 【答案】2 【解析】 【分析】根据对数运算法则直接求解即可. 100 【详解】2log 10log 4log 100log 4log log 252. 5 5 5 5 5 4 5 故答案为：2. 14. 在对数式blog 102a 中，实数a的取值范围是______． a3 【答案】 3,4  4,5 【解析】 【分析】根据对数的概念与性质，列出不等式组，即可求解. a30,  【详解】由题意得 a31, ,  102a0,  解得3a5且a 4， 故实数a的取值范围为 3,4  4,5 ． 故答案为： 3,4  4,5  ax,x1  15. 已知函数 f x a 是R 上的增函数，则实数a的取值范围是_____________. 4 x2,x1    2 【答案】 4,8 【解析】 【分析】根据分段函数定义，利用一次函数和指数函数单调性，限定端点处的取值列出不等式组即可解出a 的取值范围.  ax,x1  【详解】函数 f x a 是R 上的增函数， 4 x2,x1    2   a 1   a 所以 4 0 ， 2    a a 4 12      2 解得4a8. 故答案为：[4,8) 16. 已知 f x 是定义域为R的奇函数，且 x 0时， f x x2 2x，当 x 0时， f x 的解析式为 __________. 【答案】 f(x)x2 2x 【解析】 【分析】设x 0，则x0，所以 f(x) x2 2x，再利用函数奇偶性代换得到答案. 【详解】设x 0，则x0，所以 f(x) x2 2x.y f(x)是奇函数，所以 f(x)f(x)x2 2x， 因此当x 0时， f(x)x2 2x. 故答案为： f(x)x2 2x 四、解答题（17题 10分，18、19、20、21、22题各 12分．） 17. 写出计算过程． （1）log 3log 4； 2 3 1 2  1  2  2 2 （2）83  2 0   ．      4  3 【答案】（1）2 （2）5 【解析】 【分析】（1）化为同底对数即可求解；（2）应用根式的运算及指数运算性质即可. 【小问1详解】 ln3 ln4 2ln2 log 3log 4   2 2 3 ln2 ln3 ln2 【小问2详解】 1  9  2 2 2 原式 3 82   1  4 1 5   4 3 3 3     18. 设全集U R，A x x2 4x30 ，B{x|x2 6x80}，C {x|t  x2t1}． （1）求AB，Að B ； U （2）若BC  B，求实数t的取值范围． 【答案】（1）AB {x|2 x3}，A  (ð U B){x|x4或x3} 5 （2）t 1或2t  2 【解析】 【分析】（1）根据一元二次不等式的解法分别求出集合A,B，然后利用集合的基本运算即可求解； （2）由BC  B可得：C  B，然后分C 和C两种情况进行讨论即可求解. 【小问1详解】 因为A{x|x2 4x30}={x|1 x3}，集合B{x|x2 6x80}{x|2x4}，则ð B{x|x4或x≤2}， U 所以AB {x|2 x3}，A(ð B){x|x4或x3}. U 【小问2详解】 由BC  B可得C  B，因为C {x|t  x2t1}， 分C 和C两种情况， 若C 时，则有t 2t1，解得：t 1； t 2t1  5 若C时，则有t 2 ，解得：2t  ， 2  2t14  5 综上可得：实数t的取值范围为：t 1或2t  . 2 3x5,x0  19. 已知函数 f x 的解析式 f xx5,0 x1．  2x8,x1  （1）若 f a2，求a的值； （2）画出 f x 的图象，并写出函数的值域（直接写出结果即可）． 【答案】（1）1或3 （2） ,6 【解析】 【分析】(1)根据分段函数的解析式分类讨论求解； (2)根据图象求解值域. 【小问1详解】若a0, f(a)3a52解得a1， 若0a1, f(a)a52解得a3（舍）， 若a1, f(a)2a82解得a3， 综上a的值1或3. 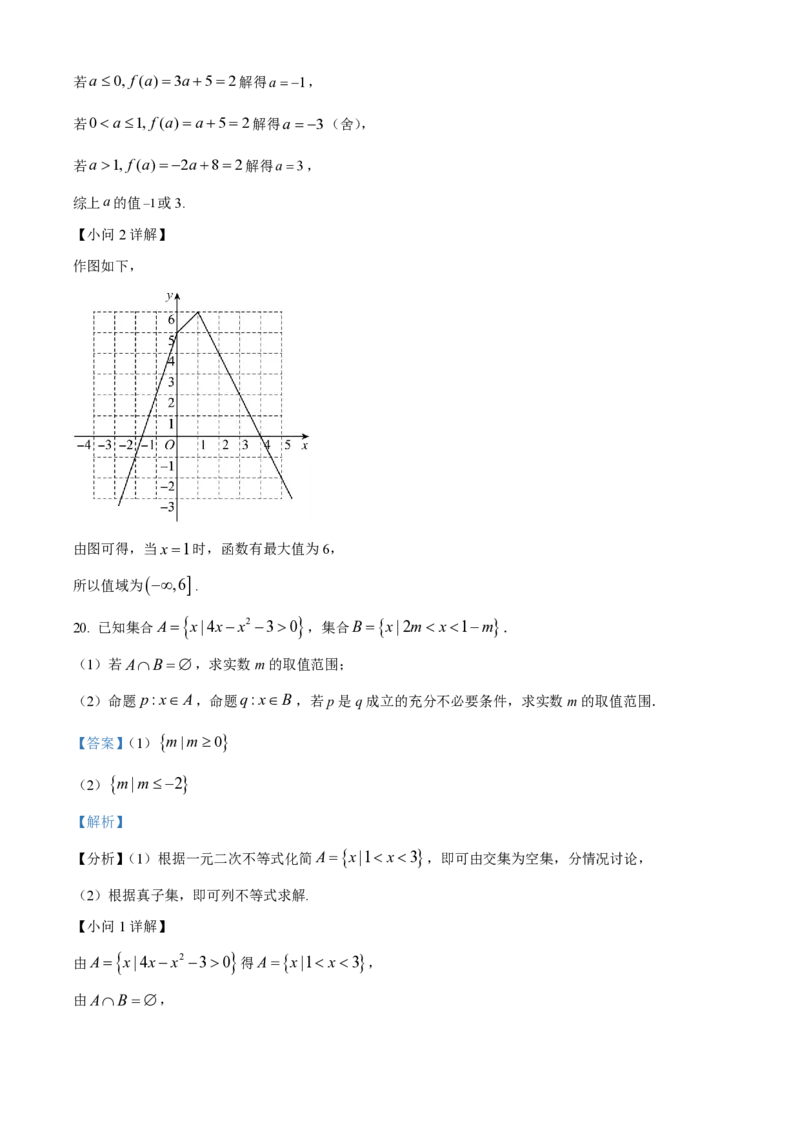【小问2详解】 作图如下， 由图可得，当x1时，函数有最大值为6， 所以值域为 ,6 . 20. 已知集合A  x|4xx2 30  ，集合Bx|2m x1m ． （1）若AB，求实数m的取值范围； （2）命题 p:xA，命题q:xB，若p是q成立的充分不必要条件，求实数m的取值范围． 【答案】（1） m|m0 （2） m|m2 【解析】 【分析】（1）根据一元二次不等式化简Ax|1 x3 ，即可由交集为空集，分情况讨论， （2）根据真子集，即可列不等式求解. 【小问1详解】 由A  x|4xx2 30  得Ax|1 x3 ， 由AB，1 ①若2m³ 1- m，即m 时，B，符合题意； 3  1  1 1 m m 1 ②若2m< 1- m，即m 时，需 3 或 3 ，解得0m ． 3 3  1m1  2m3 综上，实数m的取值范围为 m|m0 ． 【小问2详解】 1m2m  由已知A是B的真子集，知2m1 ，且两个端点不同时取等号，解得m2．  1m3  由实数m的取值范围为 m|m2 ． 21. 已知函数 f(x)ax(a0且a 1)在区间 2,4 上的最大值是16． （1）求实数a的值； （2）假设函数gxlog  x2 3x2a  的值域是R，求不等式log 12t1的实数t的取值范围． 2 a 1 【答案】（1）a  或a2 4  3 （2） ,   8 【解析】 【分析】（1）对a分类讨论，利用对数函数的单调性求出最大值，结合已知可得a的方程，即可求解a的 值； （2）由已知可得方程x2 3x2a 0的判别式0，从而可求出a的取值范围，结合（1）中结论可得 a的值，再解对数不等式即可得解． 【小问1详解】 当0a1时，函数 f(x)在区间 2,4 上是减函数， 1 因此当x2时，函数 f(x)取得最大值16，即a2 16，因此a  ， 4 当a 1时，函数 f(x)在区间 2,4 上是增函数， 当x4时，函数 f(x)取得最大值16，即a4 16，因此a2． 【小问2详解】因为gxlog  x2 3x2a  的值域是R ， 2 所以x2 3x2a可以取到所有正实数， 所以方程x2 3x2a 0的判别式0， 9 即98a 0，解得a ， 8 1 1 由因为a  或a2，所以a  ， 4 4 log 12t1 1 代入不等式得 1 ，即12t  ， 4 4 3  3 解得t  ，因此实数t的取值范围是 ,  ． 8  8 b 22. 已知函数 f(x) x 过点(1,2)． x （1）判断 f(x)在区间(1,)上的单调性，并用定义证明； （2）求函数 f(x)在 2,7 上的最大值和最小值． 【答案】（1） f(x)在区间(1,)上单调递增，证明见解析 50 5 （2）最大值为 ，最小值为 7 2 【解析】 【分析】（1）求出函数的表达式，利用单调性定义即可判断函数的单调性； （2）根据单调性即可得出函数 f(x)在 2,7 上的最大值和最小值. 【小问1详解】 单调递增，由题意证明如下， b b 由函数 f(x) x 过点(1,2)，有1 2， x 1 1 解得b1，所以 f(x)的解析式为： f(x) x ． x 设x ,x (1,)，且x  x ，有 1 2 1 2  1   1  x x x x 1 f x  f x x  x   1 2 1 2 ． 1 2 1 x 2 x x x     1 2 1 2 由x ,x (1,),x  x ，得x x 10,x x 0． 1 2 1 2 1 2 1 2x x x x 1 则 1 2 1 2 0，即 f x  f x  ． x x 1 2 1 2 ∴ f(x)在区间(1,)上单调递增． 【小问2详解】 由 f(x)在(1,)上是增函数， 5 50 所以 f(x)在区间[2,7]上的最小值为 f(2) ，最大值为 f(7) ． 2 7