文档内容
五年(2019-2023)年高考真题分项汇编
专题 07 平面解析几何(选填题)
平面解析几何在高考中考查比例较大,一般是1+1+1模式或者是2+1+1模式。在选题中,解析几何一般为
一道简单题目加上一道中等难度题目。常考题型为
考点 1 :直线和圆的综合问 题
考点 2 :椭圆 ,双曲线基本性质
考点 3:椭圆双曲线的离心率
考点 4 :抛物线 性质及应用
考点 5 :圆锥曲线的综合问题
考点 01 直线与圆的综合问题
1.(2022高考北京卷)若直线 是圆 的一条对称轴,则 ( )
A. B. C.1 D.
【答案】A
解析:由题可知圆心为 ,因为直线是圆的对称轴,所以圆心在直线上,即 ,解得
.
故选,A.
2.(2020北京高考)已知半径为 的圆经过点 ,则其圆心到原点的距离的最小值为 ( ).
A. B. C. D.
【答案】A
【解析】设圆心 ,则 ,化简得 ,
所以圆心 的轨迹是以 为圆心, 为半径的圆,
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 1所以 ,所以 ,
当且仅当 在线段 上时取得等号,故选:A.
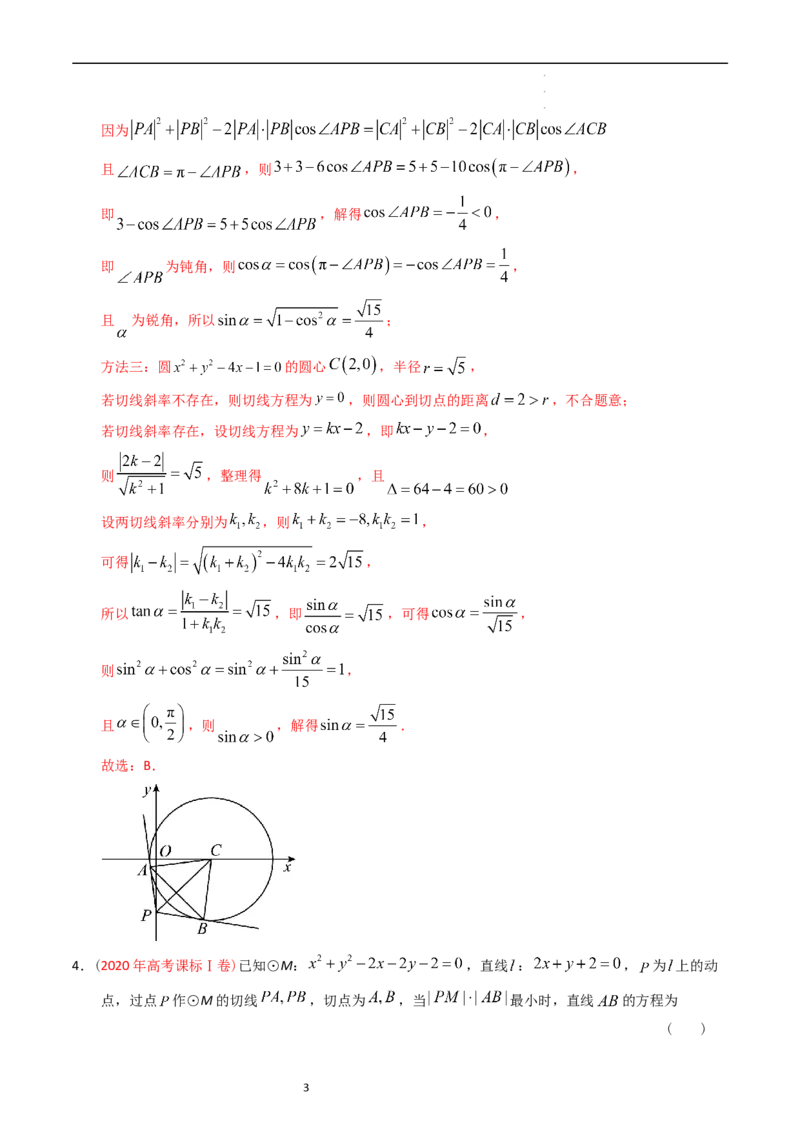
3.(2023 年新课标全国Ⅰ卷·)过点 与圆 相切的两条直线的夹角为 ,则
( )
A.1 B. C. D.
【答案】B
解析:方法一:因为 ,即 ,可得圆心 ,半径 ,
过点 作圆C的切线,切点为 ,
因为 ,则 ,
可得 ,
则 ,
,
即 为钝角,
所以 ;
法二:圆 的圆心 ,半径 ,
过点 作圆C的切线,切点为 ,连接 ,
可得 ,则 ,
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 2因为
且 ,则 ,
即 ,解得 ,
即 为钝角,则 ,
且 为锐角,所以 ;
方法三:圆 的圆心 ,半径 ,
若切线斜率不存在,则切线方程为 ,则圆心到切点的距离 ,不合题意;
若切线斜率存在,设切线方程为 ,即 ,
则 ,整理得 ,且
设两切线斜率分别为 ,则 ,
可得 ,
所以 ,即 ,可得 ,
则 ,
且 ,则 ,解得 .
故选:B.
4.(2020年高考课标Ⅰ卷)已知⊙M: ,直线 : , 为 上的动
点,过点 作⊙M的切线 ,切点为 ,当 最小时,直线 的方程为
( )
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 3A. B. C. D.
【答案】D
【解析】圆的方程可化为 ,点 到直线 的距离为 ,
所以直线 与圆相离.
依圆的知识可知,四点 四点共圆,且 ,所以
,而 ,
当直线 时, , ,此时 最小.
∴ 即 ,由 解得, .
所以以 为直径的圆的方程为 ,即 ,
两圆的方程相减可得: ,即为直线 的方程.
故选:D.
【点睛】本题主要考查直线与圆,圆与圆的位置关系的应用,以及圆的几何性质的应用,意在考查学
生的转化能力和数学运算能力,属于中档题.
5.(2020年高考课标Ⅱ卷)若过点(2,1)的圆与两坐标轴都相切,则圆心到直线 的距离为
( )
A. B. C. D.
【答案】B
解析:由于圆上的点 在第一象限,若圆心不在第一象限,
则圆与至少与一条坐标轴相交,不合乎题意,所以圆心必在第一象限,
设圆心的坐标为 ,则圆的半径为 ,
圆的标准方程为 .
由题意可得 ,
可得 ,解得 或 ,
所以圆心的坐标为 或 ,
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 4圆心 到直线 的距离均为 ;
圆心 到直线 的距离均为
圆心到直线 的距离均为 ;
所以,圆心到直线 的距离为 .
故选:B.
【点睛】本题考查圆心到直线距离的计算,求出圆的方程是解题的关键,考查计算能力,属于中等题.
6.(2021高考北京)已知直线 ( 为常数)与圆 交于点 ,当 变化时,若
的最小值为2,则 ( )
A. B. C. D.
【答案】C
解析:由题可得圆心为 ,半径为2, 则圆心到直线的距离 ,
则弦长为 ,
则当 时,弦长 取得最小值为 ,解得 .
故选:C.
二 填空题
1.(2020北京高考)为满足人民对美好生活的向往,环保部门要求相关企业加强污水治理,排放未达标的
企业要限期整改、设企业的污水摔放量 与时间 的关系为 ,用 的大小评价在
这段时间内企业污水治理能力的强弱,已知整改期内,甲、乙两企业的污水排放量与时间的关系
如下图所示.
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 5给出下列四个结论:
①在 这段时间内,甲企业的污水治理能力比乙企业强;
②在 时刻,甲企业的污水治理能力比乙企业强;
③在 时刻,甲、乙两企业的污水排放都已达标;
④甲企业在 这三段时间中,在 的污水治理能力最强.
其中所有正确结论的序号是____________________.
【答案】①②③
【解析】 表示区间端点连线斜率的负数,
在 这段时间内,甲的斜率比乙的小,所以甲的斜率的相反数比乙的大,因此甲企业的污水治理能
力比乙企业强;①正确;
甲企业在 这三段时间中,甲企业在 这段时间内,甲的斜率最小,其相反数最大,
即在 的污水治理能力最强.④错误;
在 时刻,甲切线的斜率比乙的小,所以甲切线的斜率的相反数比乙的大,甲企业的污水治理能力比
乙企业强;②正确;
在 时刻,甲、乙两企业的污水排放量都在污水打标排放量以下,所以都已达标;③正确;故答案为:
①②③
2.(2022新高考全国I卷)写出与圆 和 都相切的一条直线的方程
________________.
【答案】 或 或
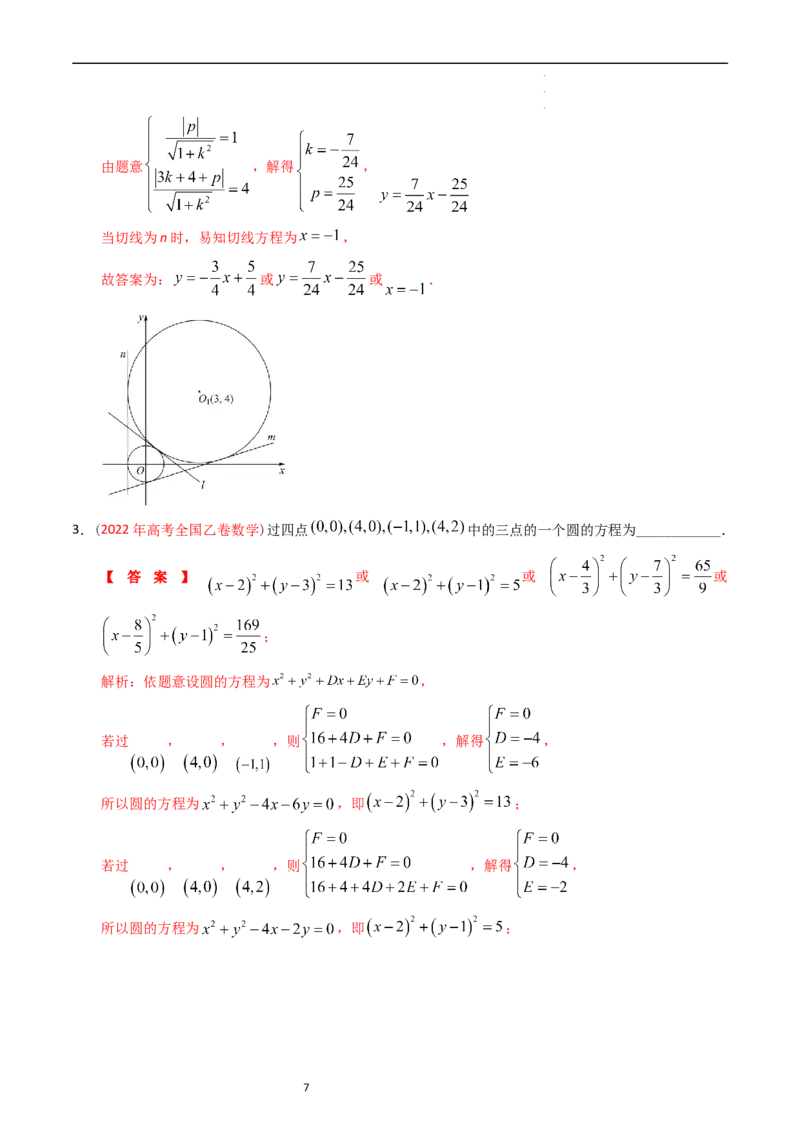
解析:圆 的圆心为 ,半径为 ,圆 的圆心 为 ,半
径为 ,
两圆圆心距为 ,等于两圆半径之和,故两圆外切,
如图,
当切线为l时,因为 ,所以 ,设方程为
O到l的距离 ,解得 ,所以l的方程为 ,
当切线为m时,设直线方程为 ,其中 , ,
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 6由题意 ,解得 ,
当切线为n时,易知切线方程为 ,
故答案为: 或 或 .
3.(2022年高考全国乙卷数学)过四点 中的三点的一个圆的方程为____________.
【 答 案 】 或 或 或
;
解析:依题意设圆的方程为 ,
若过 , , ,则 ,解得 ,
所以圆的方程为 ,即 ;
若过 , , ,则 ,解得 ,
所以圆的方程为 ,即 ;
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 7若过 , , ,则 ,解得 ,
所以圆的方程为 ,即 ;
若过 , , ,则 ,解得 ,
所以圆的方程为 ,即 ;
故答案为: 或 或 或
;
4.(2020江苏高考)在平面直角坐标系 中,已知 , , 是圆 上的两个
动点,满足 ,则 面积的最大值是__________.
【答案】
【解析】
设圆心 到直线 距离为 ,则
所以
令 (负值舍去)
当 时, ;当 时, ,因此当 时, 取最大值,即 取最大值为
,
故答案为:
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 85.(2020年浙江省高考数学试卷)设直线 ,圆 , ,
若直线 与 , 都相切,则 _______;b=______.
【答案】(1). (2).
解析:由题意, 到直线的距离等于半径,即 , ,
所以 ,所以 (舍)或者 ,
解得 .
6.(2022年高考全国甲卷数学(理))若双曲线 的渐近线与圆 相切,则
_________.
【答案】
【解析】双曲线 的渐近线为 ,即 ,
不妨取 ,圆 ,即 ,所以圆心为 ,半径 ,
依题意圆心 到渐近线 的距离 ,
解得 或 (舍去).
故答案为: .
7.(2022新高考全国II卷·第15题)设点 ,若直线 关于 对称的直线与圆
有公共点,则a的取值范围是________.
【答案】
解析: 关于 对称的点的坐标为 , 在直线 上,
所以 所在直线即为直线 ,所以直线 为 ,即 ;
圆 ,圆心 ,半径 ,
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 9依题意圆心到直线 的距离 ,
即 ,解得 ,即 ;
故答案为:
8.(2021高考天津·第12题)若斜率为 的直线与 轴交于点 ,与圆 相切于点 ,
则 ____________.
【答案】
解析:设直线 的方程为 ,则点 ,
由于直线 与圆 相切,且圆心为 ,半径为 ,
则 ,解得 或 ,所以 ,因为 ,故 .
故答案为: .
9.(2020天津高考·第12题)已知直线 和圆 相交于 两点.若 ,
则 的值为_________.
【答案】5
【解析】因为圆心 到直线 的距离 ,
由 可得 ,解得 .故答案为: .
10.(2023年新课标全国Ⅱ卷·第15题)已知直线 与 交于A,B两
点,写出满足“ 面积为 ”的m的一个值______.
【答案】 ( 中任意一个皆可以)
解析:设点 到直线 的距离为 ,由弦长公式得 ,
所以 ,解得: 或 ,
由 ,所以 或 ,解得: 或 .
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 10故答案为: ( 中任意一个皆可以).
考点 02 椭圆双曲线的基本性质
1.(2023年新课标全国Ⅱ卷·第5题)已知椭圆 的左、右焦点分别为 , ,直线
与C交于A.B两点,若 面积是 面积的2倍,则
( ).
A. B. C. D.
【答案】C
解析:将直线 与椭圆联立 ,消去 可得 ,
因为直线与椭圆相交于 点,则 ,解得 ,
设 到 的距离 到 距离 ,易知 ,
则 , ,
,解得 或 (舍去),
故选:C.
2.(2023年全国甲卷理科·第12题)设O为坐标原点, 为椭圆 的两个焦点,点P在
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 11C上, ,则 ( )
A. B. C. D.
【答案】B
解析:方法一:设 ,所以 ,
由 ,解得: ,
由椭圆方程可知, ,
所以, ,解得: ,
即 ,因此 .
故选:B.
方法二:因为 ①, ,
即 ②,联立①②,
解得: ,
而 ,所以 ,
即 .
故选:B.
方法三:因为 ①, ,
即 ②,联立①②,解得: ,
由 中 线 定 理 可 知 , , 易 知 , 解 得 :
.
故选:B.
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 123.(2021年新高考Ⅰ卷·第5题)已知 , 是椭圆 : 的两个焦点,点 在 上,则
的最大值为 ( )
A.13 B.12 C.9 D.6
【答案】C
解析:由题, ,则 ,
所以 (当且仅当 时,等号成立).
故选:C.
4 (2022年高考全国甲卷数学(理)·第10题)椭圆 的左顶点为A.点P,Q均在C上,
且关于y轴对称.若直线 的斜率之积为 ,则C的离心率为 ( )
A. B. C. D.
【答案】A
【解析】 ,设 ,则 ,
则 ,故 ,
又 ,则 ,所以 ,即 ,
所以椭圆 的离心率 .
故选:A.
5.(2019·全国Ⅰ·理·第10题)已知椭圆 的焦点为 , ,过 的直线与 交于 ,
两点.若 ,
,则 的方程为 ( )
A. B. C. D.
【答案】答案:B
解析:如图,设 ,则 ,由 ,可得
, ,所以点 为椭圆的上顶点或下顶点.
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 13在 中,由余弦定理可得 ,
所以 ,即 ,即 ,又 ,所以椭圆方程为
.
B
F1 O F2
A
6.(2023年全国乙卷理科·第11题)设A.B为双曲线 上两点,下列四个点中,可为线段AB中
点的是 ( )
A. B. C. D.
【答案】D
解析:设 ,则 的中点 ,
可得 ,
因为 在双曲线上,则 ,两式相减得 ,
所以 .
对于选项A: 可得 ,则 ,
联立方程 ,消去y得 ,
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 14此时 ,
所以直线AB与双曲线没有交点,故A错误;
对于选项B:可得 ,则 ,
联立方程 ,消去y得 ,
此时 ,
所以直线AB与双曲线没有交点,故B错误;
对于选项C:可得 ,则
由双曲线方程可得 ,则 为双曲线的渐近线,
所以直线AB与双曲线没有交点,故C错误;
对于选项D: ,则 ,
联立方程 ,消去y得 ,
此时 ,故直线AB与双曲线有交两个交点,故D正确;
故选:D.
7 (2020年高考课标Ⅲ卷理科·第11题)设双曲线C: (a>0,b>0) 左、右焦点分别为F ,
的1
F ,离心率为 .P是C上一点,且F P⊥F P.若△PF F 的面积为4,则a=
2 1 2 1 2
( )
A.1 B.2 C.4 D.8
【答案】A
解析: , ,根据双曲线的定义可得 ,
,即 ,
, ,
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 15,即 ,解得 ,
故选:A.
【点睛】本题主要考查了双曲线的性质以及定义的应用,涉及了勾股定理,三角形面积公式的应用,
属于中档题.
8.(2020年浙江省高考数学试卷·第8题)已知点O(0,0),A(–2,0),B(2,0).设点P满足|PA.–|
PB.=2,且P为函数y= 图像上的点,则|OP|= ( )
A. B. C. D.
【答案】D
解析:因为 ,所以点 在以 为焦点,实轴长为 ,焦距为 的双曲线的右支
上,由 可得, ,即双曲线的右支方程为 ,而点 还
在函数 的图象上,所以,
由 ,解得 ,即 . 故选:D.
9 (2021高考北京·第5题)若双曲线 离心率为 ,过点 ,则该双曲线的方程为
( )
A. B. C. D.
【答案】B
解析: ,则 , ,则双曲线的方程为 ,
将点 的坐标代入双曲线的方程可得 ,解得 ,故 ,
因此,双曲线的方程为 . 故选:B
10.(2020天津高考·第7题)设双曲线 的方程为 ,过抛物线 的焦点和点
的直线为 .若 的一条渐近线与 平行,另一条渐近线与 垂直,则双曲线 的方程为
( )
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 16A. B. C. D.
【答案】D
【解析】由题可知,抛物线的焦点为 ,所以直线 的方程为 ,即直线的斜率为 ,
又双曲线的渐近线的方程为 ,所以 , ,因为 ,解得 .
故选: .
11.(2019·浙江·第2题)渐近线方程为 的双曲线的离心率是 ( )
A. B. C. D.
【答案】C
【解析】由题意得 ,则双曲线是等轴双曲线,离心率 .故选C.
12.(2019·全国Ⅲ·理·第10题)双曲线C: =1的右焦点为F,点P在C的一条渐近线上,O为
坐标原点,若 ,则△PFO的面积为 ( )
A. B. C. D.
【答案】A
【解析】由 ,
又P在C的一条渐近线上,不妨设为在 上,则 .
,故选A.
【点评】本题考查以双曲线为载体的三角形面积的求法,渗透了直观想象、逻辑推理和数学运算素养.
采取公式法,利用数形结合、转化与化归和方程思想解题.
二 填空题
1.(2021年高考全国甲卷理科·第15题)已知 为椭圆C: 的两个焦点,P,Q为C上关
于坐标原点对称的两点,且 ,则四边形 的面积为________.
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 17【答案】
解析:因为 为 上关于坐标原点对称的两点,
且 ,所以四边形 为矩形,
设 ,则 ,
所以 ,
,即四边形 面积等于 .
故答案: .
2.(2022新高考全国II卷·第16题)已知直线l与椭圆 在第一象限交于A,B两点,l与x轴,y
轴分别交于M,N两点,且 ,则l的方程为___________.
【答案】
解析:令 的中点为 ,因为 ,所以 ,
设 , ,则 , ,
所以 ,即
所以 ,即 ,设直线 , , ,
令 得 ,令 得 ,即 , ,所以 ,
即 ,解得 或 (舍去),
又 ,即 ,解得 或 (舍去),
所以直线 ,即 ;
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 18故答案为:
3.(2022新高考全国I卷·第16题)已知椭圆 ,C的上顶点为A,两个焦点为 ,
,离心率为 .过 且垂直于 的直线与C交于D,E两点, ,则 的周长是
________________.
【答案】13
解析:∵椭圆的离心率为 ,∴ ,∴ ,∴椭圆的方程为
,不妨设左焦点为 ,右焦点为 ,如图所示,∵
,∴ ,∴ 为正三角形,∵过 且垂直于 的直线
与C交于D,E两点, 为线段 的垂直平分线,∴直线 的斜率为 ,斜率倒数为 ,
直 线 的 方 程 : , 代 入 椭 圆 方 程 , 整 理 化 简 得 到 :
,
判别式 ,
∴ ,
∴ , 得 ,
∵ 为线段 的垂直平分线,根据对称性, ,∴ 的周长等于
的周长,利用椭圆的定义得到 周长为
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 19故答案
为:13.
4.(2019·全国Ⅲ·理·第15题)设 为椭圆 的两个焦点, 为 上一点且在第一
象限.若 为等腰三角形,则 的坐标为___________.
【答案】
【解析】由已知可得 , .
.
设点 的坐标为 ,则 ,
又 ,解得 ,
,解得 ( 舍去),
的坐标为 .
法二、在得出 . .
,∴ .
∴ ,
的坐标为 .
法三、由题知 ,又由焦半径公式 ,得 ,
从而得到 , 的坐标为 .
【点评】本题考查椭圆标准方程及其简单性质,考查数形结合思想、转化与化归的能力,很好的落实
了直观想象、逻辑推理等数学素养.
5.(2023年北京卷·第12题)已知双曲线C的焦点为 和 ,离心率为 ,则C的方程为
____________.
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 20【答案】
解析:令双曲线 的实半轴、虚半轴长分别为 ,显然双曲线 的中心为原点,焦点在x轴上,其
半焦距 ,
由双曲线 的离心率为 ,得 ,解得 ,则 ,
所以双曲线 的方程为 .
故答案为:
6.(2023年新课标全国Ⅰ卷·第16题)已知双曲线 的左、右焦点分别为 .
点 在 上,点 在 轴上, ,则 的离心率为________.
【答案】
解析:方法一:
依题意,设 ,则 ,
在 中, ,则 ,故 或 (舍去),
所以 , ,则 ,
故 ,
所以在 中, ,整理得 ,
故 .
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 21方法二:
依题意,得 ,令 ,
因为 ,所以 ,则 ,
又 ,所以 ,则 ,
又点 在 上,则 ,整理得 ,则 ,
所以 ,即 ,
整理得 ,则 ,解得 或 ,
又 ,所以 或 (舍去),故 .
故答案为: .
7.(2021年新高考全国Ⅱ卷·第13题)已知双曲线 的离心率为2,则该双曲线的渐
近线方程为_______________
【答案】
解析:因为双曲线 的离心率为2,所以 ,所以 ,
所以该双曲线的渐近线方程为 .故答案为 .
8.(2021年高考全国乙卷理科·第13题)已知双曲线 的一条渐近线为
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 22,则C的焦距为_________.
【答案】4
解析:由渐近线方程 化简得 ,即 ,同时平方得 ,又双曲线中
,故 ,解得 (舍去), ,故焦距
故答案为:4
【点睛】本题为基础题,考查由渐近线求解双曲线中参数,焦距,正确计算并联立关系式求解是关键
9.(2020年高考课标Ⅰ卷理科·第15题)已知F为双曲线 的右焦点,A为C的右
顶点,B为C上的点,且BF垂直于x轴.若AB的斜率为3,则C的离心率为______________.
【答案】2
【解析】联立 ,解得 ,所以 .
依题可得, , ,即 ,变形得 , ,
因此,双曲线 的离心率为 .
故答案为: .
【点睛】本题主要考查双曲线的离心率的求法,以及双曲线的几何性质的应用,属于基础题.
10.(2022高考北京卷·第12题)已知双曲线 的渐近线方程为 ,则 __________.
【答案】
解析:对于双曲线 ,所以 ,即双曲线的标准方程为 ,
则 , ,又双曲线 的渐近线方程为 ,
所以 ,即 ,解得 ;故答案为:
考点 03 椭圆双曲线的离心率
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 231.(2023年新课标全国Ⅰ卷·第5题)设椭圆 的离心率分别为
.若 ,则 ( )
A. B. C. D.
【答案】A
解析:由 ,得 ,因此 ,而 ,所以 .
故选:A
2.(2021年高考全国乙卷理科·第11题)设 是椭圆 的上顶点,若 上的任意
一点 都满足 ,则 的离心率的取值范围是 ( )
A B C D
A. B. C. D.
1 1 1 1
【答案】C
解析:设 ,由 ,因为 , ,所以
,
因为 ,当 ,即 时, ,即 ,符合题意,由
可得 ,即 ;
当 ,即 时, ,即 ,化简得,
,显然该不等式不成立.
故选:C.
【点睛】本题解题关键是如何求出 的最大值,利用二次函数求指定区间上的最值,要根据定义域
讨论函数的单调性从而确定最值.
6.
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 243.(2019·全国Ⅱ·理·第8题)若抛物线 的焦点是椭圆 的一个焦点,则
( )
A. B. C. D.
【答案】D
x2 y2
【解析】因为抛物线 的焦点 是椭圆 1的一个焦点,所以
3p p
,解得 ,故选D.
p 8
【点评】利用抛物线与椭圆有共同的焦点即可列出关于 的方程,即可解出 ,或者利用检验排除的
方法,如 时,抛物线焦点为 ,椭圆焦点为 ,排除A,同样可排除B,C,故选D.
4.(2019·北京·理·第4题)已知椭圆 (a>b>0)的离心率为 ,则 ( )
A. B. C. D.
【答案】B
【解析】椭圆的离心率 ,化简得 ,故选B.
5.(2023年天津卷·第9题)双曲线 的左、右焦点分别为 .过 作其中一条
渐近线的垂线,垂足为 .已知 ,直线 的斜率为 ,则双曲线的方程为 ( )
A. B.
C. D.
【答案】D
解析:如图,
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 25因为 ,不妨设渐近线方程为 ,即 ,
所以 ,
所以 .
设 ,则 ,所以 ,所以 .
因 ,所以 ,所以 ,所以 ,
为
所以 ,
因为 ,
所以 ,
所以 ,解得 ,
所以双曲线的方程为
故选:D
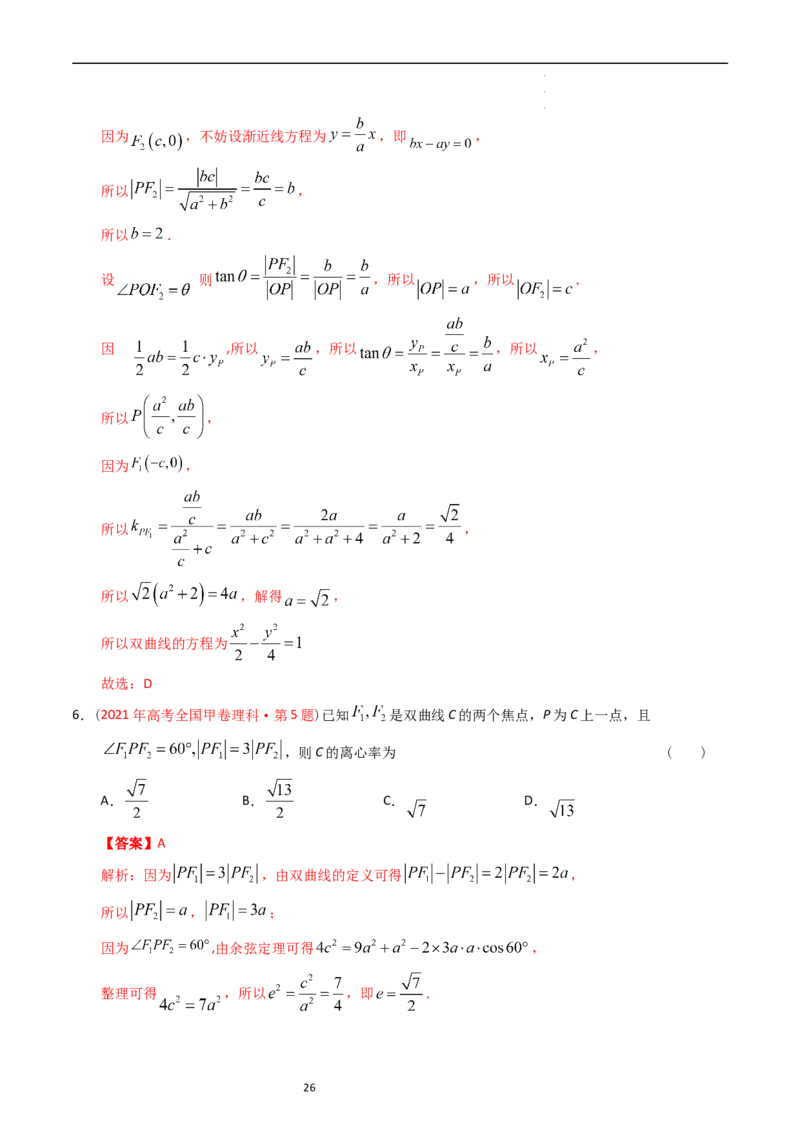
6.(2021年高考全国甲卷理科·第5题)已知 是双曲线C的两个焦点,P为C上一点,且
,则C的离心率为 ( )
A. B. C. D.
【答案】A
解析:因为 ,由双曲线的定义可得 ,
所以 , ;
因为 ,由余弦定理可得 ,
整理可得 ,所以 ,即 .
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 26故选:A
【点睛】关键点睛:双曲线的定义是入手点,利用余弦定理建立 间的等量关系是求解的关键.
7.(2020年高考课标Ⅱ卷理科·第8题)设 为坐标原点,直线 与双曲线
的两条渐近线分别交于 两点,若 的面积为8,则 的焦距的最小值为 ( )
A.4 B.8 C.16 D.32
【答案】B
解析:
双曲线的渐近线方程是
直线 与双曲线 的两条渐近线分别交于 , 两点
不妨设 为在第一象限, 在第四象限
联立 ,解得
故
联立 ,解得
故
面积为:
双曲线
其焦距为
当且仅当 取等号
的焦距的最小值:
故选:B.
【点睛】本题主要考查了求双曲线焦距的最值问题,解题关键是掌握双曲线渐近线的定义和均值不等
式求最值方法,在使用均值不等式求最值时,要检验等号是否成立,考查了分析能力和计算能力,属
于中档题.
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 278.(2022年高考全国乙卷数学(理)·第11题)双曲线C的两个焦点为 ,以C的实轴为直径的圆记为
D.过 作D的切线与C交于M,N两点,且 ,则C的离心率为
( )
A. B. C. D.
【答案】C
解析:依题意不妨设双曲线焦点在 轴,设过 作圆 的切线切点为 ,
若 分别在左右支,
因为 ,且 ,所以 在双曲线的右支,
又 , , ,
设 , ,
在 中,有 ,
故 即 ,
所以 ,
而 , , ,故 ,
代入整理得到 ,即 ,
所以双曲线的离心率
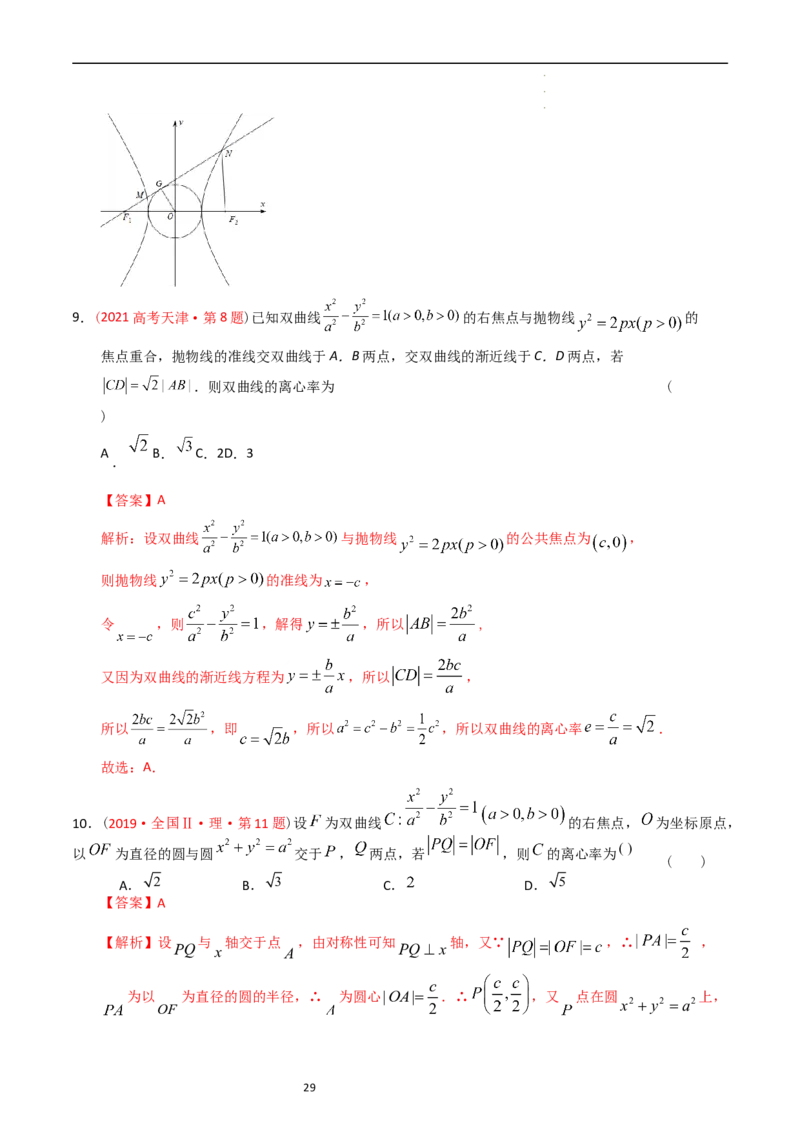
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 289.(2021高考天津·第8题)已知双曲线 的右焦点与抛物线 的
焦点重合,抛物线的准线交双曲线于A.B两点,交双曲线的渐近线于C.D两点,若
.则双曲线的离心率为 (
)
.
A B. C.2D.3
.
【答案】A
解析:设双曲线 与抛物线 的公共焦点为 ,
则抛物线 的准线为 ,
令 ,则 ,解得 ,所以 ,
又因为双曲线的渐近线方程为 ,所以 ,
所以 ,即 ,所以 ,所以双曲线的离心率 .
故选:A.
10.(2019·全国Ⅱ·理·第11题)设 为双曲线 的右焦点, 为坐标原点,
( )
以 为直径的圆与圆 交于 , 两点,若 ,则 的离心率为
( )
A. 2 B. 3 C. D. 5
【答案】A
【解析】设 与 轴交于点 ,由对称性可知 轴,又∵ ,∴ ,
PQ x A PQ x
c
为以 为直径的圆的半径,∴ 为圆心|OA| .∴ ,又 点在圆 上,
OF 2 x2 y2 a2
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 29∴ ,即 ,∴ ,∴ ,故选A.
二 填空题
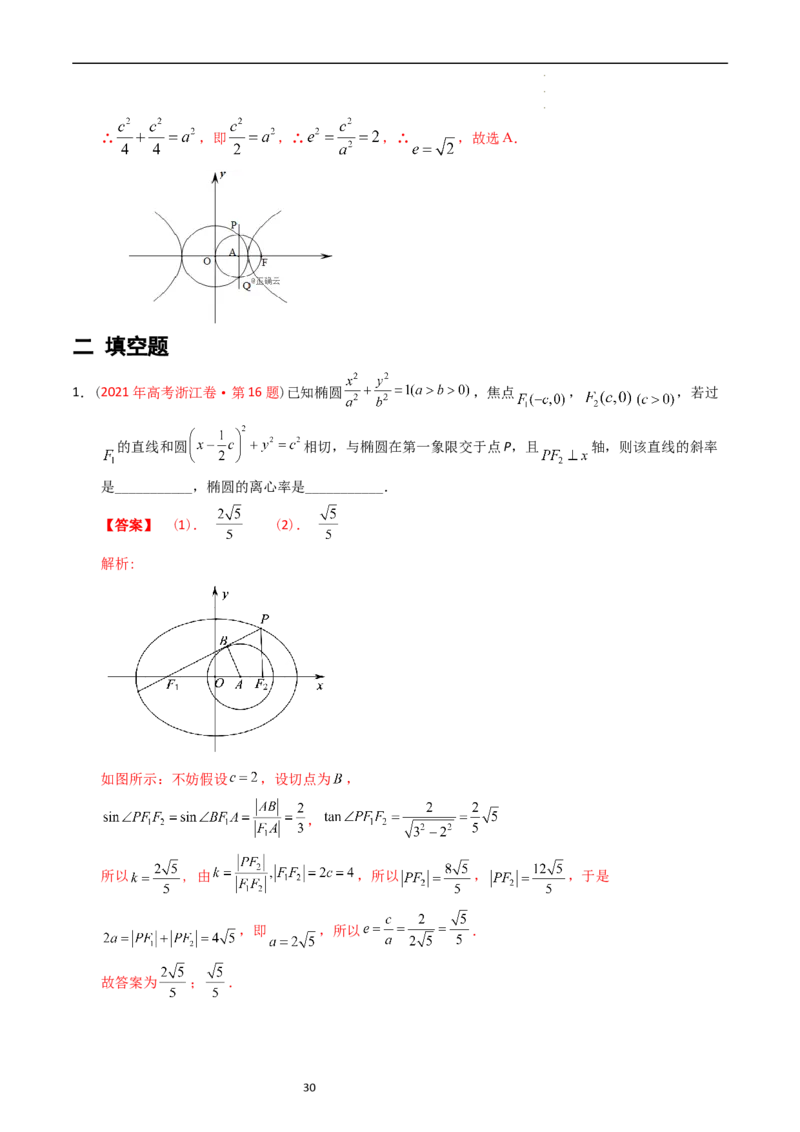
1.(2021年高考浙江卷·第16题)已知椭圆 ,焦点 , ,若过
的直线和圆 相切,与椭圆在第一象限交于点P,且 轴,则该直线的斜率
是___________,椭圆的离心率是___________.
【答案】 (1). (2).
解析:
如图所示:不妨假设 ,设切点为 ,
,
所以 , 由 ,所以 , ,于是
,即 ,所以 .
故答案为 ; .
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 302.(2022年浙江省高考数学试题·第16题)已知双曲线 的左焦点为F,过F且斜率
为 的直线交双曲线于点 ,交双曲线的渐近线于点 且 .若
,则双曲线的离心率是_________.
【答案】
解析:过 且斜率为 的直线 ,渐近线 ,
联立 ,得 ,由 ,得
而点 在双曲线上,于是 ,解得: ,所以离心率 .
故答案为: .
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 313.(2020北京高考·第12题)已知双曲线 ,则 的右焦点的坐标为_________; 的焦点到
其渐近线的距离是_________.
【答案】(1). (2).
【解析】在双曲线 中, , ,则 ,则双曲线 的右焦点坐标为 ,
双曲线 的渐近线方程为 ,即 ,
所以,双曲线 的焦点到其渐近线的距离为 .故答案为: ; .
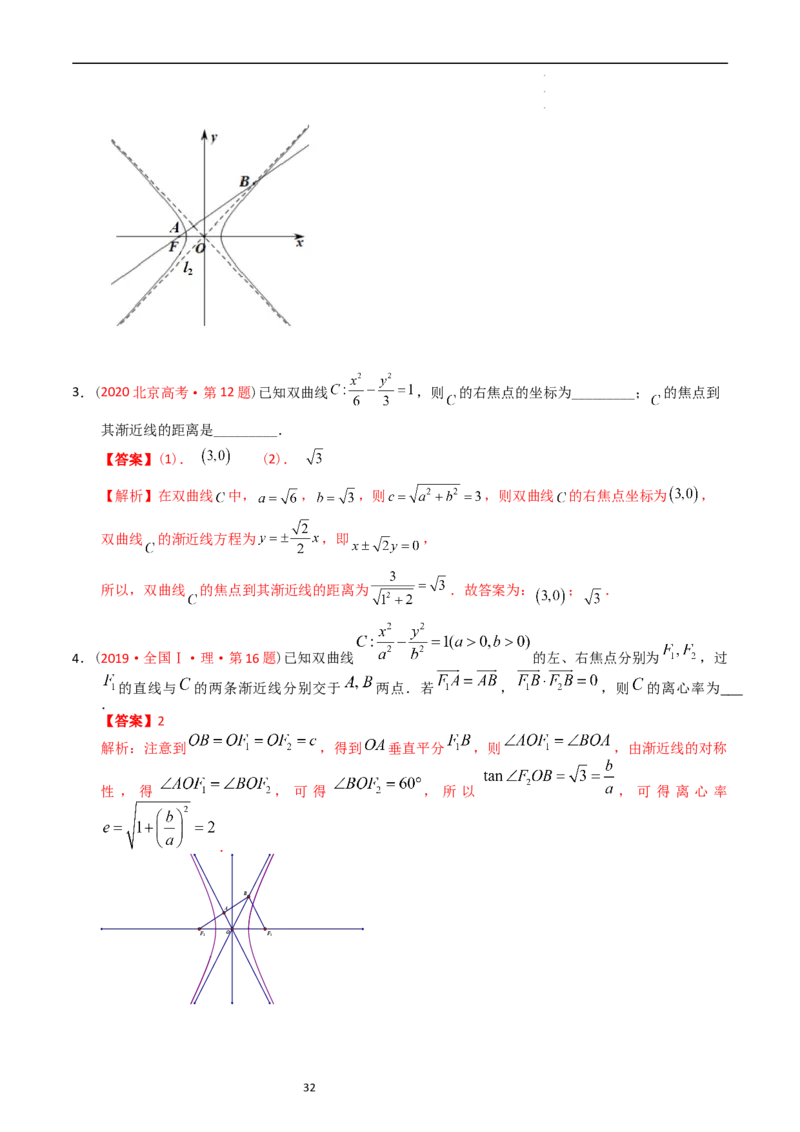
4.(2019·全国Ⅰ·理·第16题)已知双曲线 的左、右焦点分别为 ,过
的直线与 的两条渐近线分别交于 两点.若 , ,则 的离心率为
.
【答案】2
解析:注意到 ,得到 垂直平分 ,则 ,由渐近线的对称
性 , 得 , 可 得 , 所 以 , 可 得 离 心 率
.
B
A
F1 O F2
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 32考点 04 抛物线的性质及应用
1.(2023年北京卷·第6题)已知抛物线 的焦点为 ,点 在 上.若 到直线 的距
离为5,则 ( )
A.7 B.6 C.5 D.4
【答案】D
解析:因为抛物线 的焦点 ,准线方程为 ,点 在 上,
所以 到准线 的距离为 ,
又 到直线 的距离为 ,
所以 ,故 .
故选:D.
2.(2021年新高考全国Ⅱ卷·第3题)抛物线 的焦点到直线 的距离为 ,则
( )
A.1 B.2 C. D.4
【答案】B
解析:抛物线的焦点坐标为 ,其到直线 的距离: ,解得: (
舍去),故选B.
3.(2020年高考课标Ⅰ卷理科·第4题)已知A为抛物线C:y2=2px(p>0)上一点,点A到C的焦点的距离为
12,到y轴的距离为9,则p= ( )
A.2 B.3 C.6 D.9
【答案】C
【解析】设抛物线的焦点为F,由抛物线的定义知 ,即 ,解得 .
故选:C.
【点晴】本题主要考查利用抛物线的定义计算焦半径,考查学生转化与化归思想,是一道容易题.
4.(2020年高考课标Ⅲ卷理科·第5题)设 为坐标原点,直线 与抛物线C: 交
于 , 两点,若 ,则 的焦点坐标为 ( )
A. B. C. D.
【答案】B
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 33解析:因为直线 与抛物线 交于 两点,且 ,
根据抛物线的对称性可以确定 ,所以 ,
代入抛物线方程 ,求得 ,所以其焦点坐标为 ,
故选:B.
【点睛】该题考查的是有关圆锥曲线的问题,涉及到的知识点有直线与抛物线的交点,抛物线的对称
性,点在抛物线上的条件,抛物线的焦点坐标,属于简单题目.
5.(2022年高考全国乙卷数学(理)·第5题)设F为抛物线 的焦点,点A在C上,点 ,
若 ,则 ( )
A.2 B. C.3 D.
【答案】B
解析:由题意得, ,则 ,
即点 到准线 的距离为2,所以点 的横坐标为 ,
不妨设点 在 轴上方,代入得, ,
所以 . 故选:B
6.(2020北京高考·第7题)设抛物线的顶点为 ,焦点为 ,准线为 . 是抛物线上异于 的一点,
过 作 于 ,则线段 的垂直平分线 ( ).
A.经过点 B.经过点
C.平行于直线 D.垂直于直线
【答案】B
【解析】如图所示: .
因为线段 的垂直平分线上的点到 的距离相等,又点 在抛物线上,根据定义可知,
,所以线段 的垂直平分线经过点 .故选:B.
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 34二、填空题
1.(2023年全国乙卷理科·第13题)已知点 在抛物线C: 上,则A到C的准线的距离为
______.
【答案】
解析:由题意可得: ,则 ,抛物线的方程为 ,
准线方程为 ,点 到 的准线的距离为 .
故答案为: .
2.(2021年新高考Ⅰ卷·第14题)已知 为坐标原点,抛物线 : ( )的焦点为 , 为
上一点, 与 轴垂直, 为 轴上一点,且 ,若 ,则 的准线方程为______.
【答案】
解析:不妨设
因为 ,所以 的准线方程为 ,故答案为 .
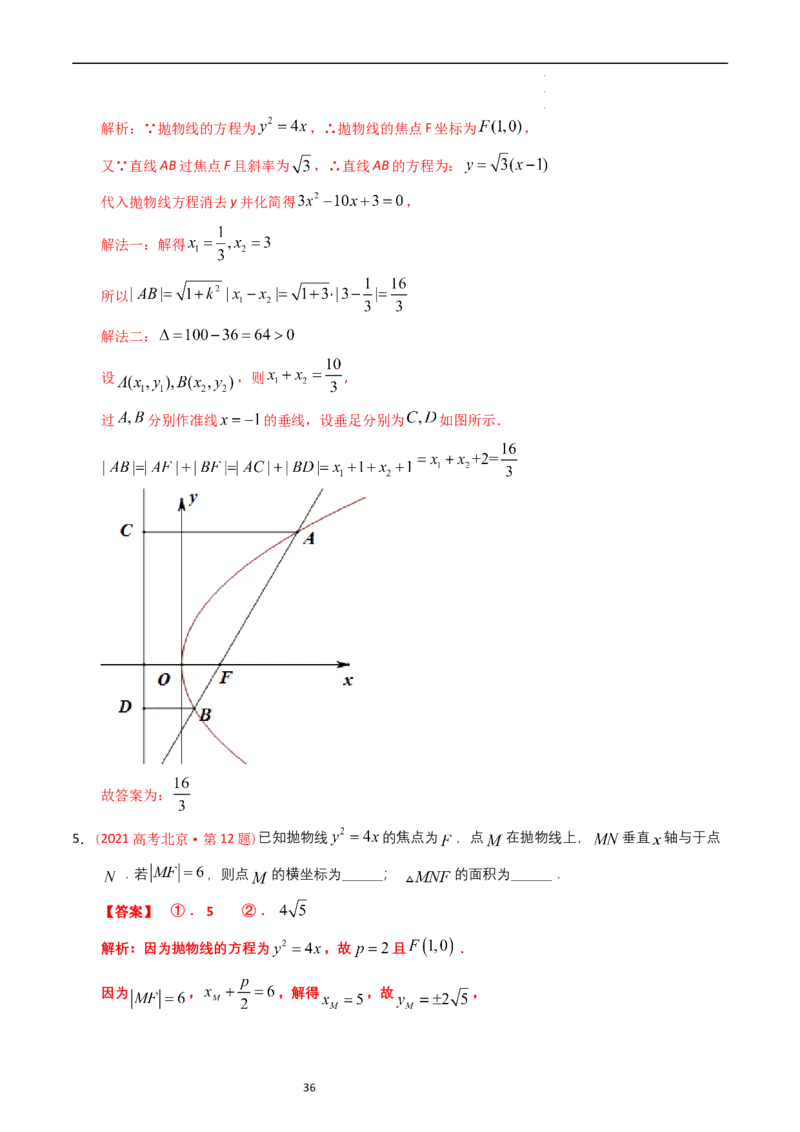
3.(2020年新高考全国Ⅰ卷(山东)·第13题)斜率为 的直线过抛物线C:y2=4x的焦点,且与C交于
A,B两点,则 =________.
【答案】
解析:∵抛物线的方程为 ,∴抛物线 的焦点F坐标为 ,
又∵直线AB过焦点F且斜率为 ,∴直线AB的方程为:
代入抛物线方程消去y并化简得 ,
解得 ,所以
4.(2020年新高考全国卷Ⅱ数学(海南)·第14题)斜率为 直的线过抛物线C:y2=4x的焦点,且与C交
于A,B两点,则 =________.
【答案】
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 35解析:∵抛物线的方程为 ,∴抛物线的焦点F坐标为 ,
又∵直线AB过焦点F且斜率为 ,∴直线AB的方程为:
代入抛物线方程消去y并化简得 ,
解法一:解得
所以
解法二:
设 ,则 ,
过 分别作准线 的垂线,设垂足分别为 如图所示.
故答案为:
5.(2021高考北京·第12题)已知抛物线 的焦点为 ,点 在抛物线上, 垂直 轴与于点
.若 ,则点 的横坐标为_______; 的面积为_______.
【答案】 ①. 5 ②.
解析:因为抛物线的方程为 ,故 且 .
因为 , ,解得 ,故 ,
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 36所以 ,
故答案为:5; .
6.(2019·上海·第9题)过 的焦点 并垂直于 轴的直线分别与 交于 , 在
上方, 为抛物线上一点, ,则 ______.
【答案】3
【解析】依题意求得: , ,设M坐标
有: ,代入 有:
即: .
本题主要考查平面向量、抛物线.
【点评】
7.(2018年高考数学课标Ⅲ卷(理)·第16题)已知点 和抛物线 ,过 的焦点且斜率
为 的直线与 交于 两点,若 ,则 .
【答案】
解析:法一:抛物线 的焦点坐标为 ,可设直线 ,
联立方程 ,消去 并整理可得
所以 ,由点 在抛物线上,可得 ,
所以 ,
由 ,可得 ,所以
所以
即
所以 即 ,解得
故所求直线 的斜率 .
法二:抛物线 的焦点 ,准线方程为
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 37由依题意可知以 为直径的圆与准线相切于点 ,故线段 中点的纵坐标为
设直线 ,
联立方程 ,消去 并整理可得
则有 ,解得
故所求直线 的斜率 .
考点 05 圆锥曲线的综合问题
1.(2023年全国甲卷理科·第8题)已知双曲线 的离心率为 ,C的一条渐
近线与圆 交于A.B两点,则 ( )
A. B. C. D.
【答案】D
解析:由 ,则 ,
解得 ,
所以双曲线的一条渐近线不妨取 ,
则圆心 到渐近线的距离 ,
所以弦长 .
故选:D
2.(2021年高考浙江卷·第9题)已知 ,函数 .若
成等比数列,则平面上点 的轨迹是 ( )
A.直线和圆 B.直线和椭圆 C.直线和双曲线 D.直线和抛物线
【答案】C
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 38解析:由题意得 ,即 ,
对其进行整理变形:
,
, ,
,所以 或 ,其中 为双曲线, 为直
线,故选C.
3.(2019·天津·理·第 5 题)已知抛物线 的焦点为 ,准线为 ,若 与双曲线
的两条渐近线分别交于点 和点 ,且 ( 为原点),则双
曲线的离心率为 ( )
A. B. C. D.
【答案】D
解析: , , ,所以双曲线的两条渐近线方程
为
,所以 ,则双曲线的离心率 .
4.(2019·北京·理·第8题)数学中有许多形状优美、寓意美好的曲线,曲线C: 就
是其中之一(如图).给出下列三个结论:
①曲线C恰好经过6个整点(即横、纵坐标均为整数的点);
②曲线C上任意一点到原点的距离都不超过 ;
③曲线C所围成的“心形”区域的面积小于3.
其中,所有正确结论的序号是 ( )
A.① B.② C.①② D.①②③
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 39【答案】C
【解析】由 得, , ,
所以 可为的整数有0,-1,1,从而曲线 恰好经过(0,1),(0,-1),(1,
0),(1,1), (-1,0),(-1,1)六个整点,结论①正确;
由 得, ,解得 ,所以曲线 上任意一点到原点的
距离都不超过 ,结论②正确;
如图所示,易知 ,四边形 的面积
,
很明显“心形”区域的面积大于 ,即“心形”区域的面积大于3,说法③错误.故选C.
二 填空题:
1.(2023年天津卷·第12题)过原点的一条直线与圆 相切,交曲线
于点 ,若 ,则 的值为_________.
【答案】
解析:易知圆 和曲线 关于 轴对称,不妨设切线方程为 , ,
所以 ,解得: ,由 解得: 或 ,
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 40所以 ,解得: .
当 时,同理可得.
故答案为: .
2.(2023·全国·乙卷)已知点 在抛物线C: 上,则A到C的准线的距离为 .
【分析】由题意首先求得抛物线的标准方程,然后由抛物线方程可得抛物线的准线方程为 ,最后利
用点的坐标和准线方程计算点 到 的准线的距离即可.
【详解】由题意可得: ,则 ,抛物线的方程为 ,
准线方程为 ,点 到 的准线的距离为 .
故答案为: .
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司 41