文档内容
哈师大附中 2021 级高三第二次调研考试
数学试题
(满分150分,考试时间120分钟)
一、选择题(前8个小题为单选题,每题只有一个选项,每题5分,满分40分;后4小题为
多选题,每题不只有一个选项,每题5分,满分20分)
1. 已知集合 , ,则 ( ).
A. B.
C. D.
2. 已知 ,那么 的一个充分不必要条件是( ).
.
A B. C. D.
3. ( ).
A. B. C. D.
4. 已知 , , ,则( ).
A. B. C. D.
5. 若正数 满足 ,则 的最小值为( ).
.
A B. C. D.
6. 已知函数 的定义域为 ,其导函数为 ,且 ,则下列关系一定正确的是(
).
A. B.
第1页/共6页
学科网(北京)股份有限公司C. D.
7. 将函数 图像上所有点的横坐标变为原来的2倍,纵坐标不变,得到函数
,函数 在区间 上有且只有两个零点,则 的取值范围为( ).
A. B. C. D.
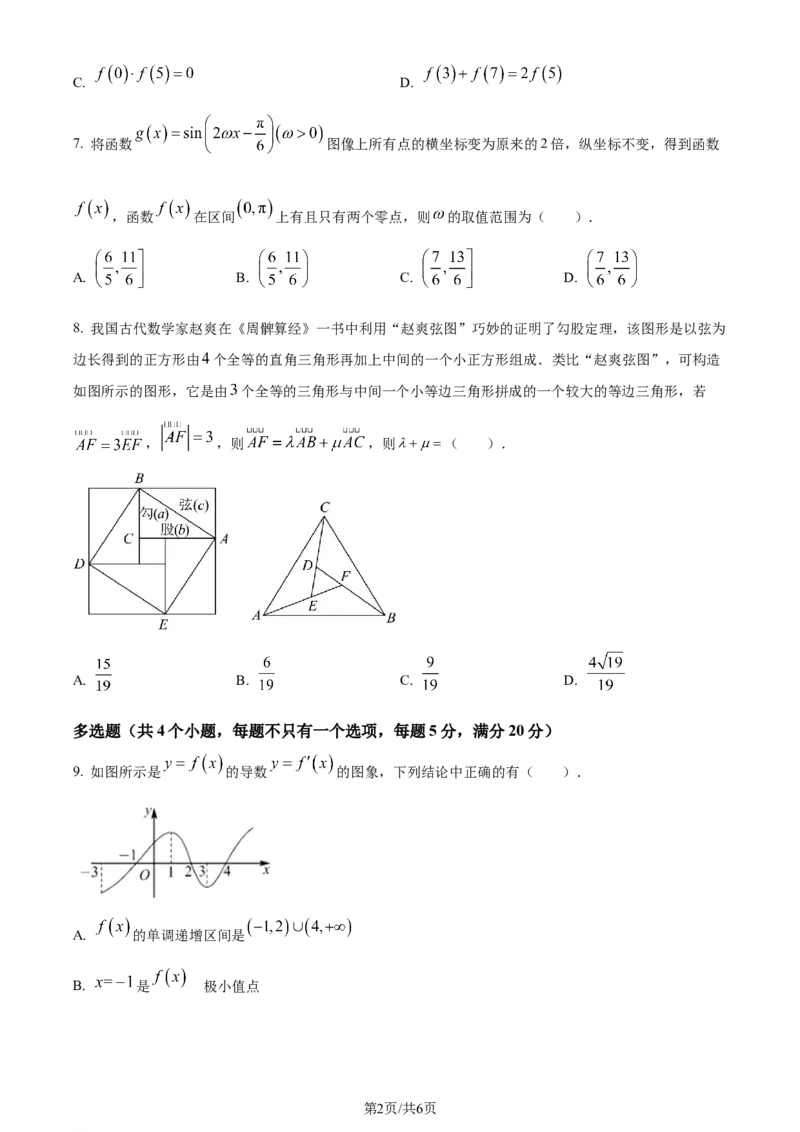
8. 我国古代数学家赵爽在《周髀算经》一书中利用“赵爽弦图”巧妙的证明了勾股定理,该图形是以弦为
边长得到的正方形由 个全等的直角三角形再加上中间的一个小正方形组成.类比“赵爽弦图”,可构造
如图所示的图形,它是由 个全等的三角形与中间一个小等边三角形拼成的一个较大的等边三角形,若
, ,则 ,则 ( ).
A. B. C. D.
多选题(共4个小题,每题不只有一个选项,每题5分,满分20分)
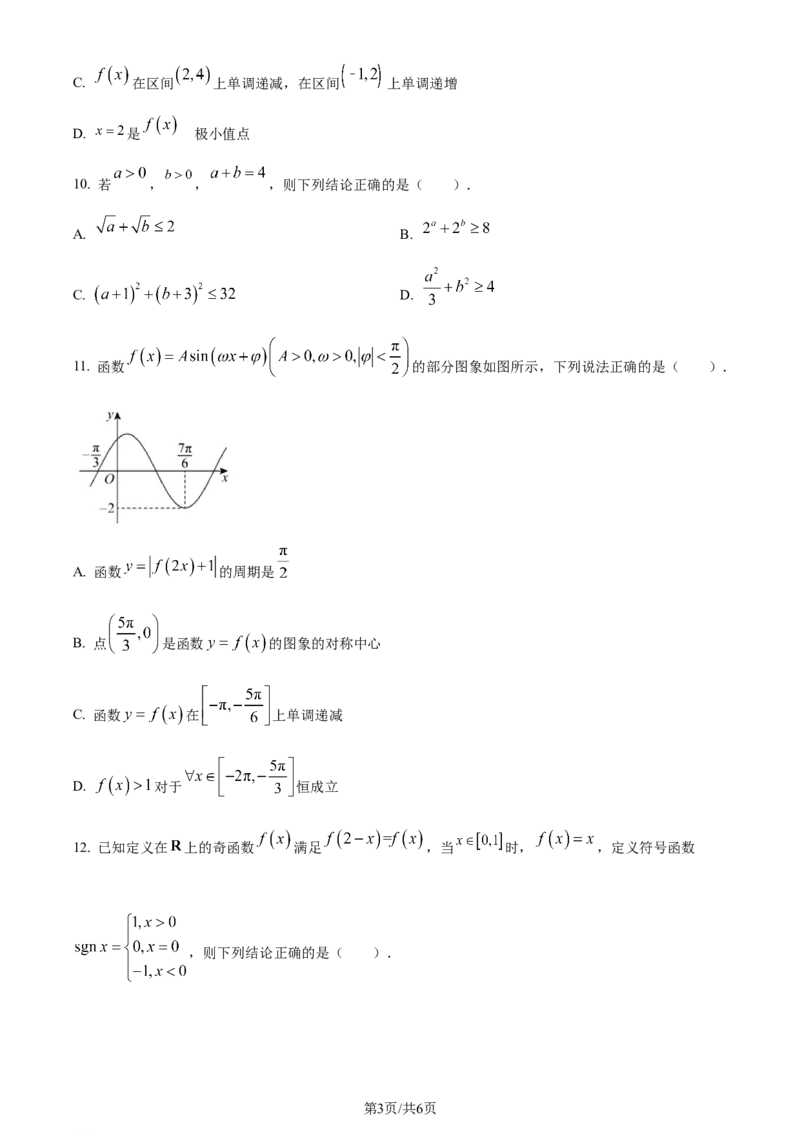
9. 如图所示是 的导数 的图象,下列结论中正确的有( ).
A. 的单调递增区间是
的
B. 是 极小值点
第2页/共6页
学科网(北京)股份有限公司C. 在区间 上单调递减,在区间 上单调递增
的
D. 是 极小值点
10. 若 , , ,则下列结论正确的是( ).
A. B.
C. D.
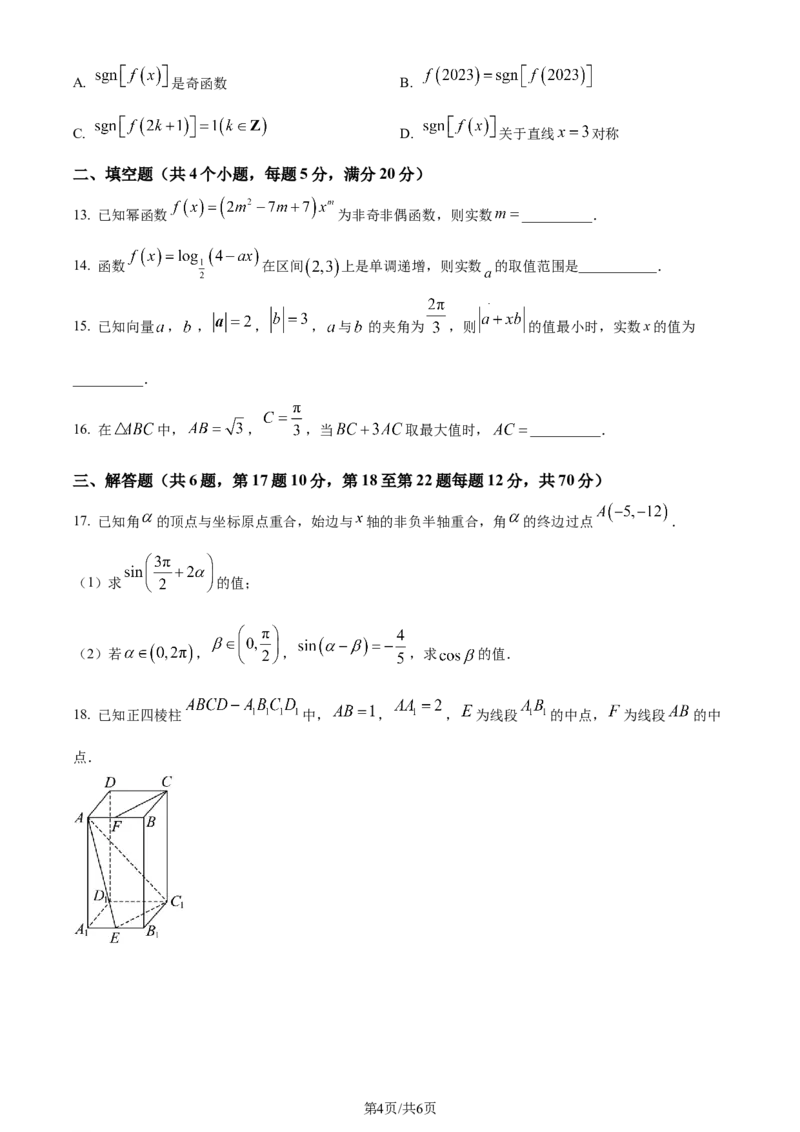
11. 函数 的部分图象如图所示,下列说法正确的是( ).
A. 函数 的周期是
B. 点 是函数 的图象的对称中心
C. 函数 在 上单调递减
D. 对于 恒成立
12. 已知定义在 上的奇函数 满足 ,当 时, ,定义符号函数
,则下列结论正确的是( ).
第3页/共6页
学科网(北京)股份有限公司A. 是奇函数 B.
C. D. 关于直线 对称
二、填空题(共4个小题,每题5分,满分20分)
13. 已知幂函数 为非奇非偶函数,则实数 __________.
14. 函数 在区间 上是单调递增,则实数 的取值范围是___________.
15. 已知向量 , , , , 与 的夹角为 ,则 的值最小时,实数x的值为
__________.
16. 在 中, , ,当 取最大值时, __________.
三、解答题(共6题,第17题10分,第18至第22题每题12分,共70分)
17. 已知角 的顶点与坐标原点重合,始边与 轴的非负半轴重合,角 的终边过点 .
(1)求 的值;
(2)若 , , ,求 的值.
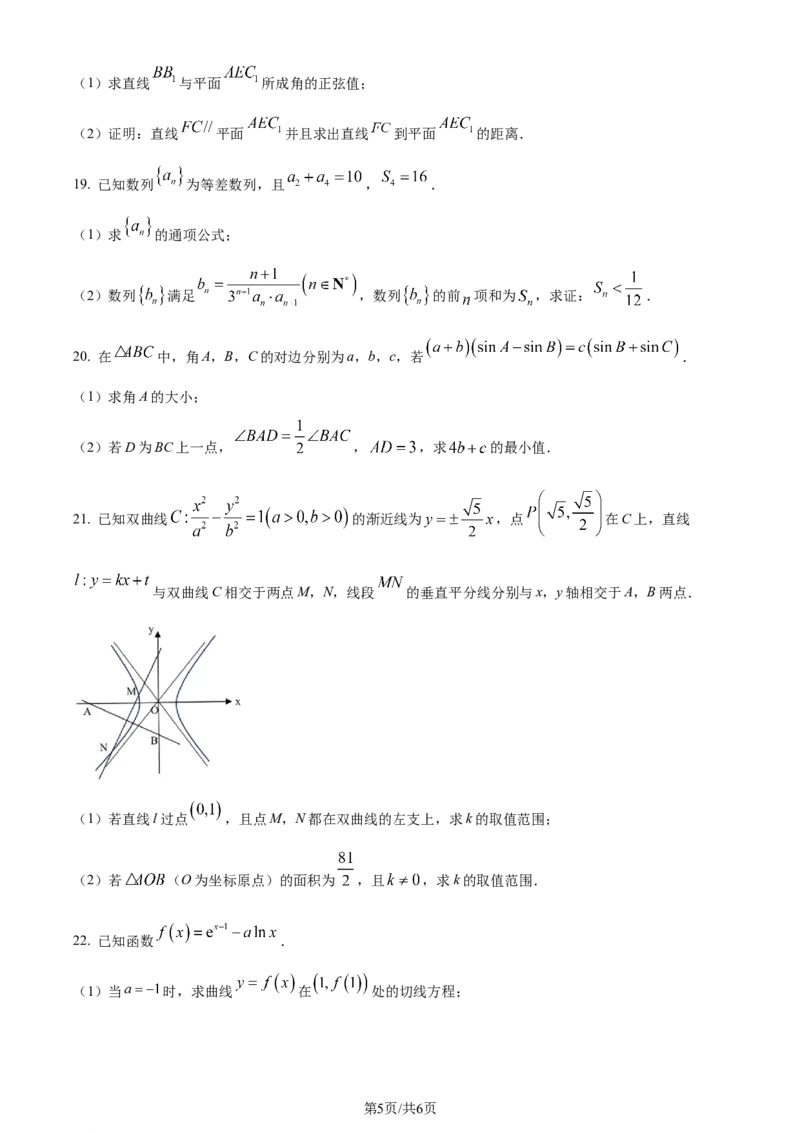
18. 已知正四棱柱 中, , , 为线段 的中点, 为线段 的中
点.
第4页/共6页
学科网(北京)股份有限公司(1)求直线 与平面 所成角的正弦值;
(2)证明:直线 平面 并且求出直线 到平面 的距离.
19. 已知数列 为等差数列,且 , .
(1)求 的通项公式;
(2)数列 满足 ,数列 的前 项和为 ,求证: .
20. 在 中,角A,B,C的对边分别为a,b,c,若 .
(1)求角A的大小;
(2)若D为BC上一点, , ,求 的最小值.
21. 已知双曲线 的渐近线为 ,点 在C上,直线
与双曲线C相交于两点M,N,线段 的垂直平分线分别与x,y轴相交于A,B两点.
(1)若直线l过点 ,且点M,N都在双曲线的左支上,求k的取值范围;
(2)若 (O为坐标原点)的面积为 ,且 ,求k的取值范围.
22. 已知函数 .
(1)当 时,求曲线 在 处的切线方程;
第5页/共6页
学科网(北京)股份有限公司(2)当 ,若不等式 恒成立,求 的取值范围.
第6页/共6页
学科网(北京)股份有限公司