文档内容
五年(2019-2023)年高考真题分项汇编
专题 15 概率与统计(解答题)
概率与统计题型主要包含二项式定理,排列组合,随机抽样,统计与概率等主要考查题型为:
考点01 统计案例及应用
考点02 随机事件分布列
考点03 相关关系与回归分析
考点04 独立性检验
考点05 概率统计的综合应用
考点 01:统计案例及应用
1.(2022高考北京卷)在校运动会上,只有甲、乙、丙三名同学参加铅球比赛,比赛成绩达到 以上
(含 )的同学将获得优秀奖.为预测获得优秀奖的人数及冠军得主,收集了甲、乙、丙以往的比
赛成绩,并整理得到如下数据(单位:m):
甲:9.80,9.70,9.55,9.54,9.48,9.42,9.40,935,9.30,9.25;
乙:9.78,9.56,9.51,9.36,9.32,9.23;
丙:9.85,9.65,9.20,9.16.
假设用频率估计概率,且甲、乙、丙的比赛成绩相互独立.
(1)估计甲在校运动会铅球比赛中获得优秀奖的概率;
(2)设X是甲、乙、丙在校运动会铅球比赛中获得优秀奖的总人数,估计X的数学期望E(X);
(3)在校运动会铅球比赛中,甲、乙、丙谁获得冠军的概率估计值最大?(结论不要求证明)
【答案】
【解析】:(1)由频率估计概率可得
甲获得优秀的概率为0.4,乙获得优秀的概率为0.5,丙获得优秀的概率为0.5,故答案为0.4
(2)设甲获得优秀为事件A ,乙获得优秀为事件A ,丙获得优秀为事件A
1 2 3
,,
,
.
∴X的分布列为
X 0 1 2 3
P
∴
(3)丙夺冠概率估计值最大.
因为铅球比赛无论比赛几次就取最高成绩.比赛一次,丙获得9.85的概率为 ,甲获得9.80的概
率为 ,乙获得9.78的概率为 .并且丙的最高成绩是所有成绩中最高的,比赛次数越多,对丙
越有利.
2.(2023年全国乙卷理科)某厂为比较甲乙两种工艺对橡胶产品伸缩率的处理效应,进行10次配对试验,
每次配对试验选用材质相同的两个橡胶产品,随机地选其中一个用甲工艺处理,另一个用乙工艺处理,
测量处理后的橡胶产品的伸缩率.甲、乙两种工艺处理后的橡胶产品的伸缩率分别记为 ,
.试验结果如下:
试验序号 1 2 3 4 5 6 7 8 9 10
伸缩率 545 533 551 522 575 544 541 568 596 548
伸缩率 536 527 543 530 560 533 522 550 576 536
记 ,记 的样本平均数为 ,样本方差为 .
(1)求 , ;
(2)判断甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率是否有显著提高(如果
,则认为甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高,否则不认为有显著提高)
【答案】(1) , ;
(2)认为甲工艺处理后 的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高.
【解析】:(1) ,
,
,
的值分别为: ,
故
(2)由(1)知: , ,故有 ,
所以认为甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高.
3.(2020年高考课标Ⅰ卷理科·)甲、乙、丙三位同学进行羽毛球比赛,约定赛制如下:累计负两场者被
淘汰;比赛前抽签决定首先比赛的两人,另一人轮空;每场比赛的胜者与轮空者进行下一场比赛,负
者下一场轮空,直至有一人被淘汰;当一人被淘汰后,剩余的两人继续比赛,直至其中一人被淘汰,
另一人最终获胜,比赛结束.经抽签,甲、乙首先比赛,丙轮空.设每场比赛双方获胜的概率都为 ,
(1)求甲连胜四场的概率;
(2)求需要进行第五场比赛的概率;
(3)求丙最终获胜的概率.
【答案】(1) ;(2) ;(3) .
【解析】:”(1)记事件 甲连胜四场,则 ;
(2)记事件 为甲输,事件 为乙输,事件 为丙输,
则四局内结束比赛的概率为
,
所以,需要进行第五场比赛的概率为 ;(3)记事件 为甲输,事件 为乙输,事件 为丙输,
记事件 甲赢,记事件 丙赢,
则甲赢的基本事件包括: 、 、 、
、 、 、 、 ,
所以,甲赢 概率为 .
的
由对称性可知,乙赢的概率和甲赢的概率相等,
所以丙赢的概率为 .
4.(2021年高考全国乙卷理科)某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标
有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:
. .
旧设
9.8 10.3 100 102 9.9 9.8 10.0 10.1 10.2 9.7
备
.
新设
101 10.4 10.1 10.0 10.1 10.3 10.6 10.5 10.4 10.5
备
旧设备和新设备生产产品的该项指标的样本平均数分别记为 和 ,样本方差分别记为 和 .
(1)求 , , , ;
(2)判断新设备生产产品的该项指标的均值较旧设备是否有显著提高(如果 ,则认
为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高).
【答案】(1) ;(2)新设备生产产品的该项指标的均值较旧设备
有显著提高.
【解析】:(1) ,
,
,
.
(2)依题意, , ,,所以新设备生产产品的该项指标的均值较旧设备有显著提高.
5.(2021年新高考Ⅰ卷)某学校组织“一带一路”知识竞赛,有A,B两类问题,每位参加比赛的同学先在
两类问题中选择一类并从中随机抽取一个问题回答,若回答错误则该同学比赛结束:若回答正确则从
另一类问题中再随机抽取一个问题回答,无论回答正确与否,该同学比赛结束.A类问题中的每个问
题回答正确得20分,否则得0分:B类问题中的每个问题回答正确得80分,否则得0分,己知小明能
正确回答A类问题的概率为0.8,能正确回答B类问题的概率为0.6,且能正确回答问题的概率与回
答次序无关.
(1)若小明先回答A类问题,记 为小明的累计得分,求 的分布列;
(2)为使累计得分 的期望最大,小明应选择先回答哪类问题?并说明理由.
【答案】【解析】:(1)由题可知, 的所有可能取值为 , , .
;
;
.
所以 的分布列为
(2)由(1)知, .
若小明先回答 问题,记 为小明的累计得分,则 的所有可能取值为 , , .
;
;
.
所以 .
因为 ,所以小明应选择先回答 类问题.
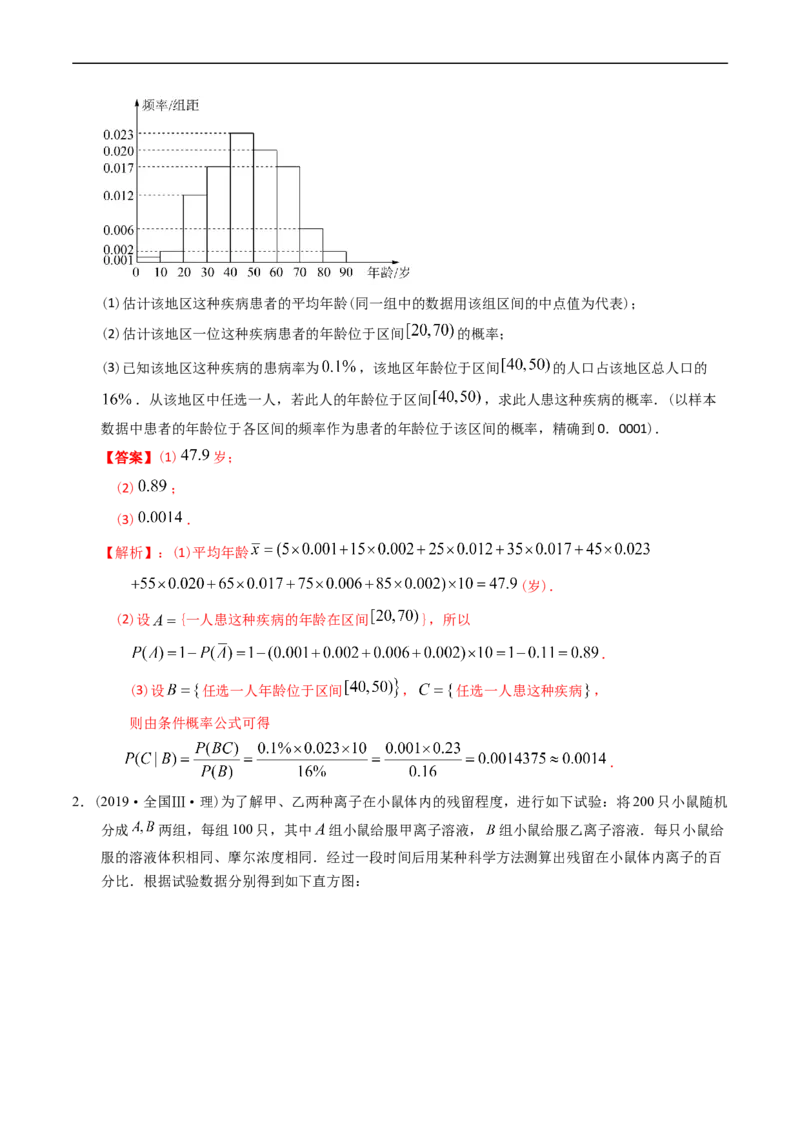
6.(2022新高考全国II卷)在某地区进行流行病学调查,随机调查了100位某种疾病患者的年龄,得到如
下的样本数据的频率分布直方图:(1)估计该地区这种疾病患者的平均年龄(同一组中的数据用该组区间的中点值为代表);
(2)估计该地区一位这种疾病患者的年龄位于区间 的概率;
(3)已知该地区这种疾病的患病率为 ,该地区年龄位于区间 的人口占该地区总人口的
.从该地区中任选一人,若此人的年龄位于区间 ,求此人患这种疾病的概率.(以样本
数据中患者的年龄位于各区间的频率作为患者的年龄位于该区间的概率,精确到0.0001).
【答案】(1) 岁;
(2) ;
(3) .
【解析】:(1)平均年龄
(岁).
(2)设 {一人患这种疾病的年龄在区间 },所以
.
(3)设 任选一人年龄位于区间 , 任选一人患这种疾病 ,
则由条件概率公式可得
.
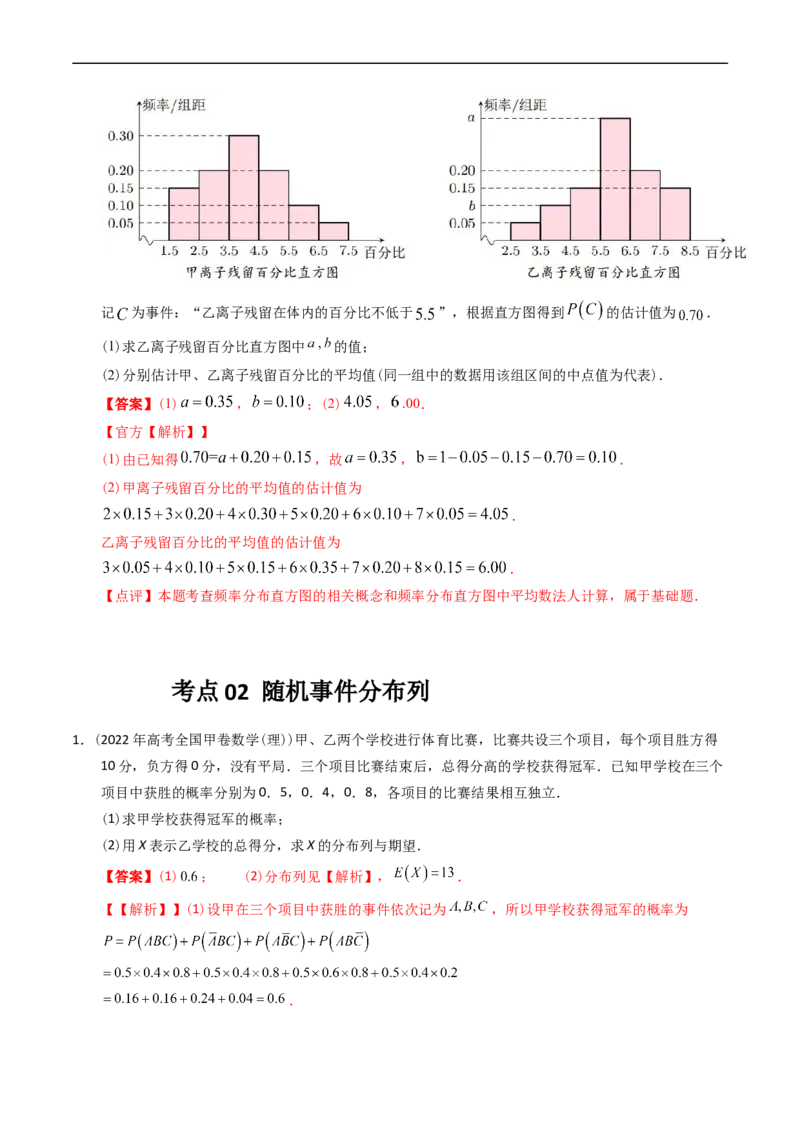
2.(2019·全国Ⅲ·理)为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机
分成 两组,每组100只,其中 组小鼠给服甲离子溶液, 组小鼠给服乙离子溶液.每只小鼠给
服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百
分比.根据试验数据分别得到如下直方图:记 为事件:“乙离子残留在体内的百分比不低于 ”,根据直方图得到 的估计值为 .
(1)求乙离子残留百分比直方图中 的值;
(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
【答案】(1) , ;(2) , .00.
【官方【解析】】
(1)由已知得 ,故 , .
(2)甲离子残留百分比的平均值的估计值为
.
乙离子残留百分比的平均值的估计值为
.
【点评】本题考查频率分布直方图的相关概念和频率分布直方图中平均数法人计算,属于基础题.
考点 02 随机事件分布列
1.(2022年高考全国甲卷数学(理))甲、乙两个学校进行体育比赛,比赛共设三个项目,每个项目胜方得
10分,负方得0分,没有平局.三个项目比赛结束后,总得分高的学校获得冠军.已知甲学校在三个
项目中获胜的概率分别为0.5,0.4,0.8,各项目的比赛结果相互独立.
(1)求甲学校获得冠军的概率;
(2)用X表示乙学校的总得分,求X的分布列与期望.
【答案】(1) ; (2)分布列见【解析】, .
【【解析】】(1)设甲在三个项目中获胜的事件依次记为 ,所以甲学校获得冠军的概率为
.(2)依题可知, 的可能取值为 ,所以,
,
,
,
.
即 的分布列为
0 10 20 30
0.16 0.44 0.34 0.06
期望 .
2.(2021高考北京)在核酸检测中, “k合1” 混采核酸检测是指:先将k个人的样本混合在一起进行1次检
测,如果这k个人都没有感染新冠病毒,则检测结果为阴性,得到每人的检测结果都为阴性,检测结束:
如果这k个人中有人感染新冠病毒,则检测结果为阳性,此时需对每人再进行1次检测,得到每人的检
测结果,检测结束.
现对100人进行核酸检测,假设其中只有2人感染新冠病毒,并假设每次检测结果准确.
(I)将这100人随机分成10组,每组10人,且对每组都采用“10合1”混采核酸检测.
(i)如果感染新冠病毒的2人在同一组,求检测的总次数;
(ii)已知感染新冠病毒的2人分在同一组的概率为 .设X是检测的总次数,求X的
分布列与数学期望E(X).
(II)将这100人随机分成20组,每组5人,且对每组都采用“5合1”混采核酸检测.设Y是检测的总次
数,试判断数学期望E(Y)与(I)中E(X)的大小.(结论不要求证明)
【答案】(1)① 次;②分布列见【解析】;期望为 ;(2) .
【解析】:(1)①对每组进行检测,需要10次;再对结果为阳性的组每个人进行检测,需要10次;
所以总检测次数为20次;
②由题意, 可以取20,30,
, ,
则 的分布列:所以 ;
(2)由题意, 可以取25,30,
两名感染者在同一组的概率为 ,不在同一组的概率为 ,
则 .
3.(2020江苏高考)甲口袋中装有 个黑球和 个白球,乙口袋中装有 个白球.现从甲、乙两口袋中各任
取一个球交换放入另一口袋,重复 次这样的操作,记甲口袋中黑球个数为 ,恰有 个黑球的概率
为 ,恰有 个黑球的概率为 .
(1)求 和 ;
(2)求 与 的递推关系式和 的数学期望 (用 表示).
【答案】(1) (2)
【解析】(1) ,
,
.
(2) ,
,
因此 ,
从而 ,
即 .
又 的分布列为
0 1 2故 .
4.(2019·全国Ⅱ·理) 分制乒乓球比赛,每赢一球得 分,当某局打成 平后,每球交换发球权,
先多得 分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率
为 ,乙发球时甲得分的概率为 ,各球的结果相互独立.在某局双方 平后,甲先发球,
两人又打了 个球该局比赛结束.
求 ;
求事件“ 且甲获胜”的概率.
【答案】 ; .
【解析】 就是 平后,两人又打了 个球该局比赛结束,则这 个球均由甲得分,或者
均由乙得分.因此 .
且甲获胜,就是 平后,两人又打了 个球该局比赛结束,且这 个球的得分情况为:
前两球是甲、乙各得 分,后两球均为甲得分.
因此所求概率为
.
【解析】:
由题意可知,PX 2
所包含的事件为“甲连赢两球或乙连赢两球”,
所以
P( X =2) =0.5�0.4�0.5 0.6 0.5
.
由题意可知, 包含的事件为“前两球甲乙各得 分,后两球均为甲得分”
所以
P( X =4) =0.5创0.6 0.5创0.4+0.5 0.4创0.5 0.4=0.1
.
5.(2019·天津·理·)设甲、乙两位同学上学期间,每天7:30之前到校的概率均为 .假定甲、乙两
位同学到校情况互不影响,且任一同学每天到校情况相互独立.
(Ⅰ)用 表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量 的分布列和数学期望;
(Ⅱ)设 为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的
天数恰好多2”,求事件 发生的概率.
【答案】本小题主要考查离散型随机变量的分布列与数学期望,互斥事件和相互独立事件的概率计算
公式等基础知识.考查运用概率知识解决简单实际问题的能力.满分13分.
(Ⅰ)解:因为甲同学上学期间的三天中到校情况相互独立,且每天 7:30之前到校的概率均为 ,故,从而 .
所以,随机变量 的分布列为
0 1 2 3
随机变量 的数学期望 .
(Ⅱ)解:设乙同学上学期间的三天中7:30之前到校的天数为 ,则 ,
且 .由题意知事件 与 互斥,
且事件 与 ,事件 与 均相互独立,从而由(Ⅰ)知
.
考点 03 相关关系与回归分析
1.(2022年高考全国乙卷数学(理))某地经过多年的环境治理,已将荒山改造成了绿水青山.为估计一林
区某种树木的总材积量,随机选取了10棵这种树木,测量每棵树的根部横截面积(单位: )和材积量(单
位: ),得到如下数据:
样
本 总
1 2 3 4 5 6 7 8 9 10
号 和
i
根
部
横 0. 0. 0. 0. 0. 0. 0. 0. 0.
.
截 0 0 0 0 008 0 0 0 0 0 0.6
面
4 6 4 8 5 5 7 7 6
积
材 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
3.9
积 2 4 2 5 5 3 3 4 4 4量
5 0 2 4 1 4 6 6 2 0
并计算得 .
(1)估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量;
(2)求该林区这种树木的根部横截面积与材积量的样本相关系数(精确到0.01);
(3)现测量了该林区所有这种树木的根部横截面积,并得到所有这种树木的根部横截面积总和为
.已知树木的材积量与其根部横截面积近似成正比.利用以上数据给出该林区这种树木的总材
积量的估计值.
附:相关系数 .
【答案】(1) ;
(2)
(3)
【解析】:【小问1详解】
样本中10棵这种树木的根部横截面积的平均值
样本中10棵这种树木的材积量的平均值
据此可估计该林区这种树木平均一棵的根部横截面积为 ,
平均一棵的材积量为
【小问2详解】
则
【小问3详解】
设该林区这种树木的总材积量的估计值为 ,又已知树木的材积量与其根部横截面积近似成正比,
可得 ,解之得 .则该林区这种树木的总材积量估计为
2.(2020年高考课标Ⅱ卷理科)某沙漠地区经过治理,生态系统得到很大改善,野生动物数量有所增加.
为调查该地区某种野生动物 的数量,将其分成面积相近的200个地块,从这些地块中用简单随机抽样
的方法抽取20个作为样区,调查得到样本数据(x,y)(i=1,2,…,20),其中x和y分别表示第i个
i i i i
样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得 , ,
, , .
(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平
均数乘以地块数);
(2)求样本(x,y)(i=1,2,…,20)的相关系数(精确到0.01);
i i
(3)根据现有统计资料,各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野
生动物数量更准确的估计,请给出一种你认为更合理的抽样方法,并说明理由.
附:相关系数r= , ≈1.414.
【答案】(1) ;(2) ;(3)详见【解析】
【解析】:(1)样区野生动物平均数为 ,
地块数为200,该地区这种野生动物的估计值为
(2)样本 (i=1,2,…,20)的相关系数为
(3)由(2)知各样区的这种野生动物的数量与植物覆盖面积有很强的正相关性,
由于各地块间植物覆盖面积差异很大,从俄各地块间这种野生动物的数量差异很大,
采用分层抽样的方法较好地保持了样本结构与总体结构得以执行,提高了样本的代表性,
从而可以获得该地区这种野生动物数量更准确的估计.
考点 04 独立性检验1.(2023年全国甲卷理科·)一项试验旨在研究臭氧效应.实验方案如下:选40只小白鼠,随机地将其中
20只分配到实验组,另外20只分配到对照组,实验组的小白鼠饲养在高浓度臭氧环境,对照组的小
白鼠饲养在正常环境,一段时间后统计每只小白鼠体重的增加量(单位:g).
(1)设 表示指定的两只小白鼠中分配到对照组的只数,求 的分布列和数学期望;
(2)实验结果如下:
对照组的小白鼠体重的增加量从小到大排序为:
15.2 18.8 20.2 21.3 22.5 23.2 25.8 26.5 27.5 30.1
32.6 34.3 34.8 35.6 35.6 35.8 36.2 37.3 40.5 43.2
对照组的小白鼠体重的增加量从小到大排序为:
7.8 9.2 11.4 12.4 13.2 15.5 16.5 18.0 18.8 19.2
19.8 20.2 21.6 22.8 23.6 23.9 25.1 28.2 32.3 36.5
(i)求40只小鼠体重的增加量的中位数m,再分别统计两样本中小于m与不小于的数据的个数,完成
如下列联表:
对照组
实验组
(ii)根据(i)中的列联表,能否有95%的把握认为小白鼠在高浓度臭氧环境中与正常环境中体重的增加
量有差异.
附:
0.100 0.050 0.010
2.706 3.841 6.635
【答案】(1)分布列见【解析】,
(2)(i) ;列联表见【解析】,(ii)能
【解析】:(1)依题意, 的可能取值为 ,
则 , , ,
所以 的分布列为:故 .
(2)(i)依题意,可知这40只小白鼠体重增量的中位数是将两组数据合在一起,从小到大排后第20位
与第21位数据的平均数,观察数据可得第20位为 ,第21位数据为 ,
所以 ,
故列联表为:
合计
对照组 6 14 20
实验组 14 6 20
合计 20 20 40
(ii)由(i)可得, ,
所以能有 的把握认为小白鼠在高浓度臭氧环境中与正常环境中体重的增加量有差异.
2.(2021年高考全国甲卷理科)甲、乙两台机床生产同种产品,产品按质量分为一级品和二级品,为了比
较两台机床产品的质量,分别用两台机床各生产了200件产品,产品的质量情况统计如下表:
一级品 二级品 合计
甲机床 150 50 200
乙机床 120 80 200
合计 270 130 400
(1)甲机床、乙机床生产的产品中一级品的频率分别是多少?
(2)能否有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异?
附:
0.050 0.010 0.001
k 3.841 6.635 10.828【答案】(1)75%;60%;
(2)能.
【解析】:(1)甲机床生产的产品中的一级品的频率为 ,
乙机床生产的产品中的一级品的频率为 .
(2) ,
故能有99%的把握认为甲机床的产品与乙机床的产品质量有差异.
3.(2020年高考课标Ⅲ卷理科·)某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到
某公园锻炼的人次,整理数据得到下表(单位:天):
锻炼人次
[0,200] (200,400] (400,600]
空气质量等级
1(优) 2 16 25
2(良) 5 10 12
3(轻度污染) 6 7 8
4(中度污染) 7 2 0
(1)分别估计该市一天的空气质量等级为1,2,3,4的概率;
(2)求一天中到该公园锻炼的平均人次的估计值(同一组中的数据用该组区间的中点值为代表);
(3)若某天的空气质量等级为1或2,则称这天“空气质量好”;若某天的空气质量等级为3或4,则
称这天“空气质量不好”.根据所给数据,完成下面的2×2列联表,并根据列联表,判断是否有95%
的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关?
人次≤400 人次>400
空气质量好
空气质量不好
附: ,P(K2≥k) 0.050 0.010 0.001
.
k 3841 6.635 10.828
【答案】(1)该市一天的空气质量等级分别为 、 、 、 的概率分别为 、 、 、 ;
(2) ;(3)有,理由见【解析】.
【解析】:(1)由频数分布表可知,该市一天的空气质量等级为 的概率为 ,等级
为 的概率为 ,等级为 的概率为 ,等级为 的概率为
;
(2)由频数分布表可知,一天中到该公园锻炼的人次的平均数为
(3) 列联表如下:
人次 人次
空气质量不好
空气质量好
,
因此,有 的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关.
【点睛】本题考查利用频数分布表计算频率和平均数,同时也考查了独立性检验的应用,考查数据处
理能力,属于基础题.
4.(2020年新高考全国Ⅰ卷)为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,
随机抽查了 天空气中的 和 浓度(单位: ),得下表:32 18 4
6 8 12
3 7 10
(1)估计事件“该市一天空气中 浓度不超过 ,且 浓度不超过 ”的概率;
(2)根据所给数据,完成下面的 列联表:
(3)根据(2)中 的列联表,判断是否有 的把握认为该市一天空气中 浓度与 浓度有关?
附: ,
0.050 0.010 0.
001
3.841 6.635
10.828
【答案】(1) ;(2)答案见【解析】;(3)有.
【解析】:(1)由表格可知,该市100天中,空气中的 浓度不超过75,且 浓度不超过150
的天数有 天,
所以该市一天中,空气中的 浓度不超过75,且 浓度不超过150的概率为 ;
(2)由所给数据,可得 列联表为:
合计
64 16 8010 10 20
合计 74 26 100
(3)根据 列联表中的数据可得
,
因为根据临界值表可知,有 的把握认为该市一天空气中 浓度与 浓度有关.
5.(2020年新高考全国卷Ⅱ数学)为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调
研,随机抽查了 天空气中的 和 浓度(单位: ),得下表:
(1)估计事件“该市一天空气中 浓度不超过 ,且 浓度不超过 ”的概率;
(2)根据所给数据,完成下面的 列联表:(3)根据(2)中的列联表,判断是否有 的把握认为该市一天空气中 浓度与 浓度有关?
附: ,
【答案】(1) ;(2)答案见【解析】;(3)有.
【解析】:(1)由表格可知,该市100天中,空气中的 浓度不超过75,且 浓度不超过150
的天数有 天,
所以该市一天中,空气中的 浓度不超过75,且 浓度不超过150的概率为 ;
(2)由所给数据,可得 列联表为:
合计
64 16 80
10 10 20
合计 74 26 100
(3)根据 列联表中的数据可得
,
因为根据临界值表可知,有 的把握认为该市一天空气中 浓度与 浓度有关.
考点 05 概率统计综合应用
1.(2023年新高考全国Ι卷)甲、乙两人投篮,每次由其中一人投篮,规则如下:若命中则此人继续投
篮,若末命中则换为对方投篮.无论之前投篮情况如何,甲每次投篮的命中率均为0.6,乙每次投篮的命
中率均为0.8.由抽签确定第1次投篮的人选,第1次投篮的人是甲、乙的概率各为0.5.
(1)求第2次投篮的人是乙的概率;(2)求第 次投篮的人是甲的概率;
(3)已知:若随机变量 服从两点分布,且 ,则 .
记前 次(即从第1次到第 次投篮)中甲投篮的次数为 ,求 .
【答案】(1) (2) (3)
【解析】:(1)记“第 次投篮的人是甲”为事件 ,“第 次投篮的人是乙”为事件 ,
所以,
.
(2)设 ,依题可知, ,则
,
即 ,
构造等比数列 ,
设 ,解得 ,则 ,
又 ,所以 是首项为 ,公比为 的等比数列,
即 .
(3)因为 , ,
所以当 时, ,
故 .
2(2023年新课标全国Ⅱ卷).某研究小组经过研究发现某种疾病的患病者与未患病者的某项医学指标有
明显差异,经过大量调查,得到如下的患病者和未患病者该指标的频率分布直方图:利用该指标制定一个检测标准,需要确定临界值c,将该指标大于c的人判定为阳性,小于或等于c的人判
定为阴性.此检测标准的漏诊率是将患病者判定为阴性的概率,记为 ;误诊率是将未患病者判定为阳
性的概率,记为 .假设数据在组内均匀分布,以事件发生的频率作为相应事件发生的概率.
(1)当漏诊率 %时,求临界值c和误诊率 ;
(2)设函数 ,当 时,求 的【解析】式,并求 在区间 的最小值.
【答案】(1) , ;
(2) ,最小值为 .
【分析】(1)根据题意由第一个图可先求出 ,再根据第二个图求出 的矩形面积即可解出;
(2)根据题意确定分段点 ,即可得出 的【解析】式,再根据分段函数的最值求法即可解出.
【解析】:(1)依题可知,左边图形第一个小矩形的面积为 ,所以 ,
所以 ,解得: ,
.
(2)当 时,
;
当 时,
,
故 ,
所以 在区间 的最小值为 .3.(2021年新高考全国Ⅱ卷·第21题)一种微生物群体可以经过自身繁殖不断生存下来,设一个这种微生
物为第0代,经过一次繁殖后为第1代,再经过一次繁殖后为第2代……,该微生物每代繁殖的个数是相
互独立的且有相同的分布列,设X表示1个微生物个体繁殖下一代的个数, .
(1)已知 ,求 ;
(2)设p表示该种微生物经过多代繁殖后临近灭绝 的概率,p是关于x的方程:
的一个最小正实根,求证:当 时, ,当 时, ;
(3)根据你的理解说明(2)问结论的实际含义.
【答案】【解析】:(1) .
(2)设 ,
因为 ,故 ,
若 ,则 ,故 . ,
因为 , ,故 有两个不同零点 ,且
,且 时, ; 时, ;
故 在 , 上为增函数,在 上为减函数,若 ,因为 在 为
增函数且 ,而当 时,因为 在 上为减函数,故 ,
故 为 的一个最小正实根,
若 ,因为 且在 上为减函数,故1为 的一个最小正实根,
综上,若 ,则 .
若 ,则 ,故 .此时 ,
,故 有两个不同零点 ,且 ,
且 时, ; 时, ;故 在 , 上
为增函数,在 上为减函数,而 ,故 ,又 ,故 在 存
在一个零点 ,且 .所以 为 的一个最小正实根,此时 ,故当
时, .
(3)意义:每一个该种微生物繁殖后代的平均数不超过1,则若干代必然灭绝,若繁殖后代的平均数超
过1,则若干代后被灭绝的概率小于1.
4.(2019·全国Ⅰ·理·第21题)为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,
为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机
选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈
的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述
问题,约定,对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得 1分,乙药得-1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得-1分;若都治愈或都
未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为 和 ,一轮试验中甲药的得分记为X.
(1)求X的分布列;
(2)若甲药、乙药在试验开始时都赋予4分, 表示“甲药的累计得分为 时,最终认为
甲药比乙药更有效”的概率,则 ( ),
其中 , , .假设 , .
(i)证明: 为等比数列;
(ii)求 ,并根据 的值解释这种试验方案的合理性.
【答案】【解析】(1)解:X的所有可能取值为 ,
.
所以 的分布列为
X 0 1
P
(2)(i)由(1)得 .
因此 ,故 ,即 .
又因为 ,所以 为公比为4,首项为 的等比数列.
(ii)由(i)可得
.
由 于 , 故 , 所 以
.
表示最终认为甲药更有效的概率,由计算结果可以看出,在甲药治愈率为0.5,乙药治愈率为0.8时,
认为甲药更有效的概率为 ,此时得出错误结论的概率非常小,说明这种试验方案合